沪科版八年级上册 12.5一次函数复习 课件(共20张PPT)
文档属性
| 名称 | 沪科版八年级上册 12.5一次函数复习 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 18:44:28 | ||
图片预览






文档简介
(共20张PPT)
一次函数小结与复习
知识点回顾与强化
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,⑵比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
知识点回顾与强化
(1)一次函数的解析式是 ,图象是 .
(2) 时,y随x的增大而增大, 时, y随x的增大而减大.
(3)如何求直线与两坐标轴的交点A.B坐标
(4)k,b符号与图象的关系.
Y=kx+b(k≠0)
一条直线
K>0
K<0
X=0时,y=b,即直线与x轴交点坐标为A(0,b)
Y=0时,X= ,即直线与Y轴交点坐标为( , 0)
应用探究
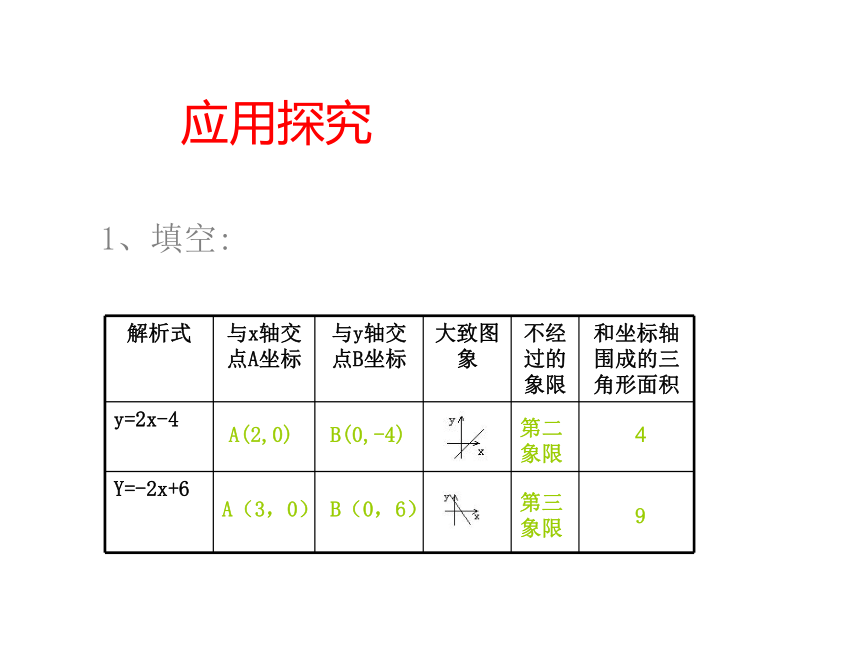
1、填空:
解析式 与x轴交点A坐标 与y轴交点B坐标 大致图象 不经过的象限 和坐标轴围成的三角形面积
y=2x-4
Y=-2x+6
A(2,0)
B(0,-4)
第二象限
4
A(3,0)
B(0,6)
第三象限
9
应用探究
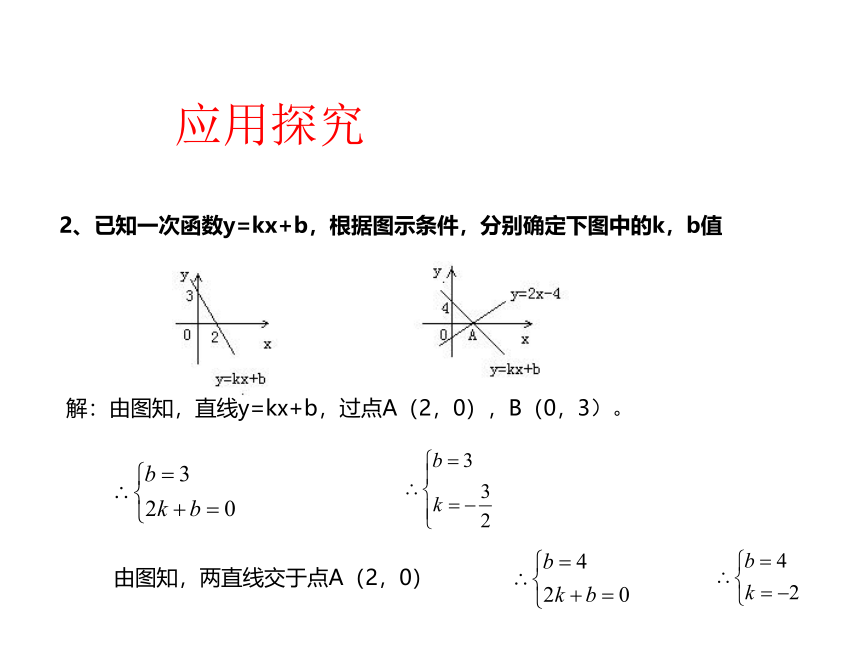
2、已知一次函数y=kx+b,根据图示条件,分别确定下图中的k,b值
解:由图知,直线y=kx+b,过点A(2,0),B(0,3)。
由图知,两直线交于点A(2,0)
3、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。
解:一次函数当x=1时,y=5。且它的图象与x轴交点
是(6,0)。由题意得
∴一次函数的解析式为 y= - x+6。
应用探究
4、y+b与x+a (a、 b是常数)成正比例,当x=3时,y=5, x=2时,y=2 ,当求y与x之间的函数关系式。
∴ y+b=k(x+a) 即 y=kx+ka-b
解:∵ y+b与x+a (a、 b是常数)成正比例
∴ 5=3k+ka-b
2=2k+ka-b
解得:k=3 ka-b=-4
∴ 函数关系式为 y=3x-4
本题的关健是把ka-b看成一个整体,并不是要求a和b
应用探究
知识拓展 一次函数与二元一次方程
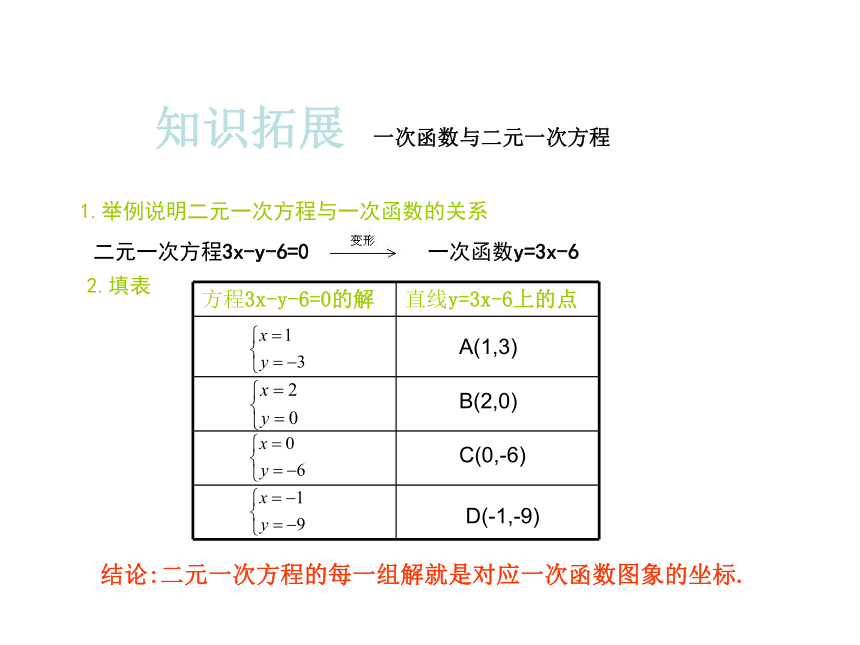
1.举例说明二元一次方程与一次函数的关系
二元一次方程3x-y-6=0 一次函数y=3x-6
2.填表
方程3x-y-6=0的解 直线y=3x-6上的点
A(1,3)
B(2,0)
C(0,-6)
D(-1,-9)
结论:二元一次方程的每一组解就是对应一次函数图象的坐标.
知识拓展 一次函数与二元一次方程组
二元一次方程组与一次函数的关系探讨
在同一坐标系中作y=-3x+1和y=2x-4的图象,并指出交点坐标.
得出的结论是什么
二元一次方程组的解就是对应两个一次函数图象的交点坐标.
若求两直线交点坐标,该如何求
解方程组
一元次方程,一元一次不等式与一次函数的关系探讨
X取何值时y>0,y=0,y<0
结论:一元次方程(组),一元一次不等式的解实质是一次函数图象上的点的坐标,这就是数与形的结合.我们不仅可以用代数方法算出一元次方程(组),一元一次不等式的解还可以从一次函数的中图象看出.
知识拓展 一次函数与不等式
如图给每个交点标出字母,你能否用多种方法求得四边形OABC的面积
(1,1.5)
方法一:利用大三角形减小三角形
方法二:把四边形分割成梯形和三角形
方法三:把四边形分割成两个小三角形
知识拓展 三角形的面积
知识拓展 学生练讲
1.若直线y=ax+7经过一次函数y=4-3x和y=2x-1的交点,求a的值.
2.如图所示,求两直线的解析式及图像的交点坐标
3、在直角坐标系中,直线L1经过点(2,3)和(-1,-3),直线L2经过原点,且与直线L1交于点(-2,a).
(1)求a的值.
(2)(-2,a)可看成怎样的二元一次方程组的解
(3)设交点为P,直线L1与y轴交于点A,你能求出△APO的面积吗
知识拓展 学生练讲
4、如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).
知识拓展 学生练讲
例1、某人从A城出发,前往离A城30千米的B城.现在有三种车供他选择:(1)自行车,其速度为15千米/小时;(2)三轮车,其速度为10千米/小时;(3)摩托车,其速度为40千米/小时.
(1)用哪种车能使他从A城到达B城不超过2小时,请说明理由.
(2)设此人在行进途中离B城的路程为s千米,行进时间为t小时.就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围)。
解:(1)选择用自行车或摩托车能使他从A城到B城不超过2 小时。理由如下:
①自行车:30÷15=2(小时) ②三轮车:30÷10=3(小时)>2(小时) ③摩托车:30÷40= (小时)<2(小时)
(2)骑自行车s=30-15t (0≤t≤2) 或骑摩托车s=30-40t (0≤t ≤ )
知识拓展 典 例 解 析
例2、汽车行驶中,司机从判断出现了紧急情况到进行刹车时,这一段汽车走过的路程称为刹车反应距离.某研究机构收集了有关刹车反应距离的数据如下表:
表中x为汽车行驶速度(英里/小时),y为刹车反应距离(英尺);m,n为丢失的数据.由表中给出的有序实数对,在指教坐标系中对应的点如图所示.
(1)请用平滑曲线顺次连结图中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由.
(2)请利用估计所得到的函数关系,求出表中m,n的植.
x 20 25 30 35 40 45 50 55 60 65 70 75 80
y 22 m 33 38.5 44 50 55 n 66 71 77 82.5 88
解:(1)连线. y与x的关系最近似于正比例(或一次)函数.这是因为图象上除(45,50)和(65,71)两点略微偏离直线外,其他各点均在同一直线上;
(2)设直线为y=kx+b(k≠ 0),将(20,22)、(30,33)分别代入,求得k=1.1,b=0, ∴y=1.1x.
当x=25时,y=27.5, m=27.5
当x=55时,y=60.5, n=60.5.
知识拓展 典 例 解 析
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是
960 元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例3、为美化深圳市景,园林部门决定利用现有的 3 490 盆甲种花卉和 2 950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
知识拓展 典 例 解 析
知识拓展 典 例 解 析
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
方案①需成本:31×800+19×960=43 040(元);
方案②需成本:32×800+18×960=42 880(元);
方案③需成本:33×800+17×960=42 720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48 000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值为
33×800+17×960=42 720(元).
即最低成本是 42 720 元.
知识拓展 典 例 解 析
小结与归纳
1、知识点
⑴一次函数的基本性质
(2)待定系数法
(3)一次函数与二元一次方程组
(4)一次函数与图形的面积
(5)一次函数与不等式
2 、你认为学习好函数要从几方面入手
一次函数小结与复习
知识点回顾与强化
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,⑵比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
知识点回顾与强化
(1)一次函数的解析式是 ,图象是 .
(2) 时,y随x的增大而增大, 时, y随x的增大而减大.
(3)如何求直线与两坐标轴的交点A.B坐标
(4)k,b符号与图象的关系.
Y=kx+b(k≠0)
一条直线
K>0
K<0
X=0时,y=b,即直线与x轴交点坐标为A(0,b)
Y=0时,X= ,即直线与Y轴交点坐标为( , 0)
应用探究
1、填空:
解析式 与x轴交点A坐标 与y轴交点B坐标 大致图象 不经过的象限 和坐标轴围成的三角形面积
y=2x-4
Y=-2x+6
A(2,0)
B(0,-4)
第二象限
4
A(3,0)
B(0,6)
第三象限
9
应用探究
2、已知一次函数y=kx+b,根据图示条件,分别确定下图中的k,b值
解:由图知,直线y=kx+b,过点A(2,0),B(0,3)。
由图知,两直线交于点A(2,0)
3、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。
解:一次函数当x=1时,y=5。且它的图象与x轴交点
是(6,0)。由题意得
∴一次函数的解析式为 y= - x+6。
应用探究
4、y+b与x+a (a、 b是常数)成正比例,当x=3时,y=5, x=2时,y=2 ,当求y与x之间的函数关系式。
∴ y+b=k(x+a) 即 y=kx+ka-b
解:∵ y+b与x+a (a、 b是常数)成正比例
∴ 5=3k+ka-b
2=2k+ka-b
解得:k=3 ka-b=-4
∴ 函数关系式为 y=3x-4
本题的关健是把ka-b看成一个整体,并不是要求a和b
应用探究
知识拓展 一次函数与二元一次方程
1.举例说明二元一次方程与一次函数的关系
二元一次方程3x-y-6=0 一次函数y=3x-6
2.填表
方程3x-y-6=0的解 直线y=3x-6上的点
A(1,3)
B(2,0)
C(0,-6)
D(-1,-9)
结论:二元一次方程的每一组解就是对应一次函数图象的坐标.
知识拓展 一次函数与二元一次方程组
二元一次方程组与一次函数的关系探讨
在同一坐标系中作y=-3x+1和y=2x-4的图象,并指出交点坐标.
得出的结论是什么
二元一次方程组的解就是对应两个一次函数图象的交点坐标.
若求两直线交点坐标,该如何求
解方程组
一元次方程,一元一次不等式与一次函数的关系探讨
X取何值时y>0,y=0,y<0
结论:一元次方程(组),一元一次不等式的解实质是一次函数图象上的点的坐标,这就是数与形的结合.我们不仅可以用代数方法算出一元次方程(组),一元一次不等式的解还可以从一次函数的中图象看出.
知识拓展 一次函数与不等式
如图给每个交点标出字母,你能否用多种方法求得四边形OABC的面积
(1,1.5)
方法一:利用大三角形减小三角形
方法二:把四边形分割成梯形和三角形
方法三:把四边形分割成两个小三角形
知识拓展 三角形的面积
知识拓展 学生练讲
1.若直线y=ax+7经过一次函数y=4-3x和y=2x-1的交点,求a的值.
2.如图所示,求两直线的解析式及图像的交点坐标
3、在直角坐标系中,直线L1经过点(2,3)和(-1,-3),直线L2经过原点,且与直线L1交于点(-2,a).
(1)求a的值.
(2)(-2,a)可看成怎样的二元一次方程组的解
(3)设交点为P,直线L1与y轴交于点A,你能求出△APO的面积吗
知识拓展 学生练讲
4、如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).
知识拓展 学生练讲
例1、某人从A城出发,前往离A城30千米的B城.现在有三种车供他选择:(1)自行车,其速度为15千米/小时;(2)三轮车,其速度为10千米/小时;(3)摩托车,其速度为40千米/小时.
(1)用哪种车能使他从A城到达B城不超过2小时,请说明理由.
(2)设此人在行进途中离B城的路程为s千米,行进时间为t小时.就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围)。
解:(1)选择用自行车或摩托车能使他从A城到B城不超过2 小时。理由如下:
①自行车:30÷15=2(小时) ②三轮车:30÷10=3(小时)>2(小时) ③摩托车:30÷40= (小时)<2(小时)
(2)骑自行车s=30-15t (0≤t≤2) 或骑摩托车s=30-40t (0≤t ≤ )
知识拓展 典 例 解 析
例2、汽车行驶中,司机从判断出现了紧急情况到进行刹车时,这一段汽车走过的路程称为刹车反应距离.某研究机构收集了有关刹车反应距离的数据如下表:
表中x为汽车行驶速度(英里/小时),y为刹车反应距离(英尺);m,n为丢失的数据.由表中给出的有序实数对,在指教坐标系中对应的点如图所示.
(1)请用平滑曲线顺次连结图中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由.
(2)请利用估计所得到的函数关系,求出表中m,n的植.
x 20 25 30 35 40 45 50 55 60 65 70 75 80
y 22 m 33 38.5 44 50 55 n 66 71 77 82.5 88
解:(1)连线. y与x的关系最近似于正比例(或一次)函数.这是因为图象上除(45,50)和(65,71)两点略微偏离直线外,其他各点均在同一直线上;
(2)设直线为y=kx+b(k≠ 0),将(20,22)、(30,33)分别代入,求得k=1.1,b=0, ∴y=1.1x.
当x=25时,y=27.5, m=27.5
当x=55时,y=60.5, n=60.5.
知识拓展 典 例 解 析
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是
960 元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例3、为美化深圳市景,园林部门决定利用现有的 3 490 盆甲种花卉和 2 950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
知识拓展 典 例 解 析
知识拓展 典 例 解 析
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
方案①需成本:31×800+19×960=43 040(元);
方案②需成本:32×800+18×960=42 880(元);
方案③需成本:33×800+17×960=42 720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48 000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值为
33×800+17×960=42 720(元).
即最低成本是 42 720 元.
知识拓展 典 例 解 析
小结与归纳
1、知识点
⑴一次函数的基本性质
(2)待定系数法
(3)一次函数与二元一次方程组
(4)一次函数与图形的面积
(5)一次函数与不等式
2 、你认为学习好函数要从几方面入手
