沪科版八年级上册 14.2.3三角形全等的判定定理3(SSS) 课件(共21张PPT)
文档属性
| 名称 | 沪科版八年级上册 14.2.3三角形全等的判定定理3(SSS) 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 18:53:00 | ||
图片预览




文档简介
(共21张PPT)
边角边(SAS):
我们学过几种三角形的全等判定方法呢?
角边角(ASA):
两边及其夹角分别相等的两个三角形全等
两角及其夹边分别相等的两个三角形全等
1.经历探索三角形全等条件的过程(即如何用尺规作图:已知三边作三角形),体会利用操作、归纳获得数学结论的过程;
2.掌握全等三角形的判定方法“SSS”,并会运用该方法判断三角形是否全等,为证明线段相等或角相等创造条件;
3.了解三角形的稳定性.
学习重点:运用“SSS”证明两个三角形全等.
学习难点:寻求适当的方法证明三角形全等.
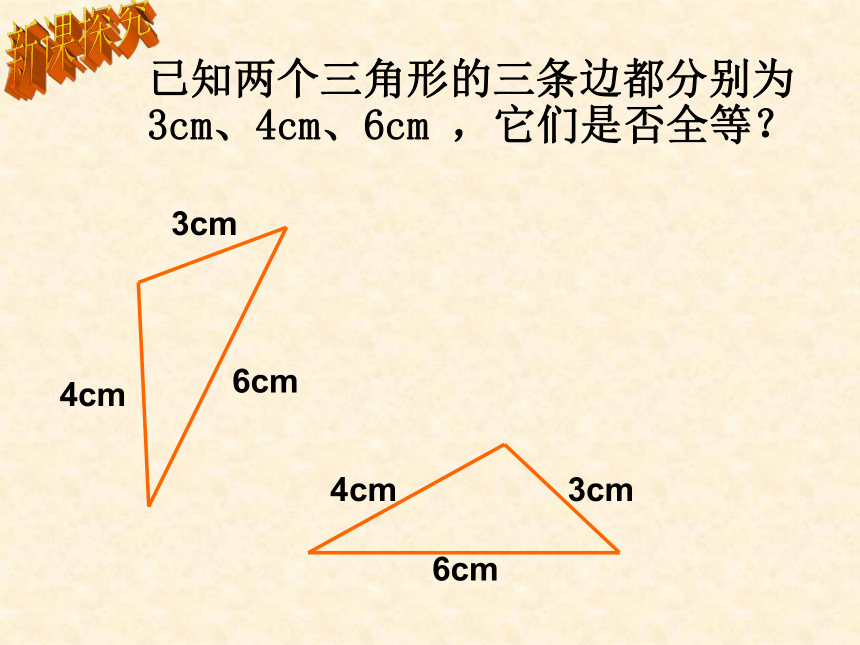
已知两个三角形的三条边都分别为3cm、4cm、6cm ,它们是否全等?
3cm
4cm
6cm
4cm
6cm
3cm
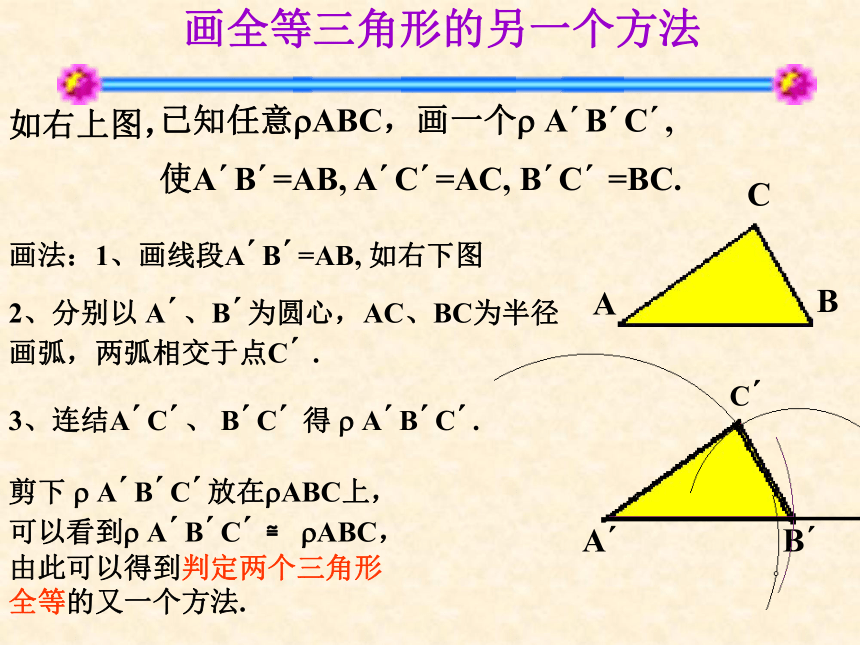
画全等三角形的另一个方法
如右上图,
画法:1、画线段A B =AB, 如右下图
2、分别以 A 、B 为圆心,AC、BC为半径画弧,两弧相交于点C .
3、连结A C 、 B C 得 A B C .
剪下 A B C 放在 ABC上,可以看到 A B C ≌ ABC,由此可以得到判定两个三角形全等的又一个方法.
A
B
C
A
B
C
已知任意 ABC,画一个 A B C ,
使A B =AB, A C =AC, B C =BC.
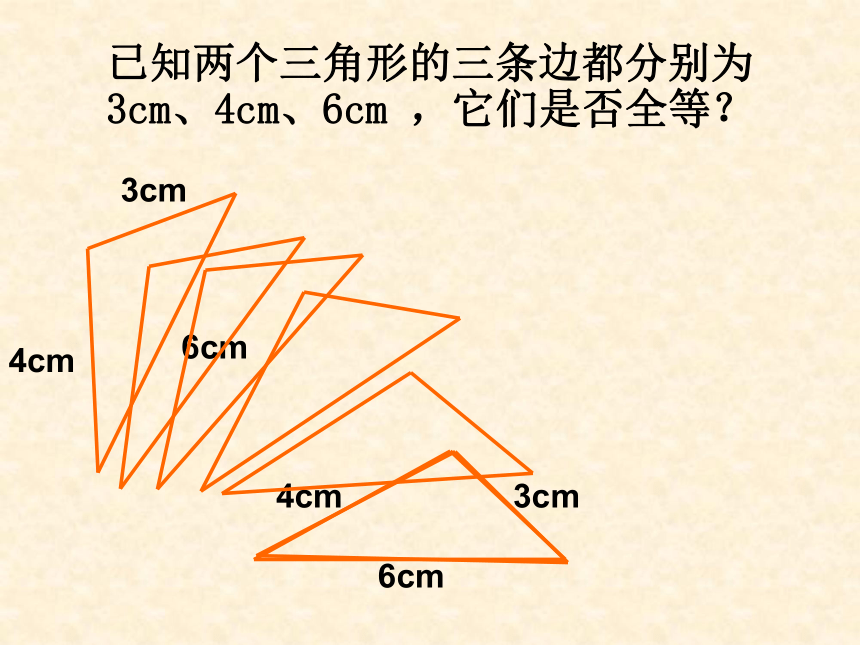
已知两个三角形的三条边都分别为3cm、4cm、6cm ,它们是否全等?
3cm
4cm
6cm
4cm
6cm
3cm
判定两个三角形全等的方法:
三边分别相等的两个三角形全等,简记为“边边边”或“SSS”
A
B
C
A
B
C
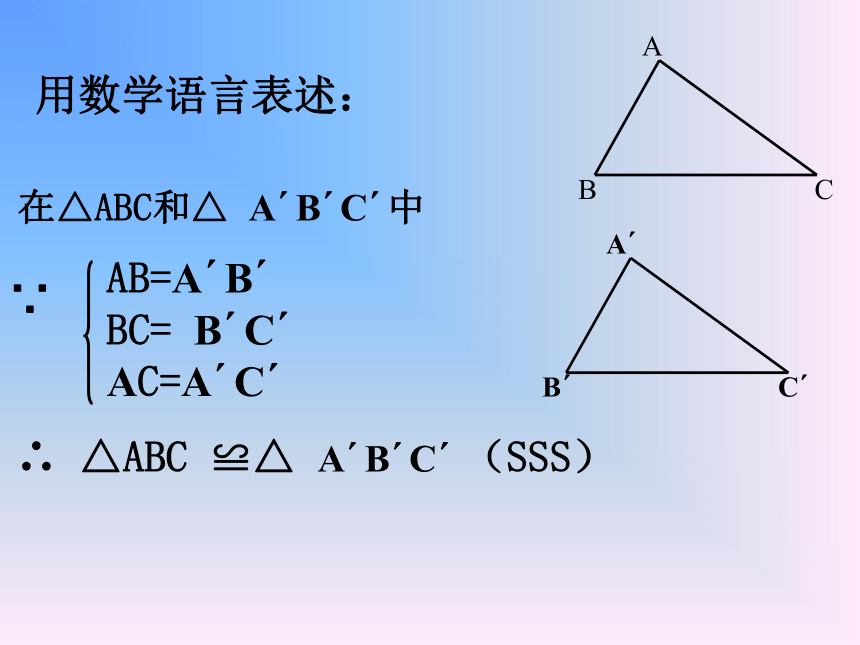
用数学语言表述:
在△ABC和△ A B C 中
∴ △ABC ≌△ A B C (SSS)
AB=A B BC= B C AC=A C
∵
思考:你能用“边边边”解释 三角形具有稳定性吗?
注: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。
1、下面四个三角形中,全等的是( )和( )
4
①
6
8
4
③
6
8
5
7
7
②
7
7
4
④
①
③
2.下列说法中,正确的有( )个
①周长相等的两个三角形全等,②面积相等的两个三角形全等,③有三个角对应相等的两个三角形全等,④有三边对应相等的两个三角形全等
A、1 B、2 C、3 D、4
A
例5. 如下图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF
证明:∵BE=CF (已知)
∴BE+EC=CF+CE(等式性质)
即BC=EF
在△ABC和△DEF中
AB=DE (已知)
AC=DF (已知)
BC=EF(已证)
∴△ABC≌△DEF (SSS)
∴∠B=∠DEF, ∠ACB=∠F(全等三角形的对应角相等)
∴AB ∥DE,AC∥DF(同位角相等两直线平行)
∵
A
F
B
E
C
D
C
O
A
B
如图,OA=OB,AC=BC. 求证:∠AOC=∠BOC.
∵
OA=OB
AC=BC
OC=OC
(公共边)
(已知)
(已知)
∴△ AOC ≌△ BOC (SSS)
在△ AOC 和△ BOC中
证明:
练 习 1
∴∠AOC=∠BOC
(全等三角形的对应角相等)
练 习 2
已知:如图,AB=CD,AD=CB.
求证: ∠A= ∠C.
证明:
连接BD
在 ABD 和 CDB中
∵
AB = CD (已知)
AD = CB (已知)
BD = DB (公共边)
∴ ABD ≌ CDB (SSS)
∴∠A = ∠C (全等三角形的对应角相等).
提示:要证明∠A= ∠C,可设法使它们分别在两个三角形中,为此,只要连接BD即可
3、已知:如图, AB=AC,DB=DC,F是AD延长线上的一点.
证明:
在△ ABD和△ ACD中
∵
AB=AC (已知)
DB=DC (已知)
AD=AD(公共边)
∴△ ABD ≌△ ACD (SSS)
∴∠BAD = ∠CAD (全等三角形的对应角相等).
在△BAF和△ CAF中
∵
AB=AC (已知)
∠BAF = ∠CAF (已证)
AF=AF (公共边)
∴△ BAF ≌△ CAF (SAS)
∴ ∠1 = ∠2 (全等三角形的对应角相等).
F
B
A
C
D
1
2
求证: ∠1 = ∠2
本节课你学习了哪些知识?
1、如何利用SSS证明两个三角形全等。
2、三角形具有稳定性。
边角边(SAS):
我们学过几种三角形的全等判定方法呢?
角边角(ASA):
两边及其夹角分别相等的两个三角形全等
两角及其夹边分别相等的两个三角形全等
1.经历探索三角形全等条件的过程(即如何用尺规作图:已知三边作三角形),体会利用操作、归纳获得数学结论的过程;
2.掌握全等三角形的判定方法“SSS”,并会运用该方法判断三角形是否全等,为证明线段相等或角相等创造条件;
3.了解三角形的稳定性.
学习重点:运用“SSS”证明两个三角形全等.
学习难点:寻求适当的方法证明三角形全等.
已知两个三角形的三条边都分别为3cm、4cm、6cm ,它们是否全等?
3cm
4cm
6cm
4cm
6cm
3cm
画全等三角形的另一个方法
如右上图,
画法:1、画线段A B =AB, 如右下图
2、分别以 A 、B 为圆心,AC、BC为半径画弧,两弧相交于点C .
3、连结A C 、 B C 得 A B C .
剪下 A B C 放在 ABC上,可以看到 A B C ≌ ABC,由此可以得到判定两个三角形全等的又一个方法.
A
B
C
A
B
C
已知任意 ABC,画一个 A B C ,
使A B =AB, A C =AC, B C =BC.
已知两个三角形的三条边都分别为3cm、4cm、6cm ,它们是否全等?
3cm
4cm
6cm
4cm
6cm
3cm
判定两个三角形全等的方法:
三边分别相等的两个三角形全等,简记为“边边边”或“SSS”
A
B
C
A
B
C
用数学语言表述:
在△ABC和△ A B C 中
∴ △ABC ≌△ A B C (SSS)
AB=A B BC= B C AC=A C
∵
思考:你能用“边边边”解释 三角形具有稳定性吗?
注: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。
1、下面四个三角形中,全等的是( )和( )
4
①
6
8
4
③
6
8
5
7
7
②
7
7
4
④
①
③
2.下列说法中,正确的有( )个
①周长相等的两个三角形全等,②面积相等的两个三角形全等,③有三个角对应相等的两个三角形全等,④有三边对应相等的两个三角形全等
A、1 B、2 C、3 D、4
A
例5. 如下图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF
证明:∵BE=CF (已知)
∴BE+EC=CF+CE(等式性质)
即BC=EF
在△ABC和△DEF中
AB=DE (已知)
AC=DF (已知)
BC=EF(已证)
∴△ABC≌△DEF (SSS)
∴∠B=∠DEF, ∠ACB=∠F(全等三角形的对应角相等)
∴AB ∥DE,AC∥DF(同位角相等两直线平行)
∵
A
F
B
E
C
D
C
O
A
B
如图,OA=OB,AC=BC. 求证:∠AOC=∠BOC.
∵
OA=OB
AC=BC
OC=OC
(公共边)
(已知)
(已知)
∴△ AOC ≌△ BOC (SSS)
在△ AOC 和△ BOC中
证明:
练 习 1
∴∠AOC=∠BOC
(全等三角形的对应角相等)
练 习 2
已知:如图,AB=CD,AD=CB.
求证: ∠A= ∠C.
证明:
连接BD
在 ABD 和 CDB中
∵
AB = CD (已知)
AD = CB (已知)
BD = DB (公共边)
∴ ABD ≌ CDB (SSS)
∴∠A = ∠C (全等三角形的对应角相等).
提示:要证明∠A= ∠C,可设法使它们分别在两个三角形中,为此,只要连接BD即可
3、已知:如图, AB=AC,DB=DC,F是AD延长线上的一点.
证明:
在△ ABD和△ ACD中
∵
AB=AC (已知)
DB=DC (已知)
AD=AD(公共边)
∴△ ABD ≌△ ACD (SSS)
∴∠BAD = ∠CAD (全等三角形的对应角相等).
在△BAF和△ CAF中
∵
AB=AC (已知)
∠BAF = ∠CAF (已证)
AF=AF (公共边)
∴△ BAF ≌△ CAF (SAS)
∴ ∠1 = ∠2 (全等三角形的对应角相等).
F
B
A
C
D
1
2
求证: ∠1 = ∠2
本节课你学习了哪些知识?
1、如何利用SSS证明两个三角形全等。
2、三角形具有稳定性。
