沪科版八年级上册 14.2.4三角形全等的判定定理4(AAS) 课件(共13张PPT)
文档属性
| 名称 | 沪科版八年级上册 14.2.4三角形全等的判定定理4(AAS) 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 242.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
14.2全等三角形的判定(4)
AAS
⒈已学过判定三角形全等的方法有——————
———————————————————
SAS、
ASA、
复习回顾:
2.已知:AB,CD交于O,且AO=BO,要证
△AOC≌△BOD,只需再添一个条件。
可以是________或________
SSS
定义、
OC=OD
∠A=∠B
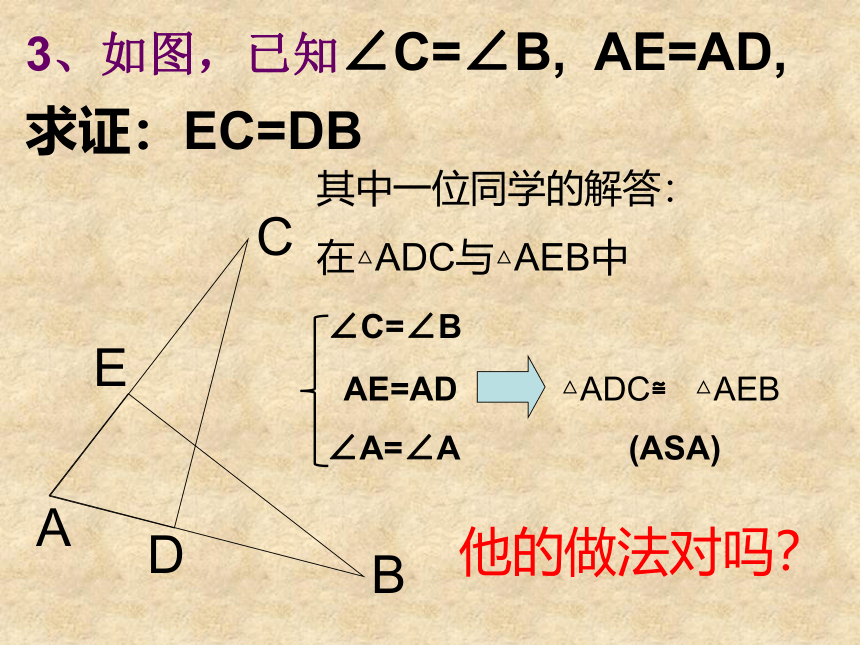
3、如图,已知∠C=∠B, AE=AD,
求证:EC=DB
C
E
B
D
A
其中一位同学的解答:
在△ADC与△AEB中
∠C=∠B
AE=AD △ADC≌ △AEB
∠A=∠A (ASA)
他的做法对吗?
已知在△ABC与△MNP中,∠A=∠M,∠B=∠N,BC=NP.
△ABC≌△MNP吗 为什么
B
C
A
?
N
P
M
?
思考
ASA AAS(三角形内角和)
两角和其中一角的对边对应相等的两个三角形全等。
(简写成“角角边”或“AAS”)
三角形全等的判定定理:
例题讲解
如图,点B、F、C、D在一条直线上,AB=ED, AB∥ED, AC∥EF
求证:△ABC≌△EDF
E
D
C
F
B
A
证明:∵ AB∥ED, AC∥EF
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
1、课本P107 练习 1、2
2、OP是∠MON的角平分线,C是OP上的一点,CA⊥OM,BC⊥ON,垂足分别为A、B,△AOC≌△BOC吗 为什么
O
B
N
C
P
A
M
若改变C在OP上的位置,那么△AOC与△BOC仍全等吗?你能发现什么结论?
角平分线上的点到角的两边的距离相等。
1、∠1=∠2,∠ABC=∠DCB,
求证:AC=DB.
B
C
A
D
1
2
2、已知:∠1=∠2,∠B=∠C,
AD=AE.
求证:AB=AC.
A
B
C
E
D
1
2
A
B
C
D
F
E
3、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.
求证:DE=BF.
4、如图:CD⊥AB于D,BE⊥AC于E,BE、CD交于点P,且∠1=∠2,
求证:PB=PC.
D
B
P
E
C
A
1
2
5、已知:BC=EF,BC∥EF,
∠A=∠D,∠ABF=∠DEC.
求证:AF=DC.
A
B
F
E
C
D
1.这节课你有哪些收获
2.列举判定的方法。
3.角平分线的性质。
14.2全等三角形的判定(4)
AAS
⒈已学过判定三角形全等的方法有——————
———————————————————
SAS、
ASA、
复习回顾:
2.已知:AB,CD交于O,且AO=BO,要证
△AOC≌△BOD,只需再添一个条件。
可以是________或________
SSS
定义、
OC=OD
∠A=∠B
3、如图,已知∠C=∠B, AE=AD,
求证:EC=DB
C
E
B
D
A
其中一位同学的解答:
在△ADC与△AEB中
∠C=∠B
AE=AD △ADC≌ △AEB
∠A=∠A (ASA)
他的做法对吗?
已知在△ABC与△MNP中,∠A=∠M,∠B=∠N,BC=NP.
△ABC≌△MNP吗 为什么
B
C
A
?
N
P
M
?
思考
ASA AAS(三角形内角和)
两角和其中一角的对边对应相等的两个三角形全等。
(简写成“角角边”或“AAS”)
三角形全等的判定定理:
例题讲解
如图,点B、F、C、D在一条直线上,AB=ED, AB∥ED, AC∥EF
求证:△ABC≌△EDF
E
D
C
F
B
A
证明:∵ AB∥ED, AC∥EF
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
1、课本P107 练习 1、2
2、OP是∠MON的角平分线,C是OP上的一点,CA⊥OM,BC⊥ON,垂足分别为A、B,△AOC≌△BOC吗 为什么
O
B
N
C
P
A
M
若改变C在OP上的位置,那么△AOC与△BOC仍全等吗?你能发现什么结论?
角平分线上的点到角的两边的距离相等。
1、∠1=∠2,∠ABC=∠DCB,
求证:AC=DB.
B
C
A
D
1
2
2、已知:∠1=∠2,∠B=∠C,
AD=AE.
求证:AB=AC.
A
B
C
E
D
1
2
A
B
C
D
F
E
3、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.
求证:DE=BF.
4、如图:CD⊥AB于D,BE⊥AC于E,BE、CD交于点P,且∠1=∠2,
求证:PB=PC.
D
B
P
E
C
A
1
2
5、已知:BC=EF,BC∥EF,
∠A=∠D,∠ABF=∠DEC.
求证:AF=DC.
A
B
F
E
C
D
1.这节课你有哪些收获
2.列举判定的方法。
3.角平分线的性质。
