北师大版八年级数学上册7.5三角形的内角和定理 课时精练(附答案)
文档属性
| 名称 | 北师大版八年级数学上册7.5三角形的内角和定理 课时精练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 99.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 09:01:15 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版八年级数学上册三角形的内角和定理课时精练(附答案)
一、单选题
1.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB= ∠CGE.其中正确的结论是( )
A. ②③ B. ①②④ C. ①③④ D. ①②③④
2.在△ABC中,∠A=75°,∠B=55°,则下列关于∠C的说法正确的是( )
A. 它是个钝角 B. 它等于70° C. 它是个锐角 D. 它是个直角
3.如图,在 中, , ,在 中, , , , 相交于点 ,有下列四个结论:① ;② 平分 ;③ ;④ .其中,正确的结论有( )
A. ①②③④ B. ①③④ C. ②③ D. ②③④
4.在 中, , , 的对边分别是 , , ,下列条件中,能判断 是直角三角形的是( )
A. B. , ,
C. , D.
5.等腰三角形一腰上的高与另一腰的夹角为 ,则其底角为( )
A. B. C. 或 D. 或
二、填空题
6.如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=115°,则∠A=________.
7.如图,将 ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B的大小为________度.
8.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
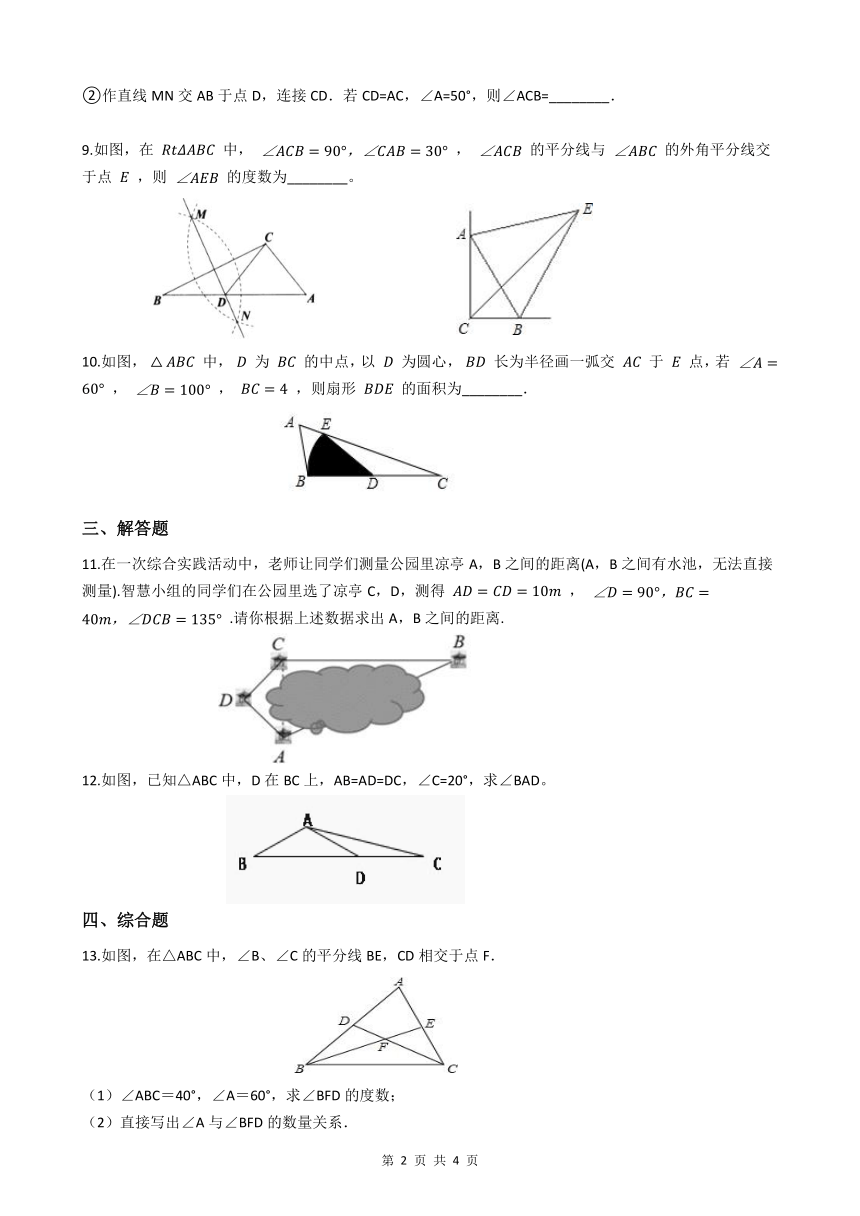
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB=________.
9.如图,在 中, , 的平分线与 的外角平分线交于点 ,则 的度数为________。
10.如图, 中, 为 的中点,以 为圆心, 长为半径画一弧交 于 点,若 , , ,则扇形 的面积为________.
三、解答题
11.在一次综合实践活动中,老师让同学们测量公园里凉亭A,B之间的距离(A,B之间有水池,无法直接测量).智慧小组的同学们在公园里选了凉亭C,D,测得 , .请你根据上述数据求出A,B之间的距离.
12.如图,已知△ABC中,D在BC上,AB=AD=DC,∠C=20°,求∠BAD。
四、综合题
13.如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度数;
(2)直接写出∠A与∠BFD的数量关系.
14.如图,在△ABC中,AB=AC,DE垂直平分AB.
(1)若AB=AC=10cm,BC=6cm,求△BCE的周长;
(2)若∠A=40°,求∠EBC的度数.
答 案
一、单选题
1. B 2. C 3. D 4. D 5. C
二、填空题
6. 50° 7. 114 8. 105° 9. 45° 10.
三、解答题
11. 解:连接
在 中, ,
由勾股定理得
在 中, ,
由勾股定理得
答:A,B之间的距离为
12. 解:题中给出了相等的边,以及角的度数,再让求其它角的度数,这就需要利用“等边对等角”、“三角形的内角和是180°”,以及三角形的内角与外角的关系进行解答.
∵AD=DC,∴∠DAC=∠C=20°,
∴∠ADB=∠DAC+∠C=40°.
∵AB=AD,∴∠B=∠ADB=40°,
∴∠BAD=180°-∠B-∠ADB=180°-40°-40°=100°.
四、综合题
13. (1)解:∵∠ABC=40°,∠A=60°,
∴∠ACB=180°﹣40°﹣60°=80°,
∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB= ∠ABC+ ∠ACB=20°+40°=60°.
(2)解:∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)= (180°﹣∠A)=90°﹣ ∠A.
14. (1)解:∵DE垂直平分AB, ∴EA=EB,
∵AB=AC=10cm,BC=6cm,
∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=10cm+6cm=16cm
(2)解:∵AB=AC,∠A=40°, ∴∠ABC=∠C=70°,
∵EA=EB,∠A=40°,∴∠A=∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°.
(
第
1
页 共
5
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版八年级数学上册三角形的内角和定理课时精练(附答案)
一、单选题
1.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB= ∠CGE.其中正确的结论是( )
A. ②③ B. ①②④ C. ①③④ D. ①②③④
2.在△ABC中,∠A=75°,∠B=55°,则下列关于∠C的说法正确的是( )
A. 它是个钝角 B. 它等于70° C. 它是个锐角 D. 它是个直角
3.如图,在 中, , ,在 中, , , , 相交于点 ,有下列四个结论:① ;② 平分 ;③ ;④ .其中,正确的结论有( )
A. ①②③④ B. ①③④ C. ②③ D. ②③④
4.在 中, , , 的对边分别是 , , ,下列条件中,能判断 是直角三角形的是( )
A. B. , ,
C. , D.
5.等腰三角形一腰上的高与另一腰的夹角为 ,则其底角为( )
A. B. C. 或 D. 或
二、填空题
6.如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=115°,则∠A=________.
7.如图,将 ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B的大小为________度.
8.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB=________.
9.如图,在 中, , 的平分线与 的外角平分线交于点 ,则 的度数为________。
10.如图, 中, 为 的中点,以 为圆心, 长为半径画一弧交 于 点,若 , , ,则扇形 的面积为________.
三、解答题
11.在一次综合实践活动中,老师让同学们测量公园里凉亭A,B之间的距离(A,B之间有水池,无法直接测量).智慧小组的同学们在公园里选了凉亭C,D,测得 , .请你根据上述数据求出A,B之间的距离.
12.如图,已知△ABC中,D在BC上,AB=AD=DC,∠C=20°,求∠BAD。
四、综合题
13.如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度数;
(2)直接写出∠A与∠BFD的数量关系.
14.如图,在△ABC中,AB=AC,DE垂直平分AB.
(1)若AB=AC=10cm,BC=6cm,求△BCE的周长;
(2)若∠A=40°,求∠EBC的度数.
答 案
一、单选题
1. B 2. C 3. D 4. D 5. C
二、填空题
6. 50° 7. 114 8. 105° 9. 45° 10.
三、解答题
11. 解:连接
在 中, ,
由勾股定理得
在 中, ,
由勾股定理得
答:A,B之间的距离为
12. 解:题中给出了相等的边,以及角的度数,再让求其它角的度数,这就需要利用“等边对等角”、“三角形的内角和是180°”,以及三角形的内角与外角的关系进行解答.
∵AD=DC,∴∠DAC=∠C=20°,
∴∠ADB=∠DAC+∠C=40°.
∵AB=AD,∴∠B=∠ADB=40°,
∴∠BAD=180°-∠B-∠ADB=180°-40°-40°=100°.
四、综合题
13. (1)解:∵∠ABC=40°,∠A=60°,
∴∠ACB=180°﹣40°﹣60°=80°,
∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB= ∠ABC+ ∠ACB=20°+40°=60°.
(2)解:∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)= (180°﹣∠A)=90°﹣ ∠A.
14. (1)解:∵DE垂直平分AB, ∴EA=EB,
∵AB=AC=10cm,BC=6cm,
∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=10cm+6cm=16cm
(2)解:∵AB=AC,∠A=40°, ∴∠ABC=∠C=70°,
∵EA=EB,∠A=40°,∴∠A=∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°.
(
第
1
页 共
5
页
)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
