高中数学人教A版2019必修第二册 9.1.2分层随机抽样 教学设计(表格式)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 9.1.2分层随机抽样 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览




文档简介
9.1.2 分层随机抽样
本节《普通高中课程标准数学教科书-必修二(人教A版)第九章《9.1.2 分层抽样》,本节的主要内容在本章的结构上,通过大背景的“串联”,从大背景中不断提出新问题,从而通过问题链进行探究学习,合理选择抽样方法的必要性并掌握分层抽样方法。从而发展学生的直观想象、逻辑推理、数学建模的核心素养。
课程目标 学科素养
A.理解分层抽样的基本思想和适用情形. B.掌握分层抽样的实施步骤. C.了解二种抽样方法的区别和联系. 1.数学建模:结合实际问题情景,理解分层抽样的必要性和重要性; 2.逻辑推理:学会用分层抽样的方法从总体中抽取样本; 3.直观想象: 对简单随机抽样、分层抽样方法进行比较,揭示其相互关系. 4.数学运算:总体平均数的估计方法
1.教学重点:理解分层抽样的基本思想和适用情形..
2.教学难点: 掌握分层抽样的实施步骤,会计算总体平均数.
多媒体
教学过程 教学设计意图 核心素养目标
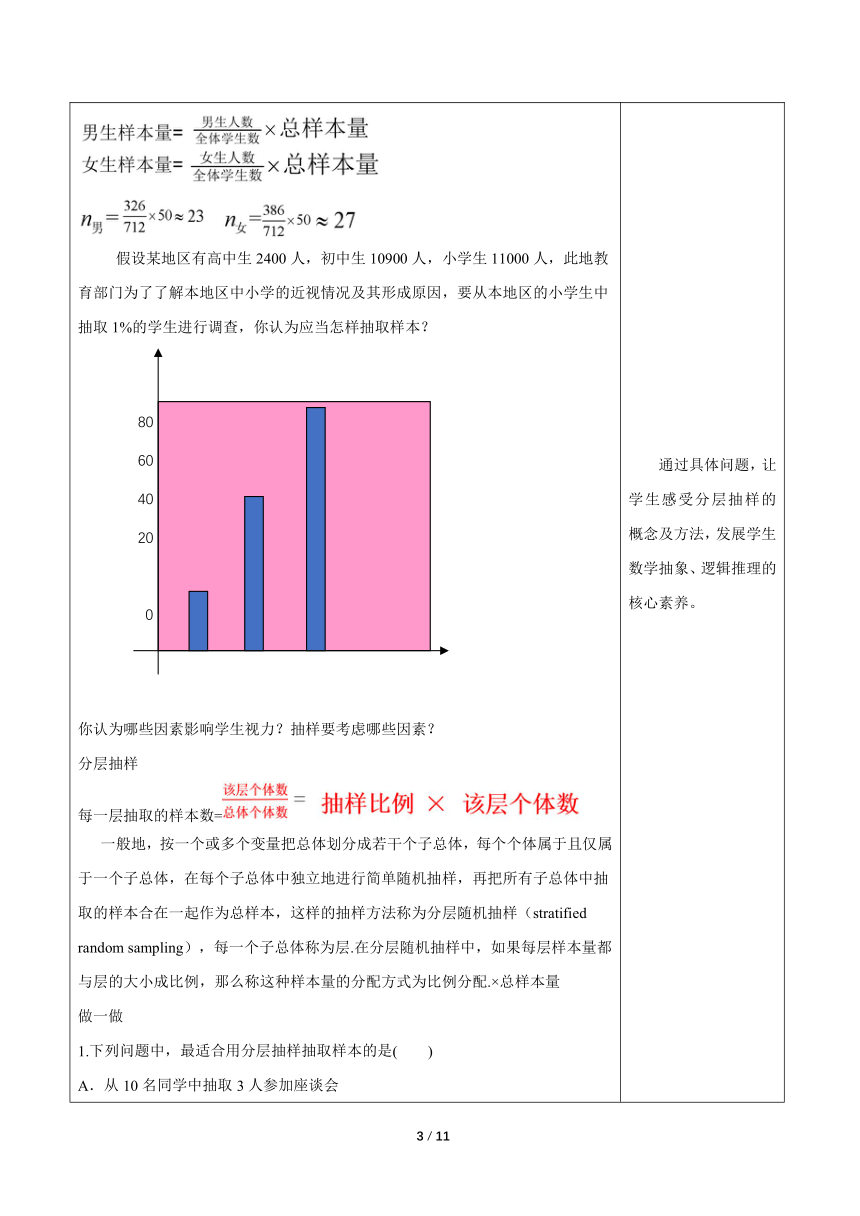
一、温故知新 1、简单随机抽样的概念: 设一个总体含有有限个个体,并记其个体数为N.如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的机会相等,就称这样的抽样为简单随机抽样. 2、简单随机抽样的特点: ①总体个数有限;②逐个进行抽取;③机会均等抽样. 3、简单随机抽样的常用方法: ①抽签法; ②随机数表法. 抽样调查最核心的问题是样本的代表性,简单随机抽样是使总体中每一个个体都有相等的机会被抽中,但因为抽样的随机性,有可能会出现比较“极端”的样本, 二、问题探究 例如,在对树人中学高一年级学生身高的调查中,可能出现样本中50个个体大部分来自高个子或矮个子的情形,这种“极端”样本的平均数会大幅度地偏离总体平均数,从而使得估计出现较大的误差. 能否利用总体中的一些额外信息对抽样方法进行改进呢? 在对树人中学高一年级学生身高的调查中, 采取简单随机抽样的方式抽取了50名学生。 1.抽样调查最核心的问题是什么? 2.会不会出现样本中 50 个个体大部分来自高个子或矮个子的情形? 3.为什么会出现这种“极端样本”? 4.如何避免这种“极端样本”? 样本代表性;会;抽样结果的随机性个体差异较大;分组抽样,减少组内差距 在树人中学高一年级的 712 名学生中, 男生有 326 名、女生有 386 名。 样本量在男生、女生中应如何分配? 假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本? 你认为哪些因素影响学生视力?抽样要考虑哪些因素? 分层抽样 每一层抽取的样本数= 一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.×总样本量 做一做 1.下列问题中,最适合用分层抽样抽取样本的是( ) A.从10名同学中抽取3人参加座谈会 B.某社区有500个家庭,其中高收入的家庭125个,中等收入的家庭280个,低收入的家庭95个,为了了解生活购买力的某项指标,要从中抽取一个容量为100的样本 C.从1 000名工人中,抽取100名调查上班途中所用时间 D.从生产流水线上,抽取样本检查产品质量 【解析】A中总体个体无明显差异且个数较少,适合用简单随机抽样;C和D中总体个体无明显差异且个数较多,适合用系统抽样;B中总体个体差异明显,适合用分层抽样. 【答案】 B 2.某公司生产三种型号的轿车,产量分别是1 200辆,6 000辆和2 000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取________辆、________辆、________辆. 【解析】 三种型号的轿车共9 200辆,抽取样本为46辆,则按=的比例抽样,所以依次应抽取1 200×=6(辆),6 000×=30(辆),2 000×=10(辆). 【答案】 6 30 10 1.分层抽样的步骤 2.分层抽样的特点有哪些? 【提示】 (1)分层抽样适用于已知总体是由差异明显的几部分组成的;(2)分成的各层互不交叉;(3)各层抽取的比例都等于样本容量在总体中的比例,即,其中n为样本容量,N为总体容量. 3. 计算各层所抽取个体的个数时,若Ni·的值不是整数怎么办? 【提示】 为获取各层的入样数目,需先正确计算出抽样比,若Ni·的值不是整数,可四舍五入取整,也可先将该层等可能地剔除多余的个体. 探究3 分层抽样公平吗? 【提示】 分层抽样中,每个个体被抽到的可能性是相同的,与层数、分层无关. 如果总体的个数为N,样本容量为n,Ni为第i层的个体数,则第i层抽取的个体数ni=n·,每个个体被抽到的可能性是=·n·=. 4. 简单随机抽样、分层抽样的各自特点及适用范围有什么异同? 【提示】 简单随机抽样是最基本的抽样方法,应用于系统抽样和分层抽样中.简单随机抽样所得样本的代表性与个体编号无关. 分层抽样应用最广泛,它充分利用总体信息,得到的样本比前两种抽样方法都具有代表性. 分层随机抽样的平均数 两种抽样方法的特点及其适用范围如下表: 类别简单随机抽样分层抽样各自 特点从总体中逐个抽取将总体分成几层,分层进行抽取相互 联系在各层抽样时采用简单随机抽样或系统抽样适用 范围总体中的个体数较少总体由存在明显差异的几部分组成
1.在简单随机抽样中如何估计总体平均数? 2.那么在分层随机抽样中如何估计总体平均数呢? 是否也可以直接用样本平均数进行估计? (1)在分层随机抽样中,如果层数分为2层,第1层和第2层包含的个体数分别为M和N,抽取的样本量分别为m和n.我们用X1,X2,…,XM表示第1层各个个体的变量值,用x1,x2,…,xm表示第1层样本的各个个体的变量值;用Y1,Y2,…,YN表示第2层各个个体的变量值,用y1,y2,…,yn表示第2层样本的各个个体的变量值,则: 分层随机抽样中的总体平均数与样本平均数 第1层的总体平均数和样本平均数为: 第2层的总体平均数和样本平均数为: 总体平均数和样本平均数为: 由于用第一层的样本平均数 可以估计第1层的总体平均数 ,第二层的样本平均数 可以估计第2层的总体平均数,因此我们可以用 估计总体平均数 对各层样本平均数加权(层权)求和 ; 分层随机抽样如何估计总体平均数 在比例分配的分层随机中抽样中 例1.在树人中学高一年级的 712 名学生,男生有 326 名、女生有 386 名,分别抽取的男生23名男生、27名女生样本数据如下 173.0174.0166.0172.0170.0165.0165.0168.0164.0173.0172.0173.0175.0168.0170.0172.0176.0175.0168.0173.0167.0170.0175.0
163.0164.0161.0157.0162.0165.0168.0155.0164.0162.5154.0154.0164.0149.0159.0161.0170.0171.0155.0148.0172.0162.5158.0155.5157.0163.0172.0
样本女生平均身高=160.6,样本男生平均身高=170.6 高一年级有男生490人,女生510人,张华按照男生女生进行分层,得到男生女生平均身高分别为170.2cm和160.8cm。 (1)如果张华在各层中按比例分配样本,总样本量为100.那么男生、女生中分别抽取了多少名?在这种情况下,请估计高一年级全体学生的平均身高。 (2)如果张华从男生、女生中抽取的样本量分别为30和70,那么在这种情况下,如何估计高一全体学生的平均身高。 小明用比例分配的分层抽样方法,从高一年级的学生中抽取了十个样本量为50的样本,计算出样本平均数。与相同样本量的简单随机抽样的结果比较。 序号12345678910简单随机抽样165.2162.8164.4164.4165.6164.8165.3164.3165.7165.0分层随机抽样165.8 165.1 164.3 164.3 166.4 164.6 165.2164.9 166.1 165.1
由生活中的问题出发,提出问题,让学生感受到采用分层抽样的必要性。发展学生数学抽象、直观想象和逻辑推理的核心素养。 通过具体问题,让学生感受分层抽样的概念及方法,发展学生数学抽象、逻辑推理的核心素养。 通过实例分析,让学生掌握分层抽样的基本步骤,并熟悉的应用能力,提升推理论证能力,提高学生的数学抽象、数学建模及逻辑推理的核心素养。
三、达标检测 1.下列实验中最适合用分层抽样法抽样的是( ) A.从一箱3 000个零件中抽取5个入样 B.从一箱3 000个零件中抽取600个入样 C.从一箱30个零件中抽取5个入样 D.从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样 【答案】 D 【解析】 D中总体有明显差异,故用分层抽样. 2.一批灯泡400只,其中20 W、40 W、60 W的数目之比是4∶3∶1,现用分层抽样的方法产生一个容量为40的样本,三种灯泡依次抽取的个数为( ) A.20,15,5 B.4,3,1 C.16,12,4 D.8,6,2 【答案】 A【解析】 三种灯泡依次抽取的个数为40×=20,40×=15,40×=5. 3.某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上(包括50岁)的人,用分层抽样的方法从中抽20人,各年龄段分别抽取的人数为( ) A.7,5,8 B.9,5,6 C.7,5,9 D.8,5,7 【答案】 B 【解析】 由于样本容量与总体个体数之比为=,故各年龄段抽取的人数依次为45×=9(人), 25×=5(人),20-9-5=6(人). 4.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格: 产品类型ABC产品数量(件)1 300样本容量130
由于不小心,表格中A,C两种产品的有关数据已被污染看不清楚了,统计员只记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是________件. 【解析】 抽样比为130∶1 300=1∶10,即每10个产品中抽取1个个体,又A产品的样本容量比C产品的样本容量多10,故C产品的数量是[(3 000-1 300)-100]×=800(件). 【答案】 800 5.某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表: 第一车间第二车间第三车间女工173100y男工177xz
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0.15. (1)求x的值; (2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名? 【解】 (1)由=0.15,得x=150. (2)∵第一车间的工人数是173+177=350,第二车间的工人数是100+150=250, ∴第三车间的工人数是1 000-350-250=400. 设应从第三车间抽取m名工人,则由=,得m=20. ∴应在第三车间抽取20名工人. 通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学抽象、逻辑推理、数学运算、数学建模的核心素养。
四、小结 1、分层抽样是当总体由差异明显的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点: (1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是,层内样本的差异要小,面层之间的样本差异要大,且互不重叠。 (2)为了保证每个个体等可能入样,所有层应采用同一抽样比等可能抽样。 (3)在每层抽样时,应采用简单随机抽样的方法进行抽样。 2、分层抽样的优点是:使样本具有较强的代表性,并且抽样过程中可综合选用各种抽样方法,因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法。 3、分层随机抽样中如何用样本估计总体平均值。 ; 五、课时练 通过总结,让学生进一步巩固本节所学内容,提高概括能力。
本节的主要内容在本章的结构上,通过大背景的“串联”,从大背景中不断提出新问题,从而通过问题链进行探究学习,合理选择抽样方法的必要性并掌握分层抽样方法。从而发展学生的直观想象、逻辑推理、数学建模的核心素养。教学中要注重学生的主体地位,调动学生积极性,使数学教学成为数学活动的教学。
1 / 11
本节《普通高中课程标准数学教科书-必修二(人教A版)第九章《9.1.2 分层抽样》,本节的主要内容在本章的结构上,通过大背景的“串联”,从大背景中不断提出新问题,从而通过问题链进行探究学习,合理选择抽样方法的必要性并掌握分层抽样方法。从而发展学生的直观想象、逻辑推理、数学建模的核心素养。
课程目标 学科素养
A.理解分层抽样的基本思想和适用情形. B.掌握分层抽样的实施步骤. C.了解二种抽样方法的区别和联系. 1.数学建模:结合实际问题情景,理解分层抽样的必要性和重要性; 2.逻辑推理:学会用分层抽样的方法从总体中抽取样本; 3.直观想象: 对简单随机抽样、分层抽样方法进行比较,揭示其相互关系. 4.数学运算:总体平均数的估计方法
1.教学重点:理解分层抽样的基本思想和适用情形..
2.教学难点: 掌握分层抽样的实施步骤,会计算总体平均数.
多媒体
教学过程 教学设计意图 核心素养目标
一、温故知新 1、简单随机抽样的概念: 设一个总体含有有限个个体,并记其个体数为N.如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的机会相等,就称这样的抽样为简单随机抽样. 2、简单随机抽样的特点: ①总体个数有限;②逐个进行抽取;③机会均等抽样. 3、简单随机抽样的常用方法: ①抽签法; ②随机数表法. 抽样调查最核心的问题是样本的代表性,简单随机抽样是使总体中每一个个体都有相等的机会被抽中,但因为抽样的随机性,有可能会出现比较“极端”的样本, 二、问题探究 例如,在对树人中学高一年级学生身高的调查中,可能出现样本中50个个体大部分来自高个子或矮个子的情形,这种“极端”样本的平均数会大幅度地偏离总体平均数,从而使得估计出现较大的误差. 能否利用总体中的一些额外信息对抽样方法进行改进呢? 在对树人中学高一年级学生身高的调查中, 采取简单随机抽样的方式抽取了50名学生。 1.抽样调查最核心的问题是什么? 2.会不会出现样本中 50 个个体大部分来自高个子或矮个子的情形? 3.为什么会出现这种“极端样本”? 4.如何避免这种“极端样本”? 样本代表性;会;抽样结果的随机性个体差异较大;分组抽样,减少组内差距 在树人中学高一年级的 712 名学生中, 男生有 326 名、女生有 386 名。 样本量在男生、女生中应如何分配? 假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本? 你认为哪些因素影响学生视力?抽样要考虑哪些因素? 分层抽样 每一层抽取的样本数= 一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.×总样本量 做一做 1.下列问题中,最适合用分层抽样抽取样本的是( ) A.从10名同学中抽取3人参加座谈会 B.某社区有500个家庭,其中高收入的家庭125个,中等收入的家庭280个,低收入的家庭95个,为了了解生活购买力的某项指标,要从中抽取一个容量为100的样本 C.从1 000名工人中,抽取100名调查上班途中所用时间 D.从生产流水线上,抽取样本检查产品质量 【解析】A中总体个体无明显差异且个数较少,适合用简单随机抽样;C和D中总体个体无明显差异且个数较多,适合用系统抽样;B中总体个体差异明显,适合用分层抽样. 【答案】 B 2.某公司生产三种型号的轿车,产量分别是1 200辆,6 000辆和2 000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取________辆、________辆、________辆. 【解析】 三种型号的轿车共9 200辆,抽取样本为46辆,则按=的比例抽样,所以依次应抽取1 200×=6(辆),6 000×=30(辆),2 000×=10(辆). 【答案】 6 30 10 1.分层抽样的步骤 2.分层抽样的特点有哪些? 【提示】 (1)分层抽样适用于已知总体是由差异明显的几部分组成的;(2)分成的各层互不交叉;(3)各层抽取的比例都等于样本容量在总体中的比例,即,其中n为样本容量,N为总体容量. 3. 计算各层所抽取个体的个数时,若Ni·的值不是整数怎么办? 【提示】 为获取各层的入样数目,需先正确计算出抽样比,若Ni·的值不是整数,可四舍五入取整,也可先将该层等可能地剔除多余的个体. 探究3 分层抽样公平吗? 【提示】 分层抽样中,每个个体被抽到的可能性是相同的,与层数、分层无关. 如果总体的个数为N,样本容量为n,Ni为第i层的个体数,则第i层抽取的个体数ni=n·,每个个体被抽到的可能性是=·n·=. 4. 简单随机抽样、分层抽样的各自特点及适用范围有什么异同? 【提示】 简单随机抽样是最基本的抽样方法,应用于系统抽样和分层抽样中.简单随机抽样所得样本的代表性与个体编号无关. 分层抽样应用最广泛,它充分利用总体信息,得到的样本比前两种抽样方法都具有代表性. 分层随机抽样的平均数 两种抽样方法的特点及其适用范围如下表: 类别简单随机抽样分层抽样各自 特点从总体中逐个抽取将总体分成几层,分层进行抽取相互 联系在各层抽样时采用简单随机抽样或系统抽样适用 范围总体中的个体数较少总体由存在明显差异的几部分组成
1.在简单随机抽样中如何估计总体平均数? 2.那么在分层随机抽样中如何估计总体平均数呢? 是否也可以直接用样本平均数进行估计? (1)在分层随机抽样中,如果层数分为2层,第1层和第2层包含的个体数分别为M和N,抽取的样本量分别为m和n.我们用X1,X2,…,XM表示第1层各个个体的变量值,用x1,x2,…,xm表示第1层样本的各个个体的变量值;用Y1,Y2,…,YN表示第2层各个个体的变量值,用y1,y2,…,yn表示第2层样本的各个个体的变量值,则: 分层随机抽样中的总体平均数与样本平均数 第1层的总体平均数和样本平均数为: 第2层的总体平均数和样本平均数为: 总体平均数和样本平均数为: 由于用第一层的样本平均数 可以估计第1层的总体平均数 ,第二层的样本平均数 可以估计第2层的总体平均数,因此我们可以用 估计总体平均数 对各层样本平均数加权(层权)求和 ; 分层随机抽样如何估计总体平均数 在比例分配的分层随机中抽样中 例1.在树人中学高一年级的 712 名学生,男生有 326 名、女生有 386 名,分别抽取的男生23名男生、27名女生样本数据如下 173.0174.0166.0172.0170.0165.0165.0168.0164.0173.0172.0173.0175.0168.0170.0172.0176.0175.0168.0173.0167.0170.0175.0
163.0164.0161.0157.0162.0165.0168.0155.0164.0162.5154.0154.0164.0149.0159.0161.0170.0171.0155.0148.0172.0162.5158.0155.5157.0163.0172.0
样本女生平均身高=160.6,样本男生平均身高=170.6 高一年级有男生490人,女生510人,张华按照男生女生进行分层,得到男生女生平均身高分别为170.2cm和160.8cm。 (1)如果张华在各层中按比例分配样本,总样本量为100.那么男生、女生中分别抽取了多少名?在这种情况下,请估计高一年级全体学生的平均身高。 (2)如果张华从男生、女生中抽取的样本量分别为30和70,那么在这种情况下,如何估计高一全体学生的平均身高。 小明用比例分配的分层抽样方法,从高一年级的学生中抽取了十个样本量为50的样本,计算出样本平均数。与相同样本量的简单随机抽样的结果比较。 序号12345678910简单随机抽样165.2162.8164.4164.4165.6164.8165.3164.3165.7165.0分层随机抽样165.8 165.1 164.3 164.3 166.4 164.6 165.2164.9 166.1 165.1
由生活中的问题出发,提出问题,让学生感受到采用分层抽样的必要性。发展学生数学抽象、直观想象和逻辑推理的核心素养。 通过具体问题,让学生感受分层抽样的概念及方法,发展学生数学抽象、逻辑推理的核心素养。 通过实例分析,让学生掌握分层抽样的基本步骤,并熟悉的应用能力,提升推理论证能力,提高学生的数学抽象、数学建模及逻辑推理的核心素养。
三、达标检测 1.下列实验中最适合用分层抽样法抽样的是( ) A.从一箱3 000个零件中抽取5个入样 B.从一箱3 000个零件中抽取600个入样 C.从一箱30个零件中抽取5个入样 D.从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样 【答案】 D 【解析】 D中总体有明显差异,故用分层抽样. 2.一批灯泡400只,其中20 W、40 W、60 W的数目之比是4∶3∶1,现用分层抽样的方法产生一个容量为40的样本,三种灯泡依次抽取的个数为( ) A.20,15,5 B.4,3,1 C.16,12,4 D.8,6,2 【答案】 A【解析】 三种灯泡依次抽取的个数为40×=20,40×=15,40×=5. 3.某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上(包括50岁)的人,用分层抽样的方法从中抽20人,各年龄段分别抽取的人数为( ) A.7,5,8 B.9,5,6 C.7,5,9 D.8,5,7 【答案】 B 【解析】 由于样本容量与总体个体数之比为=,故各年龄段抽取的人数依次为45×=9(人), 25×=5(人),20-9-5=6(人). 4.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格: 产品类型ABC产品数量(件)1 300样本容量130
由于不小心,表格中A,C两种产品的有关数据已被污染看不清楚了,统计员只记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是________件. 【解析】 抽样比为130∶1 300=1∶10,即每10个产品中抽取1个个体,又A产品的样本容量比C产品的样本容量多10,故C产品的数量是[(3 000-1 300)-100]×=800(件). 【答案】 800 5.某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表: 第一车间第二车间第三车间女工173100y男工177xz
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0.15. (1)求x的值; (2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名? 【解】 (1)由=0.15,得x=150. (2)∵第一车间的工人数是173+177=350,第二车间的工人数是100+150=250, ∴第三车间的工人数是1 000-350-250=400. 设应从第三车间抽取m名工人,则由=,得m=20. ∴应在第三车间抽取20名工人. 通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学抽象、逻辑推理、数学运算、数学建模的核心素养。
四、小结 1、分层抽样是当总体由差异明显的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点: (1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是,层内样本的差异要小,面层之间的样本差异要大,且互不重叠。 (2)为了保证每个个体等可能入样,所有层应采用同一抽样比等可能抽样。 (3)在每层抽样时,应采用简单随机抽样的方法进行抽样。 2、分层抽样的优点是:使样本具有较强的代表性,并且抽样过程中可综合选用各种抽样方法,因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法。 3、分层随机抽样中如何用样本估计总体平均值。 ; 五、课时练 通过总结,让学生进一步巩固本节所学内容,提高概括能力。
本节的主要内容在本章的结构上,通过大背景的“串联”,从大背景中不断提出新问题,从而通过问题链进行探究学习,合理选择抽样方法的必要性并掌握分层抽样方法。从而发展学生的直观想象、逻辑推理、数学建模的核心素养。教学中要注重学生的主体地位,调动学生积极性,使数学教学成为数学活动的教学。
1 / 11
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
