数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 376.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 07:35:49 | ||
图片预览





文档简介
(共24张PPT)
空间向量的数量积运算
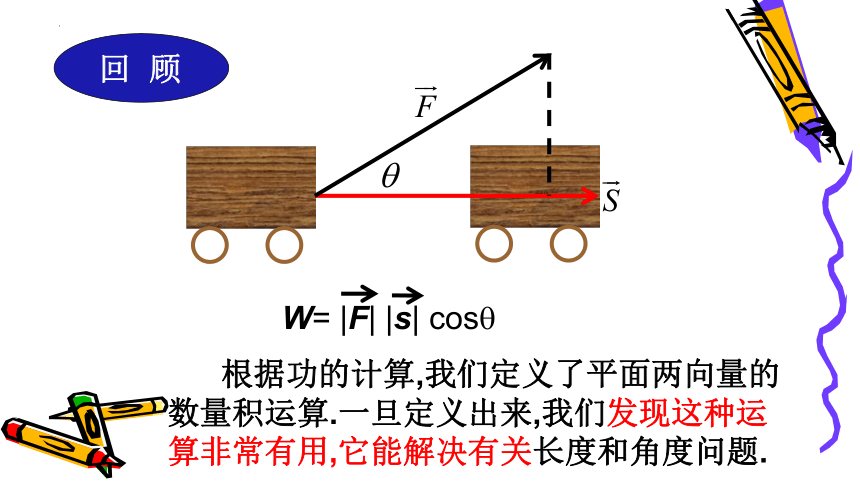
W= |F| |s| cos
根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.
回 顾
一 复习引入
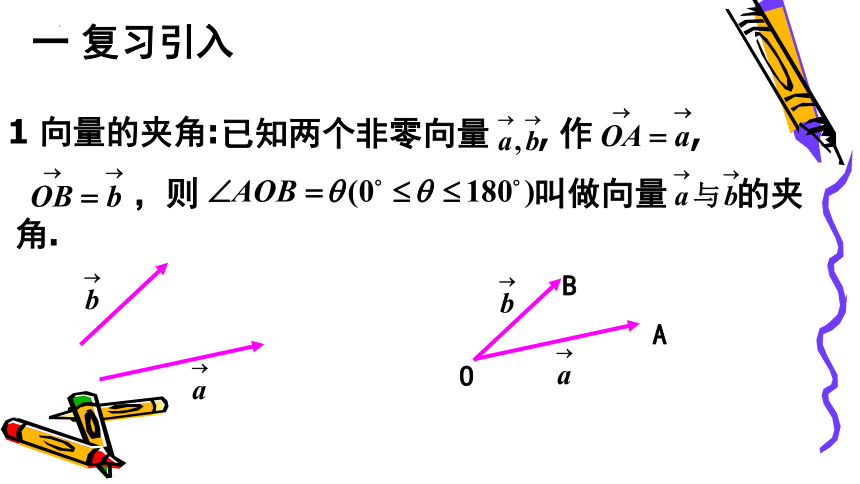
已知两个非零向量 , 作 ,
,则 叫做向量 的夹角.
1 向量的夹角:
O
A
B
已知两个非零向量 ,它们的夹角为 ,我们把 叫做向量 的数量积,记做 ,即 = .
2 平面向量数量积:
3 平面向量数量积的性质
4 平面向量数量积的运算律
(交换律)
(分配律)
(数乘结合律)
1)两个向量的夹角的定义:
O
A
B
知 新
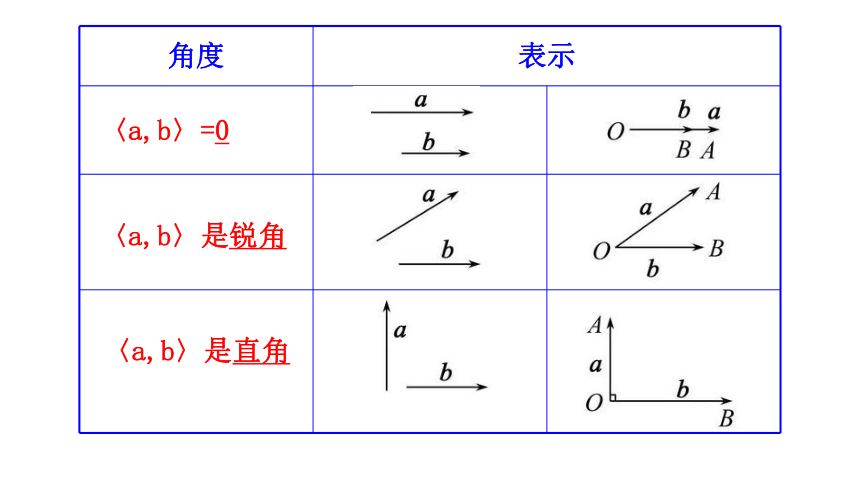
角度 表示
〈a,b〉=0
〈a,b〉是锐角
〈a,b〉是直角
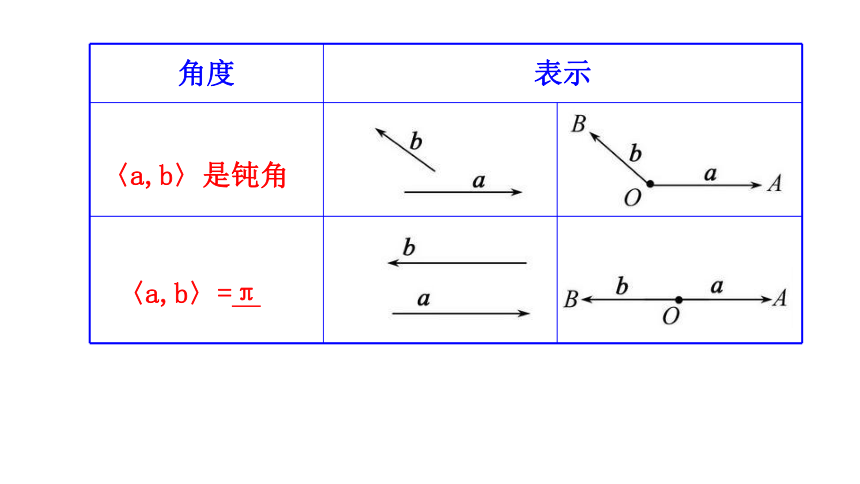
角度 表示
〈a,b〉是钝角
〈a,b〉=π
注:(1)两个向量的数量积是数量,而不是向量.
(2)规定:零向量与任意向量的数量积等于零.
(3)点乘符号“· ”在向量运算中不是乘号,既不能省略,也不能用“×”代替.
C'
D'
B'
A'
C
D
A
B
◆练习 已知正方体AC'边长为1,求:
数量积 等于 的长度 与 在
的方向上的投影 的乘积。
θ
B1
B
O
A
几何意义
3)空间两个向量的数量积性质
注:
性质②是证明两向量垂直的依据;
性质③是求向量的长度(模)的依据.
4)空间向量的数量积满足的运算律
注: 向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立。
思考1.
如
果不能,请举出反例
能
得到
吗?
由
,
对于三个均不为
0
的
数
a
,
b
,
c
,
若
ab
=
ac
,
则
b
=
c
.
对于向量
,
,
.
思考2.
对于三个均不为0的数
若 则
对于向量 若 能否
写成 也就是说
向量有除法吗?
思考3.
对于三个均不为0的数
对于向量
成立吗?也就是说,向量的数量积满足结合律吗?
课堂练习
A
D
F
C
B
E
4.
空间向量的数量积运算
W= |F| |s| cos
根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.
回 顾
一 复习引入
已知两个非零向量 , 作 ,
,则 叫做向量 的夹角.
1 向量的夹角:
O
A
B
已知两个非零向量 ,它们的夹角为 ,我们把 叫做向量 的数量积,记做 ,即 = .
2 平面向量数量积:
3 平面向量数量积的性质
4 平面向量数量积的运算律
(交换律)
(分配律)
(数乘结合律)
1)两个向量的夹角的定义:
O
A
B
知 新
角度 表示
〈a,b〉=0
〈a,b〉是锐角
〈a,b〉是直角
角度 表示
〈a,b〉是钝角
〈a,b〉=π
注:(1)两个向量的数量积是数量,而不是向量.
(2)规定:零向量与任意向量的数量积等于零.
(3)点乘符号“· ”在向量运算中不是乘号,既不能省略,也不能用“×”代替.
C'
D'
B'
A'
C
D
A
B
◆练习 已知正方体AC'边长为1,求:
数量积 等于 的长度 与 在
的方向上的投影 的乘积。
θ
B1
B
O
A
几何意义
3)空间两个向量的数量积性质
注:
性质②是证明两向量垂直的依据;
性质③是求向量的长度(模)的依据.
4)空间向量的数量积满足的运算律
注: 向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立。
思考1.
如
果不能,请举出反例
能
得到
吗?
由
,
对于三个均不为
0
的
数
a
,
b
,
c
,
若
ab
=
ac
,
则
b
=
c
.
对于向量
,
,
.
思考2.
对于三个均不为0的数
若 则
对于向量 若 能否
写成 也就是说
向量有除法吗?
思考3.
对于三个均不为0的数
对于向量
成立吗?也就是说,向量的数量积满足结合律吗?
课堂练习
A
D
F
C
B
E
4.
