数学人教A版(2019)必修第二册6.2.4向量的数量积 课件(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.2.4向量的数量积 课件(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 642.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 07:36:51 | ||
图片预览




文档简介
(共19张PPT)
6.2.4 向量的数量积
功的概念: 如果一辆车在力F的作用下产生位移s, 那么力F所做的功:
θ
其中θ是 与 的夹角.
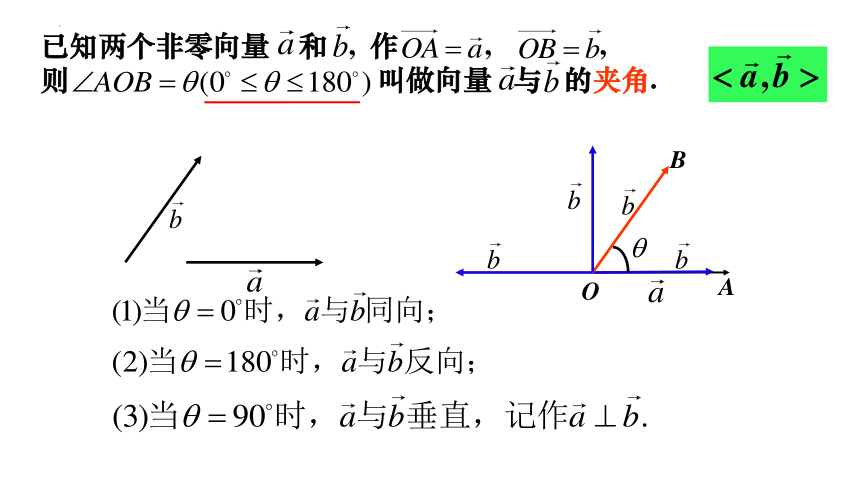
已知两个非零向量 和 , 作 , , 则 叫做向量 与 的夹角.
A
O
B
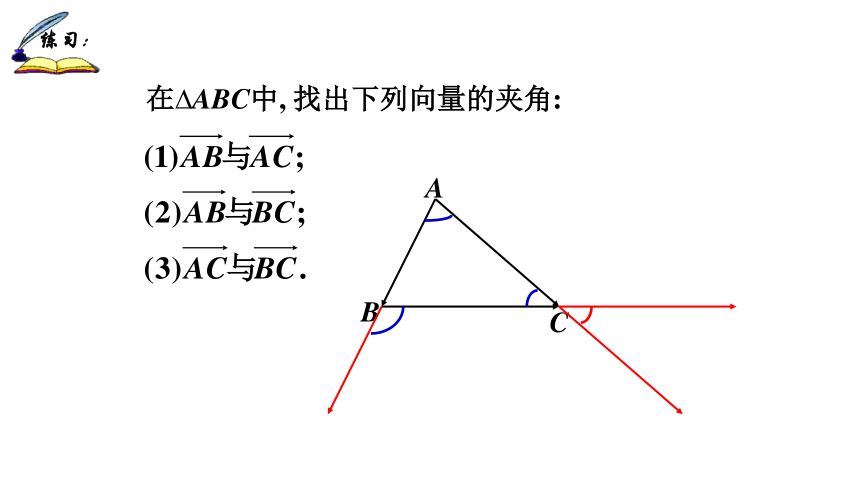
在 ABC中, 找出下列向量的夹角:
A
B
C
练习:
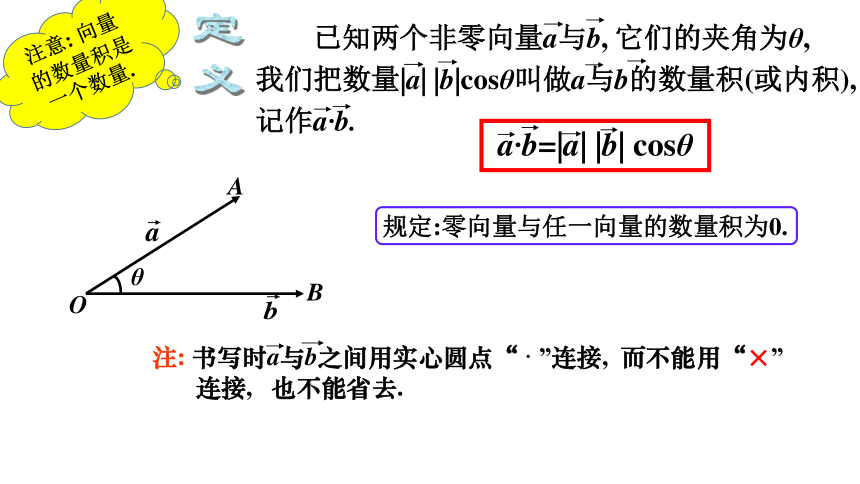
已知两个非零向量a与b, 它们的夹角为θ,
我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),
记作a·b.
定
义
规定:零向量与任一向量的数量积为0.
a·b=|a| |b| cosθ
B
θ
O
A
注意: 向量的数量积是一个数量.
注: 书写时a与b之间用实心圆点“ · ”连接, 而不能用“×”
连接, 也不能省去.
例1、已知| a |=5,| b |=4,a 与 b 的夹角为θ;
(1)当θ=0°时,求 a · b;
(2)当θ=180°时,求 a · b ;
(3)当θ=90°时,求 a · b;
(4)当θ=120°时,求 a · b;
(5)求 a · a。
几个有用的结论:设 a 和 b 都是非零向量,则有:
(1)a⊥b a · b=0。
(2)当 a 与 b 同向时, a · b =| a || b |;当 a 与 b 反向时, a · b=-| a || b |。
特别地,a ·a =| a |2 或 | a |
(3)a · b 的符号由θ 决定
练习
数量积的运算律:
其中,
是任意三个向量,
例2、对任意的向量 ,试证明:
例3、已知 , 且 与 的夹角为60°,
(1)求
(2)k为何值时,向量 与 互相垂直?
(3)试求 的值。
作业:
习题6.2.4 P23 T11 T18
a·b=|a| |b| cosθ
6.2.4 向量的数量积(二)
定
义
规定:零向量与任一向量的数量积为0.
知识回顾
几个有用的结论:
(1)a · b 的正负由θ决定;
(2)a⊥b a · b=0;(a 和 b 都是非零向量)
(3)a 2=| a |2 或 | a |
A
θ
O
B
已知两个非零向量a与b, 它们的夹角为θ,
我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),
记作a·b.
练习:
1. 已知平面向量 则
2.已知向量a, b的夹角为300, 且|a|= , |b|=2, 求向量p=a+b与q=a-b
的夹角θ的余弦值.
已知两个非零向量a与b, 它们的夹角为θ,
我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),
记作a·b.
定
义
规定:零向量与任一向量的数量积为0.
A
θ
O
B
定义再回顾
B1
B
D1
C
A
C1
D
——
A
O
B
θ
B1
探究:
M1
N
θ
O
M
(1)锐角
M1
N
θ
O
M
(2)直角
M1
N
θ
O
M
(3)钝角
B1
O
A1
C
证明运算律
A
B
D
D1
练习
√
√
√
6.已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.则向量a在向量a+b上的
投影向量的模为_______.
6.2.4 向量的数量积
功的概念: 如果一辆车在力F的作用下产生位移s, 那么力F所做的功:
θ
其中θ是 与 的夹角.
已知两个非零向量 和 , 作 , , 则 叫做向量 与 的夹角.
A
O
B
在 ABC中, 找出下列向量的夹角:
A
B
C
练习:
已知两个非零向量a与b, 它们的夹角为θ,
我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),
记作a·b.
定
义
规定:零向量与任一向量的数量积为0.
a·b=|a| |b| cosθ
B
θ
O
A
注意: 向量的数量积是一个数量.
注: 书写时a与b之间用实心圆点“ · ”连接, 而不能用“×”
连接, 也不能省去.
例1、已知| a |=5,| b |=4,a 与 b 的夹角为θ;
(1)当θ=0°时,求 a · b;
(2)当θ=180°时,求 a · b ;
(3)当θ=90°时,求 a · b;
(4)当θ=120°时,求 a · b;
(5)求 a · a。
几个有用的结论:设 a 和 b 都是非零向量,则有:
(1)a⊥b a · b=0。
(2)当 a 与 b 同向时, a · b =| a || b |;当 a 与 b 反向时, a · b=-| a || b |。
特别地,a ·a =| a |2 或 | a |
(3)a · b 的符号由θ 决定
练习
数量积的运算律:
其中,
是任意三个向量,
例2、对任意的向量 ,试证明:
例3、已知 , 且 与 的夹角为60°,
(1)求
(2)k为何值时,向量 与 互相垂直?
(3)试求 的值。
作业:
习题6.2.4 P23 T11 T18
a·b=|a| |b| cosθ
6.2.4 向量的数量积(二)
定
义
规定:零向量与任一向量的数量积为0.
知识回顾
几个有用的结论:
(1)a · b 的正负由θ决定;
(2)a⊥b a · b=0;(a 和 b 都是非零向量)
(3)a 2=| a |2 或 | a |
A
θ
O
B
已知两个非零向量a与b, 它们的夹角为θ,
我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),
记作a·b.
练习:
1. 已知平面向量 则
2.已知向量a, b的夹角为300, 且|a|= , |b|=2, 求向量p=a+b与q=a-b
的夹角θ的余弦值.
已知两个非零向量a与b, 它们的夹角为θ,
我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),
记作a·b.
定
义
规定:零向量与任一向量的数量积为0.
A
θ
O
B
定义再回顾
B1
B
D1
C
A
C1
D
——
A
O
B
θ
B1
探究:
M1
N
θ
O
M
(1)锐角
M1
N
θ
O
M
(2)直角
M1
N
θ
O
M
(3)钝角
B1
O
A1
C
证明运算律
A
B
D
D1
练习
√
√
√
6.已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.则向量a在向量a+b上的
投影向量的模为_______.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
