贵州省铜仁市第十一中学2022-2023学年九年级上册数学期中测试题(PDF版无答案)
文档属性
| 名称 | 贵州省铜仁市第十一中学2022-2023学年九年级上册数学期中测试题(PDF版无答案) |
|
|
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-29 00:00:00 | ||
图片预览

文档简介
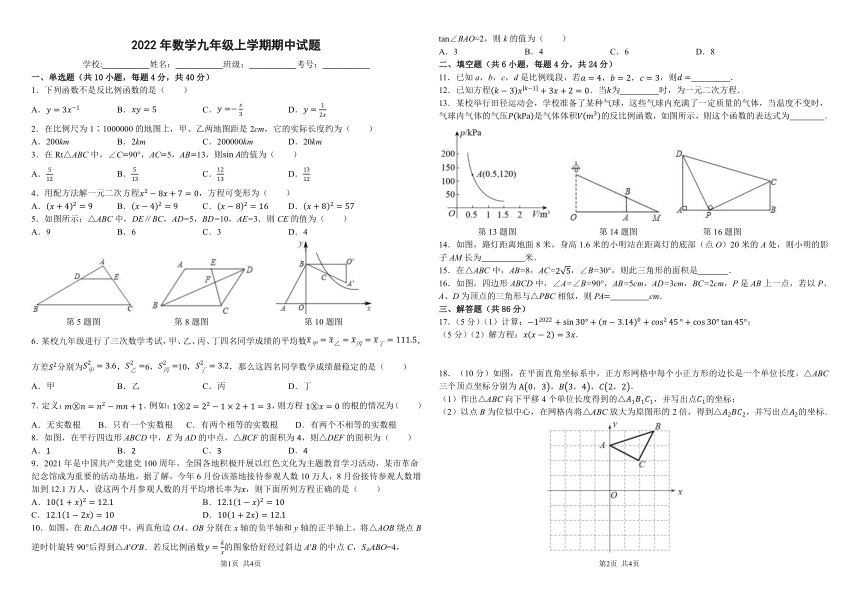
tan∠BAO=2,则 k的值为( )
2022 年数学九年级上学期期中试题 A.3 B.4 C.6 D.8
学校:___________姓名:___________班级:___________考号:___________ 二、填空题(共 6小题,每题 4 分,共 24 分)
一、单选题(共 10 小题,每题 4 分,共 40 分) 11.已知 a,b,c,d是比例线段,若 = 4, = 2, = 3,则 = .
1.下列函数不是反比例函数的是( ) 12.已知方程 3 1 + 3 + 2 = 0.当 为 时,为一元二次方程.
1 = 1 13.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,A. = 3 B. = 5 C. 3 D. = 2 气球内气体的气压 kPa 是气体体积 3 的反比例函数,如图所示,则这个函数的表达式为 .
2.在比例尺为 1∶1000000的地图上,甲、乙两地图距是 2cm,它的实际长度约为( )
A.200km B.2km C.200000km D.20km
3.在 Rt△ABC中,∠C=90°,AC=5,AB=13,则sin 的值为( )
A 5. B 5 C 12. . D 13.
12 13 13 12
4.用配方法解一元二次方程 2 8 + 7 = 0,方程可变形为( )
A. + 4 2 = 9 B. 4 2 = 9 C. 8 2 = 16 D. + 8 2 = 57
5.如图所示:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则 CE的值为( )
A.9 B.6 C.3 D.4 第 13题图 第 14题图 第 16题图
14.如图,路灯距离地面 8米,身高 1.6米的小明站在距离灯的底部(点 O)20米的 A处,则小明的影
子 AM长为 米.
15.在△ABC中,AB=8,AC=2 5,∠B=30°,则此三角形的面积是 .
16.如图,四边形 ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是 AB上一点,若以 P、
A、D为顶点的三角形与△PBC相似,则 PA= cm.
三、解答题(共 86 分)
第 5题图 第 8题图 第 10题图 17.(5分)(1)计算: 12022 + sin 30° + 3.14 0 + cos2 45 ° + cos 30° tan 45°;
= = = = 111.5 (5分)(2)解方程: 2 = 3 .6.某校九年级进行了三次数学考试,甲、乙、丙、丁四名同学成绩的平均数 甲 乙 丙 丁 ,
2 2 2 2
方差 2分别为 = 3.6, =6, =甲 乙 丙 10, = 3.2丁 ,那么这四名同学数学成绩最稳定的是( ) 18.(10分)如图,在平面直角坐标系中,正方形网格中每个小正方形的边长是一个单位长度,△ABC
A.甲 B.乙 C.丙 D.丁 三个顶点坐标分别为 A 0,3 , 3,4 , 2,2 .
(1)作出△ABC向下平移 4个单位长度得到的△ ,并写出点 的坐标;
7.定义: = 2 + 1.例如:1 2 = 22 1 × 2 + 1 = 3,则方程 1 = 0 1 1 1 1的根的情况为( )
(2)以点 B为位似中心,在网格内将△ABC放大为原图形的 2倍,得到△ 2 2,并写出点 2的坐标.
A.无实数根 B.只有一个实数根 C.有两个相等的实数根 D.有两个不相等的实数根
8.如图,在平行四边形 ABCD中,E为 AD的中点,△BCF的面积为 4,则△DEF的面积为( )
A.1 B.2 C.3 D.4
9.2021年是中国共产党建党 100周年,全国各地积极开展以红色文化为主题教育学习活动,某市革命
纪念馆成为重要的活动基地,据了解,今年 6月份该基地接待参观人数 10万人,8月份接待参观人数增
加到 12.1万人,设这两个月参观人数的月平均增长率为 ,则下面所列方程正确的是( )
A.10 1 + 2 = 12.1 B.12.1 1 2 = 10
C.12.1 1 2 = 10 D.10 1 + 2 = 12.1
10.如图,在 Rt△AOB中,两直角边 OA、OB分别在 x轴的负半轴和 y轴的正半轴上,将△AOB绕点 B
逆时针旋转 90°后得到△A′O′B = .若反比例函数 的图象恰好经过斜边 A′B的中点 C,S ABO=4,
△
第1页 共4页 第2页 共4页
19.(10分)如图所示,小明在家里楼顶上的点 A处,测量建在与小明家楼房同一水平线上相邻的电梯 22.(10分)如图,小华要为一个长 6分米,宽 4分米的长方形防疫科普电子小报四周添加一个边框,
楼的高,在点 A处看电梯楼顶部点 B处的仰角为 60°,在点 A处看这栋电梯楼底部点 C处的俯角为 45°, 要求边框的上下左右宽度相等,且边框面积与电子小报内容所占面积相等.求小华添加的边框的宽度.
若两栋楼之间的距离为 30m,求电梯楼的高 BC(结果保留根号).
23.(12分)阅读材料,解答问题:
材料 1 为了解方程 2 2 13 2 + 36 = 0,如果我们把 2看作一个整体,然后设 = 2,则原方程可化
20.(10分)如图,已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=4,BC=3,CE=6.
为 2 13 + 36 = 0,经过运算,原方程的解为 1,2 =± 2, 3,4 =± 3.我们把以上这种解决问题的方
(1)求∠B的度数;
(2)求 AD的长. 法通常叫做换元法.
材料 2 已知实数 , 满足 2 1 = 0, 2 1 = 0,且 ≠ ,显然 , 是方程 2 1 = 0
的两个不相等的实数根,由书达定理可知 + = 1, = 1.
根据上述材料,解决以下问题:
(1)直接应用:
方程 4 5 2 + 6 = 0 的解为 ;
(2)间接应用:
21.(10分)某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际, 已知实数 , 满足:2 4 7 2 + 1 = 0,2 4 7 2 + 1 = 0 且 ≠ ,求 4 + 4的值;
决定主要开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,
随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
24.(14分)如图,直线 = 1 +
与双曲线 = 2交于 A,B两点,已知点 A的坐标为 3,1 ,点 B
的坐标为 , 3 ,直线 AB与 轴交于点 C,与 轴交于点 D 0, 2 .
(1)求双曲线和直线 AB的解析式;
(2)若点 P是第二象限内反比例函数图象上的一点,△OCP
的面积是△ODB的面积的 3倍,求点 P的坐标;
(3)若点 E在 轴的负半轴上,是否存在以点 E,C,D为
顶点构成的三角形与△ODB相似?若存在,求出点 E的坐
(1)本次调查共有多少名学生喜欢篮球?并补全条形统计图; 标;若不存在,请说明理由.
(2)已知该校有 1200人,请根据样本估计全校最喜欢乒乓球的学生有多少名.
第3页 共4页 第4页 共4页
2022 年数学九年级上学期期中试题 A.3 B.4 C.6 D.8
学校:___________姓名:___________班级:___________考号:___________ 二、填空题(共 6小题,每题 4 分,共 24 分)
一、单选题(共 10 小题,每题 4 分,共 40 分) 11.已知 a,b,c,d是比例线段,若 = 4, = 2, = 3,则 = .
1.下列函数不是反比例函数的是( ) 12.已知方程 3 1 + 3 + 2 = 0.当 为 时,为一元二次方程.
1 = 1 13.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,A. = 3 B. = 5 C. 3 D. = 2 气球内气体的气压 kPa 是气体体积 3 的反比例函数,如图所示,则这个函数的表达式为 .
2.在比例尺为 1∶1000000的地图上,甲、乙两地图距是 2cm,它的实际长度约为( )
A.200km B.2km C.200000km D.20km
3.在 Rt△ABC中,∠C=90°,AC=5,AB=13,则sin 的值为( )
A 5. B 5 C 12. . D 13.
12 13 13 12
4.用配方法解一元二次方程 2 8 + 7 = 0,方程可变形为( )
A. + 4 2 = 9 B. 4 2 = 9 C. 8 2 = 16 D. + 8 2 = 57
5.如图所示:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则 CE的值为( )
A.9 B.6 C.3 D.4 第 13题图 第 14题图 第 16题图
14.如图,路灯距离地面 8米,身高 1.6米的小明站在距离灯的底部(点 O)20米的 A处,则小明的影
子 AM长为 米.
15.在△ABC中,AB=8,AC=2 5,∠B=30°,则此三角形的面积是 .
16.如图,四边形 ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是 AB上一点,若以 P、
A、D为顶点的三角形与△PBC相似,则 PA= cm.
三、解答题(共 86 分)
第 5题图 第 8题图 第 10题图 17.(5分)(1)计算: 12022 + sin 30° + 3.14 0 + cos2 45 ° + cos 30° tan 45°;
= = = = 111.5 (5分)(2)解方程: 2 = 3 .6.某校九年级进行了三次数学考试,甲、乙、丙、丁四名同学成绩的平均数 甲 乙 丙 丁 ,
2 2 2 2
方差 2分别为 = 3.6, =6, =甲 乙 丙 10, = 3.2丁 ,那么这四名同学数学成绩最稳定的是( ) 18.(10分)如图,在平面直角坐标系中,正方形网格中每个小正方形的边长是一个单位长度,△ABC
A.甲 B.乙 C.丙 D.丁 三个顶点坐标分别为 A 0,3 , 3,4 , 2,2 .
(1)作出△ABC向下平移 4个单位长度得到的△ ,并写出点 的坐标;
7.定义: = 2 + 1.例如:1 2 = 22 1 × 2 + 1 = 3,则方程 1 = 0 1 1 1 1的根的情况为( )
(2)以点 B为位似中心,在网格内将△ABC放大为原图形的 2倍,得到△ 2 2,并写出点 2的坐标.
A.无实数根 B.只有一个实数根 C.有两个相等的实数根 D.有两个不相等的实数根
8.如图,在平行四边形 ABCD中,E为 AD的中点,△BCF的面积为 4,则△DEF的面积为( )
A.1 B.2 C.3 D.4
9.2021年是中国共产党建党 100周年,全国各地积极开展以红色文化为主题教育学习活动,某市革命
纪念馆成为重要的活动基地,据了解,今年 6月份该基地接待参观人数 10万人,8月份接待参观人数增
加到 12.1万人,设这两个月参观人数的月平均增长率为 ,则下面所列方程正确的是( )
A.10 1 + 2 = 12.1 B.12.1 1 2 = 10
C.12.1 1 2 = 10 D.10 1 + 2 = 12.1
10.如图,在 Rt△AOB中,两直角边 OA、OB分别在 x轴的负半轴和 y轴的正半轴上,将△AOB绕点 B
逆时针旋转 90°后得到△A′O′B = .若反比例函数 的图象恰好经过斜边 A′B的中点 C,S ABO=4,
△
第1页 共4页 第2页 共4页
19.(10分)如图所示,小明在家里楼顶上的点 A处,测量建在与小明家楼房同一水平线上相邻的电梯 22.(10分)如图,小华要为一个长 6分米,宽 4分米的长方形防疫科普电子小报四周添加一个边框,
楼的高,在点 A处看电梯楼顶部点 B处的仰角为 60°,在点 A处看这栋电梯楼底部点 C处的俯角为 45°, 要求边框的上下左右宽度相等,且边框面积与电子小报内容所占面积相等.求小华添加的边框的宽度.
若两栋楼之间的距离为 30m,求电梯楼的高 BC(结果保留根号).
23.(12分)阅读材料,解答问题:
材料 1 为了解方程 2 2 13 2 + 36 = 0,如果我们把 2看作一个整体,然后设 = 2,则原方程可化
20.(10分)如图,已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=4,BC=3,CE=6.
为 2 13 + 36 = 0,经过运算,原方程的解为 1,2 =± 2, 3,4 =± 3.我们把以上这种解决问题的方
(1)求∠B的度数;
(2)求 AD的长. 法通常叫做换元法.
材料 2 已知实数 , 满足 2 1 = 0, 2 1 = 0,且 ≠ ,显然 , 是方程 2 1 = 0
的两个不相等的实数根,由书达定理可知 + = 1, = 1.
根据上述材料,解决以下问题:
(1)直接应用:
方程 4 5 2 + 6 = 0 的解为 ;
(2)间接应用:
21.(10分)某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际, 已知实数 , 满足:2 4 7 2 + 1 = 0,2 4 7 2 + 1 = 0 且 ≠ ,求 4 + 4的值;
决定主要开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,
随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
24.(14分)如图,直线 = 1 +
与双曲线 = 2交于 A,B两点,已知点 A的坐标为 3,1 ,点 B
的坐标为 , 3 ,直线 AB与 轴交于点 C,与 轴交于点 D 0, 2 .
(1)求双曲线和直线 AB的解析式;
(2)若点 P是第二象限内反比例函数图象上的一点,△OCP
的面积是△ODB的面积的 3倍,求点 P的坐标;
(3)若点 E在 轴的负半轴上,是否存在以点 E,C,D为
顶点构成的三角形与△ODB相似?若存在,求出点 E的坐
(1)本次调查共有多少名学生喜欢篮球?并补全条形统计图; 标;若不存在,请说明理由.
(2)已知该校有 1200人,请根据样本估计全校最喜欢乒乓球的学生有多少名.
第3页 共4页 第4页 共4页
同课章节目录
