5.4.2正弦函数、余弦函数的性质(第2课时)教学课件(共32张PPT)
文档属性
| 名称 | 5.4.2正弦函数、余弦函数的性质(第2课时)教学课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 07:48:43 | ||
图片预览










文档简介
(共32张PPT)
5.4.2正弦函数、余弦函数的性质
(第二课时)
第五章 三角函数
学习目标
1.理解正弦函数、余弦函数的单调性具有周期性变化规律,通过一个周期内的单调性进而研究在整个定义域上的性质.
2.能够利用单调性解决一些问题,比如比较大小,求最值等.
01
新课导入
新课导入
过山车是一项富有刺激性的娱乐工具,该运动包含了许多物理学原理,
人们在设计过山车时巧妙地运用了这些原理.如果能亲身体验一下过山车那感觉真是妙不可言.一个基本的过山车构造中,包含了爬升、滑落、倒转(儿童过山车没有倒转),几个循环路径.
新课导入
问题:(1)函数y=sin x与y=cos x也像过山车一样“爬升”,“滑落”,这是y=sin x,y=cos x的哪些性质?
(2)过山车爬升到最高点,然后滑落到最低点,然后再爬升,对应
y=sin x,y=cos x的哪些性质?y=sin x,y=cos x在什么位置取得最大(小)值?
余弦函数是否也具有上述特点?
02
探索新知
单调性
你还能举出一些这样的例子吗?
观察正弦函数 的图像
由于正弦函数是周期函数,我们可以先在它 一个周期区间(如
)上讨论它的单调性,再利用它的周期性,将单调性扩展到整个定义域.
问题1:函数值的变化有什么特点?
单调性
你还能举出一些这样的例子吗?
问题1:函数值的变化有什么特点?
单调性
问题2:推广到整个定义域呢?
单调性
你还能举出一些这样的例子吗?
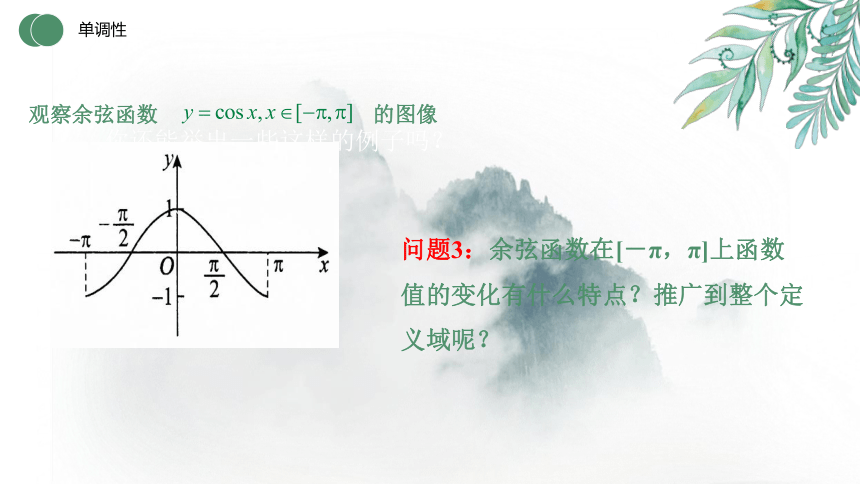
观察余弦函数 的图像
问题3:余弦函数在[-π,π]上函数值的变化有什么特点?推广到整个定义域呢?
单调性
你还能举出一些这样的例子吗?
问题3:余弦函数在[-π,π]上函数值的变化有什么特点?推广到整个定义域呢?
单调性
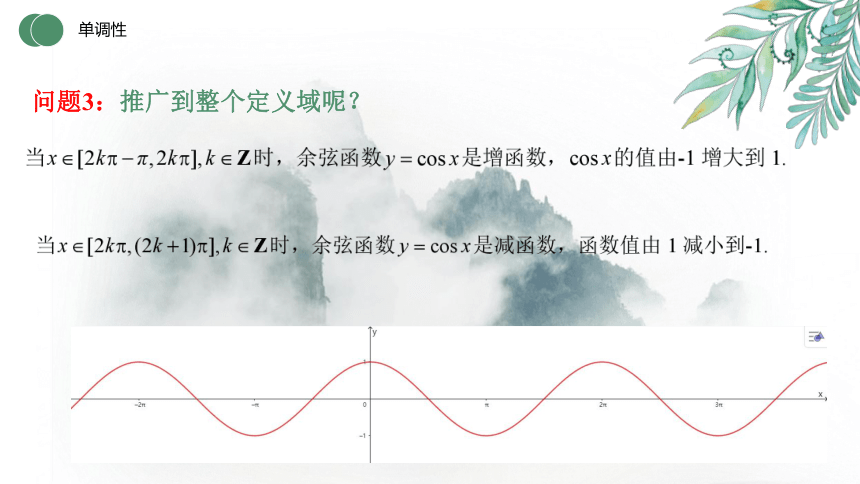
问题3:推广到整个定义域呢?
单调性
问题4:正弦函数、余弦函数的单调区间分别是什么?
最大值与最小值
你还能举出一些这样的例子吗?
问题5:继续观察图像,当正弦函数、余弦函数取最值时,
x的取值有何规律?
最大值与最小值
你还能举出一些这样的例子吗?
问题5:继续观察图像,当正弦函数、余弦函数取最值时,
x的取值有何规律?
例3
例3 下列函数有最大值、最小值吗?如果有,请写出最大值、最小值时自变量x的集合,并求出最大值、最小值.
例3
例3
方法总结:
(1)求解例题的基本依据是正弦函数、余弦函数的最大(小)值.
(3)余弦函数类似.
例4
例4 不通过求值,比较下列各组数的大小
分析:可利用三角函数的单调性比较两个同名三角函数值的大小.为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
例4
例4 不通过求值,比较下列各组数的大小
分析:可利用三角函数的单调性比较两个同名三角函数值的大小.为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
例4
方法总结:
比较三角函数值的大小时,先化三角函数为同名三角函数,再将角转化到同一个单调区间内,利用单调性比较大小.若α,β不在同一个单调区间内,则要通过诱导公式等工具先把α,β转化到同一个单调区间内再比较函数值的大小,有时可先大致判断函数值的符号,若符号不同,则大小易判.
例4
提问:你能借助单位圆直观地比较上述两对函数值的大小吗?试一试
例5
例5 求函数 的单调递增区间
思考
你能求出函数 的单调区间吗?
例4
方法技巧:
03
练习
练习1
B
练习2
D
04
小结
小结
[-1,1]
[-1,1]
小结
谢谢观看
XIEXIEGUANKAN
5.4.2正弦函数、余弦函数的性质
(第二课时)
第五章 三角函数
学习目标
1.理解正弦函数、余弦函数的单调性具有周期性变化规律,通过一个周期内的单调性进而研究在整个定义域上的性质.
2.能够利用单调性解决一些问题,比如比较大小,求最值等.
01
新课导入
新课导入
过山车是一项富有刺激性的娱乐工具,该运动包含了许多物理学原理,
人们在设计过山车时巧妙地运用了这些原理.如果能亲身体验一下过山车那感觉真是妙不可言.一个基本的过山车构造中,包含了爬升、滑落、倒转(儿童过山车没有倒转),几个循环路径.
新课导入
问题:(1)函数y=sin x与y=cos x也像过山车一样“爬升”,“滑落”,这是y=sin x,y=cos x的哪些性质?
(2)过山车爬升到最高点,然后滑落到最低点,然后再爬升,对应
y=sin x,y=cos x的哪些性质?y=sin x,y=cos x在什么位置取得最大(小)值?
余弦函数是否也具有上述特点?
02
探索新知
单调性
你还能举出一些这样的例子吗?
观察正弦函数 的图像
由于正弦函数是周期函数,我们可以先在它 一个周期区间(如
)上讨论它的单调性,再利用它的周期性,将单调性扩展到整个定义域.
问题1:函数值的变化有什么特点?
单调性
你还能举出一些这样的例子吗?
问题1:函数值的变化有什么特点?
单调性
问题2:推广到整个定义域呢?
单调性
你还能举出一些这样的例子吗?
观察余弦函数 的图像
问题3:余弦函数在[-π,π]上函数值的变化有什么特点?推广到整个定义域呢?
单调性
你还能举出一些这样的例子吗?
问题3:余弦函数在[-π,π]上函数值的变化有什么特点?推广到整个定义域呢?
单调性
问题3:推广到整个定义域呢?
单调性
问题4:正弦函数、余弦函数的单调区间分别是什么?
最大值与最小值
你还能举出一些这样的例子吗?
问题5:继续观察图像,当正弦函数、余弦函数取最值时,
x的取值有何规律?
最大值与最小值
你还能举出一些这样的例子吗?
问题5:继续观察图像,当正弦函数、余弦函数取最值时,
x的取值有何规律?
例3
例3 下列函数有最大值、最小值吗?如果有,请写出最大值、最小值时自变量x的集合,并求出最大值、最小值.
例3
例3
方法总结:
(1)求解例题的基本依据是正弦函数、余弦函数的最大(小)值.
(3)余弦函数类似.
例4
例4 不通过求值,比较下列各组数的大小
分析:可利用三角函数的单调性比较两个同名三角函数值的大小.为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
例4
例4 不通过求值,比较下列各组数的大小
分析:可利用三角函数的单调性比较两个同名三角函数值的大小.为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
例4
方法总结:
比较三角函数值的大小时,先化三角函数为同名三角函数,再将角转化到同一个单调区间内,利用单调性比较大小.若α,β不在同一个单调区间内,则要通过诱导公式等工具先把α,β转化到同一个单调区间内再比较函数值的大小,有时可先大致判断函数值的符号,若符号不同,则大小易判.
例4
提问:你能借助单位圆直观地比较上述两对函数值的大小吗?试一试
例5
例5 求函数 的单调递增区间
思考
你能求出函数 的单调区间吗?
例4
方法技巧:
03
练习
练习1
B
练习2
D
04
小结
小结
[-1,1]
[-1,1]
小结
谢谢观看
XIEXIEGUANKAN
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
