四川省成都市金苹果锦城第一中学2022-2023学年高三上学期期中考试数学(理)试题(含答案)
文档属性
| 名称 | 四川省成都市金苹果锦城第一中学2022-2023学年高三上学期期中考试数学(理)试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 522.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览




文档简介
成都金苹果锦城一中2022—2023学年(上)高2020级期中考试
数学(理科)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
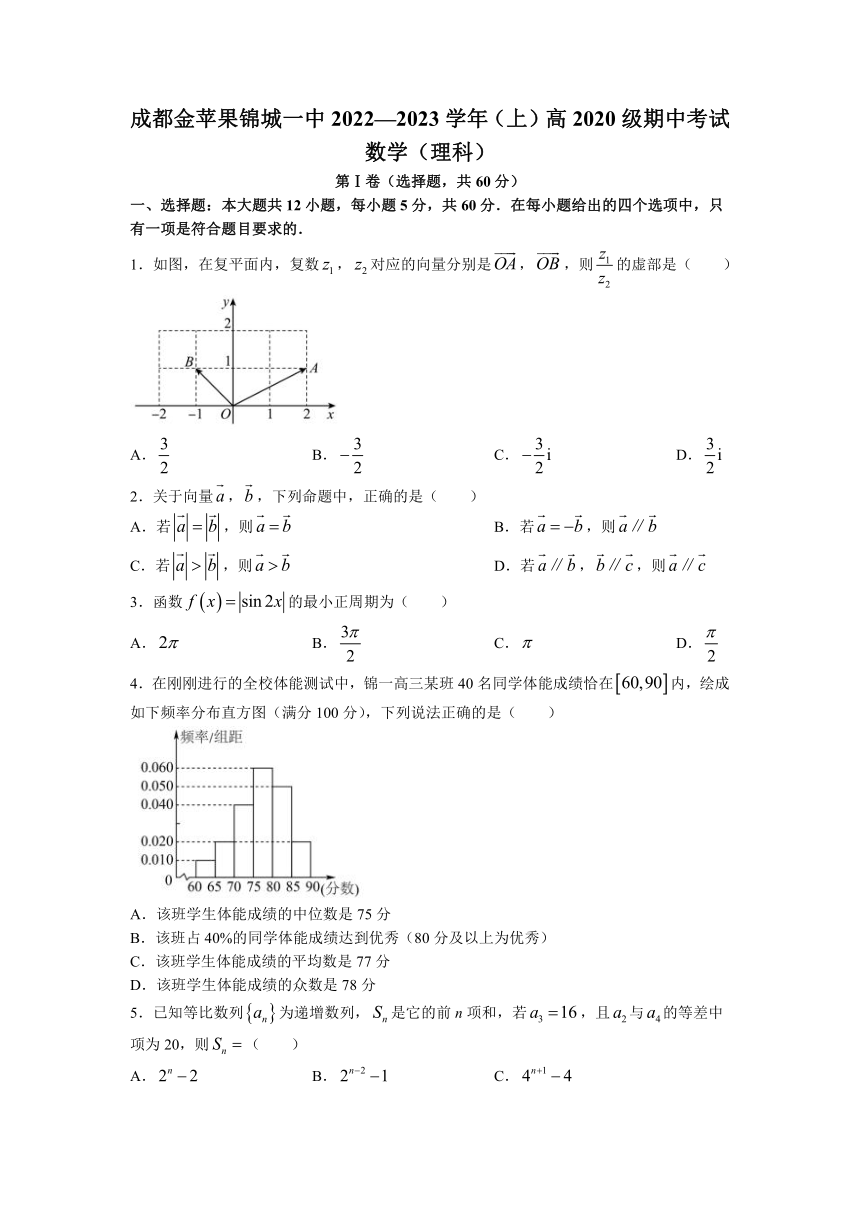
1.如图,在复平面内,复数,对应的向量分别是,,则的虚部是( )
A. B. C. D.
2.关于向量,,下列命题中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,,则
3.函数的最小正周期为( )
A. B. C. D.
4.在刚刚进行的全校体能测试中,锦一高三某班40名同学体能成绩恰在内,绘成如下频率分布直方图(满分100分),下列说法正确的是( )
A.该班学生体能成绩的中位数是75分
B.该班占40%的同学体能成绩达到优秀(80分及以上为优秀)
C.该班学生体能成绩的平均数是77分
D.该班学生体能成绩的众数是78分
5.已知等比数列为递增数列,是它的前n项和,若,且与的等差中项为20,则( )
A. B. C. D.
6.已知,则( )
A. B. C. D.
7.已知展开式各项的二项式系数之和为512,则展开式中的常数项是( )
A.84 B.-84 C.126 D.-126
8.定义在R上的奇函数满足,若当时,,则( )
A.-9 B.9 C.-3 D.3
9.已知数列的前n项和为,,且,则下列说法中错误的是( )
A. B.
C.是等比数列 D.是等比数列
10.把函数的图象向左平移个单位,再将得到的曲线上所有点的横坐标变为原来的倍,纵坐标不变,得到函数的图象.若函数在上恰有3个零点,则的取值范围是( )
A. B. C. D.
11.已知函数,且,,,则a,b,c的大小关系为( )
A. B. C. D.
12.已知定义域为R的奇函数满足:当时,;当时,.现有下列四个结论:
①既无最大值也无最小值;②当时,;
③若,,则;④若方程在上恰有三个根,则实数k的取值范围是.其中所有正确结论的个数是( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.
13.已知向量,满足,,,则______.
14.记为等差数列的前n项和,若,则______.
15.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=200m,则山高MN=______m.
16.关于x的不等式恒成立,则实数a的取值范围是______.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本题12分)
在①;②;③这三个条件中任选一个,解答下面两个问题.
(1)求角A;
(2)在△ABC中,内角A,B,C的对边分别是a,b,,若已知,,求b,c的值.
18.(本题12分)
为保护学生视力,让学生在学校专心学习,促进学生身心健康发展,教育部于2021年1月15日下发文件《关于加强中小学生手机管理工作的通知》,即对中小学生的手机使用和管理作出了相关的规定.某中学研究型学习小组调查研究“中学生每日使用手机的时间”.从该校学生中随机选取了100名学生,其中男生80人,女生20人,调查得到如表所示的统计数据.
时间t/min
人数 32 28 14 14 8 4
(1)若每日使用手机的时间小于36min表现为“正常”,大于等于36min表现为“手机成瘾”,请根据已知条件补全下列2×2列联表,并判断是否有99%把握认为“手机成瘾”与性别有关;
“正常” “手机成瘾” 合计
男生 80
女生 10 20
合计 100
(2)以频率估计概率,若在该校学生中随机挑选3人,记这3人每日使用手机的时间在的人数为随机变量X,求X的分布列和数学期望.
附:,.
0.10 0.05 0.025 0.01 0.005
2.706 3.841 5.024 6.635 7.879
19.(本题12分)
如图,在正三棱柱(底面为正三角形的直棱柱)中,,D为BC的中点,E为侧棱上的点.
(1)当E为的中点时,求证:平面;
(2)是否存在点E,使得平面与平面ABC所成的锐二面角为60°,若存在,求AE的长,若不存在,说明理由.
20.(本题12分)
如图,已知椭圆的左、右两个焦点分别为、,左、右顶点分别为A、B,离心率为,过的动直线l与椭圆C交于M、N两点,且的周长为8.
(1)求椭圆C的标准方程;
(2)点P为x轴上一点,使得∠MPO=∠NPO(O为坐标原点)恒成立,记、的面积记分别为、,求的取值范围.
21.(本题12分)
已知函数,.
(1)讨论函数的单调性;
(2)当时,设,,函数有两个极值点,.
①求m的取值范围;
②若,求的取值范围.
(二)选考题,共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
[选修4-4:坐标系与参数方程]
22.已知曲线,A是曲线上的动点,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,以极点O为中心,将点A绕点O逆时针旋转90°得到点B,设点B的轨迹方程为曲线.
(1)求曲线,的极坐标方程;
(2)在极坐标系中,定点,射线与曲线,分别交于异于极点O的M,N两点,求△PMN的面积.
[选修4-5:不等式选讲]
23.已知函数的最小值为m.
(1)求m;
(2)已知a,b,c为正数,且,求的最小值.
高三上期半期考试理科数学参考答案
选择题 BBDCD CBCCB DC
填空题 13.1 14.14 15.300 16.
三、解大题
17. (1)若选①:由已知得:
,由正弦定理可得
,可得,
由余弦定理可得, 因为, 所以.
若选②:因为,
由正弦定理可得,
所以
因为 , 所以, 所以,
因为, 所以
若选③:因为 ,由正弦定理得,
因为 ,所以,故可得
即,所以,因为 ,所以;
(2)由(1)可得,,所以,
由余弦定理得:,
所以,又因为,解得,.
18.(1)
“正常” “手机成瘾” 合计
男生 64 16 80
女生 10 10 20
合计 74 26 100
所以有99%把握认为“手机成瘾”与性别有关.
(2) 由题可得学生每日使用手机的时间在内的概率为,
则,所以, ,
, ,
所以的分布列为:
0 1 2 3
所以.
19. (1)取中点,连接,,为的中点,
所以,且,又因为为的中点,,
且,所以,且,所以,且,
所以四边形为平行四边形,所以,因为平面,
平面,所以平面.
(2)如图建立空间直角坐标系,
所以,,设,
,,
设平面的一个法向量,
所以,所以,
所以,
平面的一个法向量为,
所以,整理得
,所以,所以,
所以不存在点,使得平面与平面所成的锐二面角为.
20. (1),解得,,,
所以椭圆C的标准方程为.
(2)设点 使得恒成立
设直线MN:,点、,则,
由消去并整理得:,
则,,
因为,则直线的斜率满足,
而 ,恒成立,解得,
,设,有,于是得,
因此有,,
,显然,当且仅当时取等号,
因此,解得,则,
所以的取值范围是.
21.(1)
当时,的增区间是,,减区间是
当时,在上单调递增;
当时,的增区间是,,减区间是;
(2)①,因为函数有两个极值点
所以有两个变号零点;
当时,,单减
当时,,单增
当时,;当时,
所以只需
所以;
②由已知
,令 得
,
令,,则,
令,则
单增,又因为
所以当时,,,单增
由洛必达法则 ,
所以,所求范围是2,
22. (1)曲线C1:x2+(y-2)2=4,即x2+y2-4y=0.
从而ρ2=4ρsin θ.
所以曲线C1的极坐标方程为ρ=6sin θ.
设B(ρ,θ),则A,
则有ρ=4sin=-4cos θ.
所以曲线C2的极坐标方程为ρ=-4cos θ.
(2)P到射线θ=(ρ>0)的距离为d=4sin=2,
射线θ=(ρ>0)与曲线C1的交点M,则,=4sin =2,
射线θ=(ρ>0)与曲线C2的交点N,则,=-4cos =,
则|MN|==,则==.
23. (1)依题意得:,
当时,,
当时,,
当时,,
综上,当时,取得最小值1,即的最小值.
(2)解:由(1)知,,
(当且仅当时等号成立),
∴,
当且仅当,即,时等号成立,
∴的最小值为12.
数学(理科)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,在复平面内,复数,对应的向量分别是,,则的虚部是( )
A. B. C. D.
2.关于向量,,下列命题中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,,则
3.函数的最小正周期为( )
A. B. C. D.
4.在刚刚进行的全校体能测试中,锦一高三某班40名同学体能成绩恰在内,绘成如下频率分布直方图(满分100分),下列说法正确的是( )
A.该班学生体能成绩的中位数是75分
B.该班占40%的同学体能成绩达到优秀(80分及以上为优秀)
C.该班学生体能成绩的平均数是77分
D.该班学生体能成绩的众数是78分
5.已知等比数列为递增数列,是它的前n项和,若,且与的等差中项为20,则( )
A. B. C. D.
6.已知,则( )
A. B. C. D.
7.已知展开式各项的二项式系数之和为512,则展开式中的常数项是( )
A.84 B.-84 C.126 D.-126
8.定义在R上的奇函数满足,若当时,,则( )
A.-9 B.9 C.-3 D.3
9.已知数列的前n项和为,,且,则下列说法中错误的是( )
A. B.
C.是等比数列 D.是等比数列
10.把函数的图象向左平移个单位,再将得到的曲线上所有点的横坐标变为原来的倍,纵坐标不变,得到函数的图象.若函数在上恰有3个零点,则的取值范围是( )
A. B. C. D.
11.已知函数,且,,,则a,b,c的大小关系为( )
A. B. C. D.
12.已知定义域为R的奇函数满足:当时,;当时,.现有下列四个结论:
①既无最大值也无最小值;②当时,;
③若,,则;④若方程在上恰有三个根,则实数k的取值范围是.其中所有正确结论的个数是( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.
13.已知向量,满足,,,则______.
14.记为等差数列的前n项和,若,则______.
15.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=200m,则山高MN=______m.
16.关于x的不等式恒成立,则实数a的取值范围是______.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本题12分)
在①;②;③这三个条件中任选一个,解答下面两个问题.
(1)求角A;
(2)在△ABC中,内角A,B,C的对边分别是a,b,,若已知,,求b,c的值.
18.(本题12分)
为保护学生视力,让学生在学校专心学习,促进学生身心健康发展,教育部于2021年1月15日下发文件《关于加强中小学生手机管理工作的通知》,即对中小学生的手机使用和管理作出了相关的规定.某中学研究型学习小组调查研究“中学生每日使用手机的时间”.从该校学生中随机选取了100名学生,其中男生80人,女生20人,调查得到如表所示的统计数据.
时间t/min
人数 32 28 14 14 8 4
(1)若每日使用手机的时间小于36min表现为“正常”,大于等于36min表现为“手机成瘾”,请根据已知条件补全下列2×2列联表,并判断是否有99%把握认为“手机成瘾”与性别有关;
“正常” “手机成瘾” 合计
男生 80
女生 10 20
合计 100
(2)以频率估计概率,若在该校学生中随机挑选3人,记这3人每日使用手机的时间在的人数为随机变量X,求X的分布列和数学期望.
附:,.
0.10 0.05 0.025 0.01 0.005
2.706 3.841 5.024 6.635 7.879
19.(本题12分)
如图,在正三棱柱(底面为正三角形的直棱柱)中,,D为BC的中点,E为侧棱上的点.
(1)当E为的中点时,求证:平面;
(2)是否存在点E,使得平面与平面ABC所成的锐二面角为60°,若存在,求AE的长,若不存在,说明理由.
20.(本题12分)
如图,已知椭圆的左、右两个焦点分别为、,左、右顶点分别为A、B,离心率为,过的动直线l与椭圆C交于M、N两点,且的周长为8.
(1)求椭圆C的标准方程;
(2)点P为x轴上一点,使得∠MPO=∠NPO(O为坐标原点)恒成立,记、的面积记分别为、,求的取值范围.
21.(本题12分)
已知函数,.
(1)讨论函数的单调性;
(2)当时,设,,函数有两个极值点,.
①求m的取值范围;
②若,求的取值范围.
(二)选考题,共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
[选修4-4:坐标系与参数方程]
22.已知曲线,A是曲线上的动点,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,以极点O为中心,将点A绕点O逆时针旋转90°得到点B,设点B的轨迹方程为曲线.
(1)求曲线,的极坐标方程;
(2)在极坐标系中,定点,射线与曲线,分别交于异于极点O的M,N两点,求△PMN的面积.
[选修4-5:不等式选讲]
23.已知函数的最小值为m.
(1)求m;
(2)已知a,b,c为正数,且,求的最小值.
高三上期半期考试理科数学参考答案
选择题 BBDCD CBCCB DC
填空题 13.1 14.14 15.300 16.
三、解大题
17. (1)若选①:由已知得:
,由正弦定理可得
,可得,
由余弦定理可得, 因为, 所以.
若选②:因为,
由正弦定理可得,
所以
因为 , 所以, 所以,
因为, 所以
若选③:因为 ,由正弦定理得,
因为 ,所以,故可得
即,所以,因为 ,所以;
(2)由(1)可得,,所以,
由余弦定理得:,
所以,又因为,解得,.
18.(1)
“正常” “手机成瘾” 合计
男生 64 16 80
女生 10 10 20
合计 74 26 100
所以有99%把握认为“手机成瘾”与性别有关.
(2) 由题可得学生每日使用手机的时间在内的概率为,
则,所以, ,
, ,
所以的分布列为:
0 1 2 3
所以.
19. (1)取中点,连接,,为的中点,
所以,且,又因为为的中点,,
且,所以,且,所以,且,
所以四边形为平行四边形,所以,因为平面,
平面,所以平面.
(2)如图建立空间直角坐标系,
所以,,设,
,,
设平面的一个法向量,
所以,所以,
所以,
平面的一个法向量为,
所以,整理得
,所以,所以,
所以不存在点,使得平面与平面所成的锐二面角为.
20. (1),解得,,,
所以椭圆C的标准方程为.
(2)设点 使得恒成立
设直线MN:,点、,则,
由消去并整理得:,
则,,
因为,则直线的斜率满足,
而 ,恒成立,解得,
,设,有,于是得,
因此有,,
,显然,当且仅当时取等号,
因此,解得,则,
所以的取值范围是.
21.(1)
当时,的增区间是,,减区间是
当时,在上单调递增;
当时,的增区间是,,减区间是;
(2)①,因为函数有两个极值点
所以有两个变号零点;
当时,,单减
当时,,单增
当时,;当时,
所以只需
所以;
②由已知
,令 得
,
令,,则,
令,则
单增,又因为
所以当时,,,单增
由洛必达法则 ,
所以,所求范围是2,
22. (1)曲线C1:x2+(y-2)2=4,即x2+y2-4y=0.
从而ρ2=4ρsin θ.
所以曲线C1的极坐标方程为ρ=6sin θ.
设B(ρ,θ),则A,
则有ρ=4sin=-4cos θ.
所以曲线C2的极坐标方程为ρ=-4cos θ.
(2)P到射线θ=(ρ>0)的距离为d=4sin=2,
射线θ=(ρ>0)与曲线C1的交点M,则,=4sin =2,
射线θ=(ρ>0)与曲线C2的交点N,则,=-4cos =,
则|MN|==,则==.
23. (1)依题意得:,
当时,,
当时,,
当时,,
综上,当时,取得最小值1,即的最小值.
(2)解:由(1)知,,
(当且仅当时等号成立),
∴,
当且仅当,即,时等号成立,
∴的最小值为12.
同课章节目录
