4.5.1函数的零点与方程的解 课件(共17张PPT)
文档属性
| 名称 | 4.5.1函数的零点与方程的解 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 08:02:00 | ||
图片预览



文档简介
(共17张PPT)
4.5.1函数的零点与方程的解
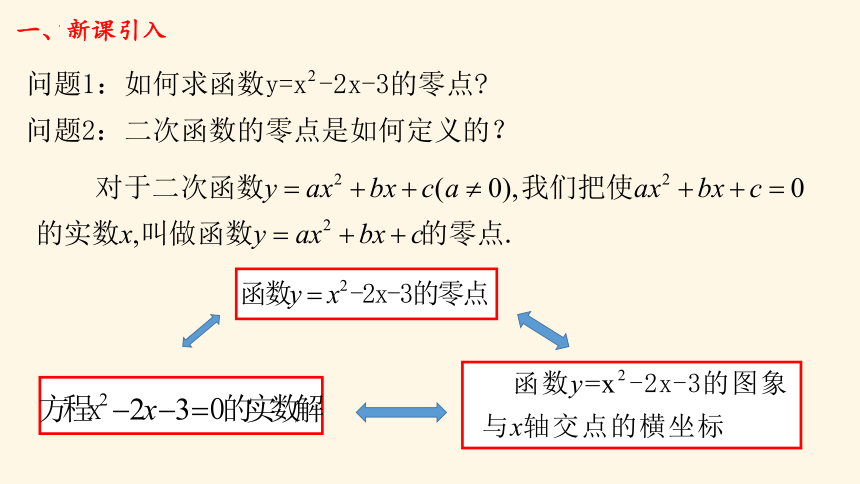
一、新课引入
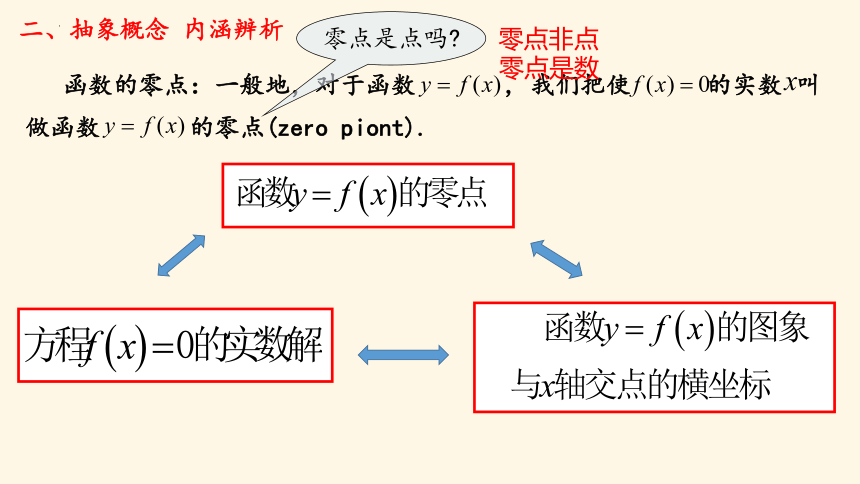
二、抽象概念 内涵辨析
函数的零点:一般地,对于函数 , 我们把使 的实数 叫做函数 的零点(zero piont).
零点是点吗
零点非点
零点是数
三、习题练习 巩固新知
问题1.像 这种不能直接求方程的解,那用什么方法来判断方程是否有解?若有,有几个?
求下列函数的零点或方程的根。
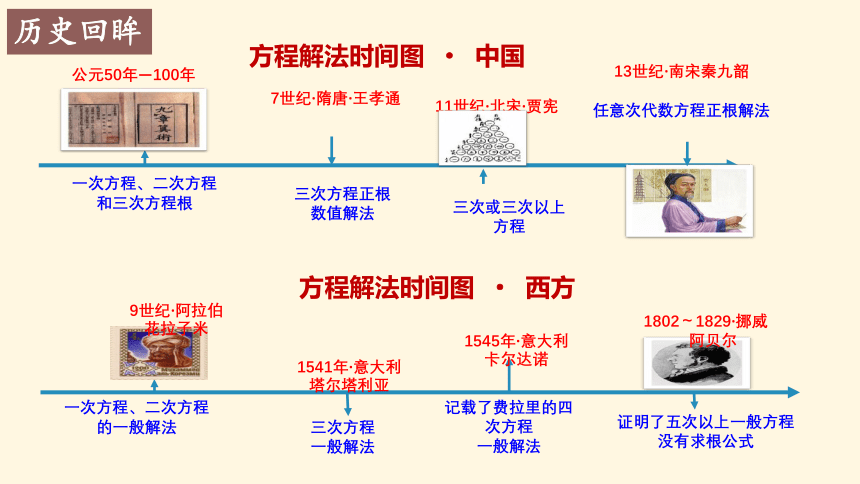
方程解法时间图 · 中国
公元50年—100年
一次方程、二次方程
和三次方程根
11世纪·北宋·贾宪
三次或三次以上
方程
三次方程正根
数值解法
7世纪·隋唐·王孝通
13世纪·南宋秦九韶
任意次代数方程正根解法
历史回眸
方程解法时间图 · 西方
一次方程、二次方程
的一般解法
1541年·意大利
塔尔塔利亚
三次方程
一般解法
1802~1829·挪威
阿贝尔
证明了五次以上一般方程
没有求根公式
记载了费拉里的四次方程
一般解法
9世纪·阿拉伯
花拉子米
1545年·意大利
卡尔达诺
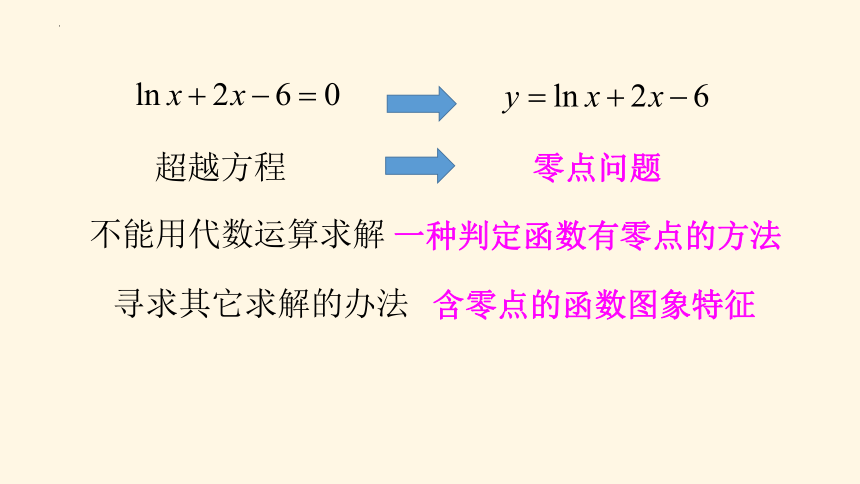
零点问题
含零点的函数图象特征
一种判定函数有零点的方法
2
1
1
-2
2
-1
3
4
-1
-2
-3
-4
0
y
x
四、小组讨论 合作探究:
请同学们先独立思考下列问题,然后小组讨论,形成结论,汇报结果.
如果函数 y=f(x) 在区间[a,b]上的图象是一条连续不断的曲线,且有 f(a) f(b)<0 ,那么函数 y=f(x)在区间 (a,b) 内至少有一个零点,即存在 c ∈ (a,b),使得 f(c) =0,这个c也就是方程 f(x)=0 的解。
函数零点存在定理
新知探究
捷克数学家伯纳德·波尔查诺于1817年证明了这个定理,同时证明了这个定理的一般情况(即介值定理)
a
b
如果函数 y=f(x) 在区间[a,b]上的图象是一条连续不断的曲线,且有 f(a) f(b)<0 ,那么函数 y=f(x)在区间 (a,b) 内至少有一个零点,即存在 c ∈ (a,b),使得 f(c) =0,这个c也就是方程 f(x)=0 的解。
函数零点存在定理
思考3:若将条件与结论互换,还成立吗?
思考4:定理中,增加一个什么条件,能使零点有唯一性呢?
新知探究
(定理推论)
是
的什么条件
充分不必要
思考1:若将定理中“连续不断的曲线”删去,还成立吗?
思考2:若将定理中“f(a) f(b)<0”删去呢?
函数零点存在定理的推论
练习5 已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:
x 1 2 3 4 5 6 7
f(x) 23 9 –7 11 –5 –12 –26
那么函数在区间[1,6]上的零点至少有( )个
A 5 B 4 C 3 D 2
C
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
六、例题练习 巩固新知
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
易证f(x)=lnx+2x-6在(0,+∞)上是增函数,
所以函数在定义域(0,+∞)内仅有一个零点.
六、例题练习 巩固新知
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
易证f(x)=lnx+2x-6在(0,+∞)上是增函数,
所以函数在定义域(0,+∞)内仅有一个零点.
变式:
求方程lnx+x2-6=0的实数解个数.
六、例题练习 巩固新知
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
易证f(x)=lnx+2x-6在(0,+∞)上是增函数,
所以函数在定义域(0,+∞)内仅有一个零点.
变式:
求方程lnx+x2-6=0的实数解个数.
六、例题练习 巩固新知
变式:
求函数 的零点个数.
小结提升 形成结构:
函数的零点
方程的解
函数图象的公共点
函数零点
存在定理
数形结合思想
函数与方程思想
转化与化归思想
连续曲线,
布置作业 应用迁移 教科书习题4.5第3、7、13题,作业本
拓广探索
必修1第156页第13题
4.5.1函数的零点与方程的解
一、新课引入
二、抽象概念 内涵辨析
函数的零点:一般地,对于函数 , 我们把使 的实数 叫做函数 的零点(zero piont).
零点是点吗
零点非点
零点是数
三、习题练习 巩固新知
问题1.像 这种不能直接求方程的解,那用什么方法来判断方程是否有解?若有,有几个?
求下列函数的零点或方程的根。
方程解法时间图 · 中国
公元50年—100年
一次方程、二次方程
和三次方程根
11世纪·北宋·贾宪
三次或三次以上
方程
三次方程正根
数值解法
7世纪·隋唐·王孝通
13世纪·南宋秦九韶
任意次代数方程正根解法
历史回眸
方程解法时间图 · 西方
一次方程、二次方程
的一般解法
1541年·意大利
塔尔塔利亚
三次方程
一般解法
1802~1829·挪威
阿贝尔
证明了五次以上一般方程
没有求根公式
记载了费拉里的四次方程
一般解法
9世纪·阿拉伯
花拉子米
1545年·意大利
卡尔达诺
零点问题
含零点的函数图象特征
一种判定函数有零点的方法
2
1
1
-2
2
-1
3
4
-1
-2
-3
-4
0
y
x
四、小组讨论 合作探究:
请同学们先独立思考下列问题,然后小组讨论,形成结论,汇报结果.
如果函数 y=f(x) 在区间[a,b]上的图象是一条连续不断的曲线,且有 f(a) f(b)<0 ,那么函数 y=f(x)在区间 (a,b) 内至少有一个零点,即存在 c ∈ (a,b),使得 f(c) =0,这个c也就是方程 f(x)=0 的解。
函数零点存在定理
新知探究
捷克数学家伯纳德·波尔查诺于1817年证明了这个定理,同时证明了这个定理的一般情况(即介值定理)
a
b
如果函数 y=f(x) 在区间[a,b]上的图象是一条连续不断的曲线,且有 f(a) f(b)<0 ,那么函数 y=f(x)在区间 (a,b) 内至少有一个零点,即存在 c ∈ (a,b),使得 f(c) =0,这个c也就是方程 f(x)=0 的解。
函数零点存在定理
思考3:若将条件与结论互换,还成立吗?
思考4:定理中,增加一个什么条件,能使零点有唯一性呢?
新知探究
(定理推论)
是
的什么条件
充分不必要
思考1:若将定理中“连续不断的曲线”删去,还成立吗?
思考2:若将定理中“f(a) f(b)<0”删去呢?
函数零点存在定理的推论
练习5 已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:
x 1 2 3 4 5 6 7
f(x) 23 9 –7 11 –5 –12 –26
那么函数在区间[1,6]上的零点至少有( )个
A 5 B 4 C 3 D 2
C
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
六、例题练习 巩固新知
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
易证f(x)=lnx+2x-6在(0,+∞)上是增函数,
所以函数在定义域(0,+∞)内仅有一个零点.
六、例题练习 巩固新知
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
易证f(x)=lnx+2x-6在(0,+∞)上是增函数,
所以函数在定义域(0,+∞)内仅有一个零点.
变式:
求方程lnx+x2-6=0的实数解个数.
六、例题练习 巩固新知
例1 求方程lnx+2x-6=0的实数解个数.
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
易证f(x)=lnx+2x-6在(0,+∞)上是增函数,
所以函数在定义域(0,+∞)内仅有一个零点.
变式:
求方程lnx+x2-6=0的实数解个数.
六、例题练习 巩固新知
变式:
求函数 的零点个数.
小结提升 形成结构:
函数的零点
方程的解
函数图象的公共点
函数零点
存在定理
数形结合思想
函数与方程思想
转化与化归思想
连续曲线,
布置作业 应用迁移 教科书习题4.5第3、7、13题,作业本
拓广探索
必修1第156页第13题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
