5.3诱导公式(第一课时) 课件(共28张PPT)
文档属性
| 名称 | 5.3诱导公式(第一课时) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 08:08:28 | ||
图片预览





文档简介
(共28张PPT)
5.3诱导公式
第一课时 诱导公式二—四
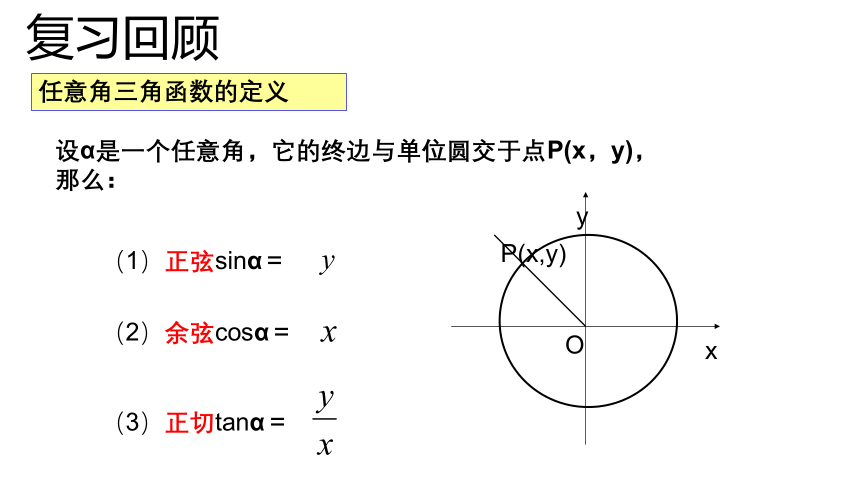
任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
x
y
O
P(x,y)
诱导公式(一)
实质:终边相同,三角函数值相等
用途:“大”角化“小”角
y
α的终边
x
o
π+α的终边
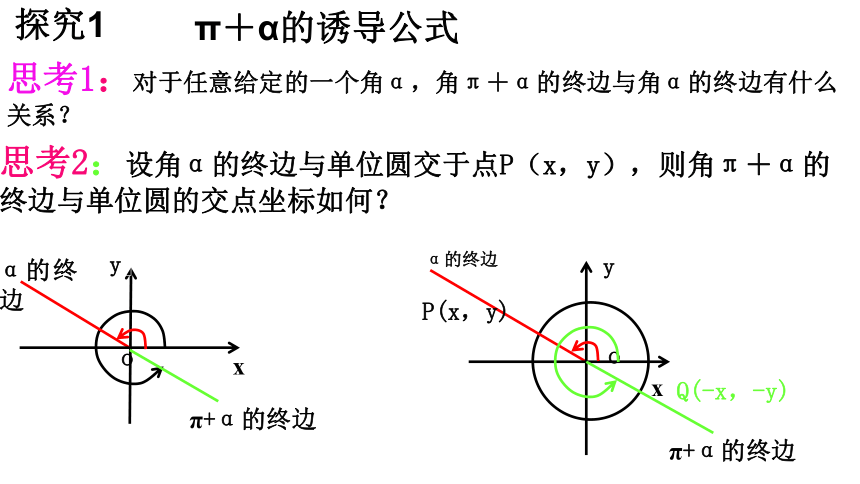
思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?
探究1
π+α的诱导公式
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?
α的终边
x
y
o
P(x,y)
π+α的终边
Q(-x,-y)
公式二
形如 的三角函数值与 的三角函数值之间的关系
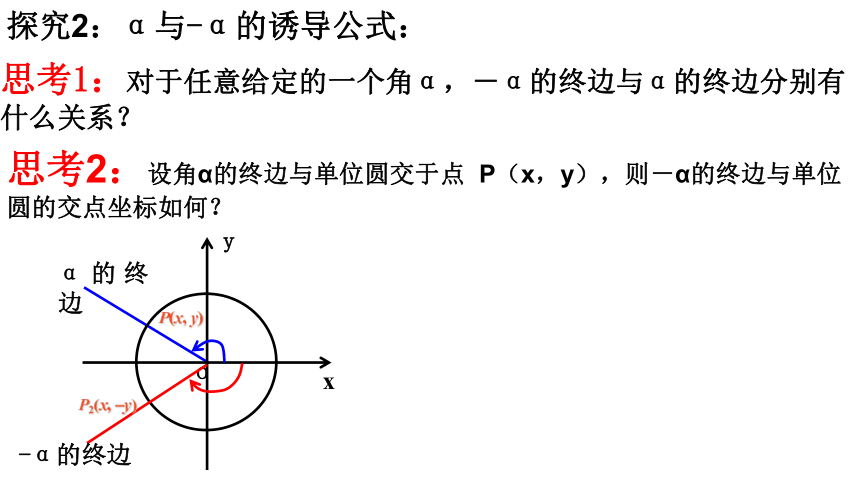
探究2:α与-α的诱导公式:
思考1:对于任意给定的一个角α,-α的终边与α的终边分别有什么关系?
思考2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?
y
α的终边
x
o
-α的终边
P(x, y)
P2(x, -y)
公式三
我们再来研究角 与 的三角函数值之间的关系
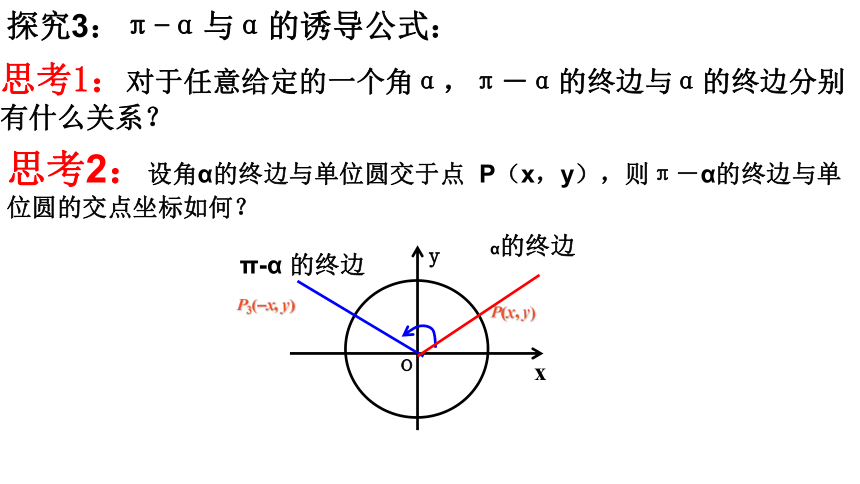
探究3:π-α与α的诱导公式:
思考1:对于任意给定的一个角α,π-α的终边与α的终边分别有什么关系?
思考2:设角α的终边与单位圆交于点 P(x,y),则π-α的终边与单位圆的交点坐标如何?
y
x
o
α的终边
π-α 的终边
P(x, y)
P3(-x, y)
公式四
(公式一)
(公式二)
(公式三)
(公式四)
三角函数的诱导公式一---四
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系.
归纳:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
简记作:“函数名不变,符号看象限”
题型一 给角求值问题
[解] (1)sin(-1200°)
=-sin1200°
=-sin(3×360°+120°)
=-sin120
=-sin(180°-60°)
(2)tan945°=tan(2×360°+225°)
=tan225°
=tan(180°+45°)
=tan45°=1.
利用诱导公式解决给角求值问题的步骤
答案
解 (1)原式=sin(120°-4×360°)cos(30°+3×360°)+cos(60°-3×360°)sin(30°+2×360°)+tan(135°+360°)
=sin120°cos30°+cos60°sin30°+tan135°
题型二 给值求值问题
解决条件求值问题的策略
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
答案
解析 (1)∵cos(α+β)=-1,
∴α+β=π+2kπ,k∈Z,
∴sin(α+2β)=sin[(α+β)+β]
=sin(π+β)
题型三 三角函数式的化简
三角函数式化简的常用方法
(1)依据所给式子合理选用诱导公式将所给角的三角函数转化为另一个角的三角函数
.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
(3)注意“1”的应用:1=sin2α+cos2α=tan.
(4)用诱导公式进行化简时,若遇到kπ±α的形式,需对k进行分类讨论,然后再运用诱导公式进行化简.
课堂小结:通过这节课我学会了什么?还有哪些疑惑?
1.三角函数的四组诱导公式;
2.三角函数诱导公式的应用(求值、化简);
3.三角函数诱导公式的记忆方法。( ? )
一、基本内容:
二、思想方法:
1.数形结合
2.转化与化归
利用诱导公式一~四,可以求任意角的三角函数,其基本思路(步骤)是:
这是一种化归与转化的数学思想.
任意负角的
三角函数
任意正角的
三角函数
0~2π的角
的三角函数
锐角的三角
函数
用公式三或一
用公式一
用公式
二或四
负化正,大化小,化到锐角就终了
未知
已知
作业:
练习:1,2
5.3诱导公式
第一课时 诱导公式二—四
任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
x
y
O
P(x,y)
诱导公式(一)
实质:终边相同,三角函数值相等
用途:“大”角化“小”角
y
α的终边
x
o
π+α的终边
思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?
探究1
π+α的诱导公式
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?
α的终边
x
y
o
P(x,y)
π+α的终边
Q(-x,-y)
公式二
形如 的三角函数值与 的三角函数值之间的关系
探究2:α与-α的诱导公式:
思考1:对于任意给定的一个角α,-α的终边与α的终边分别有什么关系?
思考2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?
y
α的终边
x
o
-α的终边
P(x, y)
P2(x, -y)
公式三
我们再来研究角 与 的三角函数值之间的关系
探究3:π-α与α的诱导公式:
思考1:对于任意给定的一个角α,π-α的终边与α的终边分别有什么关系?
思考2:设角α的终边与单位圆交于点 P(x,y),则π-α的终边与单位圆的交点坐标如何?
y
x
o
α的终边
π-α 的终边
P(x, y)
P3(-x, y)
公式四
(公式一)
(公式二)
(公式三)
(公式四)
三角函数的诱导公式一---四
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系.
归纳:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
简记作:“函数名不变,符号看象限”
题型一 给角求值问题
[解] (1)sin(-1200°)
=-sin1200°
=-sin(3×360°+120°)
=-sin120
=-sin(180°-60°)
(2)tan945°=tan(2×360°+225°)
=tan225°
=tan(180°+45°)
=tan45°=1.
利用诱导公式解决给角求值问题的步骤
答案
解 (1)原式=sin(120°-4×360°)cos(30°+3×360°)+cos(60°-3×360°)sin(30°+2×360°)+tan(135°+360°)
=sin120°cos30°+cos60°sin30°+tan135°
题型二 给值求值问题
解决条件求值问题的策略
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
答案
解析 (1)∵cos(α+β)=-1,
∴α+β=π+2kπ,k∈Z,
∴sin(α+2β)=sin[(α+β)+β]
=sin(π+β)
题型三 三角函数式的化简
三角函数式化简的常用方法
(1)依据所给式子合理选用诱导公式将所给角的三角函数转化为另一个角的三角函数
.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
(3)注意“1”的应用:1=sin2α+cos2α=tan.
(4)用诱导公式进行化简时,若遇到kπ±α的形式,需对k进行分类讨论,然后再运用诱导公式进行化简.
课堂小结:通过这节课我学会了什么?还有哪些疑惑?
1.三角函数的四组诱导公式;
2.三角函数诱导公式的应用(求值、化简);
3.三角函数诱导公式的记忆方法。( ? )
一、基本内容:
二、思想方法:
1.数形结合
2.转化与化归
利用诱导公式一~四,可以求任意角的三角函数,其基本思路(步骤)是:
这是一种化归与转化的数学思想.
任意负角的
三角函数
任意正角的
三角函数
0~2π的角
的三角函数
锐角的三角
函数
用公式三或一
用公式一
用公式
二或四
负化正,大化小,化到锐角就终了
未知
已知
作业:
练习:1,2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
