5.6.2函数y=Asin(ωx φ)的图象 课件(共20张PPT)
文档属性
| 名称 | 5.6.2函数y=Asin(ωx φ)的图象 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 629.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 08:10:38 | ||
图片预览








文档简介
(共20张PPT)
函数Y=ASin(ωX+ψ)的图象
1. 函数Y=ASinX与Y=SinX
的图象的联系
例1
画出函数 Y=2 SinX,X∈R
Y=0.5 SinX,X∈R 的简图。
2π
0
-1/2
0
1/2
0
0.5Sin X
0
-2
0
2
0
2Sin X
0
-1
0
1
0
Sin X
3π/2
π
π/2
0
x
Y
O
X
-1
1
2
-2
0.5
-0.5
这两个函数的
周期都是2π ,
我们先画出它们
在[0, 2π]上的简图。
思考:
函数Y=2 SinX,X∈R
Y=0.5 SinX,X∈R
的值域是什么?
一般地,函数Y=ASinX,X∈R (其中A>0,
且A≠1)的图象,可以看作正弦曲线上所有点的纵坐标
伸长(当A>1时)或缩短(当0不变)而得到。这种变换叫做振幅变换,A叫做函数
Y=ASinX的振幅。
函数Y=ASinX,X∈R的值域是[-A,A],最大值是A,
最小值是-A。
Y=SinX
横坐标不变
纵坐标变为原来的A倍
Y=ASinX
2. 函数Y=SinωX与Y=SinX
的图象的联系
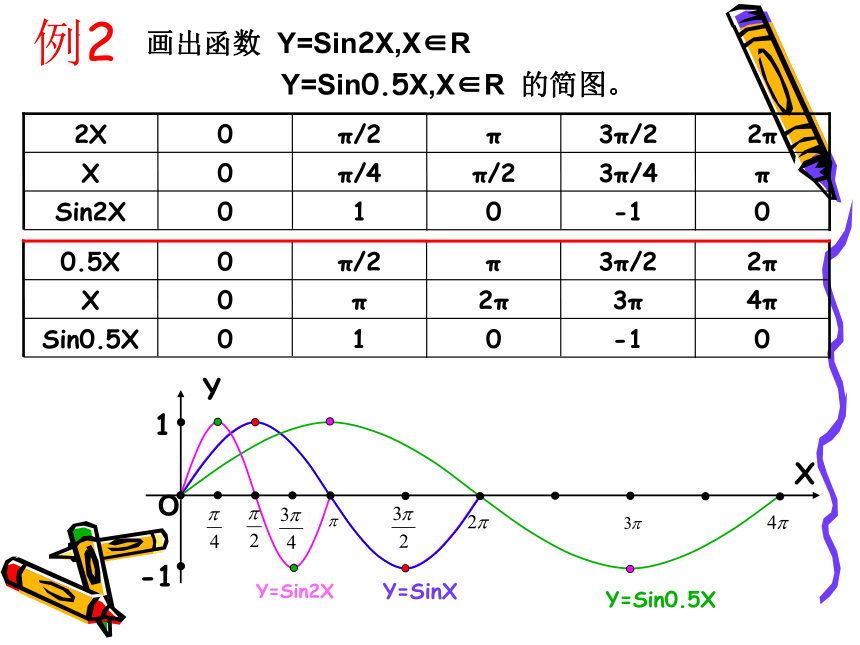
例2
画出函数 Y=Sin2X,X∈R
Y=Sin0.5X,X∈R 的简图。
0
-1
0
1
0
π
3π/4
π/2
π/4
0
2π
3π/2
π
π/2
0
Sin2X
X
2X
Y
O
X
-1
1
0
-1
0
1
0
4π
3π
2π
π
0
2π
3π/2
π
π/2
0
Sin0.5X
X
0.5X
Y=SinX
Y=Sin2X
Y=Sin0.5X
一般地,函数Y=SinωX,X∈R (其中ω>0,
且ω≠1)的图象,可以看作正弦曲线上所有点的横坐标
缩短(当ω>1时)或伸长(当0<ω<1时) 到原来的1/ω倍(纵坐标
不变)而得到。
这种变换称为周期变换。
Y=SinX
纵坐标不变
横坐标变为原来的1/ω倍
Y=SinωX
3. 函数Y=Sin(X+ψ)与Y=SinX的图象的联系
例3
画出函数 Y=Sin (X+ ),X∈R
Y=Sin(X- ) ,X∈R 的简图。
0
0
-1
0
1
-π/3
5π/3
7π/6
2π/3
π/6
0
2π
3π/2
π
π/2
Sin(X+ )
X
x +
0
0
-1
0
1
π/4
9π/4
7π/4
5π/4
3π/4
0
2π
3π/2
π
π/2
Sin(X- )
X
x-
Y
O
X
-1
1
一般地,函数Y=Sin(X+ψ),X∈R (其中ψ≠0)的
图象,可以看作正弦曲线上所有点向左(当ψ>0时)或向右
(当ψ<0时) 平行移动│ψ│个单位长度而得到。
这种变换称为平移变换。
Y=SinX
左移(ψ>0)或
右移(ψ<0) │ψ│
Y=Sin(X+ψ),
试一试
用五点法作出函数 在一个周期的闭区间上的简图。
练习
1. 画出函数Y=Sin(2X+ ),X∈R在长度为一个
周期的闭区间上的简图。
4
p
X
Y
O
-1
1
纵坐标不变
横坐标变为原来的1/ω倍
横坐标不变
纵坐标变为原来的A倍
小结:
1.用五点法作Y=ASin(ωX+ψ)函数的简图时,
首先把ωX+ψ看作一个整体Z,
再令Z=0, π/2,π,3π/2,2π,求出X,
最后,列表、描点、连线。
Y=SinX
Y=ASinX
3. 周期变换:
Y=SinX
Y=SinωX
4. 平移变换:
Y=SinX
Y=Sin(X+ψ),
左移(ψ>0)或
右移(ψ<0) │ψ│
2. 振幅变换:
按照下列指定的顺序,如何将一个函数的图象变为下一个函数的图象.
①
③
②
①
②
③
“先平移后伸缩”
函数 y=Asin(ωx+φ)的图象
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
方法1:
y=sin(x+ )
y=sinx
思考:若”先伸缩后平移”,具体过程又如何
①
③
②
②
①
③
“先伸缩后平移”
函数 y=Asin(ωx+φ)的图象
关键环节:
平移几个单位?
x
2x
x
(1)“数”
(2)“形”
π
o
y
x
(3)“式”
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=sinx
y=sin2x
y=3sin(2x+ )
方法2:
y=sinx
y=sin x
横坐标缩短( >1)或伸长(0< <1)到原来的1/ 倍
纵坐标伸长(A>1)或缩短(0y=Asin( x+ )
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
“先伸缩后平移”
向左( >0)或向右( <0)
函数 y=Asin(ωx+φ)的图象
y=sin( x+ )
一类图象:
两种作法:
三个参数:
①五点作图法
②变换作图法
伸缩变换
课堂小结
注意:先平移后伸缩、先伸缩后平移的变换区别
函数Y=ASin(ωX+ψ)的图象
1. 函数Y=ASinX与Y=SinX
的图象的联系
例1
画出函数 Y=2 SinX,X∈R
Y=0.5 SinX,X∈R 的简图。
2π
0
-1/2
0
1/2
0
0.5Sin X
0
-2
0
2
0
2Sin X
0
-1
0
1
0
Sin X
3π/2
π
π/2
0
x
Y
O
X
-1
1
2
-2
0.5
-0.5
这两个函数的
周期都是2π ,
我们先画出它们
在[0, 2π]上的简图。
思考:
函数Y=2 SinX,X∈R
Y=0.5 SinX,X∈R
的值域是什么?
一般地,函数Y=ASinX,X∈R (其中A>0,
且A≠1)的图象,可以看作正弦曲线上所有点的纵坐标
伸长(当A>1时)或缩短(当0
Y=ASinX的振幅。
函数Y=ASinX,X∈R的值域是[-A,A],最大值是A,
最小值是-A。
Y=SinX
横坐标不变
纵坐标变为原来的A倍
Y=ASinX
2. 函数Y=SinωX与Y=SinX
的图象的联系
例2
画出函数 Y=Sin2X,X∈R
Y=Sin0.5X,X∈R 的简图。
0
-1
0
1
0
π
3π/4
π/2
π/4
0
2π
3π/2
π
π/2
0
Sin2X
X
2X
Y
O
X
-1
1
0
-1
0
1
0
4π
3π
2π
π
0
2π
3π/2
π
π/2
0
Sin0.5X
X
0.5X
Y=SinX
Y=Sin2X
Y=Sin0.5X
一般地,函数Y=SinωX,X∈R (其中ω>0,
且ω≠1)的图象,可以看作正弦曲线上所有点的横坐标
缩短(当ω>1时)或伸长(当0<ω<1时) 到原来的1/ω倍(纵坐标
不变)而得到。
这种变换称为周期变换。
Y=SinX
纵坐标不变
横坐标变为原来的1/ω倍
Y=SinωX
3. 函数Y=Sin(X+ψ)与Y=SinX的图象的联系
例3
画出函数 Y=Sin (X+ ),X∈R
Y=Sin(X- ) ,X∈R 的简图。
0
0
-1
0
1
-π/3
5π/3
7π/6
2π/3
π/6
0
2π
3π/2
π
π/2
Sin(X+ )
X
x +
0
0
-1
0
1
π/4
9π/4
7π/4
5π/4
3π/4
0
2π
3π/2
π
π/2
Sin(X- )
X
x-
Y
O
X
-1
1
一般地,函数Y=Sin(X+ψ),X∈R (其中ψ≠0)的
图象,可以看作正弦曲线上所有点向左(当ψ>0时)或向右
(当ψ<0时) 平行移动│ψ│个单位长度而得到。
这种变换称为平移变换。
Y=SinX
左移(ψ>0)或
右移(ψ<0) │ψ│
Y=Sin(X+ψ),
试一试
用五点法作出函数 在一个周期的闭区间上的简图。
练习
1. 画出函数Y=Sin(2X+ ),X∈R在长度为一个
周期的闭区间上的简图。
4
p
X
Y
O
-1
1
纵坐标不变
横坐标变为原来的1/ω倍
横坐标不变
纵坐标变为原来的A倍
小结:
1.用五点法作Y=ASin(ωX+ψ)函数的简图时,
首先把ωX+ψ看作一个整体Z,
再令Z=0, π/2,π,3π/2,2π,求出X,
最后,列表、描点、连线。
Y=SinX
Y=ASinX
3. 周期变换:
Y=SinX
Y=SinωX
4. 平移变换:
Y=SinX
Y=Sin(X+ψ),
左移(ψ>0)或
右移(ψ<0) │ψ│
2. 振幅变换:
按照下列指定的顺序,如何将一个函数的图象变为下一个函数的图象.
①
③
②
①
②
③
“先平移后伸缩”
函数 y=Asin(ωx+φ)的图象
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
方法1:
y=sin(x+ )
y=sinx
思考:若”先伸缩后平移”,具体过程又如何
①
③
②
②
①
③
“先伸缩后平移”
函数 y=Asin(ωx+φ)的图象
关键环节:
平移几个单位?
x
2x
x
(1)“数”
(2)“形”
π
o
y
x
(3)“式”
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=sinx
y=sin2x
y=3sin(2x+ )
方法2:
y=sinx
y=sin x
横坐标缩短( >1)或伸长(0< <1)到原来的1/ 倍
纵坐标伸长(A>1)或缩短(0
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
“先伸缩后平移”
向左( >0)或向右( <0)
函数 y=Asin(ωx+φ)的图象
y=sin( x+ )
一类图象:
两种作法:
三个参数:
①五点作图法
②变换作图法
伸缩变换
课堂小结
注意:先平移后伸缩、先伸缩后平移的变换区别
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
