人教版九年级上册数学22.2二次函数与一元二次方程导学练(附答案)
文档属性
| 名称 | 人教版九年级上册数学22.2二次函数与一元二次方程导学练(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 90.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 13:19:53 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级上册数学二次函数与一元二次方程导学练(附答案)
一、单选题
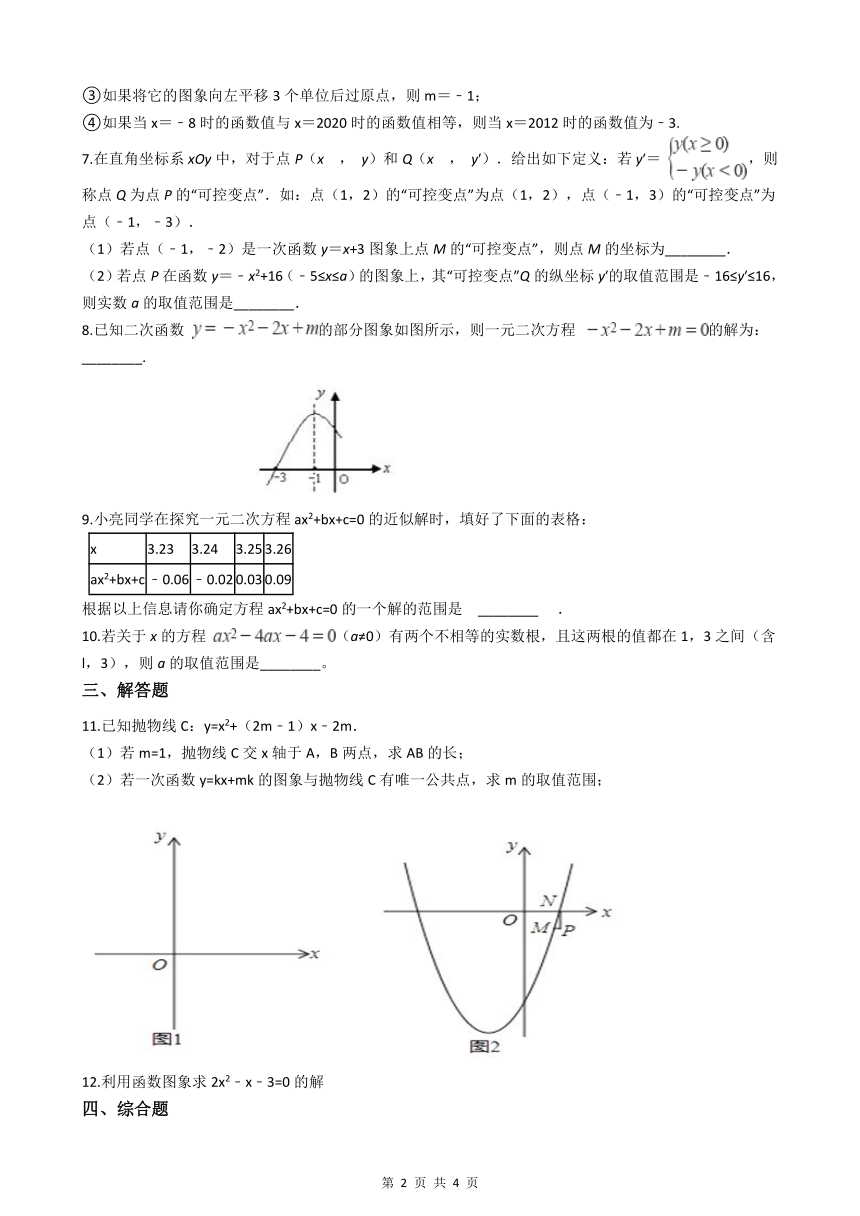
1.二次函数y=ax2+bx(a , b为常数)的图象如图所示,设关于x的一元二次方程ax2+bx+m=1的两个实数根分别为x1 , x2 , 若x1 x2>0,则实数m的取值范围是( )
A. 0≤m<3 B. 0<m≤3 C. 1≤m<4 D. 1<m≤4
2.已知函数y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c﹣4=0的根的情况是
A. 有两个相等的实数根 B. 有两个异号的实数根 C. 有两个不相等的实数根 D. 没有实数根
3.把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数 的图象与x轴有两个不同交点的概率是( ).
A. B. C. D.
4.在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac。设函数y1 , y2 , y3的图象与x轴的交点个数分别为M1 , M2 , M3 , ( )
A. 若M1=2,M2=2,则M3=0 B. 若M1=1,M2=0,则M3=0
C. 若M1=0,M2=2,则M3=0 D. 若M1=0,M2=0,则M3=0
5.如图,抛物线y=ax2+bx+c(a≠0)经过点(-1,0),对称轴为:直线x=1,则下列结论中正确的是( )
A. a>0 B. 当x>1时,y随x的增大而增大
C. c<0 D. x=3是一元二次方程ax2+bx+c=0(a≠0)的一个根
二、填空题
6.对于二次函数y=x2﹣2mx﹣3,下列正确的说法是________.
①它的图象与x轴有两个公共点;②如果当x≤1时,y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=﹣1;
④如果当x=﹣8时的函数值与x=2020时的函数值相等,则当x=2012时的函数值为﹣3.
7.在直角坐标系xOy中,对于点P(x , y)和Q(x , y′).给出如下定义:若y′= ,则称点Q为点P的“可控变点”.如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为________.
(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的取值范围是________.
8.已知二次函数 的部分图象如图所示,则一元二次方程 的解为:________.
9.小亮同学在探究一元二次方程ax2+bx+c=0的近似解时,填好了下面的表格:
x 3.23 3.24 3.25 3.26
ax2+bx+c ﹣0.06 ﹣0.02 0.03 0.09
根据以上信息请你确定方程ax2+bx+c=0的一个解的范围是 ________ .
10.若关于x的方程 (a≠0)有两个不相等的实数根,且这两根的值都在1,3之间(含l,3),则a的取值范围是________。
三、解答题
11.已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
12.利用函数图象求2x2﹣x﹣3=0的解
四、综合题
13.已知抛物线y=x2-(m+1)x+m,
(1)求证:抛物线与x轴一定有交点;
(2)若抛物线与x轴交于A(x1,0),B(x2,0)两点,x1﹤0﹤x2,且 ,求m的值.
14.某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
答 案
一、单选题
1. D 2. A 3. C 4. B 5. D
二、填空题
6. ①④ 7. (1)(﹣1,2)(2)a=4
8. 9. 3.24<x<3.25 10.
三、解答题
11. 解:(1)m=1时,抛物线为:y=x2+x﹣2,
令y=0得到:x2+x﹣2=0,解得x=﹣2或1,
所以点A(﹣2,0),点B(1,0),
所以AB=3.
(2)由消去y得到:x2+(2m﹣1﹣k)x﹣2m﹣mk=0,
∵一次函数y=kx+mk的图象与抛物线有唯一公共点,∴△=0,∴(2m﹣1﹣k)2+8m+4mk=0,
整理得:﹣4m2﹣4m=(k+1)2 ,
∵(k+1)2≥0,
设y=﹣4m2﹣4m,当y≥0时,﹣1≤m≤0,
∴﹣1≤m≤0时,一次函数y=kx+mk的图象与抛物线C有唯一公共点.
12. 解:列表如下:
x … ﹣2 ﹣1 0 1 2 …
Y=2x2﹣x﹣3 … 7 0 ﹣3 ﹣2 3 …
描点,连线,画出函数y=2x2﹣x﹣3的图象,如答图所示,
由图象得出抛物线与x轴两交点坐标A, B(﹣1,0),
故方程2x2﹣x﹣3=0的解为x1=, x2=﹣1.
四、综合题
13. (1)证明:∵ =[-(m+1)]2-4m=(m-1)2 , 无论m为何值,都有(m-1)2≥0,即 ≥0,
∴抛物线与x轴一定有交点
(2)解:OA=-x1 , OB=x2 ,
由 得 ,变形得 ,
∵ =m+1, =m,∴ ,解得,m=-4,
经检验,m=-4是方程的根
14. (1)解:设函数的表达式为y=kx+b,该一次函数过点(12,74),(28,66),
得 ,解得 ,
∴该函数的表达式为y=﹣0.5x+80,
(2)解:根据题意,得,(﹣0.5x+80)(80+x)=6750,解得,x1=10,x2=70
∵投入成本最低.∴x2=70不满足题意,舍去.
∴增种果树10棵时,果园可以收获果实6750千克.
(3)解:根据题意,得
w=(﹣0.5x+80)(80+x) =﹣0.5 x2+40 x+6400=﹣0.5(x﹣40)2+7200
∵a=﹣0.5<0,则抛物线开口向下,函数有最大值
∴当x=40时,w最大值为7200千克.
∴当增种果树40棵时果园的最大产量是7200千克.
(
第
- 1 -
页 共
6
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级上册数学二次函数与一元二次方程导学练(附答案)
一、单选题
1.二次函数y=ax2+bx(a , b为常数)的图象如图所示,设关于x的一元二次方程ax2+bx+m=1的两个实数根分别为x1 , x2 , 若x1 x2>0,则实数m的取值范围是( )
A. 0≤m<3 B. 0<m≤3 C. 1≤m<4 D. 1<m≤4
2.已知函数y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c﹣4=0的根的情况是
A. 有两个相等的实数根 B. 有两个异号的实数根 C. 有两个不相等的实数根 D. 没有实数根
3.把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数 的图象与x轴有两个不同交点的概率是( ).
A. B. C. D.
4.在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac。设函数y1 , y2 , y3的图象与x轴的交点个数分别为M1 , M2 , M3 , ( )
A. 若M1=2,M2=2,则M3=0 B. 若M1=1,M2=0,则M3=0
C. 若M1=0,M2=2,则M3=0 D. 若M1=0,M2=0,则M3=0
5.如图,抛物线y=ax2+bx+c(a≠0)经过点(-1,0),对称轴为:直线x=1,则下列结论中正确的是( )
A. a>0 B. 当x>1时,y随x的增大而增大
C. c<0 D. x=3是一元二次方程ax2+bx+c=0(a≠0)的一个根
二、填空题
6.对于二次函数y=x2﹣2mx﹣3,下列正确的说法是________.
①它的图象与x轴有两个公共点;②如果当x≤1时,y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=﹣1;
④如果当x=﹣8时的函数值与x=2020时的函数值相等,则当x=2012时的函数值为﹣3.
7.在直角坐标系xOy中,对于点P(x , y)和Q(x , y′).给出如下定义:若y′= ,则称点Q为点P的“可控变点”.如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为________.
(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的取值范围是________.
8.已知二次函数 的部分图象如图所示,则一元二次方程 的解为:________.
9.小亮同学在探究一元二次方程ax2+bx+c=0的近似解时,填好了下面的表格:
x 3.23 3.24 3.25 3.26
ax2+bx+c ﹣0.06 ﹣0.02 0.03 0.09
根据以上信息请你确定方程ax2+bx+c=0的一个解的范围是 ________ .
10.若关于x的方程 (a≠0)有两个不相等的实数根,且这两根的值都在1,3之间(含l,3),则a的取值范围是________。
三、解答题
11.已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
12.利用函数图象求2x2﹣x﹣3=0的解
四、综合题
13.已知抛物线y=x2-(m+1)x+m,
(1)求证:抛物线与x轴一定有交点;
(2)若抛物线与x轴交于A(x1,0),B(x2,0)两点,x1﹤0﹤x2,且 ,求m的值.
14.某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
答 案
一、单选题
1. D 2. A 3. C 4. B 5. D
二、填空题
6. ①④ 7. (1)(﹣1,2)(2)a=4
8. 9. 3.24<x<3.25 10.
三、解答题
11. 解:(1)m=1时,抛物线为:y=x2+x﹣2,
令y=0得到:x2+x﹣2=0,解得x=﹣2或1,
所以点A(﹣2,0),点B(1,0),
所以AB=3.
(2)由消去y得到:x2+(2m﹣1﹣k)x﹣2m﹣mk=0,
∵一次函数y=kx+mk的图象与抛物线有唯一公共点,∴△=0,∴(2m﹣1﹣k)2+8m+4mk=0,
整理得:﹣4m2﹣4m=(k+1)2 ,
∵(k+1)2≥0,
设y=﹣4m2﹣4m,当y≥0时,﹣1≤m≤0,
∴﹣1≤m≤0时,一次函数y=kx+mk的图象与抛物线C有唯一公共点.
12. 解:列表如下:
x … ﹣2 ﹣1 0 1 2 …
Y=2x2﹣x﹣3 … 7 0 ﹣3 ﹣2 3 …
描点,连线,画出函数y=2x2﹣x﹣3的图象,如答图所示,
由图象得出抛物线与x轴两交点坐标A, B(﹣1,0),
故方程2x2﹣x﹣3=0的解为x1=, x2=﹣1.
四、综合题
13. (1)证明:∵ =[-(m+1)]2-4m=(m-1)2 , 无论m为何值,都有(m-1)2≥0,即 ≥0,
∴抛物线与x轴一定有交点
(2)解:OA=-x1 , OB=x2 ,
由 得 ,变形得 ,
∵ =m+1, =m,∴ ,解得,m=-4,
经检验,m=-4是方程的根
14. (1)解:设函数的表达式为y=kx+b,该一次函数过点(12,74),(28,66),
得 ,解得 ,
∴该函数的表达式为y=﹣0.5x+80,
(2)解:根据题意,得,(﹣0.5x+80)(80+x)=6750,解得,x1=10,x2=70
∵投入成本最低.∴x2=70不满足题意,舍去.
∴增种果树10棵时,果园可以收获果实6750千克.
(3)解:根据题意,得
w=(﹣0.5x+80)(80+x) =﹣0.5 x2+40 x+6400=﹣0.5(x﹣40)2+7200
∵a=﹣0.5<0,则抛物线开口向下,函数有最大值
∴当x=40时,w最大值为7200千克.
∴当增种果树40棵时果园的最大产量是7200千克.
(
第
- 1 -
页 共
6
页
)
同课章节目录
