直线与圆的位置关系复习课[下学期]

课件10张PPT。直线与圆的位置关系复习课初三数学组教学目标：知识目标：
1.了解直线与圆的位置关系,能用数量关系判断直线与圆的位置关系;
2.掌握切线的判定与切线的性质;
3.理解弦切角的概念,能够运用弦切角定理及推论进行角的计算;
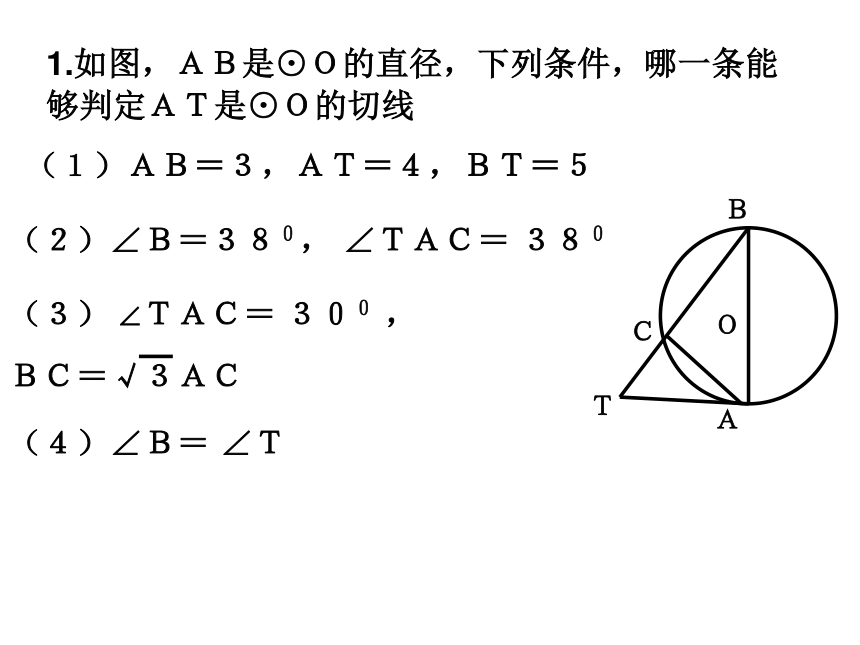
4.理解并掌握圆幂定理的内容及图形的变化,并能运用定理进行圆中比例线段的证明或计算.能力目标：通过复习培养学生综合运用知识的能力.情感目标：体会曲线型图形圆与三角形、四边形间的联系.教学重点：切线的判定和性质的运用及圆中比例线段.教学难点：圆中的比例线段.1．直线与圆的位置关系：设⊙O的半径为r，圆心到直线的距离为d，则（1）直线与⊙O相切，等价于d＝r；（2）直线与⊙O相交，等价于dr．2．圆的切线的判定：（1）直线与圆只有一个交点；（2）圆心到直线的距离等于半径；（3）直线过半径的外端，并且垂直于这条半径． 3．圆的切线的性质：（1）圆的切线垂直于过切点的半径；（2）经过圆心且垂直于切线的直线必过切点；（3）经过切点且垂直于切线的直线必过圆心．二、直线与圆4．切线长定理：从圆外一点引圆的两条切线，它们的长相等，这点于圆心的连线平分两条切线的夹角．5.弦切角:6.圆幂定理:1.如图，ＡＢ是⊙Ｏ的直径，下列条件，哪一条能够判定ＡＴ是⊙Ｏ的切线（１）ＡＢ＝３，ＡＴ＝４，ＢＴ＝５（２）∠Ｂ＝３８０， ∠ＴＡＣ＝ ３８０ （３） ∠ＴＡＣ＝ ３００ ，
ＢＣ＝√３ＡＣＢ（４）∠Ｂ＝ ∠Ｔ ２．已知：直线Ｌ的解析式为y= x+m(m为常
数，m≠0）,点Ｂ（－４，３）在直线Ｌ上．
（１）求m的值；
（２）若⊙Ａ的圆心为原点，半径为Ｒ，并且⊙Ａ与直线Ｌ有公共点，度求Ｒ的取值范围．３．如图，ＡB是⊙Ｏ的直径，⊙Ｏ过ＡＣ的中点Ｄ，ＤＥ⊥ＢＣ，垂足为Ｅ．
（１）由这些条件，写出四个正确的结论（不添辅助线）．
（２）若∠ＡＢＣ为直角，其它条件不变，除上述结论外，再写两个结论，并画出图形．（也不添辅助线）．４．如图，已知?ＡＢＣ内接于⊙Ｏ，ＡＥ切⊙Ｏ于点Ａ，ＢＣ∥ＡＥ．
（１）求证：?ＡＢＣ是等腰三角形．
（２）设ＡＢ＝１０，ＢＣ＝８，点Ｐ是射线ＡＥ上一点，若以Ａ、Ｐ、Ｃ为顶点的三角形与?ＡＢＣ相似，问这样的顶点有几个．并求ＡＰ的长．５．如图，ＰＮ切⊙Ｏ于Ｎ点，过点Ｐ和ＰＮ的中点Ｍ作⊙Ｏ１，交⊙Ｏ于Ａ，Ｂ两点，ＢＡ的延长线交ＰＮ于Ｑ点，求ＭＱ：ＱＮ：ＰＭ的值．如图,在⊙O中,弦AB和直径CD相交于P,M是DC延长线的一点,MN是⊙O的切线,N为切点.已知AP=8,PB=6,PD=4,MC=6,求MN.课堂练习