广东省培正中学2013年高一数学必修二立体几何测试题(2013-11-26)
文档属性
| 名称 | 广东省培正中学2013年高一数学必修二立体几何测试题(2013-11-26) |

|
|
| 格式 | zip | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-23 15:55:36 | ||
图片预览


文档简介
广东省培正中学2013年高一数学必修二立体几何测试题 2013-11-26
一 :选择题(4分题)
1.下面四个条件中,能确定一个平面的条件是( )
A. 空间任意三点 B.空间两条直线 C.空间两条平行直线 D.一条直线和一个点
2.,,是空间三条不同的直线,则下列命题正确的是( ).
A., B.,
C.,,共面 D.,,共点,,共面
3.已知m,n是两条不同的直线,是三个不同的平面,下列命题中正确的是:
A.若,则∥ B.若,则∥
C.若∥,∥,则∥ D.若∥,∥,则∥
4.在四面体的四个面中,是直角三角形的面至多有( )
A.0 个 B.1个 C. 3个 D .4个
5,下列命题中错误的是
A.如果平面,那么平面内一定存在直线平行于平面
B.如果平面α不垂直于平面,那么平面内一定不存在直线垂直于平面
C.如果平面,平面,,那么
D.如果平面,那么平面内所有直线都垂直于平面
6.如图所示正方体,下面结论错误的是( )
A.
B.
C.
D. 异面直线角为
7.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角是( )
A. B. C. D.
8.把正方形沿对角线折成直二面角后,下列命题正确的是( )
A. B. C. D.
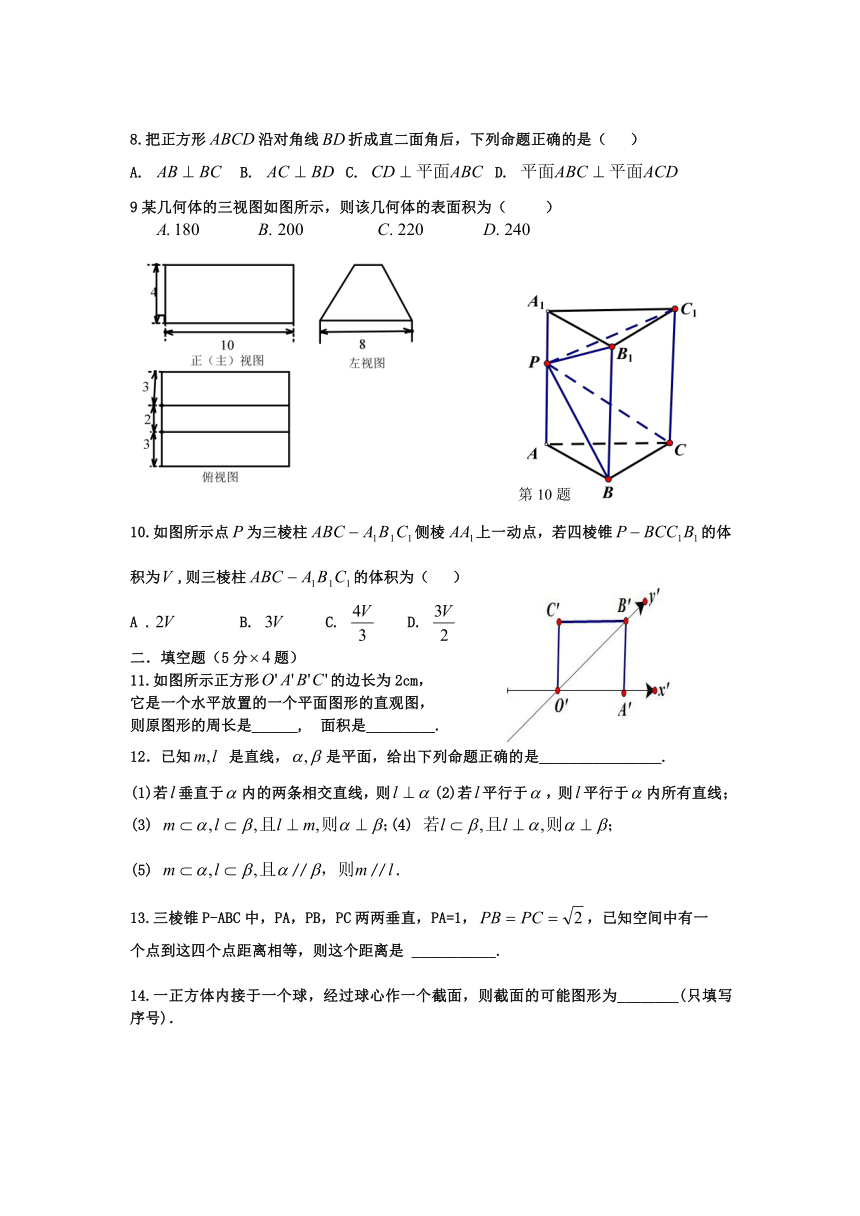
9某几何体的三视图如图所示,则该几何体的表面积为( )
10.如图所示点为三棱柱侧棱上一动点,若四棱锥的体积为,则三棱柱的体积为( )
A . B. C. D.
二.填空题(5分题)
11.如图所示正方形的边长为2cm,
它是一个水平放置的一个平面图形的直观图,
则原图形的周长是______, 面积是_________.
12.已知 是直线,是平面,给出下列命题正确的是________________.
(1)若垂直于内的两条相交直线,则(2)若平行于,则平行于内所有直线;
(3) (4)
(5) ////.
13.三棱锥P-ABC中,PA,PB,PC两两垂直,PA=1,,已知空间中有一
个点到这四个点距离相等,则这个距离是 ___________.
14.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为________(只填写序号).
二.填空题:
11.__________ ____________ 12.______________________
13.________________________ 14._______________________
三.解答题
15.已知圆台的上下底面半径分别为2,6,且侧面面积等于两底面面积之和,求该圆台的母线长,侧面积及体积.
16. 已知四棱锥的三视图如下:
1)画出四棱锥的直观图
2)求四棱锥的体积;
3求四棱锥的表面积;
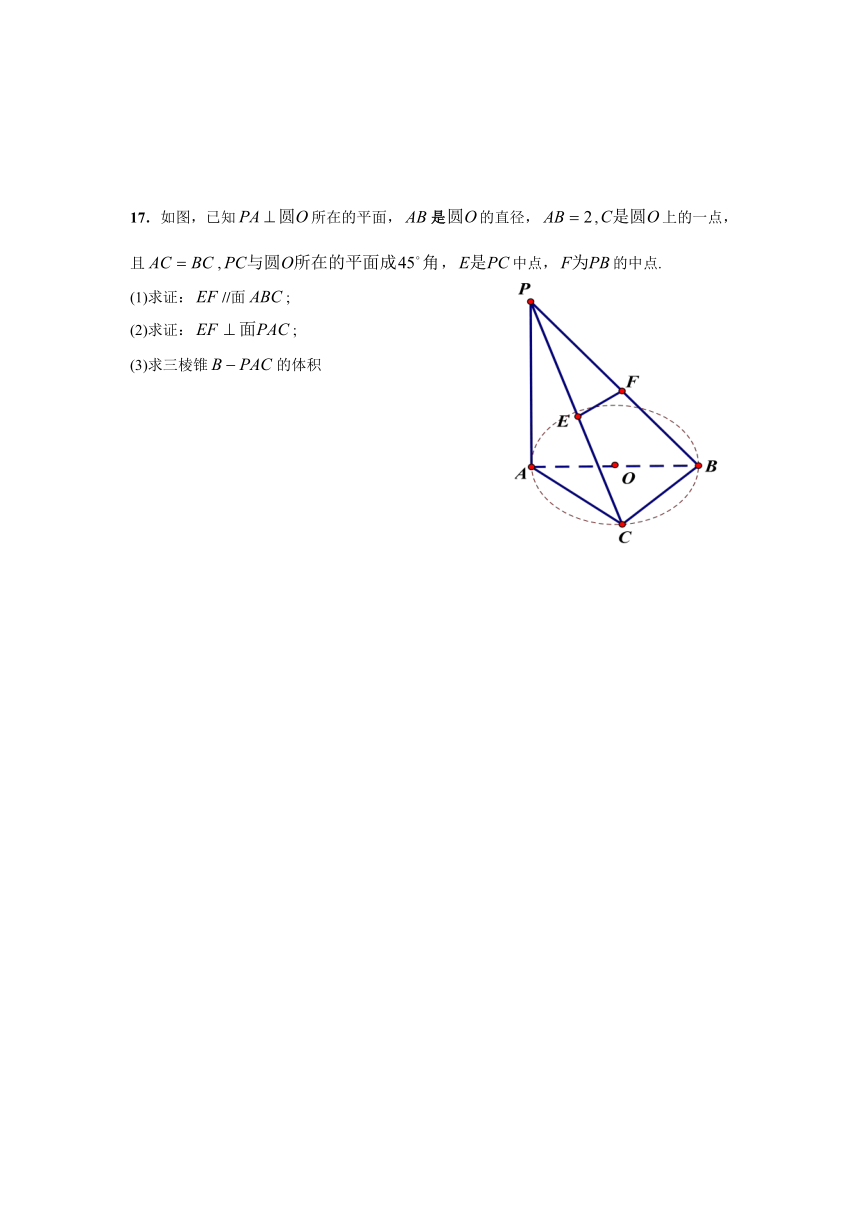
17.如图,已知所在的平面,是的直径,,上的一点,且,,中点,的中点.
(1)求证://面;
(2)求证:;
(3)求三棱锥的体积
18,如图,在三棱锥中,平面平面,,,过 作,垂足为,点分别是棱的中点.
求证:(1)平面平面;
(2).
19. 如图1,在中,,分别为的中点,点为线段上的一点,将沿折起到的位置,使,如图2。
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)线段上是否存在点,使平面?说明理由。
高一立体几何测试答案
一:1-5;CBBDD 6-10;DCBDD
二:11._16cm_; 8____12._1,4____13. ; 14. ①②③
15.母线长为5,侧面积为40,高为3,体积为52.
16.(1)
(2)由直观图可知此空间几何体为四棱锥,由正视图可知高为2,
所以
(3)由题意可知
由勾股定理逆定理可知
所以
18.证:(1),,,由题,,平面平面,平面,同理平面,与为平面内的两条相交直线,∴平面平面,
(2)平面平面于,平面,平面,,
又且与为平面内的两条相交直线,。
19.(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE平面A1CB,所以DE∥平面A1CB.
(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A1F 平面A1DC,
所以DE⊥A1F.又因为A1F⊥CD,所以A1F⊥平面BCDE.所以A1F⊥BE
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,
分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP.
由(2)知DE⊥平面A1DC,所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C 的中点,
所以A1C⊥DP,所以A1C⊥平面DEP,从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.
一 :选择题(4分题)
1.下面四个条件中,能确定一个平面的条件是( )
A. 空间任意三点 B.空间两条直线 C.空间两条平行直线 D.一条直线和一个点
2.,,是空间三条不同的直线,则下列命题正确的是( ).
A., B.,
C.,,共面 D.,,共点,,共面
3.已知m,n是两条不同的直线,是三个不同的平面,下列命题中正确的是:
A.若,则∥ B.若,则∥
C.若∥,∥,则∥ D.若∥,∥,则∥
4.在四面体的四个面中,是直角三角形的面至多有( )
A.0 个 B.1个 C. 3个 D .4个
5,下列命题中错误的是
A.如果平面,那么平面内一定存在直线平行于平面
B.如果平面α不垂直于平面,那么平面内一定不存在直线垂直于平面
C.如果平面,平面,,那么
D.如果平面,那么平面内所有直线都垂直于平面
6.如图所示正方体,下面结论错误的是( )
A.
B.
C.
D. 异面直线角为
7.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角是( )
A. B. C. D.
8.把正方形沿对角线折成直二面角后,下列命题正确的是( )
A. B. C. D.
9某几何体的三视图如图所示,则该几何体的表面积为( )
10.如图所示点为三棱柱侧棱上一动点,若四棱锥的体积为,则三棱柱的体积为( )
A . B. C. D.
二.填空题(5分题)
11.如图所示正方形的边长为2cm,
它是一个水平放置的一个平面图形的直观图,
则原图形的周长是______, 面积是_________.
12.已知 是直线,是平面,给出下列命题正确的是________________.
(1)若垂直于内的两条相交直线,则(2)若平行于,则平行于内所有直线;
(3) (4)
(5) ////.
13.三棱锥P-ABC中,PA,PB,PC两两垂直,PA=1,,已知空间中有一
个点到这四个点距离相等,则这个距离是 ___________.
14.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为________(只填写序号).
二.填空题:
11.__________ ____________ 12.______________________
13.________________________ 14._______________________
三.解答题
15.已知圆台的上下底面半径分别为2,6,且侧面面积等于两底面面积之和,求该圆台的母线长,侧面积及体积.
16. 已知四棱锥的三视图如下:
1)画出四棱锥的直观图
2)求四棱锥的体积;
3求四棱锥的表面积;
17.如图,已知所在的平面,是的直径,,上的一点,且,,中点,的中点.
(1)求证://面;
(2)求证:;
(3)求三棱锥的体积
18,如图,在三棱锥中,平面平面,,,过 作,垂足为,点分别是棱的中点.
求证:(1)平面平面;
(2).
19. 如图1,在中,,分别为的中点,点为线段上的一点,将沿折起到的位置,使,如图2。
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)线段上是否存在点,使平面?说明理由。
高一立体几何测试答案
一:1-5;CBBDD 6-10;DCBDD
二:11._16cm_; 8____12._1,4____13. ; 14. ①②③
15.母线长为5,侧面积为40,高为3,体积为52.
16.(1)
(2)由直观图可知此空间几何体为四棱锥,由正视图可知高为2,
所以
(3)由题意可知
由勾股定理逆定理可知
所以
18.证:(1),,,由题,,平面平面,平面,同理平面,与为平面内的两条相交直线,∴平面平面,
(2)平面平面于,平面,平面,,
又且与为平面内的两条相交直线,。
19.(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE平面A1CB,所以DE∥平面A1CB.
(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A1F 平面A1DC,
所以DE⊥A1F.又因为A1F⊥CD,所以A1F⊥平面BCDE.所以A1F⊥BE
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,
分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP.
由(2)知DE⊥平面A1DC,所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C 的中点,
所以A1C⊥DP,所以A1C⊥平面DEP,从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.
