人教A版(2019)高中数学必修第二册 9.2.1总体取值规律的估计+9.2.2总体百分位数的估计 课件(共45张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 9.2.1总体取值规律的估计+9.2.2总体百分位数的估计 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览








文档简介
(共45张PPT)
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
一
二
三
四
一、频数与频率
1.将一批数据按要求分为若干个组,各组内数据的个数叫做该组的频数.每组数据的频数除以全体数据的个数的商叫做该组数据的频率.频率反映各个小组数据在样本中所占比例的大小.
2.做一做
容量为100的样本数据被分为6组,如表:
第5组的频率是( )
A.0.15 B.0.16 C.0.18 D.0.20
答案:B
解析:由表可知,第5组的频数为100-14-17-18-20-15=16,∴第5组的频率为 =0.16.故选B.
一
二
三
四
二、频率分布表
1.思考
(1)我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 你认为为了较为合理地确定出这个标准需要做哪些工作
提示a定为大部分居民的月均用水量比较合理.为了制定一个较为合理的标准a,必须先了解全市居民日常用水量的分布情况,比如月均用水量在哪个范围的居民最多,他们占全市居民的百分比情况等.
一
二
三
四
(2)一般地,列出一组样本数据的频率分布表可以分哪几个步骤进行
提示第一步,求极差.
第二步,决定组距与组数.
第三步,确定分组点,将数据分组.
第四步,列频率分布表.
一
二
三
四
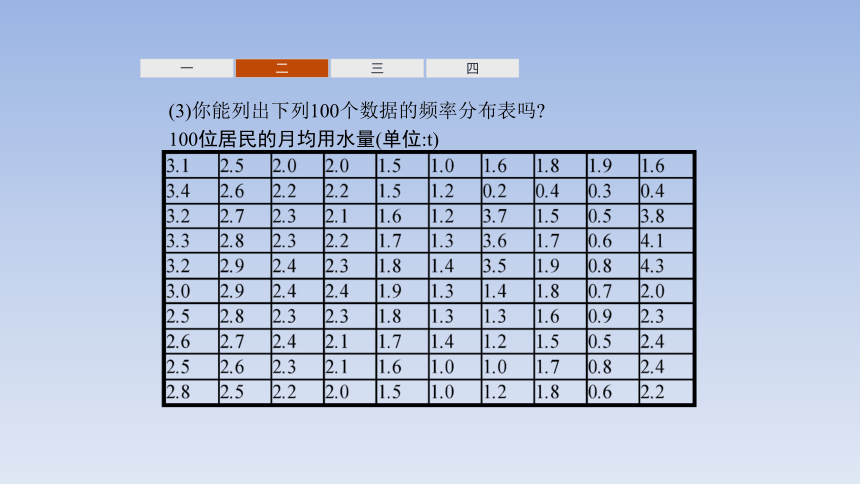
(3)你能列出下列100个数据的频率分布表吗
100位居民的月均用水量(单位:t)
一
二
三
四
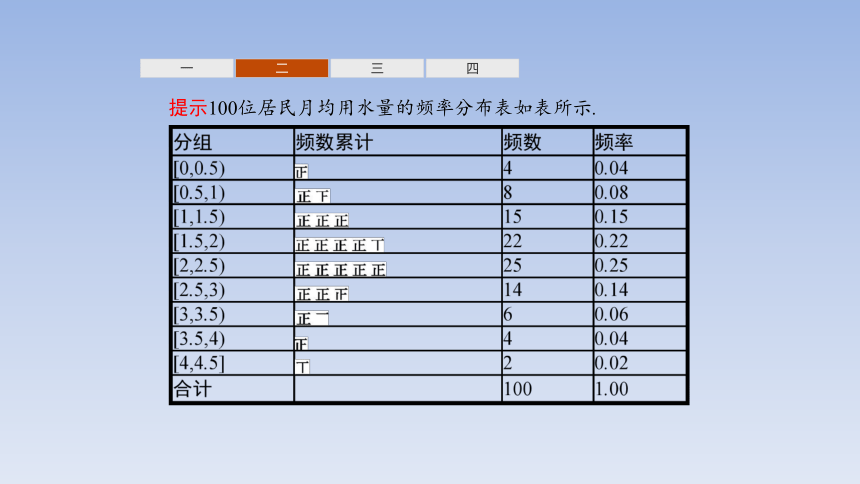
提示100位居民月均用水量的频率分布表如表所示.
一
二
三
四
2.填空
为了能直观地显示样本的频率分布情况,通常将样本量、样本中出现该事件的频数以及计算所得的相应频率列在一张表中,这张表叫做频率分布表.
一
二
三
四
三、频率分布直方图
1.思考
(1)为了将频率分布表中的结果直观形象地表现出来,常画出频率分布直方图.画图时,应以横轴表示分组、纵轴表示各组频率与组距的比值,以各个组距为底,以各频率除以组距的商为高,画成小长方形,这样得到的直方图就是频率分布直方图.
(2)为了直观反映样本数据在各组中的分布情况,你能根据上面的频率分布表画出频率分布直方图吗
提示频率分布直方图为:
一
二
三
四
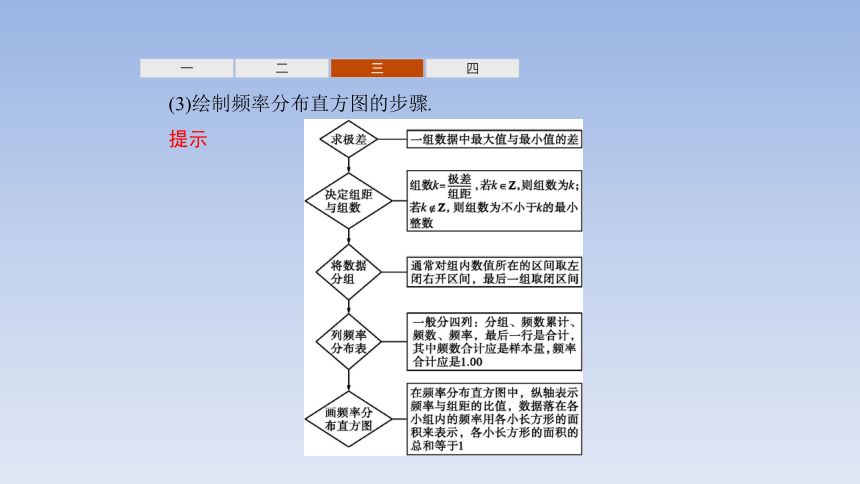
(3)绘制频率分布直方图的步骤.
提示
一
二
三
四
2.做一做
(1)在样本频率分布直方图中,某个小长方形的面积是其他小长方形的面积之和的14,已知样本量是80,则该组的频数为( )
A.20 B.16 C.30 D.35
答案:B
解析:设该组的频数为x,则其他组的频数之和为4x,由样本量是80,得x+4x=80,解得x=16,即该组的频数为16,故选B.
一
二
三
四
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①频率分布直方图中的纵轴表示频率.( )
②频率分布直方图中每个小长方形的面积等于相应组的频率.( )
③频率分布直方图中所有小长方形的面积和等于1.( )
答案:①× ②√ ③√
一
二
三
四
四、第p百分位数
1.思考
现有一组数据3.1,2.4,2.0,1.6,1.8.
则这组数据的中位数是多少 第50百分位数是多少 若数据变为3.1,2.4,2.0,1.6结论又如何 你能发现其中的规律吗
提示第一组数据的中位数为2.0,第50百分位数2.0;
第二组数据的中位数为2.2,第50百分位数为2.2.
从以上过程可以归纳出一组数据的中位数其实就是第50百分位数.
一
二
三
四
2.填空
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
一
二
三
四
3.做一做
(1)数据1,3,8,5的中位数是 ,第50百分位数是 ,第75百分位数是 .
答案:4 4 6.5
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①任何一组数据的第50百分位数与中位数的值是相同的.( )
②第25百分位数也可以称为第一四分位数或上四分位数.( )
答案:①√ ②×
探究一
探究二
探究三
探究四
思维辨析
随堂演练
频率分布直方图的绘制与应用
例1一个农技站为了考察某种麦穗长的分布情况,在一块试验地里抽取了100个麦穗,量得长度如下(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
探究一
探究二
探究三
探究四
思维辨析
随堂演练
根据上面的数据列出频率分布表、绘出频率分布直方图,并估计长度在[5.75,6.05)cm之间的麦穗在这批麦穗中所占的百分比.
分析依据步骤画出频率分布直方图;用样本中的百分比(即频率)来估计长度在[5.75,6.05)cm之间的麦穗在这批麦穗中所占的百分比.
解:步骤是:
(1)计算极差,7.4-4.0=3.4(cm).
(2)决定组距与组数.
若取组距为0.3 cm,由于 ,需分成12组,组数合适.于是取定组距为0.3 cm,组数为12.
(3)将数据分组.
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点.则所分的12个小组可以是[3.95,4.25),[4.25,4.55),[4.55,4.85),…,[7.25,7.55].
探究一
探究二
探究三
探究四
思维辨析
随堂演练
(4)列频率分布表.
对各个小组作频数累计,然后数频数,算频率,列频率分布表,如下表所示:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
探究一
探究二
探究三
探究四
思维辨析
随堂演练
(5)画频率分布直方图,如图.
从表中看到,样本数据落在[5.75,6.05)之间的频率是0.28,于是可以估计,在这块地里,长度在[5.75,6.05)cm之间的麦穗约占28%.
反思感悟 本题画频率分布直方图时,小长方形的高易错用该组的频率的大小来表示.其原因是不清楚频率分布直方图纵轴的意义.由于画频率分布直方图的步骤比较烦琐,因此在实际操作的过程中要有足够的耐心.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练1为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组情况与频数如下:
[10.75,10.85),3;[10.85,10.95),9;[10.95,11.05),13;[11.05,11.15),16;[11.15,11.25),26;[11.25,11.35),20;[11.35,11.45),7;[11.45,11.55),4;[11.55,11.65],2.
(1)列出频率分布表;
(2)画出频率分布直方图以及频率分布折线图;
(3)根据上述图表,估计数据落在[10.95,11.35)范围内的可能性是百分之几;
(4)估计数据小于11.20的可能性是百分之几.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)频率分布表如下:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
(2)频率分布直方图及频率分布折线图如图:
(3)由上述图表可知数据落在[10.95,11.35)范围内的频率为0.13+0.16+0.26+0.20=0.75=75%,即数据落在[10.95,11.35)范围内的可能性是75%.
(4)数据小于11.20的可能性即数据小于11.20的频率,设为x,则(x-0.41)÷(11.20-11.15)=(0.67-0.41)÷(11.25-11.15),所以x-0.41=0.13,即x=0.54,从而估计数据小于11.20的可能性是54%.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
对折线图、扇形图、条形图的识读
例2某中学初中部共有120名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )
A.128 B.144 C.174 D.167
分析根据女教师的百分比,分别计算初中部和高中部女教师的人数即可.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:B
解析:初中部女教师有120×70%=84(人),高中部女教师有150×(1-60%)=150×40%=60(人),则女教师共有84+60=144(人).
反思感悟 对于折线图、扇形图、条形图一定要注意每种图示的作用和含义,其次要看清所标记数据和单位,最后要抓住各种图示中所体现的信息“密码”.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练2调查机构对某高科技行业进行调查统计,得到该行业从业者学历分布扇形图、从事该行业岗位分布条形图,如图所示.
给出下列三种说法:①该高科技行业从业人员中学历为博士的占一半以上;②该高科技行业中从事技术岗位的人数超过总人数的30%;③该高科技行业中从事运营岗位的人员主要是本科生.其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:C
解析:在①中,由该行业从业者学历分布扇形图知该高科技行业从业人员中学历为博士的占55%,故①正确;
在②中,由从事该行业岗位分布条形图知该高科技行业中从事技术岗位的人数占39.6%,超过总人数的30%,故②正确;
在③中,由题中的两个图无法得到从事运营岗位的人员主要是本科生,故③错误.故选C.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
频率分布直方图中的相关计算问题
例3在某次数学测验后,将参加考试的500名学生的数学成绩制成频率分布直方图(如图),则在该次测验中成绩不低于100分的学生人数是( )
A.210 B.205 C.200 D.195
分析由频率分布直方图先求出在该次测验中成绩不低于100分的学生的频率,由此能求出在该次测验中成绩不低于100分的学生人数.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:C
解析:由频率分布直方图,得在该次测验中成绩不低于100分的学生的频率为1-(0.012+0.018+0.030)×10=0.4,
∴在该次测验中成绩不低于100分的学生人数为500×0.4=200.故选C.
反思感悟 1.因为小长方形的面积=组距× =频率,所以各小长方形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
2.在频率分布直方图中,各小长方形的面积之和等于1.
4.在频率分布直方图中,各长方形的面积之比等于频率之比,各长方形的高度之比也等于频率之比.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
延伸探究在例3中若将“不低于100分”改为“不高于120分”结论又如何
解:由图可知成绩不高于120分的频率为1-0.006×10=1-0.06=0.94.
∴满足要求的学生人数为500×0.94=470(人).
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练3如图所示是由总体的一个样本绘制的频率分布直方图,且在[15,18)内频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33)内的频数.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:由样本频率分布直方图可知组距为3.
(3)在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47.又因为在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
总体百分数的应用
例4有一样本的数据为3310,3355,3450,3480,3490,3520,3540,3550,3650,3730,3925,求这组数据的第50百分位数和第75百分位数.
解:(1)∵i=50%×11=5.5,
∴第50百分位数是第6项的值3520.
(2)∵i=0.75×11= =8.25,
∴第75百分位数是第9项的值,即3650.所以第50百分位数和第75百分位数分别为3520,3650.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
反思感悟 1.可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
2.若题目与统计图表相联系,且各个数据信息不太清晰时,则要根据比例进行估算.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练4为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数和第75百分位数吗
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:由题意知分别落在各区间上的频数为
在[80,90)上有60×0.15=9,
在[90,100)上有60×0.25=15,
在[100,110)上有60×0.3=18,
在[110,120)上有60×0.2=12,
在[120,130]上有60×0.1=6.
从以上数据可知第50百分位数一定落在区间[100,110)上,
综上可知,第50百分位数和第75百分位数分别估计为103.3 cm,112.5 cm.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
不能正确理解频率分布直方图中纵轴的意义致错
典例有同型号的汽车100辆,为了了解这种汽车的耗油情况,现从中随机抽取10辆在同一条件下进行耗油1 L 所行驶路程的试验,得到的数据(单位:km)频率分布表如下:
试画出频率分布直方图.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
错解频率分布直方图如图所示:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
正解频率分布直方图如图所示:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
1.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60 C.120 D.140
答案:D
解析:自习时间不少于22.5小时为后三组,其频率和为(0.16+0.08+0.04)×2.5=0.7,故人数为200×0.7=140,选D.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
2.某公司2018年在各个项目中总投资500万元,如图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占 ,那么不少于3万元的项目投资共有( )
A.56万元 B.65万元 C.91万元 D.147万元
答案:B
探究一
探究二
探究三
探究四
思维辨析
随堂演练
3.对“小康县”的经济评价标准如下:
①年人均收入不小于7 000元;
②年人均食品支出不大于收入的35%.某县有40万人,调查数据如下:
则该县( )
A.是小康县
B.达到标准①,未达到标准②,不是小康县
C.达到标准②,未达到标准①,不是小康县
D.两个标准都未达到,不是小康县
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:B
解析:由图表可知全县年人均收入为7 050>7 000,达到了标准①;全县年人均食品支出为2 695,而年人均食品支出占收入的
×100%≈38.2%>35%,未达到标准②,所以不是小康县.故选B.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
4.已知有8个样本数据分别为4,7,8,11,13,15,20,22,则估计该组数据的总体的第三四分位数为 .
答案:17.5
解析:第三四分位数也就是第75百分位数,因此可得 =17.5.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
5.一个容量为100的样本,其数据的分组与各组的频数如下表:
则样本数据落在[10,40)上的频率为 .
答案:0.52
解析:样本数据落在[10,40)上频数为13+24+15=52.
则样本数据落在[10,40)上的频率为 =0.52.
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
一
二
三
四
一、频数与频率
1.将一批数据按要求分为若干个组,各组内数据的个数叫做该组的频数.每组数据的频数除以全体数据的个数的商叫做该组数据的频率.频率反映各个小组数据在样本中所占比例的大小.
2.做一做
容量为100的样本数据被分为6组,如表:
第5组的频率是( )
A.0.15 B.0.16 C.0.18 D.0.20
答案:B
解析:由表可知,第5组的频数为100-14-17-18-20-15=16,∴第5组的频率为 =0.16.故选B.
一
二
三
四
二、频率分布表
1.思考
(1)我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 你认为为了较为合理地确定出这个标准需要做哪些工作
提示a定为大部分居民的月均用水量比较合理.为了制定一个较为合理的标准a,必须先了解全市居民日常用水量的分布情况,比如月均用水量在哪个范围的居民最多,他们占全市居民的百分比情况等.
一
二
三
四
(2)一般地,列出一组样本数据的频率分布表可以分哪几个步骤进行
提示第一步,求极差.
第二步,决定组距与组数.
第三步,确定分组点,将数据分组.
第四步,列频率分布表.
一
二
三
四
(3)你能列出下列100个数据的频率分布表吗
100位居民的月均用水量(单位:t)
一
二
三
四
提示100位居民月均用水量的频率分布表如表所示.
一
二
三
四
2.填空
为了能直观地显示样本的频率分布情况,通常将样本量、样本中出现该事件的频数以及计算所得的相应频率列在一张表中,这张表叫做频率分布表.
一
二
三
四
三、频率分布直方图
1.思考
(1)为了将频率分布表中的结果直观形象地表现出来,常画出频率分布直方图.画图时,应以横轴表示分组、纵轴表示各组频率与组距的比值,以各个组距为底,以各频率除以组距的商为高,画成小长方形,这样得到的直方图就是频率分布直方图.
(2)为了直观反映样本数据在各组中的分布情况,你能根据上面的频率分布表画出频率分布直方图吗
提示频率分布直方图为:
一
二
三
四
(3)绘制频率分布直方图的步骤.
提示
一
二
三
四
2.做一做
(1)在样本频率分布直方图中,某个小长方形的面积是其他小长方形的面积之和的14,已知样本量是80,则该组的频数为( )
A.20 B.16 C.30 D.35
答案:B
解析:设该组的频数为x,则其他组的频数之和为4x,由样本量是80,得x+4x=80,解得x=16,即该组的频数为16,故选B.
一
二
三
四
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①频率分布直方图中的纵轴表示频率.( )
②频率分布直方图中每个小长方形的面积等于相应组的频率.( )
③频率分布直方图中所有小长方形的面积和等于1.( )
答案:①× ②√ ③√
一
二
三
四
四、第p百分位数
1.思考
现有一组数据3.1,2.4,2.0,1.6,1.8.
则这组数据的中位数是多少 第50百分位数是多少 若数据变为3.1,2.4,2.0,1.6结论又如何 你能发现其中的规律吗
提示第一组数据的中位数为2.0,第50百分位数2.0;
第二组数据的中位数为2.2,第50百分位数为2.2.
从以上过程可以归纳出一组数据的中位数其实就是第50百分位数.
一
二
三
四
2.填空
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
一
二
三
四
3.做一做
(1)数据1,3,8,5的中位数是 ,第50百分位数是 ,第75百分位数是 .
答案:4 4 6.5
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①任何一组数据的第50百分位数与中位数的值是相同的.( )
②第25百分位数也可以称为第一四分位数或上四分位数.( )
答案:①√ ②×
探究一
探究二
探究三
探究四
思维辨析
随堂演练
频率分布直方图的绘制与应用
例1一个农技站为了考察某种麦穗长的分布情况,在一块试验地里抽取了100个麦穗,量得长度如下(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
探究一
探究二
探究三
探究四
思维辨析
随堂演练
根据上面的数据列出频率分布表、绘出频率分布直方图,并估计长度在[5.75,6.05)cm之间的麦穗在这批麦穗中所占的百分比.
分析依据步骤画出频率分布直方图;用样本中的百分比(即频率)来估计长度在[5.75,6.05)cm之间的麦穗在这批麦穗中所占的百分比.
解:步骤是:
(1)计算极差,7.4-4.0=3.4(cm).
(2)决定组距与组数.
若取组距为0.3 cm,由于 ,需分成12组,组数合适.于是取定组距为0.3 cm,组数为12.
(3)将数据分组.
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点.则所分的12个小组可以是[3.95,4.25),[4.25,4.55),[4.55,4.85),…,[7.25,7.55].
探究一
探究二
探究三
探究四
思维辨析
随堂演练
(4)列频率分布表.
对各个小组作频数累计,然后数频数,算频率,列频率分布表,如下表所示:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
探究一
探究二
探究三
探究四
思维辨析
随堂演练
(5)画频率分布直方图,如图.
从表中看到,样本数据落在[5.75,6.05)之间的频率是0.28,于是可以估计,在这块地里,长度在[5.75,6.05)cm之间的麦穗约占28%.
反思感悟 本题画频率分布直方图时,小长方形的高易错用该组的频率的大小来表示.其原因是不清楚频率分布直方图纵轴的意义.由于画频率分布直方图的步骤比较烦琐,因此在实际操作的过程中要有足够的耐心.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练1为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组情况与频数如下:
[10.75,10.85),3;[10.85,10.95),9;[10.95,11.05),13;[11.05,11.15),16;[11.15,11.25),26;[11.25,11.35),20;[11.35,11.45),7;[11.45,11.55),4;[11.55,11.65],2.
(1)列出频率分布表;
(2)画出频率分布直方图以及频率分布折线图;
(3)根据上述图表,估计数据落在[10.95,11.35)范围内的可能性是百分之几;
(4)估计数据小于11.20的可能性是百分之几.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)频率分布表如下:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
(2)频率分布直方图及频率分布折线图如图:
(3)由上述图表可知数据落在[10.95,11.35)范围内的频率为0.13+0.16+0.26+0.20=0.75=75%,即数据落在[10.95,11.35)范围内的可能性是75%.
(4)数据小于11.20的可能性即数据小于11.20的频率,设为x,则(x-0.41)÷(11.20-11.15)=(0.67-0.41)÷(11.25-11.15),所以x-0.41=0.13,即x=0.54,从而估计数据小于11.20的可能性是54%.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
对折线图、扇形图、条形图的识读
例2某中学初中部共有120名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )
A.128 B.144 C.174 D.167
分析根据女教师的百分比,分别计算初中部和高中部女教师的人数即可.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:B
解析:初中部女教师有120×70%=84(人),高中部女教师有150×(1-60%)=150×40%=60(人),则女教师共有84+60=144(人).
反思感悟 对于折线图、扇形图、条形图一定要注意每种图示的作用和含义,其次要看清所标记数据和单位,最后要抓住各种图示中所体现的信息“密码”.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练2调查机构对某高科技行业进行调查统计,得到该行业从业者学历分布扇形图、从事该行业岗位分布条形图,如图所示.
给出下列三种说法:①该高科技行业从业人员中学历为博士的占一半以上;②该高科技行业中从事技术岗位的人数超过总人数的30%;③该高科技行业中从事运营岗位的人员主要是本科生.其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:C
解析:在①中,由该行业从业者学历分布扇形图知该高科技行业从业人员中学历为博士的占55%,故①正确;
在②中,由从事该行业岗位分布条形图知该高科技行业中从事技术岗位的人数占39.6%,超过总人数的30%,故②正确;
在③中,由题中的两个图无法得到从事运营岗位的人员主要是本科生,故③错误.故选C.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
频率分布直方图中的相关计算问题
例3在某次数学测验后,将参加考试的500名学生的数学成绩制成频率分布直方图(如图),则在该次测验中成绩不低于100分的学生人数是( )
A.210 B.205 C.200 D.195
分析由频率分布直方图先求出在该次测验中成绩不低于100分的学生的频率,由此能求出在该次测验中成绩不低于100分的学生人数.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:C
解析:由频率分布直方图,得在该次测验中成绩不低于100分的学生的频率为1-(0.012+0.018+0.030)×10=0.4,
∴在该次测验中成绩不低于100分的学生人数为500×0.4=200.故选C.
反思感悟 1.因为小长方形的面积=组距× =频率,所以各小长方形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
2.在频率分布直方图中,各小长方形的面积之和等于1.
4.在频率分布直方图中,各长方形的面积之比等于频率之比,各长方形的高度之比也等于频率之比.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
延伸探究在例3中若将“不低于100分”改为“不高于120分”结论又如何
解:由图可知成绩不高于120分的频率为1-0.006×10=1-0.06=0.94.
∴满足要求的学生人数为500×0.94=470(人).
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练3如图所示是由总体的一个样本绘制的频率分布直方图,且在[15,18)内频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33)内的频数.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:由样本频率分布直方图可知组距为3.
(3)在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47.又因为在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
总体百分数的应用
例4有一样本的数据为3310,3355,3450,3480,3490,3520,3540,3550,3650,3730,3925,求这组数据的第50百分位数和第75百分位数.
解:(1)∵i=50%×11=5.5,
∴第50百分位数是第6项的值3520.
(2)∵i=0.75×11= =8.25,
∴第75百分位数是第9项的值,即3650.所以第50百分位数和第75百分位数分别为3520,3650.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
反思感悟 1.可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
2.若题目与统计图表相联系,且各个数据信息不太清晰时,则要根据比例进行估算.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练4为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数和第75百分位数吗
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:由题意知分别落在各区间上的频数为
在[80,90)上有60×0.15=9,
在[90,100)上有60×0.25=15,
在[100,110)上有60×0.3=18,
在[110,120)上有60×0.2=12,
在[120,130]上有60×0.1=6.
从以上数据可知第50百分位数一定落在区间[100,110)上,
综上可知,第50百分位数和第75百分位数分别估计为103.3 cm,112.5 cm.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
不能正确理解频率分布直方图中纵轴的意义致错
典例有同型号的汽车100辆,为了了解这种汽车的耗油情况,现从中随机抽取10辆在同一条件下进行耗油1 L 所行驶路程的试验,得到的数据(单位:km)频率分布表如下:
试画出频率分布直方图.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
错解频率分布直方图如图所示:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
正解频率分布直方图如图所示:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
1.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60 C.120 D.140
答案:D
解析:自习时间不少于22.5小时为后三组,其频率和为(0.16+0.08+0.04)×2.5=0.7,故人数为200×0.7=140,选D.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
2.某公司2018年在各个项目中总投资500万元,如图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占 ,那么不少于3万元的项目投资共有( )
A.56万元 B.65万元 C.91万元 D.147万元
答案:B
探究一
探究二
探究三
探究四
思维辨析
随堂演练
3.对“小康县”的经济评价标准如下:
①年人均收入不小于7 000元;
②年人均食品支出不大于收入的35%.某县有40万人,调查数据如下:
则该县( )
A.是小康县
B.达到标准①,未达到标准②,不是小康县
C.达到标准②,未达到标准①,不是小康县
D.两个标准都未达到,不是小康县
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:B
解析:由图表可知全县年人均收入为7 050>7 000,达到了标准①;全县年人均食品支出为2 695,而年人均食品支出占收入的
×100%≈38.2%>35%,未达到标准②,所以不是小康县.故选B.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
4.已知有8个样本数据分别为4,7,8,11,13,15,20,22,则估计该组数据的总体的第三四分位数为 .
答案:17.5
解析:第三四分位数也就是第75百分位数,因此可得 =17.5.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
5.一个容量为100的样本,其数据的分组与各组的频数如下表:
则样本数据落在[10,40)上的频率为 .
答案:0.52
解析:样本数据落在[10,40)上频数为13+24+15=52.
则样本数据落在[10,40)上的频率为 =0.52.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
