人教A版(2019)高中数学必修第二册 课件9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计(共50张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 课件9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 11:13:16 | ||
图片预览










文档简介
(共50张PPT)
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
一
二
三
四
一、众数、中位数、平均数
1.思考
某次数学考试,婷婷得到78分.全班共30人,其他同学的成绩为1个100分,4个90分,22个80分,以及1个2分和1个10分.
(1)这30个分数的众数是多少
(2)这30个分数的中位数是多少
(3)婷婷计算出平均分为77,她对妈妈说这次成绩处在“中上水平”,你觉得婷婷说的对吗
提示(1)80 (2)80
(3)婷婷的说法不确切,由于受两个极端分数影响导致平均数明显下降,而婷婷的成绩实际是倒数第三名.
一
二
三
四
2.填空
(1)众数
①定义:一组数据中出现次数最多的数据(即频率分布最大值所对应的样本数据)称为这组数据的众数.
②特征:一组数据中的众数可能不止一个,也可能没有,反映了该组数据的集中趋势.
(2)中位数
①定义:一组数据按从小到大(或从大到小)的顺序排成一列,处于最中间的一个数据(当数据个数是奇数时)或最中间两个数据的平均数(当数据个数是偶数时)称为这组数据的中位数.
②特征:一组数据中的中位数是唯一的,反映了该组数据的集中趋势.在频率分布直方图中,中位数左边和右边的直方图的面积相等.
一
二
三
四
(3)平均数
①定义:一组数据的和与这组数据的个数的商.数据x1,x2,…,xn的
②特征:平均数对数据有“取齐”的作用,代表该组数据的平均水平,任何一个数据的改变都会引起平均数的变化,这是众数和中位数都不具有的性质.所以与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中极端值的影响较大,使平均数在估计总体时的可靠性降低.
一
二
三
四
名师归纳 三种数字特征的优缺点
一
二
三
四
3.做一做
(1)10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c B.b>c>a
C.c>a>b D.c>b>a
答案:D
解析:将数据从小到大排列为10,12,14,14,15,15,16,17,17,17,则平均数a= ×(10+12+14×2+15×2+16+17×3)=14.7,中位数b=15,众数c=17,显然a一
二
三
四
(2)有一组数据,其中10,12,13,15,16出现的频率分别是0.15,0.2,0.3,0.2,0.15,则该组数据的平均数为 .
答案:13.2
解析:该组数据的平均数为10×0.15+12×0.2+13×0.3+15×0.2+16×0.15=13.2.
(3)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①一组数据的众数可以是1个或几个,也可以没有.( )
②一组数据的中位数可能不存在.( )
③样本量越小,样本平均数越接近总体平均数.( )
答案:①√ ②× ③×
一
二
三
四
二、探索图表中的中位数与平均数数值规律
1.思考
(1)如何在样本数据的频率分布直方图中估计出平均数的值
提示平均数是频率分布直方图的“重心”,是直方图的平衡点,因此,每个小矩形的面积与小矩形底边中点的横坐标的乘积之和即为平均数的估计值.
一
二
三
四
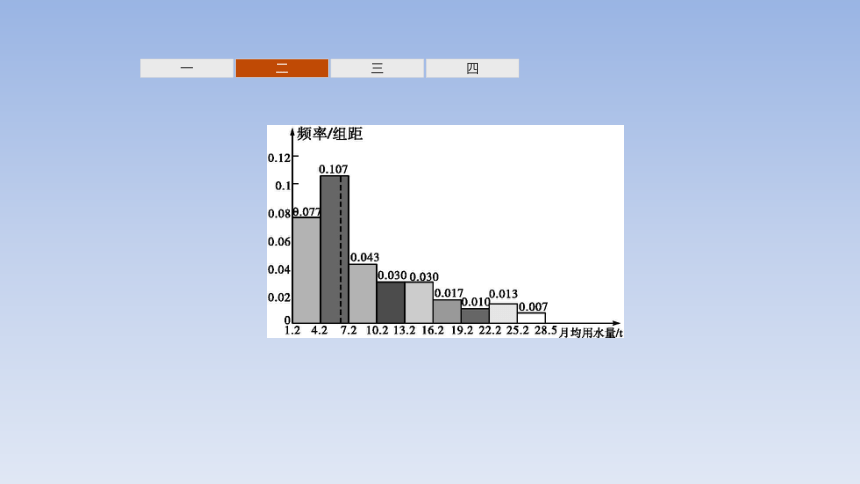
(2)如何在样本数据的频率分布直方图中,估计出中位数的值 你能利用在上一节中调查的100位居民的月均用水量的频率分布直方图加以说明吗
提示根据中位数的意义,在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.由于0.077×3=0.231,(0.077+0.107)×3=0.552.因此中位数落在区间[4.2,7.2)内.设中位数为x,由0.077×3+0.107×(x-4.2)=0.5,得到x≈6.71.因此,中位数约为6.71,如图所示.这个结果与根据原始数据求得的中位数6.6相差不大.
一
二
三
四
一
二
三
四
2.填空
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在下图的三种分布形态中,平均数和中位数的大小存在什么关系
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的(图1),那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”(图2),那么平均数大于中位数;如果直方图在左边“拖尾”(图3),那么平均数小于中位数.也就是说,和中位数相比,平均数总是在“长尾巴”那边.
一
二
三
四
3.做一做
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是4月9日
C.这12天的AQI指数值的中位数是90
D.从4日到9日,空气质量越来越好
一
二
三
四
答案:C
解析:这12天中,空气质量为“优良”的有95,85,77,67,72,92,共6天,故A正确;这12天中空气质量最好的是4月9日,AQI指数值为67,故B正确;这12天的AQI指数值的中位数是 =99.5,故C不正确;从4日到9日,AQI指数值越来越小,表示空气质量越来越好,故D正确.故选C.
一
二
三
四
三、方差、标准差
1.思考
(1)平均数向我们提供了样本数据的重要信息,但是,平均数有时也会使我们作出对总体的片面判断,因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽视的.因此,只用平均数还难以概括样本数据的实际状态.如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
如果你是教练,你应当如何对这次射击作出评价
一
二
三
四
如果你是教练,你应当如何对这次射击作出评价
①甲、乙两人本次射击的平均成绩分别为多少环 他们的平均成绩一样吗
一
二
三
四
②难道这两个人的水平就没有什么差异了吗 你能作出这两人成绩的频率分布条形图来说明其水平差异在哪里吗
提示频率分布条形图如下:
(甲)
(乙)
从图上可以直观地看出,他们的水平还是有差异的,甲成绩比较分散,乙成绩相对集中.
一
二
三
四
(2)现实中的总体所包含的个体数往往是很多的,总体的平均数与标准差是不知道的.如何求得总体的平均数和标准差呢
提示通常的做法是用样本的平均数和标准差去估计总体的平均数与标准差.这与前面用样本的频率分布来近似地代替总体分布是类似的.只要样本的代表性好,这样做就是合理的,也是可以接受的.
一
二
三
四
一
二
三
四
一
二
三
四
归纳提升 对标准差和方差的理解
(1)样本标准差反映了各样本数据聚集于样本平均数周围的程度,标准差越小,表明各个样本数据在样本平均数周围越集中;反之,标准差越大,表明各样本数据在样本平均数的周围越分散.
(2)若样本数据都相等,则s=0.
(3)当样本的平均数相等或相差无几时,就要用样本数据的离散程度来估计总体的数字特征,而样本数据的离散程度,就由标准差来衡量.
(4)数据的离散程度可以通过极差、方差或标准差来描述.极差反映了一组数据变化的最大幅度,它对一组数据中的极端值非常敏感;方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常用标准差——样本方差的算术平方根来描述.
一
二
三
四
(5)标准差的大小不会越过极差.
(6)方差、标准差、极差的取值范围为[0,+∞).当标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性.
(7)因为方差与原始数据的单位不同,且平方后可能夸大了偏差的程度,所以虽然方差和标准差在刻画样本数据的分散程度上是一样的,但在解决实际问题时,一般采用标准差.
(8)在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
一
二
三
四
3.做一做
(1)对划艇运动员甲、乙在相同的条件下进行了6次测试,测得他们每次的最大速度(单位:m/s)如下:
甲:27,38,30,37,35,31
乙:33,29,38,34,28,36
根据以上数据,试判断他们谁更优秀.
一
二
三
四
一
二
三
四
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.( )
②若两组数据的方差一样大,则说明这两组数据都是相同的.( )
答案:①√ ②×
一
二
三
四
四、有关平均数、方差的重要结论
1.思考
若x1,x2,…,xn的方差是s2,则ax1,ax2,…,axn的方差是多少
提示由方差的定义知ax1,ax2,…,axn的方差是a2s2.
2.填空
(1)若x1,x2,…,xn的平均数是 ,则mx1+a,mx2+a,…,mxn+a的平均数是 .
(2)数据x1,x2,…,xn与数据x1+a,x2+a,…xn+a的方差相等.
(3)若x1,x2,…,xn的方差为s2,则ax1,ax2,…,axn的方差为a2s2.
一
二
三
四
3.做一做
已知样本数据x1,x2,…,xn的平均数 =5,s2=2,则样本数据2x1+1,2x2+1,…,2xn+1的平均数为 ,方差为 .
答案:11 8
解析:因为样本数据x1,x2,…,xn的平均数 =5,所以样本数据2x1+1,2x2+1,…,2xn+1的平均数为2 +1=2×5+1=11.方差为22×s2=4×2=8.
探究一
探究二
探究三
思维辨析
随堂演练
众数、中位数、平均数的应用
例1某公司的33名人员的月工资如下:
(1)求该公司人员月工资的平均数、中位数、众数(精确到元);
(2)假设副董事长的工资从20 000元提升到30 000元;董事长的工资从30 000元提升到50 000元,那么新的平均数、中位数、众数又是什么 (精确到元)
(3)你认为哪个统计量更能反映这个公司人员的工资水平 结合此问题谈一谈你的看法.
分析平均数定义→计算平均数→将数据从小到大排列→得中位数、众数→结论
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)平均数是 =(30 000+20 000+15 000×2+10 000+8 000×5+6 000×3+4 500×20)÷33≈7 212(元),
中位数是4 500元,众数是4 500元.
(2)平均数是 '=(50 000+30 000+15 000×2+10 000+8 000×5+6 000×3+4 500×20)÷33≈8 121(元),中位数是4 500元,众数是4 500元.
(3)在这个问题中,中位数和众数均能反映该公司人员的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数偏差较大,所以平均数不能反映这个公司人员的工资水平.
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.深刻理解和把握平均数、中位数、众数在反映样本数据上的特点,并结合实际情况,灵活应用.
2.如果样本平均数大于样本中位数,说明数据中存在许多较大的极端值;反之,说明数据中存在许多较小的极端值.在实际应用中,如果同时知道样本中位数和样本平均数,可以使我们了解样本数据中极端数据的信息,帮助我们作出决策.
3.平均数对极端值敏感,而中位数对极端值不敏感.因此两者结合,可较好地分析总体的情况.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练1从某中学高三年级甲、乙两个班各选出7名学生参加数学竞赛,他们取得的成绩(满足100分)如下:
甲:79 78 80 x 85 92 96
乙:72 81 81 y 91 91 96
其中甲班学生成绩的平均分和乙班学生成绩的中位数都是85,则x+y的值为( )
A.152 B.168 C.190 D.170
答案:D
解析:由数据知,乙班成绩的中位数是y=85.
又甲班学生成绩的平均分为85,即79+78+80+x+85+92+96=85×7,解得x=85,∴x+y=170.故选D.
探究一
探究二
探究三
思维辨析
随堂演练
平均数与方差的性质与应用
(2)甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
①分别计算两组数据的平均数及方差;
②根据计算结果判断哪台机床加工零件的质量更稳定.
分析求平均数→求方差s2
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 在实际问题中,仅靠平均数不能完全反映问题,还要研究其偏离平均值的离散程度(即方差或标准差):方差大说明取值分散性大,数值不稳定;方差小说明取值分散性小,数值集中、稳定.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练2一组数据的平均数是2.8,标准差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和标准差分别为( )
A.57.2 3.6 B.57.2 56.4
C.62.8 63.6 D.62.8 3.6
答案:D
解析:一组数据中的每一个数据都加上60后,新数据的平均数也增加60,即为2.8+60=62.8,而标准差保持不变,仍为3.6.
探究一
探究二
探究三
思维辨析
随堂演练
频率分布直方图(频率分布折线图)中的“隐藏”的数据信息
例3如图为学生身高频率分布直方图.
(1)如何在样本数据的频率分布直方图中估计出众数的值
(2)如何在样本数据的频率分布直方图中估计出中位数的值
(3)如何在样本数据的频率分布直方图中估计出平均数的值
(4)从样本数据可知,该样本的众数是166 cm,172 cm,中位数是171 cm,平均数是170.1 cm,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)众数大致的值就是样本数据的频率分布直方图中最高小长方形的中点的横坐标.由直方图可估计学生身高众数应为174.5 cm.
(2)在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数使得在它左边和右边的直方图的面积相等,由此可以估计中位数的值,如图,由于0.08+0.22=0.3,0.08+0.22+0.22=0.52,所以中位数落在区间[167,172)内.
设中位数是x,由0.08+0.22+(x-167)× =0.5,解得x≈171.55.所以学生身高的中位数约为171.55 cm.
探究一
探究二
探究三
思维辨析
随堂演练
(3)平均数是频率分布直方图的“重心”,是频率分布直方图的平衡点,因此,每个小长方形的面积与小长方形底边中点的横坐标的乘积之和为平均数.由159.5×0.08+164.5×0.22+169.5×0.22+174.5×0.36+179.5×0.12=170.6,得学生身高的平均数为170.6 cm.
(4)因为样本数据频率分布直方图只是直观地表明分布的形状,从直方图本身得不出原始的数据内容,也就是说频率分布直方图损失了一些样本数据的信息,得到的是一个估计值,且所得估计值与数据分组有关,所以估计的值有一定的偏差.
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.利用直方图或折线图求得的众数、中位数、平均数均为近似值,往往与实际数据得出的不一致.但它们能粗略估计其众数、中位数和平均数.
2.利用频率分布直方图求数字特征:
(1)众数是最高小长方形的底边中点的横坐标;
(2)中位数使得在它左、右两侧直方图的面积相等;
(3)平均数等于每个小长方形的面积乘小长方形底边中点的横坐标之和.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练3甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
请从下列四个不同的角度对这次测试结果进行分析.
(1)从平均数和方差相结合看(分析谁的成绩好些);
(2)从平均数和中位数相结合看(分析谁的成绩好些);
(3)从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
(4)从折线图上两人射击命中环数的走势看(分析谁更有潜力).
探究一
探究二
探究三
思维辨析
随堂演练
解:根据各问情况作如下统计表.
∴甲的成绩比乙好.
(2)∵平均数相同,甲的中位数<乙的中位数,
∴乙的成绩比甲好.
(3)∵平均数相同,且乙命中9环及9环以上次数比甲多,∴乙的成绩比甲好.
(4)∵甲的成绩在平均线上下波动;而乙处于上升趋势,从第四次以后就没有比甲少的情况发生,
∴乙更有潜力.
探究一
探究二
探究三
思维辨析
随堂演练
1.找齐法
在计算平均数时,如果这些数字都在某个数字左右摆动,就选取一个数字作为标准进行找齐.
典例1计算数据87,86,90,82,83,85,88,80,79,90的平均数和方差.
分析这组数据都在85左右摆动,把每个数字都减去85后进行计算.
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
典例2计算数据54,55,53,56,57,58的方差.
分析可以根据简化公式进行计算,也可以把每个数据减去一个数,用找齐法计算.
归纳提升方差反映的是数据组偏离平均值的程度,因此把数据组中的每一个数据都加上或者都减去一个相同的数不影响方差的大小,当我们计算的数据较大时,这个方法能有效地简化运算.
探究一
探究二
探究三
思维辨析
随堂演练
1.一组样本数据按从小到大的顺序排列为13,14,19,x,23,27,28,31,其中位数为22,则x等于( )
A.21 B.22 C.20 D.23
答案:A
解析:根据题意知,中位数22= ,则x=21.
探究一
探究二
探究三
思维辨析
随堂演练
2.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别是x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.x1,x2,…,xn的平均值 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
答案:B
解析:在A中,平均数是表示一组数据集中趋势的量,它是反映数据集中趋势的一项指标,故A不可以用来评估这种农作物亩产量的稳定程度;在B中,标准差能反映一组数据的离散程度,故B可以用来评估这种农作物亩产量的稳定程度;在C中,最大值是一组数据中最大的量,故C不可以用来评估这种农作物亩产量的稳定程度;在D中,中位数将数据分成前半部分和后半部分,用来代表一组数据的“中等水平”,故D不可以用来评估这种农作物亩产量的稳定程度,故选B.
探究一
探究二
探究三
思维辨析
随堂演练
3.样本中共有五个个体,其值分别为a,0,1,2,3.若该样本的平均值为1,则样本的方差为( )
答案:D
探究一
探究二
探究三
思维辨析
随堂演练
4.(多选)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则以下选项判断不正确的有( )
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
答案:ABD
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
5.甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:
若要从这四人中选择一人去参加该运动会射击项目比赛,最佳人选是 .(填“甲”“乙”“丙”“丁”中的一个)
答案:丙
解析:分析表格数据可知,乙与丙的平均环数最多,又丙的方差比乙小,说明丙成绩发挥得较为稳定,所以最佳人选为丙.
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
一
二
三
四
一、众数、中位数、平均数
1.思考
某次数学考试,婷婷得到78分.全班共30人,其他同学的成绩为1个100分,4个90分,22个80分,以及1个2分和1个10分.
(1)这30个分数的众数是多少
(2)这30个分数的中位数是多少
(3)婷婷计算出平均分为77,她对妈妈说这次成绩处在“中上水平”,你觉得婷婷说的对吗
提示(1)80 (2)80
(3)婷婷的说法不确切,由于受两个极端分数影响导致平均数明显下降,而婷婷的成绩实际是倒数第三名.
一
二
三
四
2.填空
(1)众数
①定义:一组数据中出现次数最多的数据(即频率分布最大值所对应的样本数据)称为这组数据的众数.
②特征:一组数据中的众数可能不止一个,也可能没有,反映了该组数据的集中趋势.
(2)中位数
①定义:一组数据按从小到大(或从大到小)的顺序排成一列,处于最中间的一个数据(当数据个数是奇数时)或最中间两个数据的平均数(当数据个数是偶数时)称为这组数据的中位数.
②特征:一组数据中的中位数是唯一的,反映了该组数据的集中趋势.在频率分布直方图中,中位数左边和右边的直方图的面积相等.
一
二
三
四
(3)平均数
①定义:一组数据的和与这组数据的个数的商.数据x1,x2,…,xn的
②特征:平均数对数据有“取齐”的作用,代表该组数据的平均水平,任何一个数据的改变都会引起平均数的变化,这是众数和中位数都不具有的性质.所以与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中极端值的影响较大,使平均数在估计总体时的可靠性降低.
一
二
三
四
名师归纳 三种数字特征的优缺点
一
二
三
四
3.做一做
(1)10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c B.b>c>a
C.c>a>b D.c>b>a
答案:D
解析:将数据从小到大排列为10,12,14,14,15,15,16,17,17,17,则平均数a= ×(10+12+14×2+15×2+16+17×3)=14.7,中位数b=15,众数c=17,显然a
二
三
四
(2)有一组数据,其中10,12,13,15,16出现的频率分别是0.15,0.2,0.3,0.2,0.15,则该组数据的平均数为 .
答案:13.2
解析:该组数据的平均数为10×0.15+12×0.2+13×0.3+15×0.2+16×0.15=13.2.
(3)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①一组数据的众数可以是1个或几个,也可以没有.( )
②一组数据的中位数可能不存在.( )
③样本量越小,样本平均数越接近总体平均数.( )
答案:①√ ②× ③×
一
二
三
四
二、探索图表中的中位数与平均数数值规律
1.思考
(1)如何在样本数据的频率分布直方图中估计出平均数的值
提示平均数是频率分布直方图的“重心”,是直方图的平衡点,因此,每个小矩形的面积与小矩形底边中点的横坐标的乘积之和即为平均数的估计值.
一
二
三
四
(2)如何在样本数据的频率分布直方图中,估计出中位数的值 你能利用在上一节中调查的100位居民的月均用水量的频率分布直方图加以说明吗
提示根据中位数的意义,在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.由于0.077×3=0.231,(0.077+0.107)×3=0.552.因此中位数落在区间[4.2,7.2)内.设中位数为x,由0.077×3+0.107×(x-4.2)=0.5,得到x≈6.71.因此,中位数约为6.71,如图所示.这个结果与根据原始数据求得的中位数6.6相差不大.
一
二
三
四
一
二
三
四
2.填空
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在下图的三种分布形态中,平均数和中位数的大小存在什么关系
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的(图1),那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”(图2),那么平均数大于中位数;如果直方图在左边“拖尾”(图3),那么平均数小于中位数.也就是说,和中位数相比,平均数总是在“长尾巴”那边.
一
二
三
四
3.做一做
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是4月9日
C.这12天的AQI指数值的中位数是90
D.从4日到9日,空气质量越来越好
一
二
三
四
答案:C
解析:这12天中,空气质量为“优良”的有95,85,77,67,72,92,共6天,故A正确;这12天中空气质量最好的是4月9日,AQI指数值为67,故B正确;这12天的AQI指数值的中位数是 =99.5,故C不正确;从4日到9日,AQI指数值越来越小,表示空气质量越来越好,故D正确.故选C.
一
二
三
四
三、方差、标准差
1.思考
(1)平均数向我们提供了样本数据的重要信息,但是,平均数有时也会使我们作出对总体的片面判断,因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽视的.因此,只用平均数还难以概括样本数据的实际状态.如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
如果你是教练,你应当如何对这次射击作出评价
一
二
三
四
如果你是教练,你应当如何对这次射击作出评价
①甲、乙两人本次射击的平均成绩分别为多少环 他们的平均成绩一样吗
一
二
三
四
②难道这两个人的水平就没有什么差异了吗 你能作出这两人成绩的频率分布条形图来说明其水平差异在哪里吗
提示频率分布条形图如下:
(甲)
(乙)
从图上可以直观地看出,他们的水平还是有差异的,甲成绩比较分散,乙成绩相对集中.
一
二
三
四
(2)现实中的总体所包含的个体数往往是很多的,总体的平均数与标准差是不知道的.如何求得总体的平均数和标准差呢
提示通常的做法是用样本的平均数和标准差去估计总体的平均数与标准差.这与前面用样本的频率分布来近似地代替总体分布是类似的.只要样本的代表性好,这样做就是合理的,也是可以接受的.
一
二
三
四
一
二
三
四
一
二
三
四
归纳提升 对标准差和方差的理解
(1)样本标准差反映了各样本数据聚集于样本平均数周围的程度,标准差越小,表明各个样本数据在样本平均数周围越集中;反之,标准差越大,表明各样本数据在样本平均数的周围越分散.
(2)若样本数据都相等,则s=0.
(3)当样本的平均数相等或相差无几时,就要用样本数据的离散程度来估计总体的数字特征,而样本数据的离散程度,就由标准差来衡量.
(4)数据的离散程度可以通过极差、方差或标准差来描述.极差反映了一组数据变化的最大幅度,它对一组数据中的极端值非常敏感;方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常用标准差——样本方差的算术平方根来描述.
一
二
三
四
(5)标准差的大小不会越过极差.
(6)方差、标准差、极差的取值范围为[0,+∞).当标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性.
(7)因为方差与原始数据的单位不同,且平方后可能夸大了偏差的程度,所以虽然方差和标准差在刻画样本数据的分散程度上是一样的,但在解决实际问题时,一般采用标准差.
(8)在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
一
二
三
四
3.做一做
(1)对划艇运动员甲、乙在相同的条件下进行了6次测试,测得他们每次的最大速度(单位:m/s)如下:
甲:27,38,30,37,35,31
乙:33,29,38,34,28,36
根据以上数据,试判断他们谁更优秀.
一
二
三
四
一
二
三
四
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.( )
②若两组数据的方差一样大,则说明这两组数据都是相同的.( )
答案:①√ ②×
一
二
三
四
四、有关平均数、方差的重要结论
1.思考
若x1,x2,…,xn的方差是s2,则ax1,ax2,…,axn的方差是多少
提示由方差的定义知ax1,ax2,…,axn的方差是a2s2.
2.填空
(1)若x1,x2,…,xn的平均数是 ,则mx1+a,mx2+a,…,mxn+a的平均数是 .
(2)数据x1,x2,…,xn与数据x1+a,x2+a,…xn+a的方差相等.
(3)若x1,x2,…,xn的方差为s2,则ax1,ax2,…,axn的方差为a2s2.
一
二
三
四
3.做一做
已知样本数据x1,x2,…,xn的平均数 =5,s2=2,则样本数据2x1+1,2x2+1,…,2xn+1的平均数为 ,方差为 .
答案:11 8
解析:因为样本数据x1,x2,…,xn的平均数 =5,所以样本数据2x1+1,2x2+1,…,2xn+1的平均数为2 +1=2×5+1=11.方差为22×s2=4×2=8.
探究一
探究二
探究三
思维辨析
随堂演练
众数、中位数、平均数的应用
例1某公司的33名人员的月工资如下:
(1)求该公司人员月工资的平均数、中位数、众数(精确到元);
(2)假设副董事长的工资从20 000元提升到30 000元;董事长的工资从30 000元提升到50 000元,那么新的平均数、中位数、众数又是什么 (精确到元)
(3)你认为哪个统计量更能反映这个公司人员的工资水平 结合此问题谈一谈你的看法.
分析平均数定义→计算平均数→将数据从小到大排列→得中位数、众数→结论
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)平均数是 =(30 000+20 000+15 000×2+10 000+8 000×5+6 000×3+4 500×20)÷33≈7 212(元),
中位数是4 500元,众数是4 500元.
(2)平均数是 '=(50 000+30 000+15 000×2+10 000+8 000×5+6 000×3+4 500×20)÷33≈8 121(元),中位数是4 500元,众数是4 500元.
(3)在这个问题中,中位数和众数均能反映该公司人员的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数偏差较大,所以平均数不能反映这个公司人员的工资水平.
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.深刻理解和把握平均数、中位数、众数在反映样本数据上的特点,并结合实际情况,灵活应用.
2.如果样本平均数大于样本中位数,说明数据中存在许多较大的极端值;反之,说明数据中存在许多较小的极端值.在实际应用中,如果同时知道样本中位数和样本平均数,可以使我们了解样本数据中极端数据的信息,帮助我们作出决策.
3.平均数对极端值敏感,而中位数对极端值不敏感.因此两者结合,可较好地分析总体的情况.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练1从某中学高三年级甲、乙两个班各选出7名学生参加数学竞赛,他们取得的成绩(满足100分)如下:
甲:79 78 80 x 85 92 96
乙:72 81 81 y 91 91 96
其中甲班学生成绩的平均分和乙班学生成绩的中位数都是85,则x+y的值为( )
A.152 B.168 C.190 D.170
答案:D
解析:由数据知,乙班成绩的中位数是y=85.
又甲班学生成绩的平均分为85,即79+78+80+x+85+92+96=85×7,解得x=85,∴x+y=170.故选D.
探究一
探究二
探究三
思维辨析
随堂演练
平均数与方差的性质与应用
(2)甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
①分别计算两组数据的平均数及方差;
②根据计算结果判断哪台机床加工零件的质量更稳定.
分析求平均数→求方差s2
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 在实际问题中,仅靠平均数不能完全反映问题,还要研究其偏离平均值的离散程度(即方差或标准差):方差大说明取值分散性大,数值不稳定;方差小说明取值分散性小,数值集中、稳定.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练2一组数据的平均数是2.8,标准差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和标准差分别为( )
A.57.2 3.6 B.57.2 56.4
C.62.8 63.6 D.62.8 3.6
答案:D
解析:一组数据中的每一个数据都加上60后,新数据的平均数也增加60,即为2.8+60=62.8,而标准差保持不变,仍为3.6.
探究一
探究二
探究三
思维辨析
随堂演练
频率分布直方图(频率分布折线图)中的“隐藏”的数据信息
例3如图为学生身高频率分布直方图.
(1)如何在样本数据的频率分布直方图中估计出众数的值
(2)如何在样本数据的频率分布直方图中估计出中位数的值
(3)如何在样本数据的频率分布直方图中估计出平均数的值
(4)从样本数据可知,该样本的众数是166 cm,172 cm,中位数是171 cm,平均数是170.1 cm,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)众数大致的值就是样本数据的频率分布直方图中最高小长方形的中点的横坐标.由直方图可估计学生身高众数应为174.5 cm.
(2)在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数使得在它左边和右边的直方图的面积相等,由此可以估计中位数的值,如图,由于0.08+0.22=0.3,0.08+0.22+0.22=0.52,所以中位数落在区间[167,172)内.
设中位数是x,由0.08+0.22+(x-167)× =0.5,解得x≈171.55.所以学生身高的中位数约为171.55 cm.
探究一
探究二
探究三
思维辨析
随堂演练
(3)平均数是频率分布直方图的“重心”,是频率分布直方图的平衡点,因此,每个小长方形的面积与小长方形底边中点的横坐标的乘积之和为平均数.由159.5×0.08+164.5×0.22+169.5×0.22+174.5×0.36+179.5×0.12=170.6,得学生身高的平均数为170.6 cm.
(4)因为样本数据频率分布直方图只是直观地表明分布的形状,从直方图本身得不出原始的数据内容,也就是说频率分布直方图损失了一些样本数据的信息,得到的是一个估计值,且所得估计值与数据分组有关,所以估计的值有一定的偏差.
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.利用直方图或折线图求得的众数、中位数、平均数均为近似值,往往与实际数据得出的不一致.但它们能粗略估计其众数、中位数和平均数.
2.利用频率分布直方图求数字特征:
(1)众数是最高小长方形的底边中点的横坐标;
(2)中位数使得在它左、右两侧直方图的面积相等;
(3)平均数等于每个小长方形的面积乘小长方形底边中点的横坐标之和.
探究一
探究二
探究三
思维辨析
随堂演练
变式训练3甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
请从下列四个不同的角度对这次测试结果进行分析.
(1)从平均数和方差相结合看(分析谁的成绩好些);
(2)从平均数和中位数相结合看(分析谁的成绩好些);
(3)从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
(4)从折线图上两人射击命中环数的走势看(分析谁更有潜力).
探究一
探究二
探究三
思维辨析
随堂演练
解:根据各问情况作如下统计表.
∴甲的成绩比乙好.
(2)∵平均数相同,甲的中位数<乙的中位数,
∴乙的成绩比甲好.
(3)∵平均数相同,且乙命中9环及9环以上次数比甲多,∴乙的成绩比甲好.
(4)∵甲的成绩在平均线上下波动;而乙处于上升趋势,从第四次以后就没有比甲少的情况发生,
∴乙更有潜力.
探究一
探究二
探究三
思维辨析
随堂演练
1.找齐法
在计算平均数时,如果这些数字都在某个数字左右摆动,就选取一个数字作为标准进行找齐.
典例1计算数据87,86,90,82,83,85,88,80,79,90的平均数和方差.
分析这组数据都在85左右摆动,把每个数字都减去85后进行计算.
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
典例2计算数据54,55,53,56,57,58的方差.
分析可以根据简化公式进行计算,也可以把每个数据减去一个数,用找齐法计算.
归纳提升方差反映的是数据组偏离平均值的程度,因此把数据组中的每一个数据都加上或者都减去一个相同的数不影响方差的大小,当我们计算的数据较大时,这个方法能有效地简化运算.
探究一
探究二
探究三
思维辨析
随堂演练
1.一组样本数据按从小到大的顺序排列为13,14,19,x,23,27,28,31,其中位数为22,则x等于( )
A.21 B.22 C.20 D.23
答案:A
解析:根据题意知,中位数22= ,则x=21.
探究一
探究二
探究三
思维辨析
随堂演练
2.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别是x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.x1,x2,…,xn的平均值 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
答案:B
解析:在A中,平均数是表示一组数据集中趋势的量,它是反映数据集中趋势的一项指标,故A不可以用来评估这种农作物亩产量的稳定程度;在B中,标准差能反映一组数据的离散程度,故B可以用来评估这种农作物亩产量的稳定程度;在C中,最大值是一组数据中最大的量,故C不可以用来评估这种农作物亩产量的稳定程度;在D中,中位数将数据分成前半部分和后半部分,用来代表一组数据的“中等水平”,故D不可以用来评估这种农作物亩产量的稳定程度,故选B.
探究一
探究二
探究三
思维辨析
随堂演练
3.样本中共有五个个体,其值分别为a,0,1,2,3.若该样本的平均值为1,则样本的方差为( )
答案:D
探究一
探究二
探究三
思维辨析
随堂演练
4.(多选)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则以下选项判断不正确的有( )
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
答案:ABD
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
5.甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:
若要从这四人中选择一人去参加该运动会射击项目比赛,最佳人选是 .(填“甲”“乙”“丙”“丁”中的一个)
答案:丙
解析:分析表格数据可知,乙与丙的平均环数最多,又丙的方差比乙小,说明丙成绩发挥得较为稳定,所以最佳人选为丙.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
