人教A版(2019)高中数学必修第二册 9.2.1(第2课时)统计图 导学案(含答案)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 9.2.1(第2课时)统计图 导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 705.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览


文档简介
9.2.1 总体取值规律的估计
第2课时 统计图
1.理解频率分布表、折线图、条形图、扇形图的作用和识读.
2.了解不同的统计图在表示数据上有不同的特点.
1.直观想象:各种统计图的理解;
2.数学运算:各种统计图的相关计算.
重点:各种统计图的相关计算.
难点:各种统计图的理解.
预习导入
阅读课本198-200页,填写。
1.常见的其他统计图:条形图、扇形图、折线图.
扇形图主要用于直观描述各类数据占总数的比例;
条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率;
折线图主要用于描述数据随时间的变化趋势.
2.各个统计图特点
(1)不同的统计图在表示数据上有不同的特点.如扇形图主要用于直观描述各类数据占总数的 ,条形图和直方图主要用于直观描述不同类别或分组数据的 和 ,折线图主要用于描述数据随时间的变化趋势.
(2)不同的统计图适用的数据类型也不同.如条形图适用于描述 的数据,直方图适用于描述 数据.
1.要反映某市一周内每天的最高气温的变化情况,宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
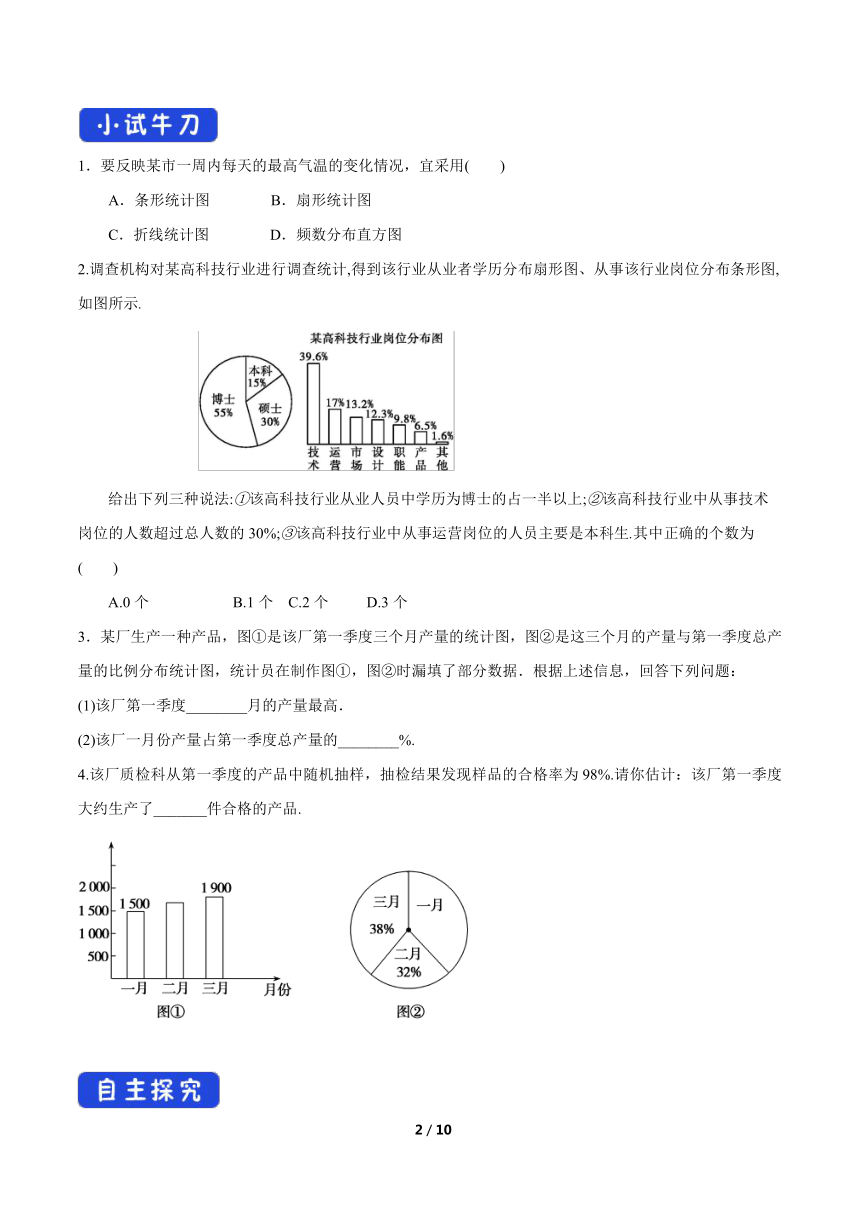
2.调查机构对某高科技行业进行调查统计,得到该行业从业者学历分布扇形图、从事该行业岗位分布条形图,如图所示.
给出下列三种说法:①该高科技行业从业人员中学历为博士的占一半以上;②该高科技行业中从事技术岗位的人数超过总人数的30%;③该高科技行业中从事运营岗位的人员主要是本科生.其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
3.某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:
(1)该厂第一季度________月的产量最高.
(2)该厂一月份产量占第一季度总产量的________%.
4.该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%.请你估计:该厂第一季度大约生产了_______件合格的产品.
题型一 对折线图、扇形图、条形图的识读
例1 已知某市2015年全年空气质量等级如表1所示.
表1
空气质量等级(空气质量指数(AQI)) 频数 频率
优(AQI≤50) 83 22.8%
良(50轻度污染(100中度污染(150重度污染(200严重污染(AQI>300) 14 3.8%
合计 365 100%
2016年5月和6月的空气质量指数如下:
5月 240 80 56 53 92 126 45 87 56 60
191 62 55 58 56 53 89 90 125 124
103 81 89 44 34 53 79 81 62 116
88
6月 63 92 110 122 102 116 81 163 158 76
33 102 65 53 38 55 52 76 99 127
120 80 108 33 35 73 82 90 146 95
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
(3)比较该市2016年6月与该市2015年全年的空气质量,2016年6月的空气质量是否好于去年?
跟踪训练一
1. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是________.(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
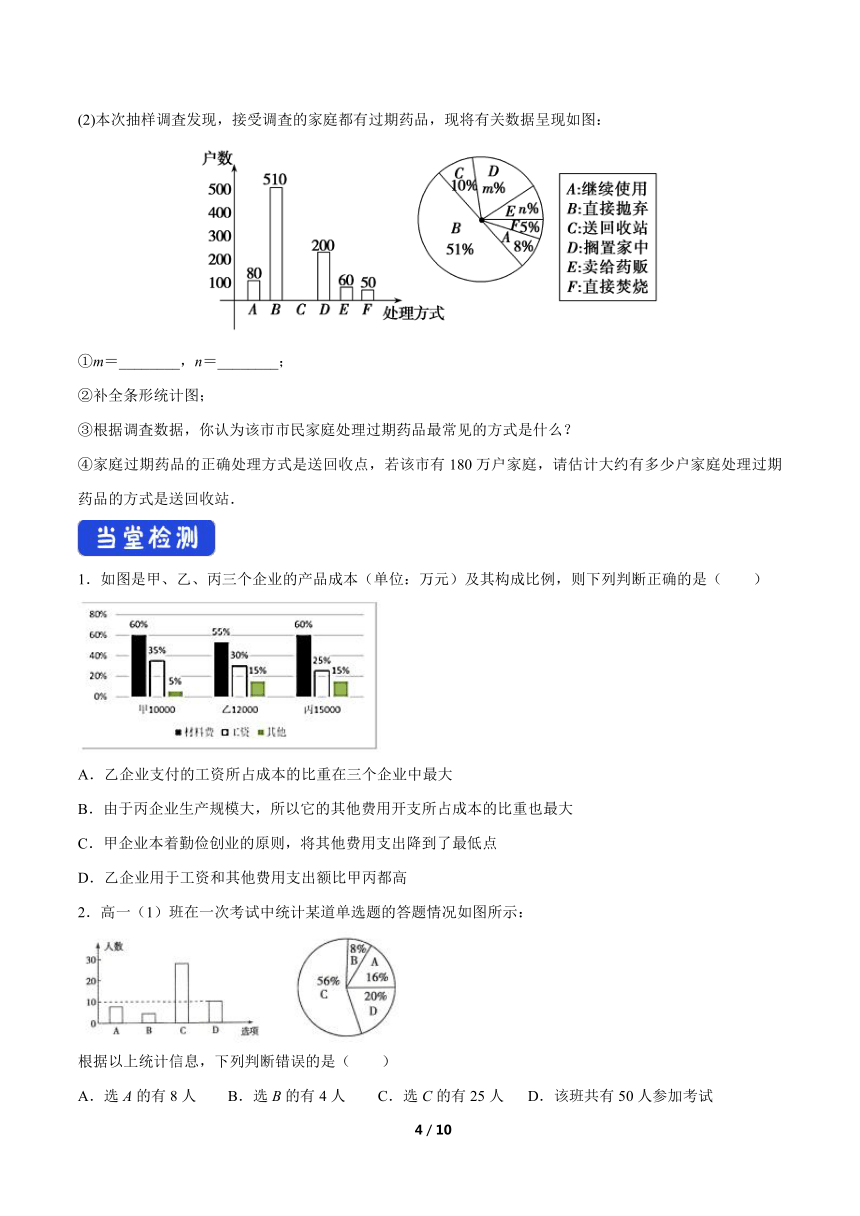
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
①m=________,n=________;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
1.如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )
A.乙企业支付的工资所占成本的比重在三个企业中最大
B.由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C.甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D.乙企业用于工资和其他费用支出额比甲丙都高
2.高一(1)班在一次考试中统计某道单选题的答题情况如图所示:
根据以上统计信息,下列判断错误的是( )
A.选A的有8人 B.选B的有4人 C.选C的有25人 D.该班共有50人参加考试
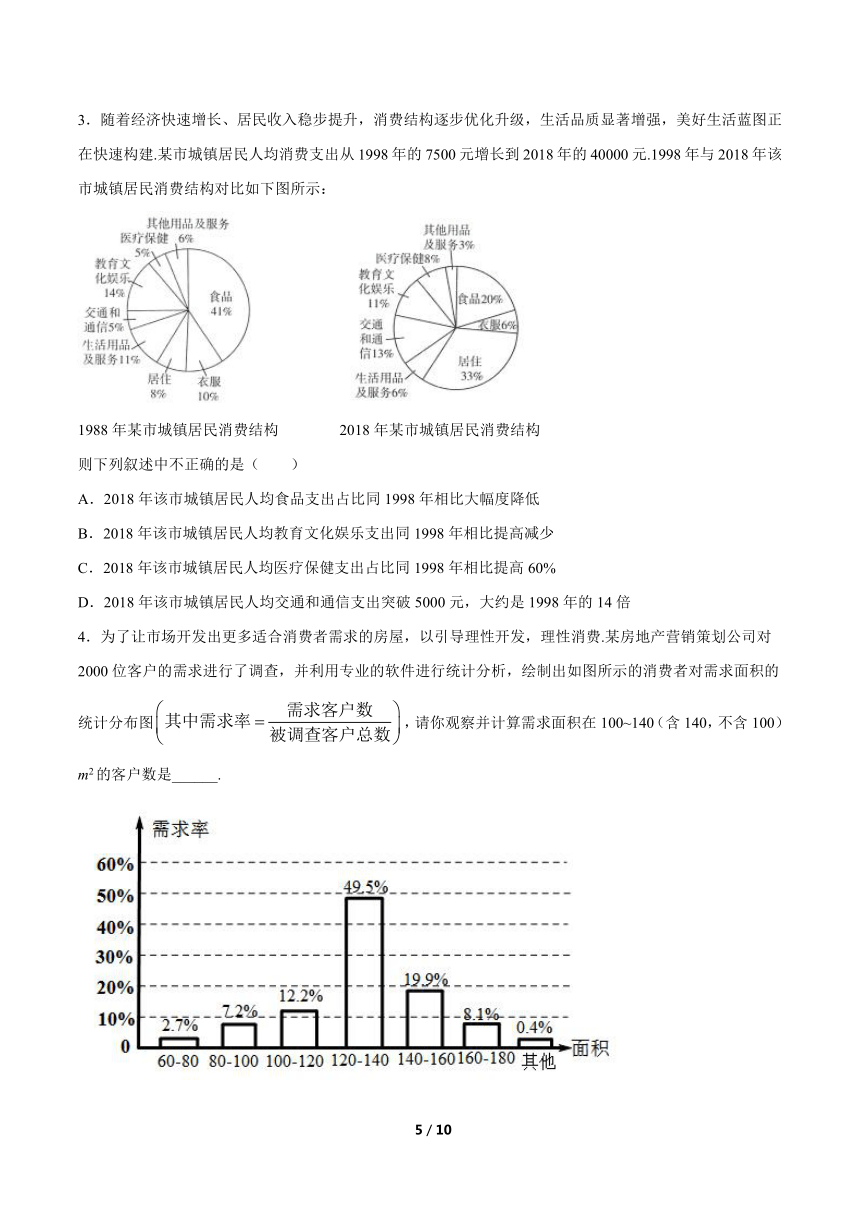
3.随着经济快速增长、居民收入稳步提升,消费结构逐步优化升级,生活品质显著增强,美好生活蓝图正在快速构建.某市城镇居民人均消费支出从1998年的7500元增长到2018年的40000元.1998年与2018年该市城镇居民消费结构对比如下图所示:
1988年某市城镇居民消费结构 2018年某市城镇居民消费结构
则下列叙述中不正确的是( )
A.2018年该市城镇居民人均食品支出占比同1998年相比大幅度降低
B.2018年该市城镇居民人均教育文化娱乐支出同1998年相比提高减少
C.2018年该市城镇居民人均医疗保健支出占比同1998年相比提高60%
D.2018年该市城镇居民人均交通和通信支出突破5000元,大约是1998年的14倍
4.为了让市场开发出更多适合消费者需求的房屋,以引导理性开发,理性消费.某房地产营销策划公司对2000位客户的需求进行了调查,并利用专业的软件进行统计分析,绘制出如图所示的消费者对需求面积的统计分布图,请你观察并计算需求面积在100~140(含140,不含100)m2的客户数是______.
5.某省有关部门要求各中小学要把“每天锻炼一小时”写入课程表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图(1)是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图(2)是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数为多少.
答案
小试牛刀
1.C.
2.C.
3.(1)三 (2)30%.
4. 4900.
自主探究
例1 【答案】见解析
【解析】(1)根据该市2016年6月的空气质量指数和空气质量等级分级标准,可以画出该市这个月的不同空气质量等级的频数与频率分布表(表2).
表2
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染
天数 4 15 9 2 0 0 30
比例 13.33% 50% 30% 6.67% 0 0 100%
从表中可以看出,“优”“良”的天数达19天,占了整月的63.33%,没有出现“重度污染”和“严重污染”.
我们可以用条形图和扇形图对数据作出直观的描述,如图1和图2.从条形图中可以看出,在前三个等级的占绝大多数,空气质量等级为“良”的天数最多,后三个等级的天数很少,从扇形图中可以看出,空气质量为“良”的天数占了总天数的一半,大约有三分之二为“优”“良”,大多数是“良”和“轻度污染”.因此,整体上6月的空气质量不错.
我们还可以用折线图展示空气质量指数随时间的变化情况,如图3.容易发现,6月的空气质量指数在100附近波动.
(2)根据该市2016年5月的空气质量指数和空气质量分级标准,可以画出该市这个月的不同空气质量等级的频数和频率分布表(表3).
表3
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染
天数 3 21 5 1 1 0 31
频率 10% 68% 16% 3% 3% 0 100%
为了便于比较,我们选用复合条形图,将两组数据同时反映到一个条形图上.通过条形图中柱的高低,可以更直观地进行两个月的空气质量的比较(下图).
由表3和图4可以发现,5月空气质量为“优”和“良”的总天数比6月多.所以,从整体上看,5月的空气质量略好于6月,但5月有重度污染,而6月没有.
(3)把2016年6月和2015年全年的空气质量进行比较,由于一个月和一年的天数差别很大,所以直接通过频数比较没有意义,应该转化成频率分布进行比较.可以通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较(图5).
通过图5可以看出,虽然2016年6月的空气质量为“优”的频率略低于2015年,但“良”的频率明显高于2015年,而且2016年6月中度以上的污染天气频率明显小于2015年.所以从整体上看,2016年6月的空气质量要好于2015年全年的空气质量.
跟踪训练一
1. 【答案】 (1)③ (2)①20 6 ②③④见解析
【解析】(1)根据抽样调查时选取的样本需具有代表性,可知下列选取样本的方法最合理的一种是③.
(2)①抽样调査的家庭总户数为:80÷8%=1 000(户),
m%=×100%=20%,m=20,
n%=×100%=6%,n=6.
②C类户数为:1 000-(80+510+200+60+50)=100,
条形统计图补充如下:
③根据调査数据,即可知道该市市民家庭处理过期药品最常见的方式是B类.
④180×10%=18(万户).
若该市有180万户家庭,估计大约有18万户家庭处理过期药品的方式是送回收站.
当堂检测
1-3. CCB
4. 1234.
5.【答案】(1)50名;(2)18人,36%;(3)160人.
【解析】(1)由题图(1)知:(名).
即该校对50名学生进行了抽样调查.
(2)本次调查中,最喜欢篮球活动的有18人,.
即最喜欢篮球活动的人数占被调查人数的36%.
(3),(人),(人),所以估计全校学生中最喜欢跳绳活动的人数为160人.
1 / 10
第2课时 统计图
1.理解频率分布表、折线图、条形图、扇形图的作用和识读.
2.了解不同的统计图在表示数据上有不同的特点.
1.直观想象:各种统计图的理解;
2.数学运算:各种统计图的相关计算.
重点:各种统计图的相关计算.
难点:各种统计图的理解.
预习导入
阅读课本198-200页,填写。
1.常见的其他统计图:条形图、扇形图、折线图.
扇形图主要用于直观描述各类数据占总数的比例;
条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率;
折线图主要用于描述数据随时间的变化趋势.
2.各个统计图特点
(1)不同的统计图在表示数据上有不同的特点.如扇形图主要用于直观描述各类数据占总数的 ,条形图和直方图主要用于直观描述不同类别或分组数据的 和 ,折线图主要用于描述数据随时间的变化趋势.
(2)不同的统计图适用的数据类型也不同.如条形图适用于描述 的数据,直方图适用于描述 数据.
1.要反映某市一周内每天的最高气温的变化情况,宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
2.调查机构对某高科技行业进行调查统计,得到该行业从业者学历分布扇形图、从事该行业岗位分布条形图,如图所示.
给出下列三种说法:①该高科技行业从业人员中学历为博士的占一半以上;②该高科技行业中从事技术岗位的人数超过总人数的30%;③该高科技行业中从事运营岗位的人员主要是本科生.其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
3.某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:
(1)该厂第一季度________月的产量最高.
(2)该厂一月份产量占第一季度总产量的________%.
4.该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%.请你估计:该厂第一季度大约生产了_______件合格的产品.
题型一 对折线图、扇形图、条形图的识读
例1 已知某市2015年全年空气质量等级如表1所示.
表1
空气质量等级(空气质量指数(AQI)) 频数 频率
优(AQI≤50) 83 22.8%
良(50
合计 365 100%
2016年5月和6月的空气质量指数如下:
5月 240 80 56 53 92 126 45 87 56 60
191 62 55 58 56 53 89 90 125 124
103 81 89 44 34 53 79 81 62 116
88
6月 63 92 110 122 102 116 81 163 158 76
33 102 65 53 38 55 52 76 99 127
120 80 108 33 35 73 82 90 146 95
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
(3)比较该市2016年6月与该市2015年全年的空气质量,2016年6月的空气质量是否好于去年?
跟踪训练一
1. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是________.(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
①m=________,n=________;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
1.如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )
A.乙企业支付的工资所占成本的比重在三个企业中最大
B.由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C.甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D.乙企业用于工资和其他费用支出额比甲丙都高
2.高一(1)班在一次考试中统计某道单选题的答题情况如图所示:
根据以上统计信息,下列判断错误的是( )
A.选A的有8人 B.选B的有4人 C.选C的有25人 D.该班共有50人参加考试
3.随着经济快速增长、居民收入稳步提升,消费结构逐步优化升级,生活品质显著增强,美好生活蓝图正在快速构建.某市城镇居民人均消费支出从1998年的7500元增长到2018年的40000元.1998年与2018年该市城镇居民消费结构对比如下图所示:
1988年某市城镇居民消费结构 2018年某市城镇居民消费结构
则下列叙述中不正确的是( )
A.2018年该市城镇居民人均食品支出占比同1998年相比大幅度降低
B.2018年该市城镇居民人均教育文化娱乐支出同1998年相比提高减少
C.2018年该市城镇居民人均医疗保健支出占比同1998年相比提高60%
D.2018年该市城镇居民人均交通和通信支出突破5000元,大约是1998年的14倍
4.为了让市场开发出更多适合消费者需求的房屋,以引导理性开发,理性消费.某房地产营销策划公司对2000位客户的需求进行了调查,并利用专业的软件进行统计分析,绘制出如图所示的消费者对需求面积的统计分布图,请你观察并计算需求面积在100~140(含140,不含100)m2的客户数是______.
5.某省有关部门要求各中小学要把“每天锻炼一小时”写入课程表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图(1)是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图(2)是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数为多少.
答案
小试牛刀
1.C.
2.C.
3.(1)三 (2)30%.
4. 4900.
自主探究
例1 【答案】见解析
【解析】(1)根据该市2016年6月的空气质量指数和空气质量等级分级标准,可以画出该市这个月的不同空气质量等级的频数与频率分布表(表2).
表2
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染
天数 4 15 9 2 0 0 30
比例 13.33% 50% 30% 6.67% 0 0 100%
从表中可以看出,“优”“良”的天数达19天,占了整月的63.33%,没有出现“重度污染”和“严重污染”.
我们可以用条形图和扇形图对数据作出直观的描述,如图1和图2.从条形图中可以看出,在前三个等级的占绝大多数,空气质量等级为“良”的天数最多,后三个等级的天数很少,从扇形图中可以看出,空气质量为“良”的天数占了总天数的一半,大约有三分之二为“优”“良”,大多数是“良”和“轻度污染”.因此,整体上6月的空气质量不错.
我们还可以用折线图展示空气质量指数随时间的变化情况,如图3.容易发现,6月的空气质量指数在100附近波动.
(2)根据该市2016年5月的空气质量指数和空气质量分级标准,可以画出该市这个月的不同空气质量等级的频数和频率分布表(表3).
表3
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染
天数 3 21 5 1 1 0 31
频率 10% 68% 16% 3% 3% 0 100%
为了便于比较,我们选用复合条形图,将两组数据同时反映到一个条形图上.通过条形图中柱的高低,可以更直观地进行两个月的空气质量的比较(下图).
由表3和图4可以发现,5月空气质量为“优”和“良”的总天数比6月多.所以,从整体上看,5月的空气质量略好于6月,但5月有重度污染,而6月没有.
(3)把2016年6月和2015年全年的空气质量进行比较,由于一个月和一年的天数差别很大,所以直接通过频数比较没有意义,应该转化成频率分布进行比较.可以通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较(图5).
通过图5可以看出,虽然2016年6月的空气质量为“优”的频率略低于2015年,但“良”的频率明显高于2015年,而且2016年6月中度以上的污染天气频率明显小于2015年.所以从整体上看,2016年6月的空气质量要好于2015年全年的空气质量.
跟踪训练一
1. 【答案】 (1)③ (2)①20 6 ②③④见解析
【解析】(1)根据抽样调查时选取的样本需具有代表性,可知下列选取样本的方法最合理的一种是③.
(2)①抽样调査的家庭总户数为:80÷8%=1 000(户),
m%=×100%=20%,m=20,
n%=×100%=6%,n=6.
②C类户数为:1 000-(80+510+200+60+50)=100,
条形统计图补充如下:
③根据调査数据,即可知道该市市民家庭处理过期药品最常见的方式是B类.
④180×10%=18(万户).
若该市有180万户家庭,估计大约有18万户家庭处理过期药品的方式是送回收站.
当堂检测
1-3. CCB
4. 1234.
5.【答案】(1)50名;(2)18人,36%;(3)160人.
【解析】(1)由题图(1)知:(名).
即该校对50名学生进行了抽样调查.
(2)本次调查中,最喜欢篮球活动的有18人,.
即最喜欢篮球活动的人数占被调查人数的36%.
(3),(人),(人),所以估计全校学生中最喜欢跳绳活动的人数为160人.
1 / 10
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
