人教A版(2019)高中数学必修第二册 9.2.1_总体取值规律的估计(第1课时)频率分布直方图_导学案
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 9.2.1_总体取值规律的估计(第1课时)频率分布直方图_导学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 624.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 11:23:28 | ||
图片预览



文档简介
9.2.1 总体取值规律的估计
第1课时 频率分布直方图
1.结合实例,能用样本估计总体的取值规律.
2.会列频率分布表,画频率分布直方图.
3.能根据频率分布表和频率分布直方图观测数据的分布规律.
1.直观想象:频率分布直方图的绘制与应用;
2.数学运算:频率分布直方图中的相关计算问题.
重点:①列频率分布表,画频率分布直方图;②根据频率分布表和频率分布直方图观测数据的分布规律.
难点:①列频率分布表,画频率分布直方图;②根据频率分布表和频率分布直方图观测数据的分布规律.
预习导入
阅读课本192-197页,填写。
1.频率分布直方图绘制步骤
①求 ,即一组数据中的最大值与最小值的差.
②决定 与 .组距与组数的确定没有固定的标准,一般数据的个数越多,所分组数越 .当样本容量不超过100时,常分成5~12组.为方便起见,一般取
组距,并且组距应力求“ ”.
③将数据 .
④列 表.计算各小组的频率,第i组的频率是 .
⑤画频率分布直方图.其中横轴表示分组,纵轴表示 . 实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的 程度.
2. 频率分布直方图意义:各个小长方形的面积表示相应各组的 ,频率分布直方图以 的形式反映数据落在各个小组的频率的大小,各小长方形的面积的总和等于 .
3.总体取值规律的估计:我们可以用样本观测数据的 估计总体的取值规律.
4.频率分布直方图的特征:当频率分布直方图的组数少、组距大时,容易从中看出数据整体的分布特点,但由于无法看出每组内的数据分布情况,损失了较多的 ;当频率分布直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得非常 ,不容易从中看出总体数据的分布特点.
1.判断下列说法是否正确.(正确的打“√”,错误的打“×”)
(1)一般样本容量越大,所分组数越多;样本容量越小,所分组数越小.( )
(2)频率分布直方图的横轴表示样本数据,纵轴表示频率.( )
(3)频率分布直方图中各个小长方形面积之和等于1.( )
2.关于频率分布直方图中的有关数据,下列说法正确的是( )
A.直方图的高表示该组上的个体在样本中出现的频率与组距的比值
B.直方图的高表示该组上的个体在样本中出现的频率
C.直方图的高表示取某数的频率
D.直方图的高表示该组上的个体数与组距的比值
3.一个容量为n的样本,分成若干组,已知某组的频数和频率分别为40,0.125,则n的值为( )
A.640 B.320
C.240 D.160
4.如图所示是一个容量为1 000的样本频率分布直方图,请根据图形中的数据填空.
(1)样本数据落在范围[5,9)的频率为________;
(2)样本数据落在范围[9,13)的频数为________.
题型一 频率分布直方图的绘制与应用
例1 一个农技站为了考察某种麦穗长的分布情况,在一块试验地里抽取了100个麦穗,量得长度如下(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6 5.8 5.5 6.0 6.5 5.1
6.5 5.3 5.9 5.5 5.8 6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4 6.8 6.0 6.3 5.5 5.0
6.3 5.2 6.0 7.0 6.4 6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0 5.8 5.3 7.0 6.0 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表、绘出频率分布直方图,并用自己的语言描述一下这批麦穗长的情况.
跟踪训练一
1. 某制造商3月份生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
分组 频数 频率
[39.95,39.97) 10
[39.97,39.99) 20
[39.99,40.01) 50
[40.01,40.03] 20
合计 100
补充完成频率分布表(结果保留两位小数),并在下图中画出频率分布直方图.
题型二 频率分布直方图中的相关计算问题
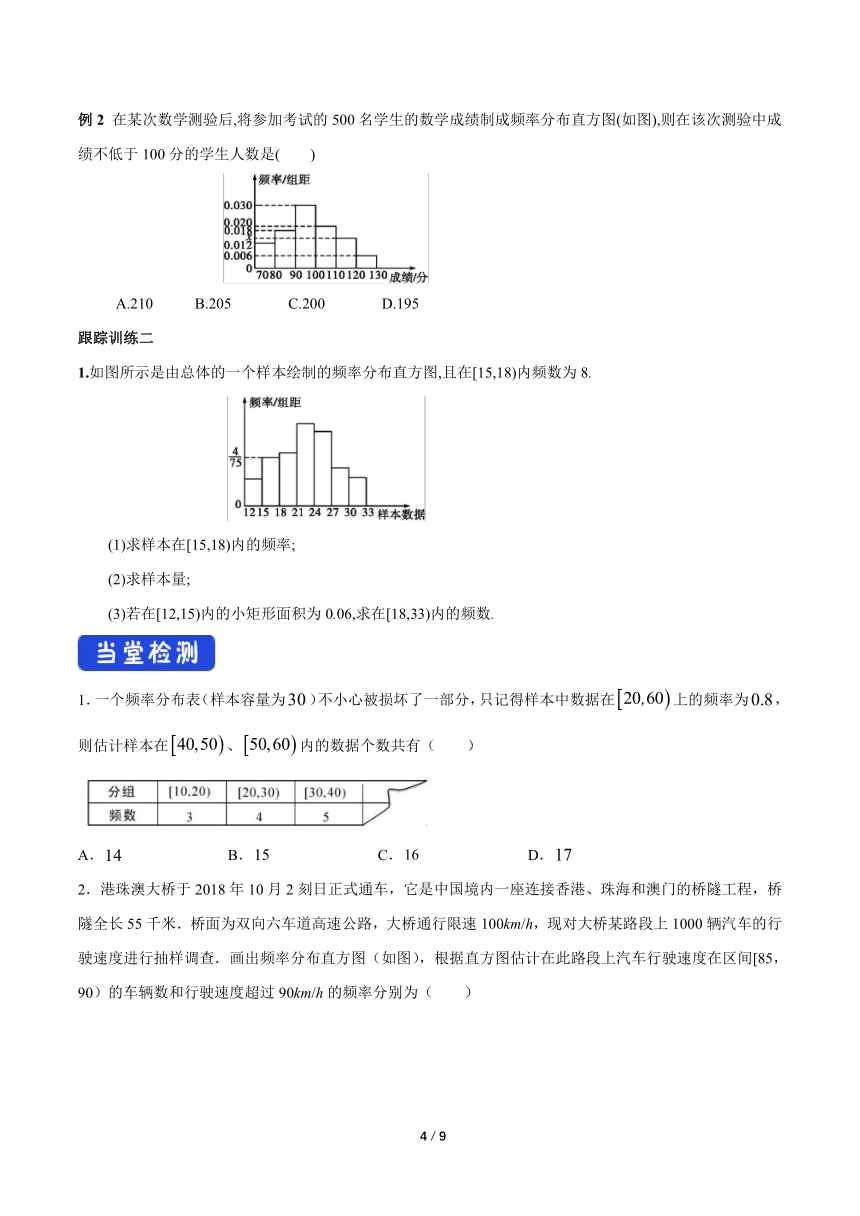
例2 在某次数学测验后,将参加考试的500名学生的数学成绩制成频率分布直方图(如图),则在该次测验中成绩不低于100分的学生人数是( )
A.210 B.205 C.200 D.195
跟踪训练二
1.如图所示是由总体的一个样本绘制的频率分布直方图,且在[15,18)内频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33)内的频数.
1.一个频率分布表(样本容量为)不小心被损坏了一部分,只记得样本中数据在上的频率为,则估计样本在、内的数据个数共有( )
A. B. C. D.
2.港珠澳大桥于2018年10月2刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米.桥面为双向六车道高速公路,大桥通行限速100km/h,现对大桥某路段上1000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h的频率分别为( )
A.300, B.300, C.60, D.60,
3.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组一次为若低于60分的人数是15人,则该班的学生人数是( )
A. B. C. D.
4.某重要路段限速70km/h,现对通过该路段的n辆汽车的车速进行检测,统计并绘成频率分布直方图(如图)若速度在60km/h~70km/h之间的车辆为150辆,则这n辆汽车中车速高于限速的汽车有_____辆.
5.某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机地抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
分组 频数 频率
① ②
0.050
0.200
36 0.300
0.275
12 ③
0.050
合计 ④
(1)根据上面的频率分布表,推出①②③④处的数字分别为 , , , .
(2)补全上的频率分布直方图.
(3)根据题中的信息估计总体:
①成绩在120分及以上的学生人数;
②成绩在的频率.
答案
小试牛刀
1. (1)√ (2)× (3)√.
2.A.
3.B.
4. (1)0.32 (2)360
自主探究
例1 【答案】见解析
【解析】步骤是:
(1)计算极差,7.4-4.0=3.4(cm).
(2)决定组距与组数.
若取组距为0.3 cm,由于=11,需分成12组,组数合适.于是取定组距为0.3 cm,组数为12.
(3)将数据分组.
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点.则所分的12个小组可以是[3.95,4.25),[4.25,4.55),[4.55,4.85),…,[7.25,7.55].
(4)列频率分布表.
对各个小组作频数累计,然后数频数,算频率,列频率分布表,如下表所示:
分组 频数累计 频数 频率
[3.95,4.25) 1 0.01
[4.25,4.55) 1 0.01
[4.55,4.85) 2 0.02
[4.85,5.15) 5 0.05
[5.15,5.45) 11 0.11
[5.45,5.75) 15 0.15
[5.75,6.05) 28 0.28
[6.05,6.35) 13 0.13
[6.35,6.65) 11 0.11
[6.65,6.95) 10 0.10
[6.95,7.25) 2 0.02
[7.25,7.55] 1 0.01
合计 100 1.00
(5)画频率分布直方图,如图.
从表中看到,从频率分布表中可以看出,绝大部分麦穗长集中在5.15-5.95,并且5.75-6.05占比最大.
跟踪训练一
1. 【答案】见解析.
【解析】频率分布表如下:
分组 频数 频率
[39.95,39.97) 10 0.10
[39.97,39.99) 20 0.20
[39.99,40.01) 50 0.50
[40.01,40.03] 20 0.20
合计 100 1.00
频率分布直方图如下:
例2 【答案】C
【解析】由频率分布直方图,得在该次测验中成绩不低于100分的学生的频率为1-(0.012+0.018+0.030)×10=0.4,
∴在该次测验中成绩不低于100分的学生人数为500×0.4=200.故选C.
跟踪训练二
1.【答案】(1). (2) 50. (3) 39.
【解析】 由样本频率分布直方图可知组距为3.
(1)由样本频率分布直方图得样本在[15,18)内的频率等于×3=.
(2)样本在[15,18)内的频数为8,由(1)可知,样本量为=8×=50.
(3)在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47.又因为在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.
当堂检测
1-3. BBB
4. 190.
5.【答案】(1)3; 0.025; 0.100; 1(2)见解析(3);
【解析】(1)在内的人数为36人,频率为0.300.
所以抽取的人数为人
在有12人,所以对应的频率为,故③对应的数字为0.100;
根据所有频率和为1,可知④对应的数字为1.则②对应的数字为 ,所以①对应的人数为
故①②③④处的数字分别为3; 0.025; 0.100; 1
(2)根据频率分布表,可得频率分布直方图如下图所示:
(3)①根据频率分布表及抽取总人数为120,可得成绩在120分及以上的学生人数为
人
②根据频率分布表,将内各组的频率求和可得
.
1 / 9
第1课时 频率分布直方图
1.结合实例,能用样本估计总体的取值规律.
2.会列频率分布表,画频率分布直方图.
3.能根据频率分布表和频率分布直方图观测数据的分布规律.
1.直观想象:频率分布直方图的绘制与应用;
2.数学运算:频率分布直方图中的相关计算问题.
重点:①列频率分布表,画频率分布直方图;②根据频率分布表和频率分布直方图观测数据的分布规律.
难点:①列频率分布表,画频率分布直方图;②根据频率分布表和频率分布直方图观测数据的分布规律.
预习导入
阅读课本192-197页,填写。
1.频率分布直方图绘制步骤
①求 ,即一组数据中的最大值与最小值的差.
②决定 与 .组距与组数的确定没有固定的标准,一般数据的个数越多,所分组数越 .当样本容量不超过100时,常分成5~12组.为方便起见,一般取
组距,并且组距应力求“ ”.
③将数据 .
④列 表.计算各小组的频率,第i组的频率是 .
⑤画频率分布直方图.其中横轴表示分组,纵轴表示 . 实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的 程度.
2. 频率分布直方图意义:各个小长方形的面积表示相应各组的 ,频率分布直方图以 的形式反映数据落在各个小组的频率的大小,各小长方形的面积的总和等于 .
3.总体取值规律的估计:我们可以用样本观测数据的 估计总体的取值规律.
4.频率分布直方图的特征:当频率分布直方图的组数少、组距大时,容易从中看出数据整体的分布特点,但由于无法看出每组内的数据分布情况,损失了较多的 ;当频率分布直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得非常 ,不容易从中看出总体数据的分布特点.
1.判断下列说法是否正确.(正确的打“√”,错误的打“×”)
(1)一般样本容量越大,所分组数越多;样本容量越小,所分组数越小.( )
(2)频率分布直方图的横轴表示样本数据,纵轴表示频率.( )
(3)频率分布直方图中各个小长方形面积之和等于1.( )
2.关于频率分布直方图中的有关数据,下列说法正确的是( )
A.直方图的高表示该组上的个体在样本中出现的频率与组距的比值
B.直方图的高表示该组上的个体在样本中出现的频率
C.直方图的高表示取某数的频率
D.直方图的高表示该组上的个体数与组距的比值
3.一个容量为n的样本,分成若干组,已知某组的频数和频率分别为40,0.125,则n的值为( )
A.640 B.320
C.240 D.160
4.如图所示是一个容量为1 000的样本频率分布直方图,请根据图形中的数据填空.
(1)样本数据落在范围[5,9)的频率为________;
(2)样本数据落在范围[9,13)的频数为________.
题型一 频率分布直方图的绘制与应用
例1 一个农技站为了考察某种麦穗长的分布情况,在一块试验地里抽取了100个麦穗,量得长度如下(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6 5.8 5.5 6.0 6.5 5.1
6.5 5.3 5.9 5.5 5.8 6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4 6.8 6.0 6.3 5.5 5.0
6.3 5.2 6.0 7.0 6.4 6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0 5.8 5.3 7.0 6.0 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表、绘出频率分布直方图,并用自己的语言描述一下这批麦穗长的情况.
跟踪训练一
1. 某制造商3月份生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
分组 频数 频率
[39.95,39.97) 10
[39.97,39.99) 20
[39.99,40.01) 50
[40.01,40.03] 20
合计 100
补充完成频率分布表(结果保留两位小数),并在下图中画出频率分布直方图.
题型二 频率分布直方图中的相关计算问题
例2 在某次数学测验后,将参加考试的500名学生的数学成绩制成频率分布直方图(如图),则在该次测验中成绩不低于100分的学生人数是( )
A.210 B.205 C.200 D.195
跟踪训练二
1.如图所示是由总体的一个样本绘制的频率分布直方图,且在[15,18)内频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33)内的频数.
1.一个频率分布表(样本容量为)不小心被损坏了一部分,只记得样本中数据在上的频率为,则估计样本在、内的数据个数共有( )
A. B. C. D.
2.港珠澳大桥于2018年10月2刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米.桥面为双向六车道高速公路,大桥通行限速100km/h,现对大桥某路段上1000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h的频率分别为( )
A.300, B.300, C.60, D.60,
3.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组一次为若低于60分的人数是15人,则该班的学生人数是( )
A. B. C. D.
4.某重要路段限速70km/h,现对通过该路段的n辆汽车的车速进行检测,统计并绘成频率分布直方图(如图)若速度在60km/h~70km/h之间的车辆为150辆,则这n辆汽车中车速高于限速的汽车有_____辆.
5.某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机地抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
分组 频数 频率
① ②
0.050
0.200
36 0.300
0.275
12 ③
0.050
合计 ④
(1)根据上面的频率分布表,推出①②③④处的数字分别为 , , , .
(2)补全上的频率分布直方图.
(3)根据题中的信息估计总体:
①成绩在120分及以上的学生人数;
②成绩在的频率.
答案
小试牛刀
1. (1)√ (2)× (3)√.
2.A.
3.B.
4. (1)0.32 (2)360
自主探究
例1 【答案】见解析
【解析】步骤是:
(1)计算极差,7.4-4.0=3.4(cm).
(2)决定组距与组数.
若取组距为0.3 cm,由于=11,需分成12组,组数合适.于是取定组距为0.3 cm,组数为12.
(3)将数据分组.
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点.则所分的12个小组可以是[3.95,4.25),[4.25,4.55),[4.55,4.85),…,[7.25,7.55].
(4)列频率分布表.
对各个小组作频数累计,然后数频数,算频率,列频率分布表,如下表所示:
分组 频数累计 频数 频率
[3.95,4.25) 1 0.01
[4.25,4.55) 1 0.01
[4.55,4.85) 2 0.02
[4.85,5.15) 5 0.05
[5.15,5.45) 11 0.11
[5.45,5.75) 15 0.15
[5.75,6.05) 28 0.28
[6.05,6.35) 13 0.13
[6.35,6.65) 11 0.11
[6.65,6.95) 10 0.10
[6.95,7.25) 2 0.02
[7.25,7.55] 1 0.01
合计 100 1.00
(5)画频率分布直方图,如图.
从表中看到,从频率分布表中可以看出,绝大部分麦穗长集中在5.15-5.95,并且5.75-6.05占比最大.
跟踪训练一
1. 【答案】见解析.
【解析】频率分布表如下:
分组 频数 频率
[39.95,39.97) 10 0.10
[39.97,39.99) 20 0.20
[39.99,40.01) 50 0.50
[40.01,40.03] 20 0.20
合计 100 1.00
频率分布直方图如下:
例2 【答案】C
【解析】由频率分布直方图,得在该次测验中成绩不低于100分的学生的频率为1-(0.012+0.018+0.030)×10=0.4,
∴在该次测验中成绩不低于100分的学生人数为500×0.4=200.故选C.
跟踪训练二
1.【答案】(1). (2) 50. (3) 39.
【解析】 由样本频率分布直方图可知组距为3.
(1)由样本频率分布直方图得样本在[15,18)内的频率等于×3=.
(2)样本在[15,18)内的频数为8,由(1)可知,样本量为=8×=50.
(3)在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47.又因为在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.
当堂检测
1-3. BBB
4. 190.
5.【答案】(1)3; 0.025; 0.100; 1(2)见解析(3);
【解析】(1)在内的人数为36人,频率为0.300.
所以抽取的人数为人
在有12人,所以对应的频率为,故③对应的数字为0.100;
根据所有频率和为1,可知④对应的数字为1.则②对应的数字为 ,所以①对应的人数为
故①②③④处的数字分别为3; 0.025; 0.100; 1
(2)根据频率分布表,可得频率分布直方图如下图所示:
(3)①根据频率分布表及抽取总人数为120,可得成绩在120分及以上的学生人数为
人
②根据频率分布表,将内各组的频率求和可得
.
1 / 9
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
