2022-2023学年上学期京改版数学七年级上册(北京地区)第二章 一元一次方程 期末综合复习题(含解析)
文档属性
| 名称 | 2022-2023学年上学期京改版数学七年级上册(北京地区)第二章 一元一次方程 期末综合复习题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 473.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 14:16:14 | ||
图片预览




文档简介
第二章 一元一次方程 期末综合复习题
一、单选题
1.(2022·北京市通州区北关中学七年级期中)用代数式表示的倍的平方与的差正确的是( )
A. B. C. D.
2.(2022·北京市第十二中学七年级期中)若与是同类项,则|m﹣n|的值是( )
A.0 B.1 C.7 D.﹣1
3.(2022·北京育才学校七年级期中)下列运算中,正确的是( )
A.5m2﹣4m2=1 B.3a2b﹣3ba2=0
C.3a+2b=5ab D.2x3+3x2=5x5
4.(2022·北京市第十二中学七年级期中)已知x=2是方程3x﹣5=2x+m的解,则m的值是( )
A.1 B.﹣1 C.3 D.﹣3
5.(2022·北京十五中七年级期中)下列运用等式性质进行的变形,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.(2022·北京市第十二中学七年级期中)下列方程中,一元一次方程共有( )个
①;②;③; ④;⑤;⑥
A.1个 B.2个 C.3个 D.4个
7.(2022·北京师大附中七年级期中)方程3x+6=0与关于x的方程3x=2﹣2m的解相同,则m的值为( )
A.﹣2 B.2 C.3 D.4
8.(2022·北京市第一六一中学七年级期中)如果代数式与的值互为相反数,则的值为( )
A. B. C. D.
9.(2022·北京十四中七年级期中)如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示).请你运用所学的数学知识来研究,则这7个数的和不可能是( )
A.63 B.70 C.105 D.96
10.(2022·北京市怀柔区桥梓中学七年级阶段练习)有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车,若每辆客车乘43 人, 则只有 1人不能上车,有下列四个等式:
①,②,
③,④,
其中符合题意的是 ( )
A.①②③ B.②③④ C.③④ D.②③
二、填空题
11.(2022·北京海淀·七年级期中)一种商品每件成本为a元,按成本增加25%定价,售出60件,可盈利___________元(用含a的式子表示).
12.(2022·北京市通州区北关中学七年级期中)单项式与是同类项,则___________
13.(2022·北京市第十三中学分校七年级期中)若2是关于的一元一次方程的解,则___________.
14.(2022·北京市第十二中学七年级期中)若 是关于x的一元一次方程,则 ________.
15.(2022·北京二中七年级期中)对于两个不相等的有理数a,b,我们规定符号表示a,b两数中较大的数,例如.按照这个规定,方程的解为_______.
16.(2022·北京市平谷区峪口中学七年级阶段练习)双层游轮的票价是上层票每张12元,下层票每张8元,现在游轮上共有游客150人,而且下层票的总票款比上层票的总票款多700元.那么这艘轮船上下两层游客的人数分别是多少 设这艘邮轮上层的游客人,这艘油轮下层的游客人,可列方程组为__________.
三、解答题
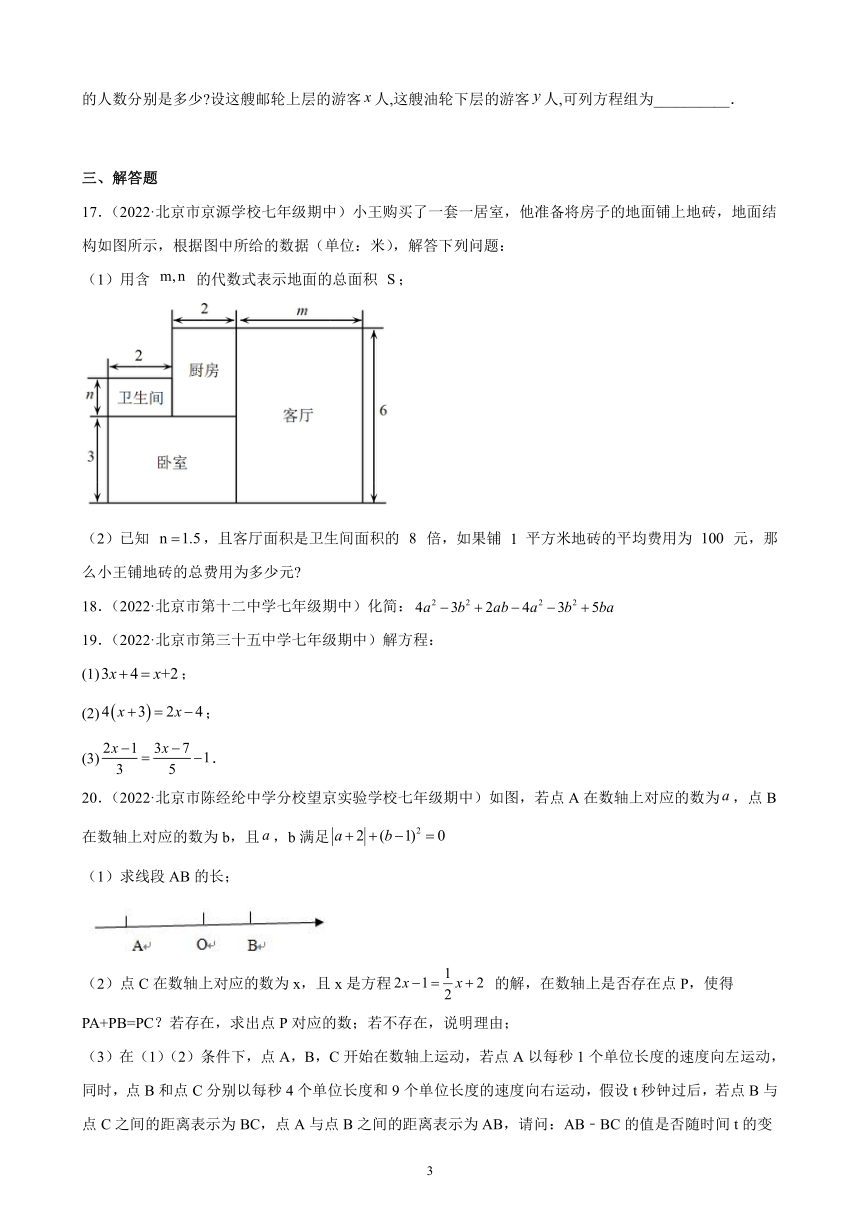
17.(2022·北京市京源学校七年级期中)小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含 的代数式表示地面的总面积 ;
(2)已知 ,且客厅面积是卫生间面积的 倍,如果铺 平方米地砖的平均费用为 元,那么小王铺地砖的总费用为多少元
18.(2022·北京市第十二中学七年级期中)化简:
19.(2022·北京市第三十五中学七年级期中)解方程:
(1);
(2);
(3).
20.(2022·北京市陈经纶中学分校望京实验学校七年级期中)如图,若点A在数轴上对应的数为,点B在数轴上对应的数为b,且,b满足
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
21.(2022·北京市第三十五中学七年级期中)列方程组解应用题
某地需要将一段长为180米的河道进行整修,整修任务由A,B两个工程队先、后接力完成.已知A工程队每天整修12米,B工程队每天整修8米,共用时20天.问A,B两个工程队整修河道分别工作了多少天?
22.(2022·北京师范大学亚太实验学校七年级期中)列方程(组)解决下列问题
某蔬菜公司收购到一批蔬菜,计划用天加工后上市销售,该公司的加工能力是:每天可以精加工吨或者粗加工吨,且每吨蔬菜精加工后的利润为元,粗加工后的利润为元,已知公司售完这批加工后的蔬菜,共获得利润元,求这批蔬菜共多少吨?
23.(2022·北京顺义·七年级期末)某校组织学生参加冬奥会知识竞赛,共设20道单项选择题,各题分值相同,每题必答,下表是部分参赛者的得分统计表:
参赛者 答对题数 答错题数 得分
于潇 20 0 100
王晓林 18 2 88
李毅 10 10 40
… … … …
(1)根据表格提供的数据,答对1题得_______分,答错1题扣________分;
(2)参赛者李小萌得了76分,求她答对了几道题.
24.(2022·北京市陈经纶中学分校七年级期中)某区运动会要印刷秩序册,有两个印刷厂前来联系业务,他们的报价相同,甲厂的优惠条件是:按每份定价6元的八折收费,另收500元制版费;乙厂的优惠条件是:每份定价6元的价格不变,而500元的制版费四折优惠.
问:(1)这个区印制多少份秩序册时两个印刷厂费用是相同的;
(2)当印制200份、400份秩序册时,选哪个印刷厂所付费用较少;为什么.
25.(2022·北京市京源学校七年级期中)将连续的偶数2,4,6,8,…排成如下表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和等于 .
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为x,用代数式表示十字框中的五个数的和是 .
(3)在移动十字框的过程中,若框住的五个数的和等于2020,这五个数从小到大依次 , , , , .
(4)框住的五个数的和能等于2019吗?
26.(2022·北京市第一六一中学七年级期中)如图,在数轴上有A,B两点,且AB=8,点A表示的数为6;动点P从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
(1)写出数轴上点B表示的数是 ;
(2)当t=2时,线段PQ的长是 ;
(3)当0<t<3时,则线段AP= ;(用含t的式子表示)
(4)当PQ=AB时,求t的值.
27.(2022·北京朝阳·七年级期中)如图,在数轴上点A、C、B表示的数分别是-2、1、12.动点P从点A出发,沿数轴以每秒3个单位长度的速度向终点B匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向终点A匀速运动,设点Q的运动时间为t秒.
(1)AB的长为_______;
(2)当点P与点Q相遇时,求t的值.
(3)当点P与点Q之间的距离为9个单位长度时,求t的值.
(4)若PC+QB=8,直接写出t点P表示的数.
28.(2022·北京昌平·七年级期中)【概念学习】
点A,B,C为数轴上的三点,如果点C到A的距离是点C到B的距离的2倍,那么我们就称点C是的偶点.
如图1,点A表示的数为,点B表示的数为1,表示0的点C到点A的距离是2,到点B的距离是1,那么点C是的偶点;表示的点D到点A的距离是1,到点B的距离是2,那么点D就不是的偶点,但点D是的偶点.
【初步探究】
已知如图2,M,N为数轴上两点,点M表示的数为,点N表示的数为5,若点F是的偶点,回答下列问题:
(1)当F在点M,N之间,点F表示的数为__________;
(2)当F为数轴上一点,点F表示的数为____________;
【深入思考】
(3)如图3,P、Q为数轴上两点,点P表示的数为,点Q表示的数为40,现有一个动点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,求当t为何值时,P,Q,E中恰有一个点为其余两点的偶点?
29.(2022·北京市怀柔区桥梓中学七年级阶段练习)把450棵树苗分给一中队、二中队,使两个中队分得的树苗的比是4:5,每个中队各分到树苗多少棵?
参考答案:
1.A
【解析】根据题意可直接列出代数式即可.
解:由题意得:;
故选A.
【点睛】本题主要考查列代数式,读懂题意是解题的关键.
2.B
【解析】直接利用同类项的概念得出n,m的值,再利用绝对值的性质求出答案.
解:∵与是同类项,
∴2m=1,2n=3,
解得:m=,n=,
∴|m﹣n|=|﹣|=1.
故选:B.
【点睛】此题主要考查了同类项,正确把握同类项的定义是解题关键.
3.B
【解析】根据合并同类项法则即可依次判断.
A、5m2﹣4m2=m2,故本选项不合题意;
B、3a2b﹣3ba2=0,故本选项符合题意;
C、3a与2b不是同类项,所以不能合并,故本选项不合题意;
D、2x3与3x2不是同类项,所以不能合并,故本选项不合题意;
故选:B.
【点睛】此题主要考查整式的加减,解题的关键是熟知合并同类项法则.
4.D
【解析】把x=2代入方程3x﹣5=2x+m可得到关于m的方程,解方程可求得m的值.
解:∵x=2是方程3x﹣5=2x+m的解,
∴把x=2代入方程可得6﹣5=4+m,
解得m=﹣3,
故选:D.
【点睛】本题主要考查一元一次方程的解的定义,掌握能使方程左右两边同时成立的未知数的值是方程的解是解题的关键.
5.B
【解析】根据等式的性质判断即可.
解:A、若,当时,两边都除以c无意义,故此选项不符合题意;
B、若,两边都乘以c,得,故此选项符合题意;
C、若,得或,故此选项不符合题意;
D、若,两边都乘以,得,故此选项不符合题意.
故选:B.
【点睛】本题考查等式的基本性质,解决本题的关键是掌握等式的两边同时加上(或减去)同一个数(或式子),等式仍成立;等式的两边同时乘以(或除以)同一个不为零的数(或式子),等式仍成立.
6.C
【解析】根据一元一次方程的定义进行解答即可.
解:①,是一元一次方程,符合题意;
②,含有2个未知数,不是一元一次方程,不合题意;
③,分母含有字母,不是一元一次方程,不合题意;
④,是一元一次方程,符合题意;
⑤,未知数的最高次数是2,不是一元一次方程,不合题意;
⑥,是一元一次方程,符合题意.
综合上分析可得,是一元一次方程的是:①④⑥,
故选:C.
【点睛】本题考查了一元一次方程的定义,只含有一个未知数(元),未知数的次数都是1,等号两边都是整式,这样的方程叫作一元一次方程,能熟记一元一次方程的定义是解此题的关键.
7.D
【解析】先求解关于x的一元一次方程,然后代入求解即可.
解:3x+6=0,
解得:x=-2,
将x=-2代入3x=2-2m中,得,
-6=2-2m,
解得:m=4,
故选:D.
【点睛】题目主要考查解一元一次方程及一元一次方程的解,熟练掌握解一元一次方程是解题关键.
8.D
【解析】利用互为相反数之和为0列出方程,求出方程的解即可得到的值.
解:根据题意,得,
解得:,
故选D.
【点睛】本题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把系数化为1,即可求出解.
9.D
【解析】设“H”型框中的正中间的数为,则其他6个数分别为,,,,,,表示出这7个数之和,然后分别列出方程解答即可.
解:设“H”型框中的正中间的数为x,则其他6个数分别为,,,,,,这7个数之和为: .
由题意得
A.,解得:,能求得这7个数;
B. ,解得:,能求得这7个数;
C.,解得:,能求得这7个数;
D.,解得: ,此时不能求得这7个数.
故选:D.
【点睛】此题考查一元一次方程的实际运用,掌握“H”型框中的7个数的数字的排列规律是解决问题的关键.
10.C
【解析】首先要理解清楚题意,知道总的客车数量及总的人数不变,然后采用排除法进行分析从而得到正确答案.
解:根据总人数列方程,应是,
则④正确,①错误,
根据客车数列方程,应该为,
则③正确,②错误,
则正确的是③,④,
故选C.
【点睛】此题考查了由实际问题抽象出一元一次方程的知识,解题的关键是能够根据不同的等量关系列方程.
11.
【解析】根据利润=售价-进价列出代数式即可.
解:一种商品每件成本为a元,按成本增加25%定价,售出60件,可盈利(元).
故答案为:.
【点睛】本题主要考查了列代数式,解题的关键是熟练掌握利润=售价-进价.
12.
【解析】根据单项式的定义,字母相同且对应字母的指数相同求得的值,进而合并同类项即可求解.
解:∵单项式与是同类项,
∴,
解得
∴
故答案为:
【点睛】本题考查了同类项的定义,合并同类项,掌握同类项的定义求得的值是解题的关键.
13.
【解析】把x=2代入方程即可得到一个关于a的方程,解方程即可求解.
解:把x=2代入方程得,
解得a=.
故答案是:.
【点睛】本题考查了方程的解的定义,解一元一次方程,就是能够使方程左右两边相等的未知数的值.
14.1
【解析】把只含有一个未知数,并且未知数的次数是1的整式方程称为一元一次方程,根据一元一次方程的概念即可完成解答.
由题意得:3-2a=1,
解得:a=1,
故答案为:1.
【点睛】本题考查了一元一次方程的概念,把握一元一次方程的概念要注意三点:①只含一个未知数,即一元;②未知数的次数是1,即一次;③方程两边都是整式.
15.
【解析】根据题意可排除x为非负数的情形,则考虑x正数的情形,然后解一元一次方程即可.
当x为正数时,则,
即x不可能为正数,故x为负数,
所以,
解得;
故答案为:.
【点睛】本题考查了解一元一次方程,关键是弄懂符号的含义,另外要考虑x的取值情况.
16.
【解析】设这艘游轮上层的游客人数为x人,下层的游客人数为y人,根据“游轮上共有游客150人,而且下层票的总票款是上层票的总票款多700元”列方程组求解可得.
这艘邮轮上层的游客人,这艘油轮下层的游客人,由题意得
.
故答案为.
【点睛】本题主要考查二元一次方程组的应用,理解题意找出题目中所蕴含的等量关系是列出方程组求解的关键.
17.(1)S=6m+2n+18;(2) 铺地砖的总费用4500元
【解析】(1)根据总面积等于四个部分矩形的面积之和列式整理即可得解;
(2)根据题意求出m的值,把m,n的值代入计算即可.
(1)S=2n+6m+3×4+2×3=6m+2n+18.
(2)n=1.5时2n=3
根据题意,得6m=8×3=24,
∵铺1平方米地砖的平均费用为100元,
∴铺地砖的总费用为:
100(6m+2n+18)=100×(24+3+18)=4500.
答:铺地砖的总费用4500元.
【点睛】此题考查了列代数式,准确表示出各部分矩形的长和宽是解题的关键.
18.
【解析】先确定多项式中的同类项,再合并同类项即可.
解:原式
.
【点睛】本题考查的是合并同类项,掌握“同类项的含义与合并同类项的法则”是解本题的关键.
19.(1)
(2)
(3)
【解析】(1)移项,解方程即可.
(2)先去括号,后依次求解即可.
(3)先去分母,再去括号,后依次求解即可.
(1)解:,
移项,得
,
合并同类项,得
,
系数化为1,得
.
(2)解:
去括号,得
移项,得
,
合并同类项,得
,
系数化为1,得
.
(3)解:,
去分母,得
去括号,得
移项,得
,
合并同类项,得
.
【点睛】本题考查了一元一次方程的解法,熟练掌握解方程的基本步骤是解题的关键.
20.(1)AB=3.
(2)P所对应的数是﹣3或﹣1.
(3)不随t的变化而变化,其常数值为2.
试题分析:(1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数;
(3)用含有t的代数式表示出AB和BC,求差即可.
试题解析:(1)∵|a+2|+(b﹣1)2=0,
∴a=﹣2,b=1,
∴AB=b﹣a=1﹣(﹣2)=3.
(2)2x﹣1=x+2,
解得:x=2,
由题意得,点P只能在点B的左边,
①当点P在AB之间时,x+2+1﹣x=2﹣x,
解得:x=﹣1;
②当点P在A点左边时,﹣2﹣x+1﹣x=2﹣x,
解得:x=﹣3,
综上可得P所对应的数是﹣3或﹣1.
(3)t秒钟后,A点位置为:﹣2﹣t,B点的位置为:1+4t, C点的位置为:2+9t
BC=2+9t﹣(1+4t)=1+5t AB=5t+3
AB﹣BC=5t+3﹣(5t+1)=2
所以不随t的变化而变化,其常数值为2.
考点:一元一次方程的应用.
21.A工程队整修河道工作了5天,则B工程队整修河道工作了15天.
【解析】设A工程队整修河道工作了x天,则B工程队整修河道工作了(20-x)天,根据题意,列出方程,即可求解.
解:设A工程队整修河道工作了x天,则B工程队整修河道工作了(20-x)天,根据题意得:
,
解得:,
∴20-x=15,
答:A工程队整修河道工作了5天,则B工程队整修河道工作了15天.
【点睛】本题主要考查了一元一次方程的应用,明确题意,准确得到等量关系是解题的关键.
22.吨
【解析】设精加工天,则粗加工天,利用总利润精加工的天数粗加工的天数,即可得出关于的一元一次方程,解之即可得出的值,再将其代入中即可求出结论.
解:设精加工天,则粗加工天,
依题意得:,
解得:,
.
答:这批蔬菜共吨.
【点睛】本题考查一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
23.(1)答对1题得5分,答错1题扣1分;
(2)她答对16道题.
【解析】(1)先根据于潇的得分可得出答对1题得5分,再根据王晓林的得分即可得出答错1题扣的分数;
(2)设参赛者李小萌答对了道题,从而可得她答错了道题,根据(1)的结果和“参赛者李小萌得了76分”建立方程,解方程即可得.
(1)
解:答对1题得的分数为(分),
答错1题扣的分数为(分),
故答案为:5,1;
(2)
解:设参赛者李小萌答对了道题,则她答错了道题,
由题意得:,
解得,
答:她答对了16道题.
【点睛】本题考查了有理数加减乘除的应用、一元一次方程的应用,正确建立方程是解题关键.
24.(1)250份;(2)当印制200份秩序册时,选乙印刷厂所付费用较少;当印制400份秩序册时选甲印刷厂所付费用较少,理由见解析.
【解析】(1)设要印制x份节目单,则甲厂的收费为500+6×0.8x元,乙厂的收费为6x+500×0.4元,根据费用相同列方程即可解答;
(2)把x=200分别代入甲厂费用500+6×0.8x和乙厂费用6x+500×0.4,比较得出答案. 同样再把x=400分别代入计算比较.
解:(1)设这个区要印制x份秩序册时费用是相同的,根据题意得,
500+6×0.8x=6x+500×0.4,
解得x=250,
答:要印制250份秩序册时费用是相同的.
(2)当印制200份秩序册时:
甲厂费用需:0.8×6×200+500=1460(元),
乙厂费用需:6×200+500×0.4=1400(元),
因为1400<1460,
故选乙印刷厂所付费用较少.
当印制400份秩序册时:
甲厂费用需:0.8×6×400+500=2420(元),
乙厂费用需:6×400+500×0.4=2600(元),
因为2420<2600,
故选甲印刷厂所付费用较少.
【点睛】本题考查了列一元一次方程解决实际问题,一般步骤是: ①审题,找出已知量和未知量;②设未知数,并用含未知数的代数式表示其它未知量;③找等量关系,列方程;④解方程;⑤检验方程的解是否符合题意并写出答案.
25.(1)80;(2)5x;(3)这五个数分别为:394,402,404,406,414;(4)不能
【解析】(1)根据有理数的加法法则计算;
(2)根据图中数字的规律分别表示另外四个数,列式计算即可;
(3)根据(2)列方程5x=2020,求解即可;
(4)列方程5x=2019,求解判断即可.
解:(1)6+14+16+18+26=80,
故答案为:80;
(2)设中间的数为x,则其他四个数分别为x-10,x-2,x+2,x+10,
∴这五个数的和是x-10+x-2+x+x+2+x+10=5x,
故答案为:5x;
(3)由(2)得,设中间的数为x,则这五个数的和是5x,
∴5x=2020,
解得x=404,
∴这五个数分别为:394,402,404,406,414;
故答案为:394,402,404,406,414;
(4)由(2)得,设中间的数为x,则这五个数的和是5x,
∴5x=2019,
解得,
∵x是整数且为偶数,
∴框住的五个数的和不能等于2019.
【点睛】此题考查有理数的加法法则,列代数式的实际应用,解一元一次方程,熟练掌握各知识点并应用解决问题是解题的关键.
26.(1)14;(2)4;(3)6﹣2t;(4)t的值是4或8
【解析】(1)根据两点间的距离公式即可求出数轴上点B表示的数;
(2)先求出当t=2时,P点对应的有理数为2×2=4,Q点对应的有理数为6+1×2=8,再根据两点间的距离公式即可求出PQ的长;
(3)先求出当0<t<3时,P点对应的有理数为2t<6,再根据两点间的距离公式即可求出AP的长;
(4)由于t秒时,P点对应的有理数为2t,Q点对应的有理数为6+t,根据两点间的距离公式得出PQ=|2t﹣(6+t)|=|t﹣6|,根据PQAB列出方程,解方程即可求解.
(1)6+8=14.
故数轴上点B表示的数是14;
(2)当t=2时,P点对应的有理数为2×2=4,Q点对应的有理数为6+1×2=8,
8﹣4=4.
故线段PQ的长是4;
(3)当0<t<3时,P点对应的有理数为2t<6,
故AP=6﹣2t;
(4)根据题意可得:
|t﹣6|8,
解得:t=4或t=8.
故t的值是4或8.
【点睛】本题考查了一元一次方程的应用和数轴,解答本题的关键是掌握点的移动与点所表示的数之间的关系,(4)中解方程时要注意分两种情况进行讨论.
27.(1)14
(2)当t为秒时,点P与点Q相遇;
(3)当t为1秒或秒时,点P与点Q间的距离为9个单位长度;
(4)存在某一时刻使得PC+QB=8,此时点P表示的数为.
【解析】(1)根据两点之间的距离公式直接求出AB的长;
(2)当运动时间为t秒时,点P表示的数为3t-2,点Q表示的数为-2t+12;由点P,Q相遇,即可得出关于t的一元一次方程,解之即可得出结论;
(3)由PQ=9,即可得出关于t的一元一次方程,解之即可得出结论;
(4)当运动时间为t秒时,点P表示的数为3t-2,PC=|3t-2-1|=|3t-3|,QB=2t,由PC+QB=8,即可得出关于t的一元一次方程,解之即可得出t的值,再将其代入3t-2中即可求出结论.
(1)
解:AB=12-(-2)=14,
故答案为:14;
(2)
解:当运动时间为t秒时,点P表示的数为3t-2,点Q表示的数为-2t+12.
依题意得:3t-2=-2t+12,
解得:t=.
答:当t为秒时,点P与点Q相遇;
(3)
解:依题意得:-2t+12-(3t-2)=9或3t-2-(-2t+12)=9,
解得:t=1或t=.
答:当t为1秒或秒时,点P与点Q间的距离为9个单位长度;
(4)
解:当运动时间为t秒时,点P表示的数为3t-2,PC=|3t-2-1|=|3t-3|,QB=2t.
依题意得:|3t-3|+2t=8,
即3-3t+2t=8或3t-3+2t=8,
解得:t=-5(不合题意,舍去)或t=,
∴3t-2=.
答:存在某一时刻使得PC+QB=8,此时点P表示的数为.
【点睛】本题考查了一元一次方程的应用以及数轴,解题的关键是:(1)利用数轴上两点间的距离,找出点B,C表示的数;(2)找准等量关系,正确列出一元一次方程;(3)找准等量关系,正确列出一元一次方程;(4)找准等量关系,正确列出一元一次方程.
28.(1)3;
(2)3或11;
(3)10秒、15秒或20秒.
【解析】(1)根据偶点的定义,列方程求解即可;
(2)根据题意,分两种情况,分别列方程求解即可;
(3)根据题意,分四种情况分类讨论:①当点E是的偶点时,;②当点E是的偶点时,;③当点Q是的偶点时,;④点P是的偶点时,;然后分别列方程求解得解.
(1)解: 设点F表示的数是x,
点F是的偶点,F在点M,N之间,
即,
即点F表示的数是3;
故答案为:3.
(2)解:设点F表示的数是x,依题,得
或
解得:或11;
故答案为:3或11.
(3)解:点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,则动点E的表示的数为, ,.
分四种情况讨论:
①当点E是的偶点时,,
,
解得:(秒);
②当点E是的偶点时,,
,
解得:(秒);
③当点Q是的偶点时,,
,
解得:(秒);
④点P是的偶点时,,
,
解得:(秒)
综上所述,当为10秒、15秒或20秒时,E、P、Q中恰有一个点为其余两点的偶点.
【点睛】此题考查了数轴上的动点问题与一元一次方程的应用,准确读懂题意、理解偶点的定义、找出正确的等量关系是解此题的关键.
29.一中队、二中队分到树苗200棵、250棵.
【解析】根据总量是450棵树苗,是按照两个中队分得树苗的比为4:5进行分配的,先求出两个中队分得树苗的总份数,进一步求出一份树苗数的数量,最后分别求得每个中队分到树苗的棵数.
解:450÷(4+5)=50
一中队:4×50=200棵
二中队:5×50=250棵
答:一中队、二中队分到树苗200棵、250棵.
考点:比例的应用题.
一、单选题
1.(2022·北京市通州区北关中学七年级期中)用代数式表示的倍的平方与的差正确的是( )
A. B. C. D.
2.(2022·北京市第十二中学七年级期中)若与是同类项,则|m﹣n|的值是( )
A.0 B.1 C.7 D.﹣1
3.(2022·北京育才学校七年级期中)下列运算中,正确的是( )
A.5m2﹣4m2=1 B.3a2b﹣3ba2=0
C.3a+2b=5ab D.2x3+3x2=5x5
4.(2022·北京市第十二中学七年级期中)已知x=2是方程3x﹣5=2x+m的解,则m的值是( )
A.1 B.﹣1 C.3 D.﹣3
5.(2022·北京十五中七年级期中)下列运用等式性质进行的变形,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.(2022·北京市第十二中学七年级期中)下列方程中,一元一次方程共有( )个
①;②;③; ④;⑤;⑥
A.1个 B.2个 C.3个 D.4个
7.(2022·北京师大附中七年级期中)方程3x+6=0与关于x的方程3x=2﹣2m的解相同,则m的值为( )
A.﹣2 B.2 C.3 D.4
8.(2022·北京市第一六一中学七年级期中)如果代数式与的值互为相反数,则的值为( )
A. B. C. D.
9.(2022·北京十四中七年级期中)如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示).请你运用所学的数学知识来研究,则这7个数的和不可能是( )
A.63 B.70 C.105 D.96
10.(2022·北京市怀柔区桥梓中学七年级阶段练习)有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车,若每辆客车乘43 人, 则只有 1人不能上车,有下列四个等式:
①,②,
③,④,
其中符合题意的是 ( )
A.①②③ B.②③④ C.③④ D.②③
二、填空题
11.(2022·北京海淀·七年级期中)一种商品每件成本为a元,按成本增加25%定价,售出60件,可盈利___________元(用含a的式子表示).
12.(2022·北京市通州区北关中学七年级期中)单项式与是同类项,则___________
13.(2022·北京市第十三中学分校七年级期中)若2是关于的一元一次方程的解,则___________.
14.(2022·北京市第十二中学七年级期中)若 是关于x的一元一次方程,则 ________.
15.(2022·北京二中七年级期中)对于两个不相等的有理数a,b,我们规定符号表示a,b两数中较大的数,例如.按照这个规定,方程的解为_______.
16.(2022·北京市平谷区峪口中学七年级阶段练习)双层游轮的票价是上层票每张12元,下层票每张8元,现在游轮上共有游客150人,而且下层票的总票款比上层票的总票款多700元.那么这艘轮船上下两层游客的人数分别是多少 设这艘邮轮上层的游客人,这艘油轮下层的游客人,可列方程组为__________.
三、解答题
17.(2022·北京市京源学校七年级期中)小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含 的代数式表示地面的总面积 ;
(2)已知 ,且客厅面积是卫生间面积的 倍,如果铺 平方米地砖的平均费用为 元,那么小王铺地砖的总费用为多少元
18.(2022·北京市第十二中学七年级期中)化简:
19.(2022·北京市第三十五中学七年级期中)解方程:
(1);
(2);
(3).
20.(2022·北京市陈经纶中学分校望京实验学校七年级期中)如图,若点A在数轴上对应的数为,点B在数轴上对应的数为b,且,b满足
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
21.(2022·北京市第三十五中学七年级期中)列方程组解应用题
某地需要将一段长为180米的河道进行整修,整修任务由A,B两个工程队先、后接力完成.已知A工程队每天整修12米,B工程队每天整修8米,共用时20天.问A,B两个工程队整修河道分别工作了多少天?
22.(2022·北京师范大学亚太实验学校七年级期中)列方程(组)解决下列问题
某蔬菜公司收购到一批蔬菜,计划用天加工后上市销售,该公司的加工能力是:每天可以精加工吨或者粗加工吨,且每吨蔬菜精加工后的利润为元,粗加工后的利润为元,已知公司售完这批加工后的蔬菜,共获得利润元,求这批蔬菜共多少吨?
23.(2022·北京顺义·七年级期末)某校组织学生参加冬奥会知识竞赛,共设20道单项选择题,各题分值相同,每题必答,下表是部分参赛者的得分统计表:
参赛者 答对题数 答错题数 得分
于潇 20 0 100
王晓林 18 2 88
李毅 10 10 40
… … … …
(1)根据表格提供的数据,答对1题得_______分,答错1题扣________分;
(2)参赛者李小萌得了76分,求她答对了几道题.
24.(2022·北京市陈经纶中学分校七年级期中)某区运动会要印刷秩序册,有两个印刷厂前来联系业务,他们的报价相同,甲厂的优惠条件是:按每份定价6元的八折收费,另收500元制版费;乙厂的优惠条件是:每份定价6元的价格不变,而500元的制版费四折优惠.
问:(1)这个区印制多少份秩序册时两个印刷厂费用是相同的;
(2)当印制200份、400份秩序册时,选哪个印刷厂所付费用较少;为什么.
25.(2022·北京市京源学校七年级期中)将连续的偶数2,4,6,8,…排成如下表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和等于 .
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为x,用代数式表示十字框中的五个数的和是 .
(3)在移动十字框的过程中,若框住的五个数的和等于2020,这五个数从小到大依次 , , , , .
(4)框住的五个数的和能等于2019吗?
26.(2022·北京市第一六一中学七年级期中)如图,在数轴上有A,B两点,且AB=8,点A表示的数为6;动点P从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
(1)写出数轴上点B表示的数是 ;
(2)当t=2时,线段PQ的长是 ;
(3)当0<t<3时,则线段AP= ;(用含t的式子表示)
(4)当PQ=AB时,求t的值.
27.(2022·北京朝阳·七年级期中)如图,在数轴上点A、C、B表示的数分别是-2、1、12.动点P从点A出发,沿数轴以每秒3个单位长度的速度向终点B匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向终点A匀速运动,设点Q的运动时间为t秒.
(1)AB的长为_______;
(2)当点P与点Q相遇时,求t的值.
(3)当点P与点Q之间的距离为9个单位长度时,求t的值.
(4)若PC+QB=8,直接写出t点P表示的数.
28.(2022·北京昌平·七年级期中)【概念学习】
点A,B,C为数轴上的三点,如果点C到A的距离是点C到B的距离的2倍,那么我们就称点C是的偶点.
如图1,点A表示的数为,点B表示的数为1,表示0的点C到点A的距离是2,到点B的距离是1,那么点C是的偶点;表示的点D到点A的距离是1,到点B的距离是2,那么点D就不是的偶点,但点D是的偶点.
【初步探究】
已知如图2,M,N为数轴上两点,点M表示的数为,点N表示的数为5,若点F是的偶点,回答下列问题:
(1)当F在点M,N之间,点F表示的数为__________;
(2)当F为数轴上一点,点F表示的数为____________;
【深入思考】
(3)如图3,P、Q为数轴上两点,点P表示的数为,点Q表示的数为40,现有一个动点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,求当t为何值时,P,Q,E中恰有一个点为其余两点的偶点?
29.(2022·北京市怀柔区桥梓中学七年级阶段练习)把450棵树苗分给一中队、二中队,使两个中队分得的树苗的比是4:5,每个中队各分到树苗多少棵?
参考答案:
1.A
【解析】根据题意可直接列出代数式即可.
解:由题意得:;
故选A.
【点睛】本题主要考查列代数式,读懂题意是解题的关键.
2.B
【解析】直接利用同类项的概念得出n,m的值,再利用绝对值的性质求出答案.
解:∵与是同类项,
∴2m=1,2n=3,
解得:m=,n=,
∴|m﹣n|=|﹣|=1.
故选:B.
【点睛】此题主要考查了同类项,正确把握同类项的定义是解题关键.
3.B
【解析】根据合并同类项法则即可依次判断.
A、5m2﹣4m2=m2,故本选项不合题意;
B、3a2b﹣3ba2=0,故本选项符合题意;
C、3a与2b不是同类项,所以不能合并,故本选项不合题意;
D、2x3与3x2不是同类项,所以不能合并,故本选项不合题意;
故选:B.
【点睛】此题主要考查整式的加减,解题的关键是熟知合并同类项法则.
4.D
【解析】把x=2代入方程3x﹣5=2x+m可得到关于m的方程,解方程可求得m的值.
解:∵x=2是方程3x﹣5=2x+m的解,
∴把x=2代入方程可得6﹣5=4+m,
解得m=﹣3,
故选:D.
【点睛】本题主要考查一元一次方程的解的定义,掌握能使方程左右两边同时成立的未知数的值是方程的解是解题的关键.
5.B
【解析】根据等式的性质判断即可.
解:A、若,当时,两边都除以c无意义,故此选项不符合题意;
B、若,两边都乘以c,得,故此选项符合题意;
C、若,得或,故此选项不符合题意;
D、若,两边都乘以,得,故此选项不符合题意.
故选:B.
【点睛】本题考查等式的基本性质,解决本题的关键是掌握等式的两边同时加上(或减去)同一个数(或式子),等式仍成立;等式的两边同时乘以(或除以)同一个不为零的数(或式子),等式仍成立.
6.C
【解析】根据一元一次方程的定义进行解答即可.
解:①,是一元一次方程,符合题意;
②,含有2个未知数,不是一元一次方程,不合题意;
③,分母含有字母,不是一元一次方程,不合题意;
④,是一元一次方程,符合题意;
⑤,未知数的最高次数是2,不是一元一次方程,不合题意;
⑥,是一元一次方程,符合题意.
综合上分析可得,是一元一次方程的是:①④⑥,
故选:C.
【点睛】本题考查了一元一次方程的定义,只含有一个未知数(元),未知数的次数都是1,等号两边都是整式,这样的方程叫作一元一次方程,能熟记一元一次方程的定义是解此题的关键.
7.D
【解析】先求解关于x的一元一次方程,然后代入求解即可.
解:3x+6=0,
解得:x=-2,
将x=-2代入3x=2-2m中,得,
-6=2-2m,
解得:m=4,
故选:D.
【点睛】题目主要考查解一元一次方程及一元一次方程的解,熟练掌握解一元一次方程是解题关键.
8.D
【解析】利用互为相反数之和为0列出方程,求出方程的解即可得到的值.
解:根据题意,得,
解得:,
故选D.
【点睛】本题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把系数化为1,即可求出解.
9.D
【解析】设“H”型框中的正中间的数为,则其他6个数分别为,,,,,,表示出这7个数之和,然后分别列出方程解答即可.
解:设“H”型框中的正中间的数为x,则其他6个数分别为,,,,,,这7个数之和为: .
由题意得
A.,解得:,能求得这7个数;
B. ,解得:,能求得这7个数;
C.,解得:,能求得这7个数;
D.,解得: ,此时不能求得这7个数.
故选:D.
【点睛】此题考查一元一次方程的实际运用,掌握“H”型框中的7个数的数字的排列规律是解决问题的关键.
10.C
【解析】首先要理解清楚题意,知道总的客车数量及总的人数不变,然后采用排除法进行分析从而得到正确答案.
解:根据总人数列方程,应是,
则④正确,①错误,
根据客车数列方程,应该为,
则③正确,②错误,
则正确的是③,④,
故选C.
【点睛】此题考查了由实际问题抽象出一元一次方程的知识,解题的关键是能够根据不同的等量关系列方程.
11.
【解析】根据利润=售价-进价列出代数式即可.
解:一种商品每件成本为a元,按成本增加25%定价,售出60件,可盈利(元).
故答案为:.
【点睛】本题主要考查了列代数式,解题的关键是熟练掌握利润=售价-进价.
12.
【解析】根据单项式的定义,字母相同且对应字母的指数相同求得的值,进而合并同类项即可求解.
解:∵单项式与是同类项,
∴,
解得
∴
故答案为:
【点睛】本题考查了同类项的定义,合并同类项,掌握同类项的定义求得的值是解题的关键.
13.
【解析】把x=2代入方程即可得到一个关于a的方程,解方程即可求解.
解:把x=2代入方程得,
解得a=.
故答案是:.
【点睛】本题考查了方程的解的定义,解一元一次方程,就是能够使方程左右两边相等的未知数的值.
14.1
【解析】把只含有一个未知数,并且未知数的次数是1的整式方程称为一元一次方程,根据一元一次方程的概念即可完成解答.
由题意得:3-2a=1,
解得:a=1,
故答案为:1.
【点睛】本题考查了一元一次方程的概念,把握一元一次方程的概念要注意三点:①只含一个未知数,即一元;②未知数的次数是1,即一次;③方程两边都是整式.
15.
【解析】根据题意可排除x为非负数的情形,则考虑x正数的情形,然后解一元一次方程即可.
当x为正数时,则,
即x不可能为正数,故x为负数,
所以,
解得;
故答案为:.
【点睛】本题考查了解一元一次方程,关键是弄懂符号的含义,另外要考虑x的取值情况.
16.
【解析】设这艘游轮上层的游客人数为x人,下层的游客人数为y人,根据“游轮上共有游客150人,而且下层票的总票款是上层票的总票款多700元”列方程组求解可得.
这艘邮轮上层的游客人,这艘油轮下层的游客人,由题意得
.
故答案为.
【点睛】本题主要考查二元一次方程组的应用,理解题意找出题目中所蕴含的等量关系是列出方程组求解的关键.
17.(1)S=6m+2n+18;(2) 铺地砖的总费用4500元
【解析】(1)根据总面积等于四个部分矩形的面积之和列式整理即可得解;
(2)根据题意求出m的值,把m,n的值代入计算即可.
(1)S=2n+6m+3×4+2×3=6m+2n+18.
(2)n=1.5时2n=3
根据题意,得6m=8×3=24,
∵铺1平方米地砖的平均费用为100元,
∴铺地砖的总费用为:
100(6m+2n+18)=100×(24+3+18)=4500.
答:铺地砖的总费用4500元.
【点睛】此题考查了列代数式,准确表示出各部分矩形的长和宽是解题的关键.
18.
【解析】先确定多项式中的同类项,再合并同类项即可.
解:原式
.
【点睛】本题考查的是合并同类项,掌握“同类项的含义与合并同类项的法则”是解本题的关键.
19.(1)
(2)
(3)
【解析】(1)移项,解方程即可.
(2)先去括号,后依次求解即可.
(3)先去分母,再去括号,后依次求解即可.
(1)解:,
移项,得
,
合并同类项,得
,
系数化为1,得
.
(2)解:
去括号,得
移项,得
,
合并同类项,得
,
系数化为1,得
.
(3)解:,
去分母,得
去括号,得
移项,得
,
合并同类项,得
.
【点睛】本题考查了一元一次方程的解法,熟练掌握解方程的基本步骤是解题的关键.
20.(1)AB=3.
(2)P所对应的数是﹣3或﹣1.
(3)不随t的变化而变化,其常数值为2.
试题分析:(1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数;
(3)用含有t的代数式表示出AB和BC,求差即可.
试题解析:(1)∵|a+2|+(b﹣1)2=0,
∴a=﹣2,b=1,
∴AB=b﹣a=1﹣(﹣2)=3.
(2)2x﹣1=x+2,
解得:x=2,
由题意得,点P只能在点B的左边,
①当点P在AB之间时,x+2+1﹣x=2﹣x,
解得:x=﹣1;
②当点P在A点左边时,﹣2﹣x+1﹣x=2﹣x,
解得:x=﹣3,
综上可得P所对应的数是﹣3或﹣1.
(3)t秒钟后,A点位置为:﹣2﹣t,B点的位置为:1+4t, C点的位置为:2+9t
BC=2+9t﹣(1+4t)=1+5t AB=5t+3
AB﹣BC=5t+3﹣(5t+1)=2
所以不随t的变化而变化,其常数值为2.
考点:一元一次方程的应用.
21.A工程队整修河道工作了5天,则B工程队整修河道工作了15天.
【解析】设A工程队整修河道工作了x天,则B工程队整修河道工作了(20-x)天,根据题意,列出方程,即可求解.
解:设A工程队整修河道工作了x天,则B工程队整修河道工作了(20-x)天,根据题意得:
,
解得:,
∴20-x=15,
答:A工程队整修河道工作了5天,则B工程队整修河道工作了15天.
【点睛】本题主要考查了一元一次方程的应用,明确题意,准确得到等量关系是解题的关键.
22.吨
【解析】设精加工天,则粗加工天,利用总利润精加工的天数粗加工的天数,即可得出关于的一元一次方程,解之即可得出的值,再将其代入中即可求出结论.
解:设精加工天,则粗加工天,
依题意得:,
解得:,
.
答:这批蔬菜共吨.
【点睛】本题考查一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
23.(1)答对1题得5分,答错1题扣1分;
(2)她答对16道题.
【解析】(1)先根据于潇的得分可得出答对1题得5分,再根据王晓林的得分即可得出答错1题扣的分数;
(2)设参赛者李小萌答对了道题,从而可得她答错了道题,根据(1)的结果和“参赛者李小萌得了76分”建立方程,解方程即可得.
(1)
解:答对1题得的分数为(分),
答错1题扣的分数为(分),
故答案为:5,1;
(2)
解:设参赛者李小萌答对了道题,则她答错了道题,
由题意得:,
解得,
答:她答对了16道题.
【点睛】本题考查了有理数加减乘除的应用、一元一次方程的应用,正确建立方程是解题关键.
24.(1)250份;(2)当印制200份秩序册时,选乙印刷厂所付费用较少;当印制400份秩序册时选甲印刷厂所付费用较少,理由见解析.
【解析】(1)设要印制x份节目单,则甲厂的收费为500+6×0.8x元,乙厂的收费为6x+500×0.4元,根据费用相同列方程即可解答;
(2)把x=200分别代入甲厂费用500+6×0.8x和乙厂费用6x+500×0.4,比较得出答案. 同样再把x=400分别代入计算比较.
解:(1)设这个区要印制x份秩序册时费用是相同的,根据题意得,
500+6×0.8x=6x+500×0.4,
解得x=250,
答:要印制250份秩序册时费用是相同的.
(2)当印制200份秩序册时:
甲厂费用需:0.8×6×200+500=1460(元),
乙厂费用需:6×200+500×0.4=1400(元),
因为1400<1460,
故选乙印刷厂所付费用较少.
当印制400份秩序册时:
甲厂费用需:0.8×6×400+500=2420(元),
乙厂费用需:6×400+500×0.4=2600(元),
因为2420<2600,
故选甲印刷厂所付费用较少.
【点睛】本题考查了列一元一次方程解决实际问题,一般步骤是: ①审题,找出已知量和未知量;②设未知数,并用含未知数的代数式表示其它未知量;③找等量关系,列方程;④解方程;⑤检验方程的解是否符合题意并写出答案.
25.(1)80;(2)5x;(3)这五个数分别为:394,402,404,406,414;(4)不能
【解析】(1)根据有理数的加法法则计算;
(2)根据图中数字的规律分别表示另外四个数,列式计算即可;
(3)根据(2)列方程5x=2020,求解即可;
(4)列方程5x=2019,求解判断即可.
解:(1)6+14+16+18+26=80,
故答案为:80;
(2)设中间的数为x,则其他四个数分别为x-10,x-2,x+2,x+10,
∴这五个数的和是x-10+x-2+x+x+2+x+10=5x,
故答案为:5x;
(3)由(2)得,设中间的数为x,则这五个数的和是5x,
∴5x=2020,
解得x=404,
∴这五个数分别为:394,402,404,406,414;
故答案为:394,402,404,406,414;
(4)由(2)得,设中间的数为x,则这五个数的和是5x,
∴5x=2019,
解得,
∵x是整数且为偶数,
∴框住的五个数的和不能等于2019.
【点睛】此题考查有理数的加法法则,列代数式的实际应用,解一元一次方程,熟练掌握各知识点并应用解决问题是解题的关键.
26.(1)14;(2)4;(3)6﹣2t;(4)t的值是4或8
【解析】(1)根据两点间的距离公式即可求出数轴上点B表示的数;
(2)先求出当t=2时,P点对应的有理数为2×2=4,Q点对应的有理数为6+1×2=8,再根据两点间的距离公式即可求出PQ的长;
(3)先求出当0<t<3时,P点对应的有理数为2t<6,再根据两点间的距离公式即可求出AP的长;
(4)由于t秒时,P点对应的有理数为2t,Q点对应的有理数为6+t,根据两点间的距离公式得出PQ=|2t﹣(6+t)|=|t﹣6|,根据PQAB列出方程,解方程即可求解.
(1)6+8=14.
故数轴上点B表示的数是14;
(2)当t=2时,P点对应的有理数为2×2=4,Q点对应的有理数为6+1×2=8,
8﹣4=4.
故线段PQ的长是4;
(3)当0<t<3时,P点对应的有理数为2t<6,
故AP=6﹣2t;
(4)根据题意可得:
|t﹣6|8,
解得:t=4或t=8.
故t的值是4或8.
【点睛】本题考查了一元一次方程的应用和数轴,解答本题的关键是掌握点的移动与点所表示的数之间的关系,(4)中解方程时要注意分两种情况进行讨论.
27.(1)14
(2)当t为秒时,点P与点Q相遇;
(3)当t为1秒或秒时,点P与点Q间的距离为9个单位长度;
(4)存在某一时刻使得PC+QB=8,此时点P表示的数为.
【解析】(1)根据两点之间的距离公式直接求出AB的长;
(2)当运动时间为t秒时,点P表示的数为3t-2,点Q表示的数为-2t+12;由点P,Q相遇,即可得出关于t的一元一次方程,解之即可得出结论;
(3)由PQ=9,即可得出关于t的一元一次方程,解之即可得出结论;
(4)当运动时间为t秒时,点P表示的数为3t-2,PC=|3t-2-1|=|3t-3|,QB=2t,由PC+QB=8,即可得出关于t的一元一次方程,解之即可得出t的值,再将其代入3t-2中即可求出结论.
(1)
解:AB=12-(-2)=14,
故答案为:14;
(2)
解:当运动时间为t秒时,点P表示的数为3t-2,点Q表示的数为-2t+12.
依题意得:3t-2=-2t+12,
解得:t=.
答:当t为秒时,点P与点Q相遇;
(3)
解:依题意得:-2t+12-(3t-2)=9或3t-2-(-2t+12)=9,
解得:t=1或t=.
答:当t为1秒或秒时,点P与点Q间的距离为9个单位长度;
(4)
解:当运动时间为t秒时,点P表示的数为3t-2,PC=|3t-2-1|=|3t-3|,QB=2t.
依题意得:|3t-3|+2t=8,
即3-3t+2t=8或3t-3+2t=8,
解得:t=-5(不合题意,舍去)或t=,
∴3t-2=.
答:存在某一时刻使得PC+QB=8,此时点P表示的数为.
【点睛】本题考查了一元一次方程的应用以及数轴,解题的关键是:(1)利用数轴上两点间的距离,找出点B,C表示的数;(2)找准等量关系,正确列出一元一次方程;(3)找准等量关系,正确列出一元一次方程;(4)找准等量关系,正确列出一元一次方程.
28.(1)3;
(2)3或11;
(3)10秒、15秒或20秒.
【解析】(1)根据偶点的定义,列方程求解即可;
(2)根据题意,分两种情况,分别列方程求解即可;
(3)根据题意,分四种情况分类讨论:①当点E是的偶点时,;②当点E是的偶点时,;③当点Q是的偶点时,;④点P是的偶点时,;然后分别列方程求解得解.
(1)解: 设点F表示的数是x,
点F是的偶点,F在点M,N之间,
即,
即点F表示的数是3;
故答案为:3.
(2)解:设点F表示的数是x,依题,得
或
解得:或11;
故答案为:3或11.
(3)解:点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,则动点E的表示的数为, ,.
分四种情况讨论:
①当点E是的偶点时,,
,
解得:(秒);
②当点E是的偶点时,,
,
解得:(秒);
③当点Q是的偶点时,,
,
解得:(秒);
④点P是的偶点时,,
,
解得:(秒)
综上所述,当为10秒、15秒或20秒时,E、P、Q中恰有一个点为其余两点的偶点.
【点睛】此题考查了数轴上的动点问题与一元一次方程的应用,准确读懂题意、理解偶点的定义、找出正确的等量关系是解此题的关键.
29.一中队、二中队分到树苗200棵、250棵.
【解析】根据总量是450棵树苗,是按照两个中队分得树苗的比为4:5进行分配的,先求出两个中队分得树苗的总份数,进一步求出一份树苗数的数量,最后分别求得每个中队分到树苗的棵数.
解:450÷(4+5)=50
一中队:4×50=200棵
二中队:5×50=250棵
答:一中队、二中队分到树苗200棵、250棵.
考点:比例的应用题.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
