2022-2023学年上学期京改版数学七年级上册(北京地区)第三章 简单的几何图形 期末综合复习题 (含解析)
文档属性
| 名称 | 2022-2023学年上学期京改版数学七年级上册(北京地区)第三章 简单的几何图形 期末综合复习题 (含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 14:17:11 | ||
图片预览




文档简介
第三章 简单的几何图形 期末综合复习题
一、单选题
1.(2022·北京房山·七年级期中)直径为60厘米的圆,在生活中可能是( )
A.杯盖的面 B.井盖的面
C.一元硬币的面 D.蒙古包占地的面
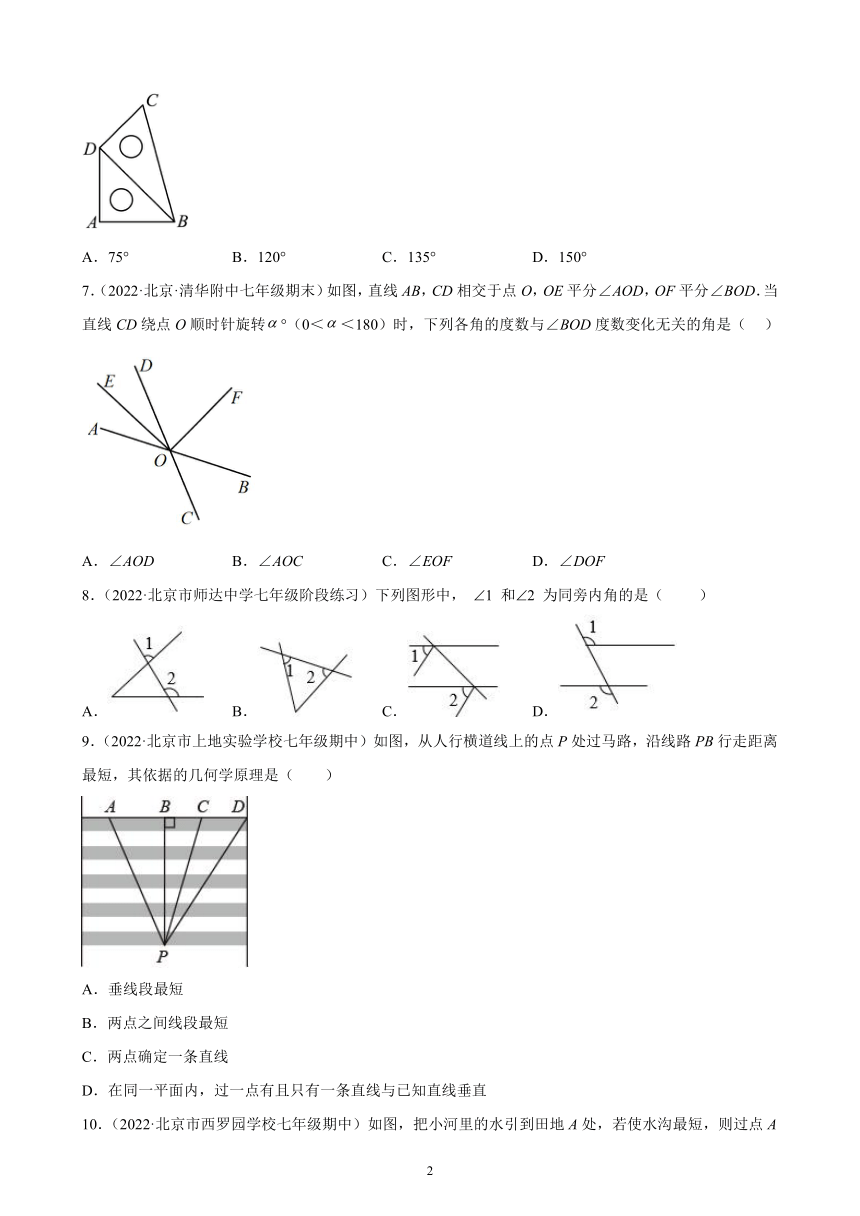
2.(2022·北京房山·七年级期末)下列几何体中,是圆锥的为( )
A. B. C. D.
3.(2022·北京通州·七年级期末)如图是一个正方体的平面展开图,每个面上都标有一个汉字,将其折成一个正方体,与“起”字相对的面上的汉字为( )
A.走 B.向 C.未 D.来
4.(2022·北京通州·七年级期末)下列几何体中,从正面看为三角形的是( )
A. B. C. D.
5.(2022·北京市怀柔区桥梓中学七年级阶段练习)下列说法正确的是( )
A.一个数不是正数就是负数
B.大于的角都是钝角
C.是6的倍数的数也一定是3的倍数
D.5千克盐溶解在100千克水中,盐水的含盐率是5%.
6.(2022·北京房山·七年级期末)将一副直角三角板如图所示摆放,则图中的大小为( )
A.75° B.120° C.135° D.150°
7.(2022·北京·清华附中七年级期末)如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转°(0<<180)时,下列各角的度数与∠BOD度数变化无关的角是( )
A.∠AOD B.∠AOC C.∠EOF D.∠DOF
8.(2022·北京市师达中学七年级阶段练习)下列图形中, 1 和2 为同旁内角的是( )
A. B. C. D.
9.(2022·北京市上地实验学校七年级期中)如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
10.(2022·北京市西罗园学校七年级期中)如图,把小河里的水引到田地A处,若使水沟最短,则过点A向河岸l作垂线,垂足为点B,沿AB挖水沟即可,理由是( )
A.两点之间,线段最短 B.垂线段最短
C.两点确定一条直线 D.过一点可以作无数条直线
11.(2022·北京四中璞瑅学校七年级期中)下列语句正确的有( )
①量出直线外一点到直线的距离;
②在同一平面内,两条不同直线有且只有一个公共点
③从直线外一点到这条直线的垂线段叫作直线的距离
④两条直线有相交、垂直、平行三种位置关系
A.个 B.个 C.个 D.个
12.(2022·北京交通大学附属中学七年级期中)直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
A.60° B.50° C.40° D.30°
二、填空题
13.(2022·北京顺义·七年级期末)如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的_______.(填序号)
14.(2022·北京怀柔·七年级期末)若AB=6cm,点C是直线AB上一点,BC=2cm,D是线段AC的中点,则线段AD的长度为__________cm.
15.(2022·北京·101中学七年级期中)如图,已知线段上有两点C,D,且,E,F分刟为,的中点,,则______.
16.(2022·北京房山·七年级期末)如图,将两块三角板的直角顶点重合后重叠在一起,若,则=______°,依据是______.
17.(2022·北京海淀·七年级期末)如图,一艘货轮B在沿某小岛O北偏东60°方向航行中,发现了小岛O的东南方向一座灯塔A.某一时刻,灯塔A与货轮B分别到小岛O的距离恰好相等,用量角器度量得到此时的度数是______°(精确到度).
18.(2022·北京铁路二中七年级开学考试)如图,OB,OC分别是,的三等分线,若,则的度数为______.
19.(2022·北京·和平街第一中学七年级期中)如图,直线a、b相交于点O,若∠1=30°,则∠2=___
20.(2022·北京市怀柔区第五中学七年级期末)小东同学做了直角三角形模具,如图所示.在AC,BC,AB三边中,根据______________,可知___________最长.
21.(2022·北京东城·七年级期末)如图,在三角形中,,,,,则点到的距离等于______.
22.(2022·北京·北师大实验中学七年级期中)将一副三角板和一个直尺按如图所示的位置摆放,则的度数为____________度.
三、解答题
23.(2022·北京东城·七年级期末)如图,点A,B,C不在同一条直线上.
(1)画直线AB;
(2)尺规作图:作射线CF交直线AB于点D,使得(不写作法,保留作图痕迹).
24.(2022·北京门头沟·七年级期末)已知直线MN上有一线段AB,AB=6,点C是线段AB的中点,点D在直线MN上,且BD=2,求线段DC的长.
25.(2022·北京东城·七年级期末)如图,A地和B地都是海上观测站,从A地发现它的东北方向(北偏东45°)有一艘船.同时,从B地发现这艘船在它的北偏西60°方向.在图中画出这艘船的位置O.(保留作图痕迹)
26.(2022·北京怀柔·七年级期末)如图,平面内有两个点A,B.应用量角器、圆规和带刻度的直尺完成下列画图或测量:
(1)经过A,B两点画直线,写出你发现的基本事实;
(2)利用量角器在直线AB一侧画;
(3)在射线BC上用圆规截取BD=AB(保留作图痕迹);
(4)连接AD,取AD中点E,连接BE;
(5)通过作图我们知道.,观察并测量图形中的角,写出一组你发现的两个角之间可能存在的数量关系.
27.(2022·北京延庆·七年级期末)已知:∠AOB,过点O引两条射线OC,OM,且OM平分.
(1)如图,若∠AOB=120°,∠BOC=30°,且点C在∠AOB的内部.
①请补全图形;
②求出∠MOB的度数;
以下是求∠MOB的度数的解题过程,请你补充完整.
解:∵∠AOC=∠AOB-∠BOC,∠AOB=120°,∠BOC=30°,
∴∠AOC= 90°.
∵OM平分,
∴∠MOC= = °.
∵∠MOB=∠MOC+ ,
∴∠MOB= °.
(2)若∠AOB=α,∠BOC=β(其中α<β<90°),画出图形并直接写出∠MOB的度数.(用含α,β的式子表示)
28.(2022·北京四中璞瑅学校七年级期中)如图,在一片农田附近有一条小河.因为干旱,附近的农民们常常需要从河中引水灌溉农田.张伯伯家的农田位于图中点处,他也想挖一条水渠,把河水引到自家农田处.
(1)请问,张伯伯如何挖渠才能使渠道最短?请你在如图中画出来.
(2)你这样画的依据是什么?
(3)如果图中比例尺为:,水渠大概要挖多长?
(4)请你举出一个生活中应用以上“依据”的实际例子.
29.(2022·北京密云·七年级期末)如图,直线,E为直线CD上一点,射线EH交直线AB于点F.
(1)按要求画图:
①利用量角器及直尺,画∠FED的角平分线EM,交直线AB于点N;
②过点N作NP⊥CD,垂足为P.
(2)完成下列填空:
比较线段NE和NP的大小,可以得到NE____________NP;(填“>”、“=”或“<”)理由是____________.
30.(2022·北京·七年级期中)如图,点A在的一边上.按下列要求画图:
(1)过点A画直线,与的另一边相交于点B;
(2)过点A画的垂线段,垂足为点C;
(3)过点C画直线∥,交直线于点D;
参考答案:
1.B
【解析】根据题意,直径为60厘米,在生活中可能是井盖的面的大小,据此解答即可.
解:杯盖的面、一元硬币的面都小于直径60厘米的圆,蒙古包的占地面积大于直径60厘米的圆,只有井盖的面接近直径60厘米的圆.
故选:B.
【点睛】此题考查了认识平面图形,要注意联系实际,计量单位和数据的大小,灵活选择.
2.C
【解析】根据每一个几何体的特征即可判断.
解:A是圆柱体;
B是正方体;
C是圆锥;
D是四棱锥;
故选:C
【点睛】本题考查了认识立体图形,熟练掌握每一个几何体的特征是解题的关键.
3.D
【解析】通过空间想象,将展开图还原成立体图,再去推测每个面及其对面的汉字是什么.
折叠后:“一”和 “向”相对;
“起”和“来”相对;
“走”和“未”相对;
故A、B、C均不对;D对,符合题意;
故选D
【点睛】本题考查正方体相对两面上字,展开空间想象找到每个字对面的字是关键.
4.C
【解析】逐一分析从正面看到的图形即可解题.
A.从正面看是长方形,故A不符合题意;
B. 从正面看是长方形形,故B不符合题意;
C. 从正面看是是三角形,故C符合题意;
D. 从正面看是两个长方形拼成的几何图形,故D不符合题意.
故选:C.
【点睛】本题考查从正面看几何体,是基础考点,掌握相关知识是解题关键.
5.C
【解析】根据数的分类、钝角的定义、倍数的性质和含盐率公式逐一判断即可.
解:A. 一个数除了正数和负数外,还有可能是0,故本选项错误;
B. 大于且小于180°的角都是钝角,缺少条件,故本选项错误;
C. 是6的倍数的数也一定是3的倍数,故本选项正确;
D. 5千克盐溶解在100千克水中,盐水的含盐率是5÷(100+5)≈%,故本选项错误.
故选C.
【点睛】此题考查的是数的分类、钝角的定义、倍数的性质和求含盐率,掌握数的分类、钝角的定义、倍数的性质和含盐率公式是解决此题的关键.
6.C
【解析】根据题意得:∠ADB=45°,∠BDC=90°,从而得到∠ADC=∠ADB+∠BDC=135°,即可求解.
解:根据题意得:∠ADB=45°,∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
故选:C
【点睛】本题主要考查了直角三角板中角的计算,熟练掌握一副直角三角板中每个角的度数是解题的关键.
7.C
【解析】根据角平分线的定义可得∠AOD=2∠EOD,∠BOD=2∠DOF,结合平角的定义可求解∠EOF=90°,由∠EOF的度数为定值可判定求解.
解:∵OE平分∠AOD,OF平分∠BOD,
∴∠AOD=2∠EOD,∠BOD=2∠DOF,
∵∠AOD+∠BOD=180°,
∴∠EOD+∠DOF=90°,
即∠EOF=90°,
∴直线CD绕点O顺时针旋转α°(0<α<180)时,∠EOF的度数与∠BOD度数变化无关.
故选:C.
【点睛】本题主要考查角平分线的定义,求解∠EOF的度数是解题的关键.
8.B
【解析】首先弄清各图中,∠1,∠2是哪两条直线被另一条直线所截形成的角;接下来根据互为同旁内角的两角的位置特点,进行判别即可.
解:A.∠1,∠2在截线的同旁,在两条被截线同方向,是同位角,故选项A不合题意;
B.∠1,∠2在截线的同旁,夹在两条被截线同旁是同旁内角,故选项B符合题意;
C.∠1,∠2不是两条直线被第三条直线在截线的角,不是同位角,内错角,同旁内角,故选项C不合题意;
D.∠1,∠2截线两侧,在两被截直线的外部形成的角,所以不是同旁内角(也不是同位角,更不是内错角)故选项D不合题意.
故选B.
【点睛】本题考查了同位角、同旁内角、内错角,熟悉掌握定义是解题关键.
9.A
【解析】利用垂线段最短的原理即可判断.
解:从人行横道线上的点P处过马路,沿线路PB行走且,所以由垂线段最短的原理可以知,沿线路PB行走距离最短,
故选:A.
【点睛】本题考查了垂线段最短的原理,解题的关键是:掌握垂线段最短的原理.
10.B
【解析】根据题意抽象为过直线外一点到直线的距离最短分析即可
根据题意,小河可以抽象为一条直线,点到直线的所有连线中,垂线段最短
理由是: 垂线段最短
故选B
【点睛】本题考查了垂线段最短的应用,理解题意是解题的关键.
11.A
【解析】根据点到直线的距离、平面内两直线的位置关系求解即可.
量出直线外一点到直线的垂线段的长度即为点到直线的距离,
故正确;
在同一平面内,两条不同直线有一个公共点或没有公共点,
故错误;
从直线外一点到这条直线的垂线段的长度叫作点到直线的距离,
故错误;
同一平面内两条直线有相交、平行两种位置关系,
故错误;
故选:.
【点睛】此题考查了平面内两直线的位置关系、点到直线的距离,熟练掌握平面内两直线的位置关系、点到直线的距离是解题的关键.
12.C
【解析】过E作EF∥AB CD,由平行线的质可得∠1=∠3,∠2=∠4, ∠3+∠4=∠1+∠2,根据三角形内角和可得: ∠3+∠4=60°,从而可得: ∠1+∠2=60°,由∠1=20°,可得: ∠2=40°.
如图,过E作EF∥AB,
则AB∥EF∥CD,
∴∠1=∠3,∠2=∠4,
∵∠3+∠4=60°,
∴∠1+∠2=60°,
∵∠1=20°,
∴∠2=40°,
故选C.
【点睛】本题考查了平行线的性质,解决本题的关键是要正确作出辅助线和熟练掌握平行线的性质.
13.②⑤
【解析】结合题意,根据简单几何体展开图的性质对各个选项逐个分析,即可得到答案.
根据题意,再剪开一条棱,展开图不可能为:
故答案为:②⑤.
【点睛】本题考查了几何体展开图的知识;解题的关键是熟练掌握简单几何体展开图的性质,从而完成求解.
14.2或4##4或2
【解析】分点C在线段AB上和点C在线段AB的延长线上两种情况考虑,利用中点及线段和差关系即可求得AD的长度.
当点C在线段AB上时,如图:
∵AB=6cm,BC=2cm
∴AC=AB-BC=6-2=4(cm)
∵D是线段AC的中点
∴
当点C在线段AB的延长线上时,如图:
∵AC=AB+BC=6+2=8(cm)
∵D是线段AC的中点
∴
故答案为:2或4
【点睛】本题考查了中点的意义及线段的和差关系,涉及分类讨论.
15.3.6
【解析】首先设AC=2xcm,则线段CD=3xcm,DB=4xcm,然后根据E、F分别是线段AC、DB的中点,分别用x表示出EC、DF,根据EF=2.4cm,求出x的值,即可求出线段AB的长是多少.
设AC=2x,则线段CD=3x,DB=4x,
∵E、F分别是线段AC、DB的中点,
∴EC=AC=x,DF=DB=2x,
∵EF=EC+CD+DF=x+3x+2x=2.4,
∴x=0.4,
∴AB=9x=9×0.4=3.6(cm),
故答案为:3.6.
【点睛】此题主要考查了两点间的距离的求法,以及线段的中点的特征和应用,要熟练掌握.
16. 42 同角的余角相等
【解析】由同角的余角相等可得∠2=∠1=42°.
解:如图,
∵将两块三角板的直角顶点重合后叠放在一起,
∴∠1+∠3=∠2+∠3=90°,
∴∠2和∠1都是∠3的余角,
∴∠2=∠1=42°,
故答案为:42,同角或等角的余角相等.
【点睛】本题考查了同角或等角的余角相等,看懂图形是解题的关键.
17.53
【解析】根据图形,利用量角器直接测量即可.
如图,经用量角器测量得到∠ABO=53°
故答案为:53.
【点睛】本题考查方位角和角的测量,是基础题.
18.
【解析】由角的三等分线的含义先求解 再结合角的三等分线可得从而可得答案.
解: ,OB是的三等分线,
OC分别是的三等分线,
故答案为:
【点睛】本题考查的是角的三等分线的应用,结合角的和差关系理解图形中的三等分线是解本题的关键.
19.30°
因∠1和∠2是邻补角,且∠1=30°,由邻补角的定义可得∠2=180°﹣∠1=180°﹣30°=150°.
解:∵∠1+∠2=180°,
又∠1=30°,
∴∠2=150°.
20. 垂线段最短 AB
【解析】根据垂线段最短即可求解.
解:∵AC⊥BC,
∴AC<AB,BC<AB,
∴AB最长.
即在AC,BC,AB三边中,根据垂线段最短,可知AB最长.
故答案为:垂线段最短,AB.
【点睛】本题考查了垂线的性质,掌握垂线段最短是解题的关键.
21.3
【解析】点到直线的距离是指过直线外一点向直线做的垂线段的长度,根据定义可以得出答案.
解:∵,
∴AC⊥BC,
∴线段AC的长度就是点A到BC的距离,
∵AC=3,
∴点A到的距离等于3.
故答案为:3.
【点睛】本题主要考查的是点到直线的距离,属于基础题型.解决这个问题的关键就是要明白点到直线距离的定义.
22.75
【解析】首先计算的度数,再根据平行线的性质可得,进而可得答案.
解:∵,,
∴,
∵,
∴,
故答案为:75.
【点睛】此题主要考查了平行线的性质,掌握平行线的性质并能灵活应用是解题关键.
23.(1)见解析
(2)见解析
【解析】(1)让直尺的边沿同时过A,B两点,画直线即可;
(2)分点D在点B的右侧和左侧两种情形画图.
(1)
画图如下:
(2)
画图如下:
【点睛】本题考查了直线,射线,线段的基本画图,正确使用直尺,灵活进行分类是解题的关键.
24.1或5
【解析】根据题意,分两种情况:(1)点D在点B的右侧时,(2)点D在点B的左侧时,求出线段DC的长度是多少即可.
解:
∵点C是AB的中点,
∴.
∵AB=6,
当点D在点B左侧时;
∵DB=2,
∴
当点D在点B右侧时;
.
【点睛】本题考查了利用中点性质转化线段之间倍分关系,从而求出线段的长短.解题的关键是在不同情况下灵活运用它的不同表示方法,同时灵活运用线段的和差倍分转化线段之间的数量关系也是十分关键的一点.
25.见解析
【解析】利用方向角分别得出北偏东45°方向以及北偏西60°方向的位置产生的交点即为所求.
解:如图所示:先作北偏东45°方向的射线AO,然后作北偏西60°方向的射线BO,两条射线交于点O,点O即为这艘船的位置.
【点睛】此题主要考查了应用设计与作图,正确掌握方向角的确定方法是解题关键.
26.(1)画图见解析,基本事实:两点确定一条直线;(2)画图见解析;(3)画图见解析;(4)画图见解析;(5)
【解析】(1)直接过AB两点画直线即可;
(2)用量角器直接画图即可;
(3)以B为圆心,BA长度为半径画圆即可;
(4)用带刻度的直尺量出AD长度取中点即可;
(5)用量角器测量各个角度大小即可;
(1)画图如下,基本事实:两点确定一条直线
(2)画图如下;
(3)画图如下;
(4)画图如下;
(5)不唯一,正确即可.
例如:,,等
或
【点睛】本题考查线段和角度作图,熟练使用量角器、圆规和带刻度的直尺是解题的关键.
27.(1)①见解析;②,45,∠COB,75
(2)见解析,或
【解析】(1)①根据题意作图即可;
②利用角平分线计算得,再结合图形计算即可得;
(2)分两种情况讨论,如解析中图象所示,分别利用角平分线进行计算即可得.
(1)
①根据题意,作图如下:
②解:∵,,,
∴.
∵OM平分,
∴,
∵,
∴;
故答案为:;;;;
(2)
解:分两种情况讨论:
①如图所示:,,
∴,
∴,
∴;
②如图所示:,,
∴,
∴,
∴;
综上可得:或.
【点睛】题目主要考查角平分线的计算,理解题意,充分利用角平分线进行计算是解题关键.
28.(1)见解析;
(2)垂线段最短;
(3)水渠大概要挖米;
(4)体育课上测量跳远成绩的依据也是利用垂线段最短.
【解析】(1)作PH⊥CD即可;
(2)根据垂线段最短解决问题;
(3)测量出PH的长,再利用比例尺求出实际距离;
(4)体育课上测量跳远成绩的依据也是利用垂线段最短.
(1)
解:如图,作,线段即为所求;
(2)
解:画图的依据是垂线段最短.
(3)
解: ,
∴实际距离为m,
水渠大概要挖m;
(4)
解:体育课上测量跳远成绩的依据也是利用垂线段最短.
【点睛】本题考查作图—应用与设计作图,垂线段最短,比例尺等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
29.(1)见解析
(2)>;垂线段最短
【解析】(1)①利用量角器及直尺可直接进行作图;②根据垂线可进行作图;
(2)根据垂线段最短可进行求解.
(1)
解:如图所示:
(2)
解:比较线段NE和NP的大小,可以得到NE>NP;理由是垂线段最短;
故答案为>,垂线段最短.
【点睛】本题主要考查尺规作图及垂线段最短,熟练掌握垂线的作图及垂线段最短是解题的关键.
30.(1)见解析
(2)见解析
(3)见解析
【解析】(1)根据垂线的定义作图即可;
(2)根据垂线段的定义作图即可;
(3)根据平行线的定义作图即可.
(1)
如图,直线AB即为所求.
(2)
如图,垂线段即为所求.
(3)
如图,直线CD即为所求.
【点睛】本题考查了作图,涉及垂线、垂线段及平行线,熟练掌握知识点是解题的关键.
一、单选题
1.(2022·北京房山·七年级期中)直径为60厘米的圆,在生活中可能是( )
A.杯盖的面 B.井盖的面
C.一元硬币的面 D.蒙古包占地的面
2.(2022·北京房山·七年级期末)下列几何体中,是圆锥的为( )
A. B. C. D.
3.(2022·北京通州·七年级期末)如图是一个正方体的平面展开图,每个面上都标有一个汉字,将其折成一个正方体,与“起”字相对的面上的汉字为( )
A.走 B.向 C.未 D.来
4.(2022·北京通州·七年级期末)下列几何体中,从正面看为三角形的是( )
A. B. C. D.
5.(2022·北京市怀柔区桥梓中学七年级阶段练习)下列说法正确的是( )
A.一个数不是正数就是负数
B.大于的角都是钝角
C.是6的倍数的数也一定是3的倍数
D.5千克盐溶解在100千克水中,盐水的含盐率是5%.
6.(2022·北京房山·七年级期末)将一副直角三角板如图所示摆放,则图中的大小为( )
A.75° B.120° C.135° D.150°
7.(2022·北京·清华附中七年级期末)如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转°(0<<180)时,下列各角的度数与∠BOD度数变化无关的角是( )
A.∠AOD B.∠AOC C.∠EOF D.∠DOF
8.(2022·北京市师达中学七年级阶段练习)下列图形中, 1 和2 为同旁内角的是( )
A. B. C. D.
9.(2022·北京市上地实验学校七年级期中)如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
10.(2022·北京市西罗园学校七年级期中)如图,把小河里的水引到田地A处,若使水沟最短,则过点A向河岸l作垂线,垂足为点B,沿AB挖水沟即可,理由是( )
A.两点之间,线段最短 B.垂线段最短
C.两点确定一条直线 D.过一点可以作无数条直线
11.(2022·北京四中璞瑅学校七年级期中)下列语句正确的有( )
①量出直线外一点到直线的距离;
②在同一平面内,两条不同直线有且只有一个公共点
③从直线外一点到这条直线的垂线段叫作直线的距离
④两条直线有相交、垂直、平行三种位置关系
A.个 B.个 C.个 D.个
12.(2022·北京交通大学附属中学七年级期中)直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
A.60° B.50° C.40° D.30°
二、填空题
13.(2022·北京顺义·七年级期末)如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的_______.(填序号)
14.(2022·北京怀柔·七年级期末)若AB=6cm,点C是直线AB上一点,BC=2cm,D是线段AC的中点,则线段AD的长度为__________cm.
15.(2022·北京·101中学七年级期中)如图,已知线段上有两点C,D,且,E,F分刟为,的中点,,则______.
16.(2022·北京房山·七年级期末)如图,将两块三角板的直角顶点重合后重叠在一起,若,则=______°,依据是______.
17.(2022·北京海淀·七年级期末)如图,一艘货轮B在沿某小岛O北偏东60°方向航行中,发现了小岛O的东南方向一座灯塔A.某一时刻,灯塔A与货轮B分别到小岛O的距离恰好相等,用量角器度量得到此时的度数是______°(精确到度).
18.(2022·北京铁路二中七年级开学考试)如图,OB,OC分别是,的三等分线,若,则的度数为______.
19.(2022·北京·和平街第一中学七年级期中)如图,直线a、b相交于点O,若∠1=30°,则∠2=___
20.(2022·北京市怀柔区第五中学七年级期末)小东同学做了直角三角形模具,如图所示.在AC,BC,AB三边中,根据______________,可知___________最长.
21.(2022·北京东城·七年级期末)如图,在三角形中,,,,,则点到的距离等于______.
22.(2022·北京·北师大实验中学七年级期中)将一副三角板和一个直尺按如图所示的位置摆放,则的度数为____________度.
三、解答题
23.(2022·北京东城·七年级期末)如图,点A,B,C不在同一条直线上.
(1)画直线AB;
(2)尺规作图:作射线CF交直线AB于点D,使得(不写作法,保留作图痕迹).
24.(2022·北京门头沟·七年级期末)已知直线MN上有一线段AB,AB=6,点C是线段AB的中点,点D在直线MN上,且BD=2,求线段DC的长.
25.(2022·北京东城·七年级期末)如图,A地和B地都是海上观测站,从A地发现它的东北方向(北偏东45°)有一艘船.同时,从B地发现这艘船在它的北偏西60°方向.在图中画出这艘船的位置O.(保留作图痕迹)
26.(2022·北京怀柔·七年级期末)如图,平面内有两个点A,B.应用量角器、圆规和带刻度的直尺完成下列画图或测量:
(1)经过A,B两点画直线,写出你发现的基本事实;
(2)利用量角器在直线AB一侧画;
(3)在射线BC上用圆规截取BD=AB(保留作图痕迹);
(4)连接AD,取AD中点E,连接BE;
(5)通过作图我们知道.,观察并测量图形中的角,写出一组你发现的两个角之间可能存在的数量关系.
27.(2022·北京延庆·七年级期末)已知:∠AOB,过点O引两条射线OC,OM,且OM平分.
(1)如图,若∠AOB=120°,∠BOC=30°,且点C在∠AOB的内部.
①请补全图形;
②求出∠MOB的度数;
以下是求∠MOB的度数的解题过程,请你补充完整.
解:∵∠AOC=∠AOB-∠BOC,∠AOB=120°,∠BOC=30°,
∴∠AOC= 90°.
∵OM平分,
∴∠MOC= = °.
∵∠MOB=∠MOC+ ,
∴∠MOB= °.
(2)若∠AOB=α,∠BOC=β(其中α<β<90°),画出图形并直接写出∠MOB的度数.(用含α,β的式子表示)
28.(2022·北京四中璞瑅学校七年级期中)如图,在一片农田附近有一条小河.因为干旱,附近的农民们常常需要从河中引水灌溉农田.张伯伯家的农田位于图中点处,他也想挖一条水渠,把河水引到自家农田处.
(1)请问,张伯伯如何挖渠才能使渠道最短?请你在如图中画出来.
(2)你这样画的依据是什么?
(3)如果图中比例尺为:,水渠大概要挖多长?
(4)请你举出一个生活中应用以上“依据”的实际例子.
29.(2022·北京密云·七年级期末)如图,直线,E为直线CD上一点,射线EH交直线AB于点F.
(1)按要求画图:
①利用量角器及直尺,画∠FED的角平分线EM,交直线AB于点N;
②过点N作NP⊥CD,垂足为P.
(2)完成下列填空:
比较线段NE和NP的大小,可以得到NE____________NP;(填“>”、“=”或“<”)理由是____________.
30.(2022·北京·七年级期中)如图,点A在的一边上.按下列要求画图:
(1)过点A画直线,与的另一边相交于点B;
(2)过点A画的垂线段,垂足为点C;
(3)过点C画直线∥,交直线于点D;
参考答案:
1.B
【解析】根据题意,直径为60厘米,在生活中可能是井盖的面的大小,据此解答即可.
解:杯盖的面、一元硬币的面都小于直径60厘米的圆,蒙古包的占地面积大于直径60厘米的圆,只有井盖的面接近直径60厘米的圆.
故选:B.
【点睛】此题考查了认识平面图形,要注意联系实际,计量单位和数据的大小,灵活选择.
2.C
【解析】根据每一个几何体的特征即可判断.
解:A是圆柱体;
B是正方体;
C是圆锥;
D是四棱锥;
故选:C
【点睛】本题考查了认识立体图形,熟练掌握每一个几何体的特征是解题的关键.
3.D
【解析】通过空间想象,将展开图还原成立体图,再去推测每个面及其对面的汉字是什么.
折叠后:“一”和 “向”相对;
“起”和“来”相对;
“走”和“未”相对;
故A、B、C均不对;D对,符合题意;
故选D
【点睛】本题考查正方体相对两面上字,展开空间想象找到每个字对面的字是关键.
4.C
【解析】逐一分析从正面看到的图形即可解题.
A.从正面看是长方形,故A不符合题意;
B. 从正面看是长方形形,故B不符合题意;
C. 从正面看是是三角形,故C符合题意;
D. 从正面看是两个长方形拼成的几何图形,故D不符合题意.
故选:C.
【点睛】本题考查从正面看几何体,是基础考点,掌握相关知识是解题关键.
5.C
【解析】根据数的分类、钝角的定义、倍数的性质和含盐率公式逐一判断即可.
解:A. 一个数除了正数和负数外,还有可能是0,故本选项错误;
B. 大于且小于180°的角都是钝角,缺少条件,故本选项错误;
C. 是6的倍数的数也一定是3的倍数,故本选项正确;
D. 5千克盐溶解在100千克水中,盐水的含盐率是5÷(100+5)≈%,故本选项错误.
故选C.
【点睛】此题考查的是数的分类、钝角的定义、倍数的性质和求含盐率,掌握数的分类、钝角的定义、倍数的性质和含盐率公式是解决此题的关键.
6.C
【解析】根据题意得:∠ADB=45°,∠BDC=90°,从而得到∠ADC=∠ADB+∠BDC=135°,即可求解.
解:根据题意得:∠ADB=45°,∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
故选:C
【点睛】本题主要考查了直角三角板中角的计算,熟练掌握一副直角三角板中每个角的度数是解题的关键.
7.C
【解析】根据角平分线的定义可得∠AOD=2∠EOD,∠BOD=2∠DOF,结合平角的定义可求解∠EOF=90°,由∠EOF的度数为定值可判定求解.
解:∵OE平分∠AOD,OF平分∠BOD,
∴∠AOD=2∠EOD,∠BOD=2∠DOF,
∵∠AOD+∠BOD=180°,
∴∠EOD+∠DOF=90°,
即∠EOF=90°,
∴直线CD绕点O顺时针旋转α°(0<α<180)时,∠EOF的度数与∠BOD度数变化无关.
故选:C.
【点睛】本题主要考查角平分线的定义,求解∠EOF的度数是解题的关键.
8.B
【解析】首先弄清各图中,∠1,∠2是哪两条直线被另一条直线所截形成的角;接下来根据互为同旁内角的两角的位置特点,进行判别即可.
解:A.∠1,∠2在截线的同旁,在两条被截线同方向,是同位角,故选项A不合题意;
B.∠1,∠2在截线的同旁,夹在两条被截线同旁是同旁内角,故选项B符合题意;
C.∠1,∠2不是两条直线被第三条直线在截线的角,不是同位角,内错角,同旁内角,故选项C不合题意;
D.∠1,∠2截线两侧,在两被截直线的外部形成的角,所以不是同旁内角(也不是同位角,更不是内错角)故选项D不合题意.
故选B.
【点睛】本题考查了同位角、同旁内角、内错角,熟悉掌握定义是解题关键.
9.A
【解析】利用垂线段最短的原理即可判断.
解:从人行横道线上的点P处过马路,沿线路PB行走且,所以由垂线段最短的原理可以知,沿线路PB行走距离最短,
故选:A.
【点睛】本题考查了垂线段最短的原理,解题的关键是:掌握垂线段最短的原理.
10.B
【解析】根据题意抽象为过直线外一点到直线的距离最短分析即可
根据题意,小河可以抽象为一条直线,点到直线的所有连线中,垂线段最短
理由是: 垂线段最短
故选B
【点睛】本题考查了垂线段最短的应用,理解题意是解题的关键.
11.A
【解析】根据点到直线的距离、平面内两直线的位置关系求解即可.
量出直线外一点到直线的垂线段的长度即为点到直线的距离,
故正确;
在同一平面内,两条不同直线有一个公共点或没有公共点,
故错误;
从直线外一点到这条直线的垂线段的长度叫作点到直线的距离,
故错误;
同一平面内两条直线有相交、平行两种位置关系,
故错误;
故选:.
【点睛】此题考查了平面内两直线的位置关系、点到直线的距离,熟练掌握平面内两直线的位置关系、点到直线的距离是解题的关键.
12.C
【解析】过E作EF∥AB CD,由平行线的质可得∠1=∠3,∠2=∠4, ∠3+∠4=∠1+∠2,根据三角形内角和可得: ∠3+∠4=60°,从而可得: ∠1+∠2=60°,由∠1=20°,可得: ∠2=40°.
如图,过E作EF∥AB,
则AB∥EF∥CD,
∴∠1=∠3,∠2=∠4,
∵∠3+∠4=60°,
∴∠1+∠2=60°,
∵∠1=20°,
∴∠2=40°,
故选C.
【点睛】本题考查了平行线的性质,解决本题的关键是要正确作出辅助线和熟练掌握平行线的性质.
13.②⑤
【解析】结合题意,根据简单几何体展开图的性质对各个选项逐个分析,即可得到答案.
根据题意,再剪开一条棱,展开图不可能为:
故答案为:②⑤.
【点睛】本题考查了几何体展开图的知识;解题的关键是熟练掌握简单几何体展开图的性质,从而完成求解.
14.2或4##4或2
【解析】分点C在线段AB上和点C在线段AB的延长线上两种情况考虑,利用中点及线段和差关系即可求得AD的长度.
当点C在线段AB上时,如图:
∵AB=6cm,BC=2cm
∴AC=AB-BC=6-2=4(cm)
∵D是线段AC的中点
∴
当点C在线段AB的延长线上时,如图:
∵AC=AB+BC=6+2=8(cm)
∵D是线段AC的中点
∴
故答案为:2或4
【点睛】本题考查了中点的意义及线段的和差关系,涉及分类讨论.
15.3.6
【解析】首先设AC=2xcm,则线段CD=3xcm,DB=4xcm,然后根据E、F分别是线段AC、DB的中点,分别用x表示出EC、DF,根据EF=2.4cm,求出x的值,即可求出线段AB的长是多少.
设AC=2x,则线段CD=3x,DB=4x,
∵E、F分别是线段AC、DB的中点,
∴EC=AC=x,DF=DB=2x,
∵EF=EC+CD+DF=x+3x+2x=2.4,
∴x=0.4,
∴AB=9x=9×0.4=3.6(cm),
故答案为:3.6.
【点睛】此题主要考查了两点间的距离的求法,以及线段的中点的特征和应用,要熟练掌握.
16. 42 同角的余角相等
【解析】由同角的余角相等可得∠2=∠1=42°.
解:如图,
∵将两块三角板的直角顶点重合后叠放在一起,
∴∠1+∠3=∠2+∠3=90°,
∴∠2和∠1都是∠3的余角,
∴∠2=∠1=42°,
故答案为:42,同角或等角的余角相等.
【点睛】本题考查了同角或等角的余角相等,看懂图形是解题的关键.
17.53
【解析】根据图形,利用量角器直接测量即可.
如图,经用量角器测量得到∠ABO=53°
故答案为:53.
【点睛】本题考查方位角和角的测量,是基础题.
18.
【解析】由角的三等分线的含义先求解 再结合角的三等分线可得从而可得答案.
解: ,OB是的三等分线,
OC分别是的三等分线,
故答案为:
【点睛】本题考查的是角的三等分线的应用,结合角的和差关系理解图形中的三等分线是解本题的关键.
19.30°
因∠1和∠2是邻补角,且∠1=30°,由邻补角的定义可得∠2=180°﹣∠1=180°﹣30°=150°.
解:∵∠1+∠2=180°,
又∠1=30°,
∴∠2=150°.
20. 垂线段最短 AB
【解析】根据垂线段最短即可求解.
解:∵AC⊥BC,
∴AC<AB,BC<AB,
∴AB最长.
即在AC,BC,AB三边中,根据垂线段最短,可知AB最长.
故答案为:垂线段最短,AB.
【点睛】本题考查了垂线的性质,掌握垂线段最短是解题的关键.
21.3
【解析】点到直线的距离是指过直线外一点向直线做的垂线段的长度,根据定义可以得出答案.
解:∵,
∴AC⊥BC,
∴线段AC的长度就是点A到BC的距离,
∵AC=3,
∴点A到的距离等于3.
故答案为:3.
【点睛】本题主要考查的是点到直线的距离,属于基础题型.解决这个问题的关键就是要明白点到直线距离的定义.
22.75
【解析】首先计算的度数,再根据平行线的性质可得,进而可得答案.
解:∵,,
∴,
∵,
∴,
故答案为:75.
【点睛】此题主要考查了平行线的性质,掌握平行线的性质并能灵活应用是解题关键.
23.(1)见解析
(2)见解析
【解析】(1)让直尺的边沿同时过A,B两点,画直线即可;
(2)分点D在点B的右侧和左侧两种情形画图.
(1)
画图如下:
(2)
画图如下:
【点睛】本题考查了直线,射线,线段的基本画图,正确使用直尺,灵活进行分类是解题的关键.
24.1或5
【解析】根据题意,分两种情况:(1)点D在点B的右侧时,(2)点D在点B的左侧时,求出线段DC的长度是多少即可.
解:
∵点C是AB的中点,
∴.
∵AB=6,
当点D在点B左侧时;
∵DB=2,
∴
当点D在点B右侧时;
.
【点睛】本题考查了利用中点性质转化线段之间倍分关系,从而求出线段的长短.解题的关键是在不同情况下灵活运用它的不同表示方法,同时灵活运用线段的和差倍分转化线段之间的数量关系也是十分关键的一点.
25.见解析
【解析】利用方向角分别得出北偏东45°方向以及北偏西60°方向的位置产生的交点即为所求.
解:如图所示:先作北偏东45°方向的射线AO,然后作北偏西60°方向的射线BO,两条射线交于点O,点O即为这艘船的位置.
【点睛】此题主要考查了应用设计与作图,正确掌握方向角的确定方法是解题关键.
26.(1)画图见解析,基本事实:两点确定一条直线;(2)画图见解析;(3)画图见解析;(4)画图见解析;(5)
【解析】(1)直接过AB两点画直线即可;
(2)用量角器直接画图即可;
(3)以B为圆心,BA长度为半径画圆即可;
(4)用带刻度的直尺量出AD长度取中点即可;
(5)用量角器测量各个角度大小即可;
(1)画图如下,基本事实:两点确定一条直线
(2)画图如下;
(3)画图如下;
(4)画图如下;
(5)不唯一,正确即可.
例如:,,等
或
【点睛】本题考查线段和角度作图,熟练使用量角器、圆规和带刻度的直尺是解题的关键.
27.(1)①见解析;②,45,∠COB,75
(2)见解析,或
【解析】(1)①根据题意作图即可;
②利用角平分线计算得,再结合图形计算即可得;
(2)分两种情况讨论,如解析中图象所示,分别利用角平分线进行计算即可得.
(1)
①根据题意,作图如下:
②解:∵,,,
∴.
∵OM平分,
∴,
∵,
∴;
故答案为:;;;;
(2)
解:分两种情况讨论:
①如图所示:,,
∴,
∴,
∴;
②如图所示:,,
∴,
∴,
∴;
综上可得:或.
【点睛】题目主要考查角平分线的计算,理解题意,充分利用角平分线进行计算是解题关键.
28.(1)见解析;
(2)垂线段最短;
(3)水渠大概要挖米;
(4)体育课上测量跳远成绩的依据也是利用垂线段最短.
【解析】(1)作PH⊥CD即可;
(2)根据垂线段最短解决问题;
(3)测量出PH的长,再利用比例尺求出实际距离;
(4)体育课上测量跳远成绩的依据也是利用垂线段最短.
(1)
解:如图,作,线段即为所求;
(2)
解:画图的依据是垂线段最短.
(3)
解: ,
∴实际距离为m,
水渠大概要挖m;
(4)
解:体育课上测量跳远成绩的依据也是利用垂线段最短.
【点睛】本题考查作图—应用与设计作图,垂线段最短,比例尺等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
29.(1)见解析
(2)>;垂线段最短
【解析】(1)①利用量角器及直尺可直接进行作图;②根据垂线可进行作图;
(2)根据垂线段最短可进行求解.
(1)
解:如图所示:
(2)
解:比较线段NE和NP的大小,可以得到NE>NP;理由是垂线段最短;
故答案为>,垂线段最短.
【点睛】本题主要考查尺规作图及垂线段最短,熟练掌握垂线的作图及垂线段最短是解题的关键.
30.(1)见解析
(2)见解析
(3)见解析
【解析】(1)根据垂线的定义作图即可;
(2)根据垂线段的定义作图即可;
(3)根据平行线的定义作图即可.
(1)
如图,直线AB即为所求.
(2)
如图,垂线段即为所求.
(3)
如图,直线CD即为所求.
【点睛】本题考查了作图,涉及垂线、垂线段及平行线,熟练掌握知识点是解题的关键.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
