人教A版(2019)高中数学必修第二册 《统计》章末综合测评(word含解析)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《统计》章末综合测评(word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 810.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览




文档简介
本章综合测评
一、单项选择题
1.某公司从代理的A,B,C,D四种产品中,按分层随机抽样的方法抽取容量为110的样本,已知A,B,C,D四种产品的数量比是2:3:2:4,则该样本中D类产品的数量为( )
A.22
B.33
C.40
D.55
2.下列抽样方式是简单随机抽样的是( )
A.某工厂从老年、中年、青年职工中按2:5:3的比例选取职工代表
B.从平面直角坐标系中抽取5个点作为样本
C.福利彩票用摇奖机摇奖
D.规定凡买到明信片最后的几位号码是“6637”的人获三等奖
3.某市电视台为调查节目收视率,想从全市三个区按人口数用分层随机抽样的方法抽取一个容量为n的样本,已知三个区人口数之比为2:3:5,如果人口最多的一个区抽出60人,那么n等于( )
A.96
B.120
C.180
D.240
4.若数据的平均数为,方差为,则的平均数和标准差分别为( )
A.
B.
C.
D.
5.如图为某个容量为100的样本的频率分布直方图,分组为,,,,,则在区间上的数据的频数为( )
A.0.1
B.0.2
C.20
D.10
6.2019年某学科能力测试共有12万考生参加,成绩采用15级分,测试成绩分布图如图,试估计成绩高于11级分的人数为( )
A.8000
B.10000
C.20000
D.60000
7.在抽取样本时,用频率分布直方图表示尺寸的过程中,将其尺寸分成若干组,是其中的组,抽查出的个数在该组上的频率为m,该组上的小矩形的高为h,则等于( )
A.
B.
C.
D.
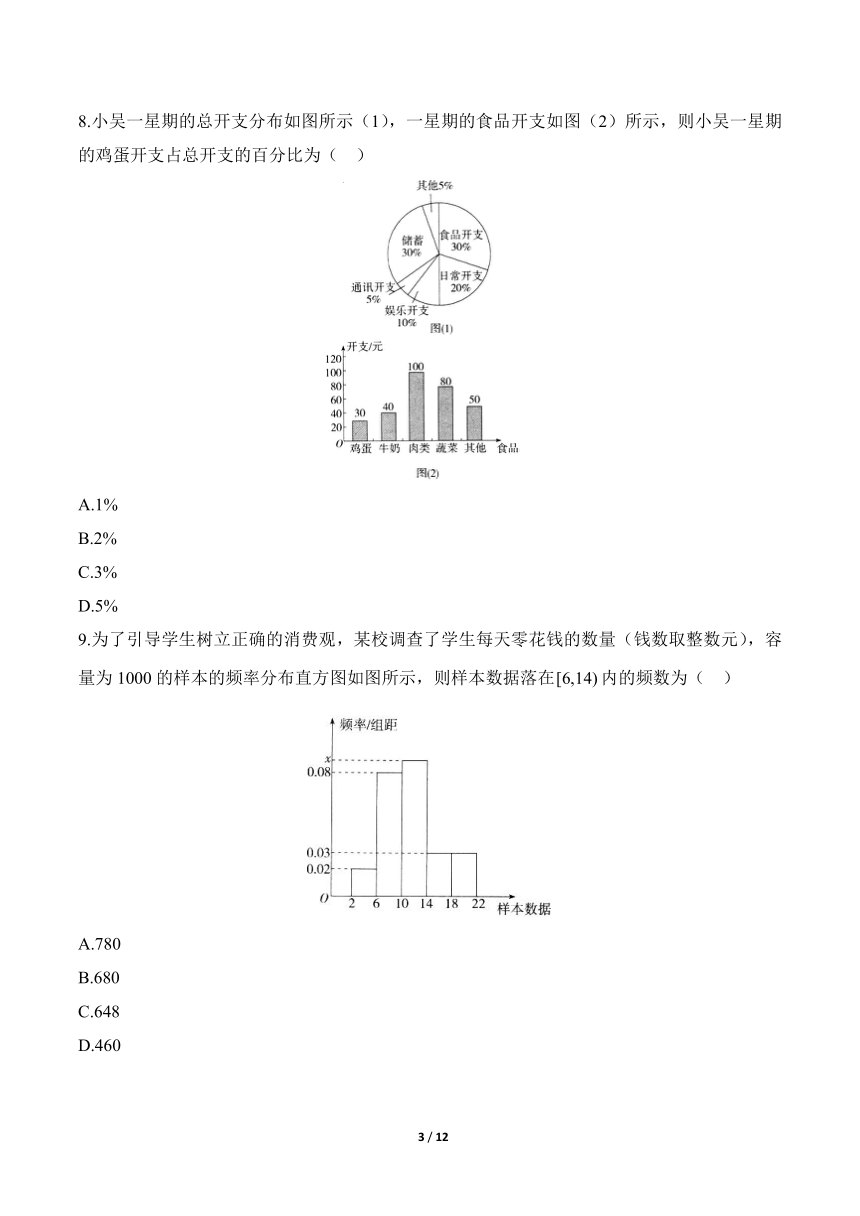
8.小吴一星期的总开支分布如图所示(1),一星期的食品开支如图(2)所示,则小吴一星期的鸡蛋开支占总开支的百分比为( )
A.1%
B.2%
C.3%
D.5%
9.为了引导学生树立正确的消费观,某校调查了学生每天零花钱的数量(钱数取整数元),容量为1000的样本的频率分布直方图如图所示,则样本数据落在内的频数为( )
A.780
B.680
C.648
D.460
二、多项选择题
10.下列关于抽样的说法中正确的是( )
A.已知总体容量为109,若要用随机数法抽取一个容量为10的样本,可以将总体编号为000,001,002,003,…,108
B.当总体、样本容量较大时,一般采用简单随机抽样
C.当总体由有明显差异的几部分构成时,可以采用分层随机抽样
D.总体容量较大且总体中的个体无明显差异,宜采用随机数法
11.关于统计数据的分析,有以下几个结论,其中错误的是( )
A.一组数据不可能有两个众数
B.将一组数据中的每个数据都减去同一个数后,方差没有变化
C.一组数据的方差一定是正数
D.一组数据的方差是,将这组数据中的每一个数都乘2,得到一组新数据的方差是
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是连续7天每天新增感染人数不超过5”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.标准差
B.平均数,且标准差
C.平均数,且极差小于或等于2
D.众数等于1,且极差小于或等于4
三、填空题
13.某学院的A,B,C三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层随机抽样的方法抽取一个容量为120的样本.已知该学院的A专业有380名学生,B专业有420名学生,则在该学院的C专业应抽取_____名学生.
14. 某校在一次学生演讲比赛中,共有7个评委,若学生最后得分为去掉一个最高分和一个最低分的平均分.若某学生所得分数为9.6,9.4,9.6,9.7,9.7,9.5,9.6,则这组数据的众数是_____,该学生最后得分为_____.
15.已知样本数据的均值,则样本数据,,…,的均值为_____.
16.为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位千克)全部介于45至70之间将数据分成以下5组:第1组,第2组,第3组,第4组,第5组,得到如图所示的频率分布直方图,则_____.
现采用分层随机抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次为_____.
四、解答题
17.有以下两个案例:
案例一:从同一批次同一型号的10袋牛奶中抽取3袋检测其三聚氰胺含量;
案例二:某公司有员工800人,其中具有高级职称的有160人,具有中级职称的有320人,具有初级职称的有200人,其余人员有120人从中抽取容量为40的样本,了解该公司职工收入情况.
(1)你认为这些案例应采用怎样的抽样方式较为合适?
(2)在你使用的分层随机抽样案例中写出抽样过程.
18.一箱方便面共有50袋,用简单随机抽样的方法从中抽取了10袋,并称其质量(单位:g)结果为60.5,61,60,60,61.5,59.559.5,58.60,60.
(1)指出总体个体、样本、样本容量;
(2)指出样本数据的众数、中位数、平均数;
(3)求样本数据的方差.
19.农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下(单位:cm):
甲:9,10,11,12,10,20;
乙:8,14,13,10,12,21分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
20. 2018年10月24日上午9时港珠澳大桥正式通车,这座被誉为“新世界七大奇迹”的大桥,问鼎多项“世界之最”:世界上总体跨度最长、钢结构桥体最长、海底沉管隧道最长的跨海大桥;是公路建设史上技术最复杂、施工难度最高、工程规模最庞大的桥梁,世界最大尺寸高阻尼橡胶隔震支座、世界最大难度深水无人对接的沉管隧道等等现在在某市中学生中,对这座世纪大桥的了解程度进行调查,随机选取了100人进行问卷调查,并将问卷中的这100人根据其了解度评分值(百分制)按照,,…,分成5组,制成如图所示的频率分布直方图.
(1)求图中x的值;
(2)求这组数据的平均数和中位数.
21.为选派一名学生参加全市实践活动技能竞赛,A、B两位同学在学校学习基地现场进行加工直径为20mm的零件的测试,他们各加工的10个零件(单位:mm)的相关数据如下面的图表所示.
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,说明谁的成绩好些;
(2)计算出的大小,考虑平均数与方差,说明谁的成绩好些;
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.
22.某学校为了解学校餐厅的服务情况,随机调查了50名前来就餐的教师和学生根据这50名师生对餐厅服务质量的评分,绘制出了如图所示的频率分布直方图,其中样本数据分组为,,…,[90,100].
(1)求频率分布直方图中a的值;
(2)若采用分层随机抽样的方式从评分在,,的师生中抽取10人,则应从评分在的师生中抽取多少人?
(3)学校规定:师生对餐厅服务质量的评分不得低于75分,否则将进行内部整顿用每组数据的中点值代替该组数据,试估计该校师生对餐厅服务质量评分的平均分,并据此回答餐厅是否需要进行内部整顿.
参考答案
一、单项选择题
1.
答案:C
解析:根据分层随机抽样,知总体中产品数量比与抽取的样本中产品数量比相等,样本中D类产品的数量为.
2.
答案:C
解析:简单随机抽样要求总体中的个体数有限,从总体中逐个进行抽样,每个个体有相同的可能性被抽到根据简单随机抽样的上述特点可知,只有选项C符合.
3.
答案:B
解析:由三个区人口数之比为2:3:5,得第三个区所抽取的人口数最多,所占比例为50%又因为此区抽取60人,所以三个区所抽取的总人口数为,即n等于120.
4.
答案:C
解析:的平均数为,
的平均数为,
.
5.
答案:C
解析:由频率分布直方图可知频数为.
6.
答案:B
解析:从题图中可以看出,12级分的有5%左右,13级分的有3%左右,14级分的有1%左右,15级分的有1.5%左右,高于11级分的有8%左右,其人数约为12万的8%,即人.选项B最接近.故选B.
7.
答案:C
解析:是组距,在频率分布直方图中,组距是该组上的小矩形的高h,
即,.
8.
答案:C
解析:由题图(1)可知,食品开支占总开支的30%,由题图(2)可知,鸡蛋开支占食品开支的,鸡蛋开支占总开支的百分比为.
9.
答案:B
解析:依题意知,故.数据落在内的频率为,因此频数为.故选B.
二、多项选择题
10.
答案:ACD
解析:注意两种抽样的不同之处,以及它们所适用的范围.
11.
答案:AC
解析:一组数据中可以有多个众数,故结论A错误;根据方差的计算方法可知结论B正确;方差可以是零,故结论C错误;由方差的性质可知新数据的方差是4s2,故结论D正确.
12.
答案:CD
解析:标准差控制个体稳定性,不能控制个体水平,如七天都为6人,标准差为零,满足A,但不符合指标B、C、D都从两个方面进行控制,要符合指标,必须分析控制的量是否达标如:七天数据为3,3,3,3,1,2,6则平均数,且,满足B,但不符合指标若极差等于0或1,在的条件下显然符合指标,若极差等于2,则有下列可能:
(1)0,1,2,(2)1,2,3,(3)2,3,4,(4)3,4,5,(5)4,5,6.在的条件下,只有(1)(2)(3)成立,C符合指标若众数等于1,且极差小于或等于4,则最大数不超过5,D符合指标故选CD.三、填空题
13.
答案:40
解析:由题知C专业有学生(名),那么C专业应抽取的学生数为.
14.
答案:9.6;9.6
解析:根据题意,得这组数据的众数为9.6,平均分为,故最后得分为9.6.
15.
答案:11
解析:因为样本数据的均值,所以样本数据,,…,的均值为.
16.
答案:0.04;3,2,1
解析:由,得.
设第3,4,5组抽取的学生人数依次为,
则,
又,所以,,.
四、解答题
17.
答案:见解析
解析:(1)案例一采用简单随机抽样,案例二采用分层随机抽样.
(2)抽样过程如下:①分层,将总体分为高级职称、中级职称、初级职称及其余人员四层;
②确定抽样比标例;
③按上述比例确定各层样本量分别为8、16、10、6;
④用简单随机抽样的方法在各层确定相应的样本;
⑤汇总构成一个容量为40的样本.
18.
答案:见解析
解析:(1)总体是这50袋方便面的质量,个体是这一箱方便面中每一袋方便面的质量,样本是抽取的10袋方便面的质量,样本容量为10.
(2)这组样本数据的众数是60,中位数是60,平均数.
(3)样本数据的方差
.
19.
答案:见解析
解析:,,
方差,
EMBED Equation.DSMT4 .
因为,所以乙种麦苗平均株高较高;
因为,所以甲种麦苗长的较为整齐.
20.
答案:见解析
解析:(1)由,解得.
(2)这组数据的平均数为.
设中位数为m,则解得.
21.
答案:见解析
解析:(1)因为A、B两位同学成绩的平均数相同,B同学加工的零件中完全符合要求的个数较多,所以B同学的成绩好些.
(2)因为,
且,所以,在平均数相同的情况下,B同学加工零件的直径波动小,所以B同学的成绩好些.
(3)选派A同学去参赛较合适从题干图中折线走势可知,尽管A同学的成绩前面起伏大,但后来逐渐稳定,误差小,预测A同学的潜力大,而B同学比较稳定,潜力小,所以选派A同学去参赛较适.
22.
答案:见解析
解析:(1)由,解得.
(2)由频率分布直方图可知,评分在
,,的师生人数之比为,所以评分在的师生中应抽取(人).
(3)服务质量评分的平均分为
. ,餐厅不需要内部整顿.
1 / 12
一、单项选择题
1.某公司从代理的A,B,C,D四种产品中,按分层随机抽样的方法抽取容量为110的样本,已知A,B,C,D四种产品的数量比是2:3:2:4,则该样本中D类产品的数量为( )
A.22
B.33
C.40
D.55
2.下列抽样方式是简单随机抽样的是( )
A.某工厂从老年、中年、青年职工中按2:5:3的比例选取职工代表
B.从平面直角坐标系中抽取5个点作为样本
C.福利彩票用摇奖机摇奖
D.规定凡买到明信片最后的几位号码是“6637”的人获三等奖
3.某市电视台为调查节目收视率,想从全市三个区按人口数用分层随机抽样的方法抽取一个容量为n的样本,已知三个区人口数之比为2:3:5,如果人口最多的一个区抽出60人,那么n等于( )
A.96
B.120
C.180
D.240
4.若数据的平均数为,方差为,则的平均数和标准差分别为( )
A.
B.
C.
D.
5.如图为某个容量为100的样本的频率分布直方图,分组为,,,,,则在区间上的数据的频数为( )
A.0.1
B.0.2
C.20
D.10
6.2019年某学科能力测试共有12万考生参加,成绩采用15级分,测试成绩分布图如图,试估计成绩高于11级分的人数为( )
A.8000
B.10000
C.20000
D.60000
7.在抽取样本时,用频率分布直方图表示尺寸的过程中,将其尺寸分成若干组,是其中的组,抽查出的个数在该组上的频率为m,该组上的小矩形的高为h,则等于( )
A.
B.
C.
D.
8.小吴一星期的总开支分布如图所示(1),一星期的食品开支如图(2)所示,则小吴一星期的鸡蛋开支占总开支的百分比为( )
A.1%
B.2%
C.3%
D.5%
9.为了引导学生树立正确的消费观,某校调查了学生每天零花钱的数量(钱数取整数元),容量为1000的样本的频率分布直方图如图所示,则样本数据落在内的频数为( )
A.780
B.680
C.648
D.460
二、多项选择题
10.下列关于抽样的说法中正确的是( )
A.已知总体容量为109,若要用随机数法抽取一个容量为10的样本,可以将总体编号为000,001,002,003,…,108
B.当总体、样本容量较大时,一般采用简单随机抽样
C.当总体由有明显差异的几部分构成时,可以采用分层随机抽样
D.总体容量较大且总体中的个体无明显差异,宜采用随机数法
11.关于统计数据的分析,有以下几个结论,其中错误的是( )
A.一组数据不可能有两个众数
B.将一组数据中的每个数据都减去同一个数后,方差没有变化
C.一组数据的方差一定是正数
D.一组数据的方差是,将这组数据中的每一个数都乘2,得到一组新数据的方差是
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是连续7天每天新增感染人数不超过5”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.标准差
B.平均数,且标准差
C.平均数,且极差小于或等于2
D.众数等于1,且极差小于或等于4
三、填空题
13.某学院的A,B,C三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层随机抽样的方法抽取一个容量为120的样本.已知该学院的A专业有380名学生,B专业有420名学生,则在该学院的C专业应抽取_____名学生.
14. 某校在一次学生演讲比赛中,共有7个评委,若学生最后得分为去掉一个最高分和一个最低分的平均分.若某学生所得分数为9.6,9.4,9.6,9.7,9.7,9.5,9.6,则这组数据的众数是_____,该学生最后得分为_____.
15.已知样本数据的均值,则样本数据,,…,的均值为_____.
16.为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位千克)全部介于45至70之间将数据分成以下5组:第1组,第2组,第3组,第4组,第5组,得到如图所示的频率分布直方图,则_____.
现采用分层随机抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次为_____.
四、解答题
17.有以下两个案例:
案例一:从同一批次同一型号的10袋牛奶中抽取3袋检测其三聚氰胺含量;
案例二:某公司有员工800人,其中具有高级职称的有160人,具有中级职称的有320人,具有初级职称的有200人,其余人员有120人从中抽取容量为40的样本,了解该公司职工收入情况.
(1)你认为这些案例应采用怎样的抽样方式较为合适?
(2)在你使用的分层随机抽样案例中写出抽样过程.
18.一箱方便面共有50袋,用简单随机抽样的方法从中抽取了10袋,并称其质量(单位:g)结果为60.5,61,60,60,61.5,59.559.5,58.60,60.
(1)指出总体个体、样本、样本容量;
(2)指出样本数据的众数、中位数、平均数;
(3)求样本数据的方差.
19.农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下(单位:cm):
甲:9,10,11,12,10,20;
乙:8,14,13,10,12,21分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
20. 2018年10月24日上午9时港珠澳大桥正式通车,这座被誉为“新世界七大奇迹”的大桥,问鼎多项“世界之最”:世界上总体跨度最长、钢结构桥体最长、海底沉管隧道最长的跨海大桥;是公路建设史上技术最复杂、施工难度最高、工程规模最庞大的桥梁,世界最大尺寸高阻尼橡胶隔震支座、世界最大难度深水无人对接的沉管隧道等等现在在某市中学生中,对这座世纪大桥的了解程度进行调查,随机选取了100人进行问卷调查,并将问卷中的这100人根据其了解度评分值(百分制)按照,,…,分成5组,制成如图所示的频率分布直方图.
(1)求图中x的值;
(2)求这组数据的平均数和中位数.
21.为选派一名学生参加全市实践活动技能竞赛,A、B两位同学在学校学习基地现场进行加工直径为20mm的零件的测试,他们各加工的10个零件(单位:mm)的相关数据如下面的图表所示.
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,说明谁的成绩好些;
(2)计算出的大小,考虑平均数与方差,说明谁的成绩好些;
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.
22.某学校为了解学校餐厅的服务情况,随机调查了50名前来就餐的教师和学生根据这50名师生对餐厅服务质量的评分,绘制出了如图所示的频率分布直方图,其中样本数据分组为,,…,[90,100].
(1)求频率分布直方图中a的值;
(2)若采用分层随机抽样的方式从评分在,,的师生中抽取10人,则应从评分在的师生中抽取多少人?
(3)学校规定:师生对餐厅服务质量的评分不得低于75分,否则将进行内部整顿用每组数据的中点值代替该组数据,试估计该校师生对餐厅服务质量评分的平均分,并据此回答餐厅是否需要进行内部整顿.
参考答案
一、单项选择题
1.
答案:C
解析:根据分层随机抽样,知总体中产品数量比与抽取的样本中产品数量比相等,样本中D类产品的数量为.
2.
答案:C
解析:简单随机抽样要求总体中的个体数有限,从总体中逐个进行抽样,每个个体有相同的可能性被抽到根据简单随机抽样的上述特点可知,只有选项C符合.
3.
答案:B
解析:由三个区人口数之比为2:3:5,得第三个区所抽取的人口数最多,所占比例为50%又因为此区抽取60人,所以三个区所抽取的总人口数为,即n等于120.
4.
答案:C
解析:的平均数为,
的平均数为,
.
5.
答案:C
解析:由频率分布直方图可知频数为.
6.
答案:B
解析:从题图中可以看出,12级分的有5%左右,13级分的有3%左右,14级分的有1%左右,15级分的有1.5%左右,高于11级分的有8%左右,其人数约为12万的8%,即人.选项B最接近.故选B.
7.
答案:C
解析:是组距,在频率分布直方图中,组距是该组上的小矩形的高h,
即,.
8.
答案:C
解析:由题图(1)可知,食品开支占总开支的30%,由题图(2)可知,鸡蛋开支占食品开支的,鸡蛋开支占总开支的百分比为.
9.
答案:B
解析:依题意知,故.数据落在内的频率为,因此频数为.故选B.
二、多项选择题
10.
答案:ACD
解析:注意两种抽样的不同之处,以及它们所适用的范围.
11.
答案:AC
解析:一组数据中可以有多个众数,故结论A错误;根据方差的计算方法可知结论B正确;方差可以是零,故结论C错误;由方差的性质可知新数据的方差是4s2,故结论D正确.
12.
答案:CD
解析:标准差控制个体稳定性,不能控制个体水平,如七天都为6人,标准差为零,满足A,但不符合指标B、C、D都从两个方面进行控制,要符合指标,必须分析控制的量是否达标如:七天数据为3,3,3,3,1,2,6则平均数,且,满足B,但不符合指标若极差等于0或1,在的条件下显然符合指标,若极差等于2,则有下列可能:
(1)0,1,2,(2)1,2,3,(3)2,3,4,(4)3,4,5,(5)4,5,6.在的条件下,只有(1)(2)(3)成立,C符合指标若众数等于1,且极差小于或等于4,则最大数不超过5,D符合指标故选CD.三、填空题
13.
答案:40
解析:由题知C专业有学生(名),那么C专业应抽取的学生数为.
14.
答案:9.6;9.6
解析:根据题意,得这组数据的众数为9.6,平均分为,故最后得分为9.6.
15.
答案:11
解析:因为样本数据的均值,所以样本数据,,…,的均值为.
16.
答案:0.04;3,2,1
解析:由,得.
设第3,4,5组抽取的学生人数依次为,
则,
又,所以,,.
四、解答题
17.
答案:见解析
解析:(1)案例一采用简单随机抽样,案例二采用分层随机抽样.
(2)抽样过程如下:①分层,将总体分为高级职称、中级职称、初级职称及其余人员四层;
②确定抽样比标例;
③按上述比例确定各层样本量分别为8、16、10、6;
④用简单随机抽样的方法在各层确定相应的样本;
⑤汇总构成一个容量为40的样本.
18.
答案:见解析
解析:(1)总体是这50袋方便面的质量,个体是这一箱方便面中每一袋方便面的质量,样本是抽取的10袋方便面的质量,样本容量为10.
(2)这组样本数据的众数是60,中位数是60,平均数.
(3)样本数据的方差
.
19.
答案:见解析
解析:,,
方差,
EMBED Equation.DSMT4 .
因为,所以乙种麦苗平均株高较高;
因为,所以甲种麦苗长的较为整齐.
20.
答案:见解析
解析:(1)由,解得.
(2)这组数据的平均数为.
设中位数为m,则解得.
21.
答案:见解析
解析:(1)因为A、B两位同学成绩的平均数相同,B同学加工的零件中完全符合要求的个数较多,所以B同学的成绩好些.
(2)因为,
且,所以,在平均数相同的情况下,B同学加工零件的直径波动小,所以B同学的成绩好些.
(3)选派A同学去参赛较合适从题干图中折线走势可知,尽管A同学的成绩前面起伏大,但后来逐渐稳定,误差小,预测A同学的潜力大,而B同学比较稳定,潜力小,所以选派A同学去参赛较适.
22.
答案:见解析
解析:(1)由,解得.
(2)由频率分布直方图可知,评分在
,,的师生人数之比为,所以评分在的师生中应抽取(人).
(3)服务质量评分的平均分为
. ,餐厅不需要内部整顿.
1 / 12
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
