人教A版(2019)高中数学必修第二册 《统计》单元测试(二)(word含解析)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《统计》单元测试(二)(word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 858.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览


文档简介
《统计》单元测试(二)
一、选择题
1.下列抽样方法是简单随机抽样的是( )
A.从100个学生家长中一次性随机抽取10人做家访
B.从38本教辅参考资料中一次性随机抽取3本作为教学参考
C.从自然数集中一次性抽取20个进行奇偶性分析
D.某参会人员从最后一排20个座位中随机选择一个坐下
2.从800件产品中抽取60件进行质检,利用随机数法抽取样本时,先将800件产品按001,002,…,800进行编号,利用计算机随机产生如下0~9的随机数,现从第2行第8列的数8开始往右读数(三位三位地读),则抽取的第4件产品的编号是( )
A.169
B.556
C.671
D.105
3.某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,统计结果如下图所示.已知9时至10时的销售额为3万元,则9时至14时的销售总额为( )
A.10万元
B.12万元
C.15万元
D.30万元
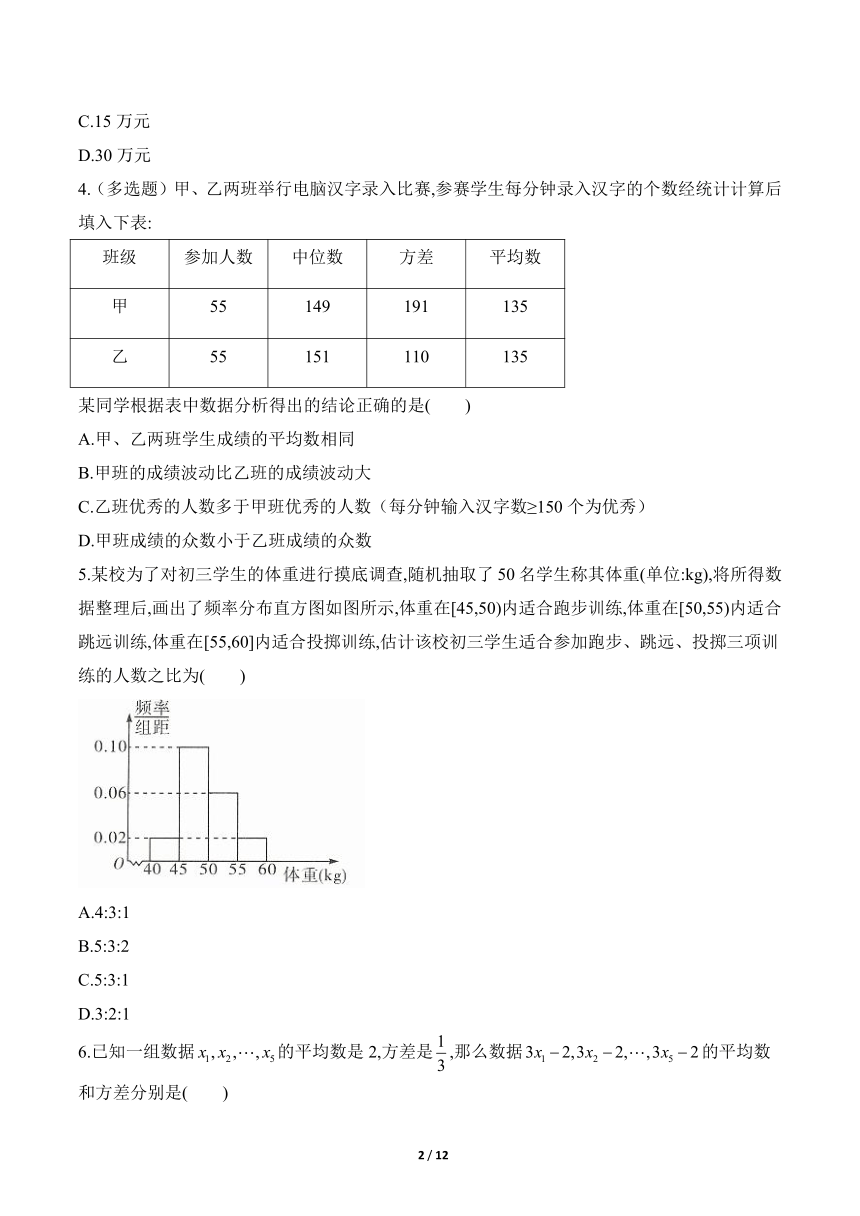
4.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据表中数据分析得出的结论正确的是( )
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
5.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生称其体重(单位:kg),将所得数据整理后,画出了频率分布直方图如图所示,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的人数之比为( )
A.4:3:1
B.5:3:2
C.5:3:1
D.3:2:1
6.已知一组数据的平均数是2,方差是,那么数据的平均数和方差分别是( )
A.2,3
B.2,1
C.
D.4,3
7.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,击命中目标得0分.两人4局的得分情况如下:
甲 6 6 9 9
乙 7 9
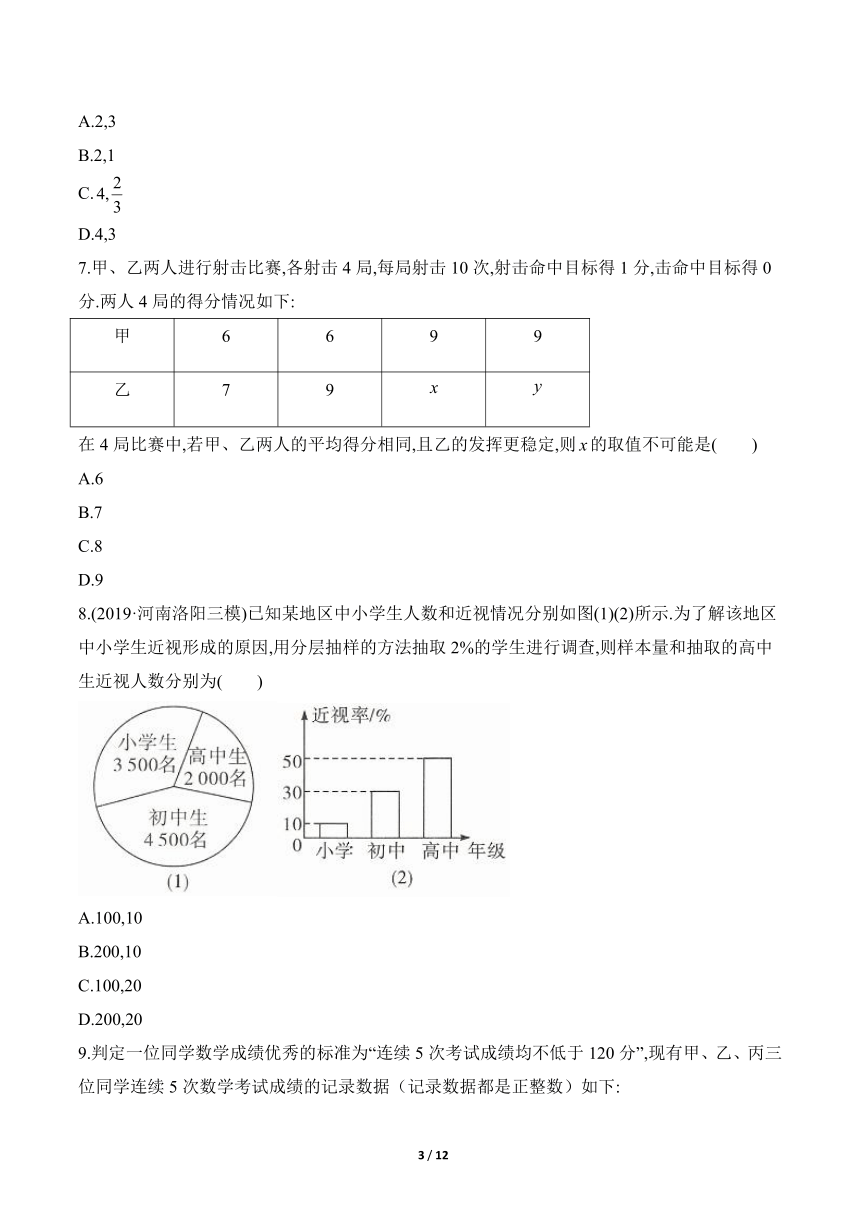
在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,则的取值不可能是( )
A.6
B.7
C.8
D.9
8.(2019·河南洛阳三模)已知某地区中小学生人数和近视情况分别如图(1)(2)所示.为了解该地区中小学生近视形成的原因,用分层抽样的方法抽取2%的学生进行调查,则样本量和抽取的高中生近视人数分别为( )
A.100,10
B.200,10
C.100,20
D.200,20
9.判定一位同学数学成绩优秀的标准为“连续5次考试成绩均不低于120分”,现有甲、乙、丙三位同学连续5次数学考试成绩的记录数据(记录数据都是正整数)如下:
①甲同学:5个数据的中位数为127,众数为120;
②乙同学:5个数据的中位数为125,平均数为127;
③丙同学:5个数据的中位数为135,平均数为128,方差为19.8.
则可以判定数学成绩优秀的同学为( )
A.甲、丙
B.乙、丙
C.甲、乙
D.甲、乙、丙
10.(多选题)在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数
B.平均数且标准差
C.平均数且极差小于或等于2
D.众数等于1且极差小于或等于4
二、填空题
11.1895年,在英国伦敦有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665~1666年的大瘟疫,人类学家分别测量了这些头盖骨的宽度(单位:mm),数据如下:
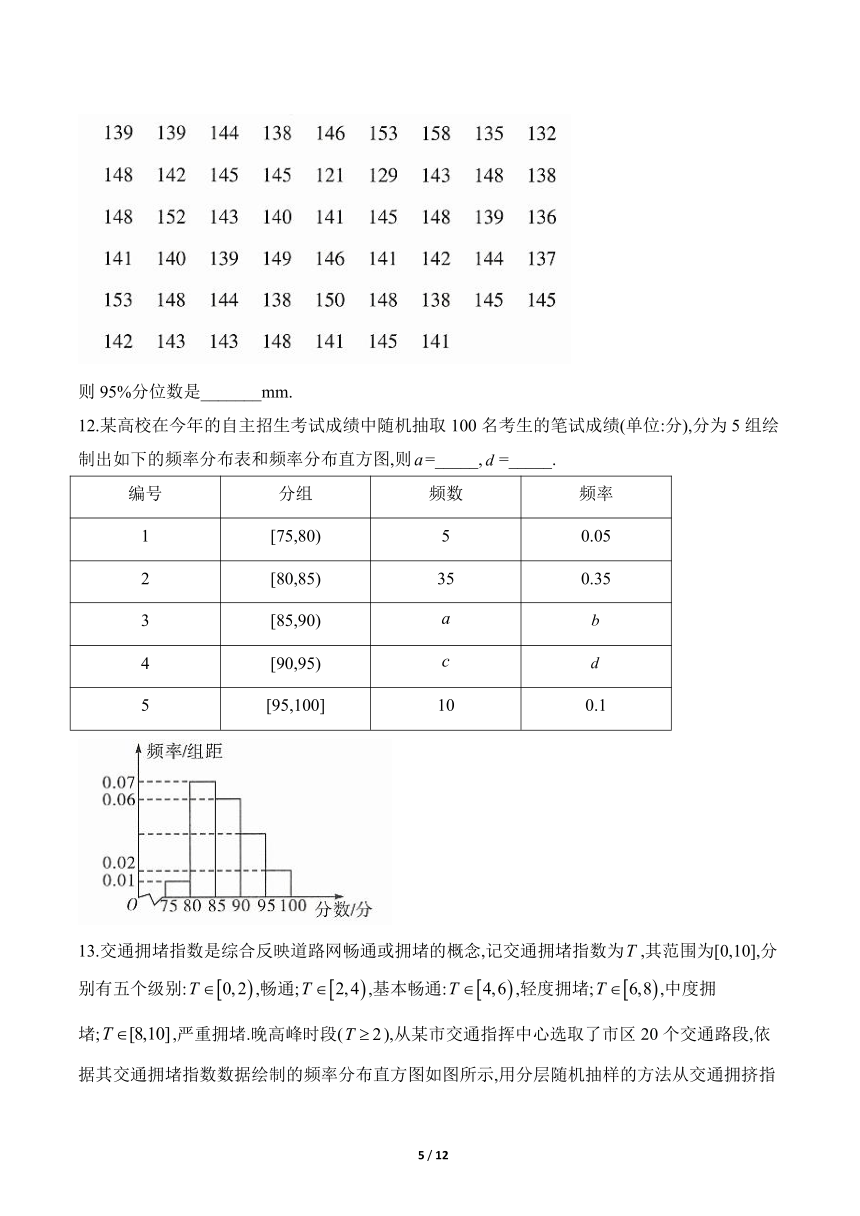
则95%分位数是_______mm.
12.某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩(单位:分),分为5组绘制出如下的频率分布表和频率分布直方图,则=_____,=_____.
编号 分组 频数 频率
1 [75,80) 5 0.05
2 [80,85) 35 0.35
3 [85,90)
4 [90,95)
5 [95,100] 10 0.1
13.交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为,其范围为[0,10],分别有五个级别:,畅通;,基本畅通:,轻度拥堵;,中度拥堵;,严重拥堵.晚高峰时段(),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的频率分布直方图如图所示,用分层随机抽样的方法从交通拥挤指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取_______个.
三、解答题
14.某市2019年4月1日~4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)列出频率分布表:
(2)作出频率分布直方图:
(3)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
15.某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对食堂服务质量的评分,绘制出了如图所示的频率分布直方图,其中样本数据分组为[40,50),[50,60),…,[90,100].
(1)求频率分布直方图中的值;
(2)若采用分层随机抽样的方式从评分在[40,60),[60,80),[80,100]的师生中抽取10人,则评分在[60,80)内的师生应抽取多少人
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿.用每组数据的中点值代替该组数据,试估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
16.在某校高一年级学生全部参加了体育科目的达标测试,从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,得到体育成绩的折线图.
(1)若体育成绩大于或等于70分的学生为“体育良生”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良生”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为,且,当三人的体育成绩方差最小时,写出的所有可能取值(不要求证明).
答案解析
一、选择题
1.答案:D
解析:本题考查了简单随机抽样的识别A不是简单随机抽样,因为是“一次性”抽取;B不是简单随机抽样,因为是“一次性”抽取;C不是简单随机抽样,因为是“一次性”抽取,且“总体容量无限”;D是简单随机抽样.
2.答案:D
解析:本题考查了利用随机数法抽样的方法和步骤,找到第2行第8列的数8开始往右读数,每次读取三位,超过800的数跳过去不读,前面已经读过的也跳过去不读,从而最先抽取的4件产品的编号依次是169,556,671,105.故抽取的第4件产品的编号是105.
3.答案:D
解析:本题考查了频率分布直方图的特征和频率的计算,由样本数据估计总体数据.由题可知,9时至14时的销售额的频率为0.1,因此9时至14时的销售总额为3÷0.1=30(万元).
4.答案:ABC
解析:本题考查了一组数据中的平均数、中位数、众数、方差的数字特征.甲、乙两班学生成绩的平均数都是135,故两班成绩的如乙班稳定,即甲班的成绩波动较大,B正确;甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,C正确;由题表看不出两班学生成绩的众数.
5.答案:
解析:本题考查了利用样本频率分布直方图估计总体的相关计算.体重在内的频率为,体重在,55)内的频率为,体重在内的频率为,因为,所以可估计该校初三学生适合参加跑步、跳远、投掷三项训练的人数之比为.
6.答案:D
解析:本题考查了-组数据中有关方差和平均数的线性计算公式.,,则又,.
7.答案:D
解析:本题考查了-组数据的离散程度.已知甲、乙两人的平均得分相同,,则.因为乙的发挥更稳定,可得,代入可得符合上述不等式,不可能是9.
8.答案:D
解析:本题考查了从统计图中读取数据并进行分析计算.本题需要将两个图表提供的信息结合起来,即可获得问题所需的信息.样本容量为,抽取的高中生人数为,由于其近视率为,所以近视的人数为.
9.答案:A
解析:本题考查了利用一组数据的平均数、中位数、众数、方差、标准差进行总体成绩评价,在①中,5个数据的中位数为127,众数为120,所以前三个数为120,120,127,则后两个数肯定大于127,故可以判定甲同学数学成绩优秀;在②中,举例如:118,119,125,133,140,这5个数据满足中位数为125,平均数为127,但不能判定乙同学数学成绩优秀;在③中,5个数据的中位数为135,平均数为128,方差为19.8,则标准差大于4小于5,所以丙成绩的最低分数在124与123之间,所以丙的成绩也为优秀.
10.答案:CD
解析:本题考查了一组数据中平均数、中位数、众数的计算.错,举反例:,其平均数,不符合指标.B错,举反例:,其平均数,且标准差,不符合指标.C对,若极差等于0或1,在的条件下,显然符合指标;若极差等于2且,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2),符合指标.D对,若众数等于1且极差小于或等于4,则最大值不超过5.
二、填空题
11.答案:149
解析:本题考查了一组数据中百分位数的计算公式.因为该样本共有106个数据,所以,将所有数据由小到大排列后,第101个数据是149,所以95%分位数是.
12.答案:30 0.2
解析:本题考查了频率分布表和直方图的特点,频率和频数的求解.由频率分布直方图可知,成绩在区间的频率,所以成绩在区间的人数.
13.答案:3
解析:本题考查了分层随机抽样的抽样比的相关计算.由频率分布直方图知,的路段共有(个),按分层随机抽样,从18个路段选出6个,抽样比为,因为)为中度拥堵的路段,应抽取(个).
三、解答题
14.答案:见解析
解析:(1)①求极差,;②确定组距与组数,以10为组距,分成7组:[41,51),[51,61),[61,71),[71,81),[81,91),[91,101),[101,111];③求出各组的频数,计算频率,列出频率分布表:
分组 频数 频率
[41,51) 2
[51,61) 1
[61,71) 4
[71,81) 6
[81,91) 10
[91,101) 5
[101,111] 2
(2)根据频率分布表,作出频率分布直方图如图所示.
(3)①该市一个月中空气污染指数有2天处于优的水平,占当月天数的;有26天处于良的水平,占当月天数的,优和良的天数为28天,占当月天数的说明该市空气质量基本良好.
②轻微污染有2天,占当月天数的;污染指数在80以上的接近轻微污染的天数为15,加上处于轻微污染的天数,共17天,占当月天数的,超过50%,说明该市空气质量有待进一步改善.
思路:本题考查了根据一组数据绘制频率分布表和频率分布直方图,根据数据的数字特征进行评价.
15.答案:见解析
解析:(1)由,解得.
(2)由频率分布直方图可知,评分在,内的师生人数之比为:,所以评分在内的师生应抽取5(人).
(3)由题中数据可得师生对食堂服务质量评分的平均分为.因为,所以食堂不需要内部整顿.
思路:本题考查了频率分布直方图的特征,频率的计算,抽样比的计算,用样本平均数估计总体平均数及评价.
16.答案:见解析
解析:(1)由折线图得体育成绩大于或等于70分的学生有(人),估计该校高一年级学生“体育良生”的人数为(人).
(2)估计该校高一年级学生达标测试的平均分77.25(分).
(3)因为甲、乙、丙三人的体育成绩分别为,且,其中,,所以当三人的体育成绩方差最小时,的所有可能取值为或.
思路:本题考查了统计图数据的读取,用样本数据估计总体数据,方差的求解.
3 / 12
一、选择题
1.下列抽样方法是简单随机抽样的是( )
A.从100个学生家长中一次性随机抽取10人做家访
B.从38本教辅参考资料中一次性随机抽取3本作为教学参考
C.从自然数集中一次性抽取20个进行奇偶性分析
D.某参会人员从最后一排20个座位中随机选择一个坐下
2.从800件产品中抽取60件进行质检,利用随机数法抽取样本时,先将800件产品按001,002,…,800进行编号,利用计算机随机产生如下0~9的随机数,现从第2行第8列的数8开始往右读数(三位三位地读),则抽取的第4件产品的编号是( )
A.169
B.556
C.671
D.105
3.某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,统计结果如下图所示.已知9时至10时的销售额为3万元,则9时至14时的销售总额为( )
A.10万元
B.12万元
C.15万元
D.30万元
4.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据表中数据分析得出的结论正确的是( )
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
5.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生称其体重(单位:kg),将所得数据整理后,画出了频率分布直方图如图所示,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的人数之比为( )
A.4:3:1
B.5:3:2
C.5:3:1
D.3:2:1
6.已知一组数据的平均数是2,方差是,那么数据的平均数和方差分别是( )
A.2,3
B.2,1
C.
D.4,3
7.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,击命中目标得0分.两人4局的得分情况如下:
甲 6 6 9 9
乙 7 9
在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,则的取值不可能是( )
A.6
B.7
C.8
D.9
8.(2019·河南洛阳三模)已知某地区中小学生人数和近视情况分别如图(1)(2)所示.为了解该地区中小学生近视形成的原因,用分层抽样的方法抽取2%的学生进行调查,则样本量和抽取的高中生近视人数分别为( )
A.100,10
B.200,10
C.100,20
D.200,20
9.判定一位同学数学成绩优秀的标准为“连续5次考试成绩均不低于120分”,现有甲、乙、丙三位同学连续5次数学考试成绩的记录数据(记录数据都是正整数)如下:
①甲同学:5个数据的中位数为127,众数为120;
②乙同学:5个数据的中位数为125,平均数为127;
③丙同学:5个数据的中位数为135,平均数为128,方差为19.8.
则可以判定数学成绩优秀的同学为( )
A.甲、丙
B.乙、丙
C.甲、乙
D.甲、乙、丙
10.(多选题)在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数
B.平均数且标准差
C.平均数且极差小于或等于2
D.众数等于1且极差小于或等于4
二、填空题
11.1895年,在英国伦敦有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665~1666年的大瘟疫,人类学家分别测量了这些头盖骨的宽度(单位:mm),数据如下:
则95%分位数是_______mm.
12.某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩(单位:分),分为5组绘制出如下的频率分布表和频率分布直方图,则=_____,=_____.
编号 分组 频数 频率
1 [75,80) 5 0.05
2 [80,85) 35 0.35
3 [85,90)
4 [90,95)
5 [95,100] 10 0.1
13.交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为,其范围为[0,10],分别有五个级别:,畅通;,基本畅通:,轻度拥堵;,中度拥堵;,严重拥堵.晚高峰时段(),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的频率分布直方图如图所示,用分层随机抽样的方法从交通拥挤指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取_______个.
三、解答题
14.某市2019年4月1日~4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)列出频率分布表:
(2)作出频率分布直方图:
(3)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
15.某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对食堂服务质量的评分,绘制出了如图所示的频率分布直方图,其中样本数据分组为[40,50),[50,60),…,[90,100].
(1)求频率分布直方图中的值;
(2)若采用分层随机抽样的方式从评分在[40,60),[60,80),[80,100]的师生中抽取10人,则评分在[60,80)内的师生应抽取多少人
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿.用每组数据的中点值代替该组数据,试估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
16.在某校高一年级学生全部参加了体育科目的达标测试,从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,得到体育成绩的折线图.
(1)若体育成绩大于或等于70分的学生为“体育良生”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良生”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为,且,当三人的体育成绩方差最小时,写出的所有可能取值(不要求证明).
答案解析
一、选择题
1.答案:D
解析:本题考查了简单随机抽样的识别A不是简单随机抽样,因为是“一次性”抽取;B不是简单随机抽样,因为是“一次性”抽取;C不是简单随机抽样,因为是“一次性”抽取,且“总体容量无限”;D是简单随机抽样.
2.答案:D
解析:本题考查了利用随机数法抽样的方法和步骤,找到第2行第8列的数8开始往右读数,每次读取三位,超过800的数跳过去不读,前面已经读过的也跳过去不读,从而最先抽取的4件产品的编号依次是169,556,671,105.故抽取的第4件产品的编号是105.
3.答案:D
解析:本题考查了频率分布直方图的特征和频率的计算,由样本数据估计总体数据.由题可知,9时至14时的销售额的频率为0.1,因此9时至14时的销售总额为3÷0.1=30(万元).
4.答案:ABC
解析:本题考查了一组数据中的平均数、中位数、众数、方差的数字特征.甲、乙两班学生成绩的平均数都是135,故两班成绩的如乙班稳定,即甲班的成绩波动较大,B正确;甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,C正确;由题表看不出两班学生成绩的众数.
5.答案:
解析:本题考查了利用样本频率分布直方图估计总体的相关计算.体重在内的频率为,体重在,55)内的频率为,体重在内的频率为,因为,所以可估计该校初三学生适合参加跑步、跳远、投掷三项训练的人数之比为.
6.答案:D
解析:本题考查了-组数据中有关方差和平均数的线性计算公式.,,则又,.
7.答案:D
解析:本题考查了-组数据的离散程度.已知甲、乙两人的平均得分相同,,则.因为乙的发挥更稳定,可得,代入可得符合上述不等式,不可能是9.
8.答案:D
解析:本题考查了从统计图中读取数据并进行分析计算.本题需要将两个图表提供的信息结合起来,即可获得问题所需的信息.样本容量为,抽取的高中生人数为,由于其近视率为,所以近视的人数为.
9.答案:A
解析:本题考查了利用一组数据的平均数、中位数、众数、方差、标准差进行总体成绩评价,在①中,5个数据的中位数为127,众数为120,所以前三个数为120,120,127,则后两个数肯定大于127,故可以判定甲同学数学成绩优秀;在②中,举例如:118,119,125,133,140,这5个数据满足中位数为125,平均数为127,但不能判定乙同学数学成绩优秀;在③中,5个数据的中位数为135,平均数为128,方差为19.8,则标准差大于4小于5,所以丙成绩的最低分数在124与123之间,所以丙的成绩也为优秀.
10.答案:CD
解析:本题考查了一组数据中平均数、中位数、众数的计算.错,举反例:,其平均数,不符合指标.B错,举反例:,其平均数,且标准差,不符合指标.C对,若极差等于0或1,在的条件下,显然符合指标;若极差等于2且,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2),符合指标.D对,若众数等于1且极差小于或等于4,则最大值不超过5.
二、填空题
11.答案:149
解析:本题考查了一组数据中百分位数的计算公式.因为该样本共有106个数据,所以,将所有数据由小到大排列后,第101个数据是149,所以95%分位数是.
12.答案:30 0.2
解析:本题考查了频率分布表和直方图的特点,频率和频数的求解.由频率分布直方图可知,成绩在区间的频率,所以成绩在区间的人数.
13.答案:3
解析:本题考查了分层随机抽样的抽样比的相关计算.由频率分布直方图知,的路段共有(个),按分层随机抽样,从18个路段选出6个,抽样比为,因为)为中度拥堵的路段,应抽取(个).
三、解答题
14.答案:见解析
解析:(1)①求极差,;②确定组距与组数,以10为组距,分成7组:[41,51),[51,61),[61,71),[71,81),[81,91),[91,101),[101,111];③求出各组的频数,计算频率,列出频率分布表:
分组 频数 频率
[41,51) 2
[51,61) 1
[61,71) 4
[71,81) 6
[81,91) 10
[91,101) 5
[101,111] 2
(2)根据频率分布表,作出频率分布直方图如图所示.
(3)①该市一个月中空气污染指数有2天处于优的水平,占当月天数的;有26天处于良的水平,占当月天数的,优和良的天数为28天,占当月天数的说明该市空气质量基本良好.
②轻微污染有2天,占当月天数的;污染指数在80以上的接近轻微污染的天数为15,加上处于轻微污染的天数,共17天,占当月天数的,超过50%,说明该市空气质量有待进一步改善.
思路:本题考查了根据一组数据绘制频率分布表和频率分布直方图,根据数据的数字特征进行评价.
15.答案:见解析
解析:(1)由,解得.
(2)由频率分布直方图可知,评分在,内的师生人数之比为:,所以评分在内的师生应抽取5(人).
(3)由题中数据可得师生对食堂服务质量评分的平均分为.因为,所以食堂不需要内部整顿.
思路:本题考查了频率分布直方图的特征,频率的计算,抽样比的计算,用样本平均数估计总体平均数及评价.
16.答案:见解析
解析:(1)由折线图得体育成绩大于或等于70分的学生有(人),估计该校高一年级学生“体育良生”的人数为(人).
(2)估计该校高一年级学生达标测试的平均分77.25(分).
(3)因为甲、乙、丙三人的体育成绩分别为,且,其中,,所以当三人的体育成绩方差最小时,的所有可能取值为或.
思路:本题考查了统计图数据的读取,用样本数据估计总体数据,方差的求解.
3 / 12
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
