人教A版(2019)高中数学必修第二册 《统计》单元测试(一)(word含解析)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《统计》单元测试(一)(word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 483.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览


文档简介
《统计》单元测试(一)
一、选择题
1.(2019·浙江嘉兴七校高一检测)下列两个抽样:①一个城市有210家某商品的代理商,其中大型代理商有20家,中型代理商有40家,小型代理商有150家,为了掌握该商品的销售情况,要从中抽取一个容量为21的样本;②某市质量检查人员从一食品生产企业生产的两箱(每箱12盒)牛奶中抽取4盒进行质量检查,则应采用的抽样方法依次为( )
A.简单随机抽样,简单随机抽样
B.分层随机抽样,分层随机抽样
C.分层随机抽样,简单随机抽样
D.简单随机抽样,分层随机抽样
2.某公司从代理的A,B,C,D四种产品中按分层随机抽样的方法抽取容量为110的样本,已知A,B,C,D四种产品的数量比是2:3:2:4,则该样本中D种产品的数量为( )
A.22件
B.33件
C.40件
D.55件
3.已知总体容量为106,若用随机数法抽取一个容量为10的样本,下面对总体的编号最方便的是( )
A.1,2,…,106
B.0,1,2,…,105
C.00,01,…,105
D.000,001,…,105
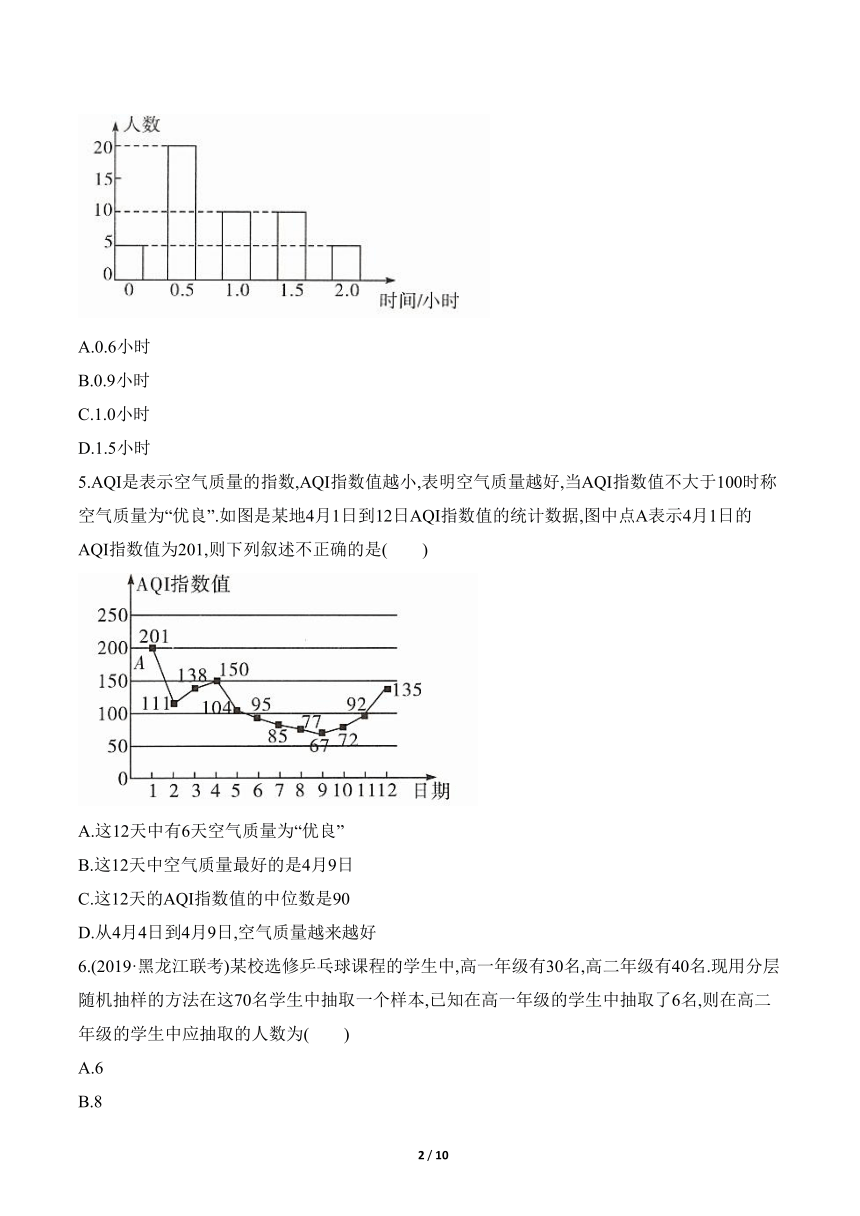
4.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的条形图(如图),根据条形图可得,这50名学生一天平均每人的课外阅读时间为( )
A.0.6小时
B.0.9小时
C.1.0小时
D.1.5小时
5.AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是4月9日
C.这12天的AQI指数值的中位数是90
D.从4月4日到4月9日,空气质量越来越好
6.(2019·黑龙江联考)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层随机抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6
B.8
C.10
D.12
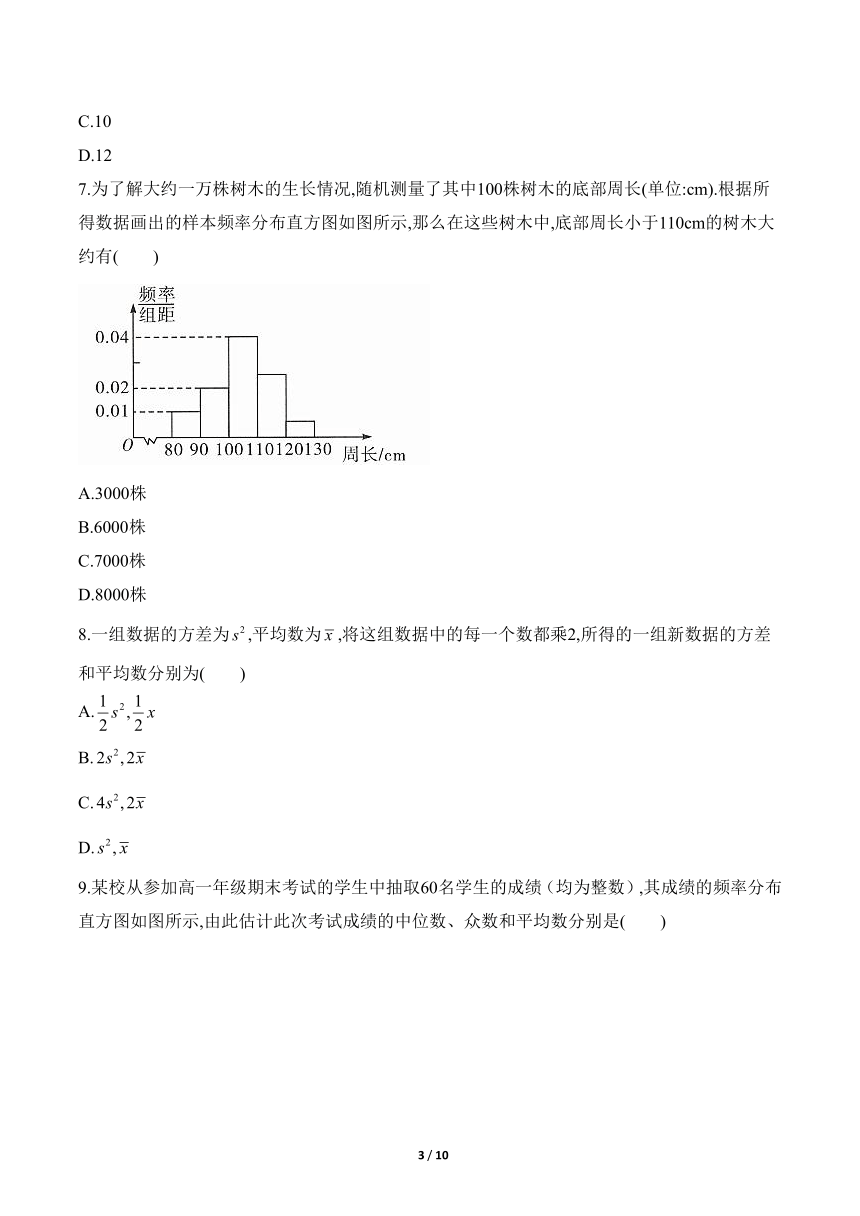
7.为了解大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这些树木中,底部周长小于110cm的树木大约有( )
A.3000株
B.6000株
C.7000株
D.8000株
8.一组数据的方差为,平均数为,将这组数据中的每一个数都乘2,所得的一组新数据的方差和平均数分别为( )
A.
B.
C.
D.
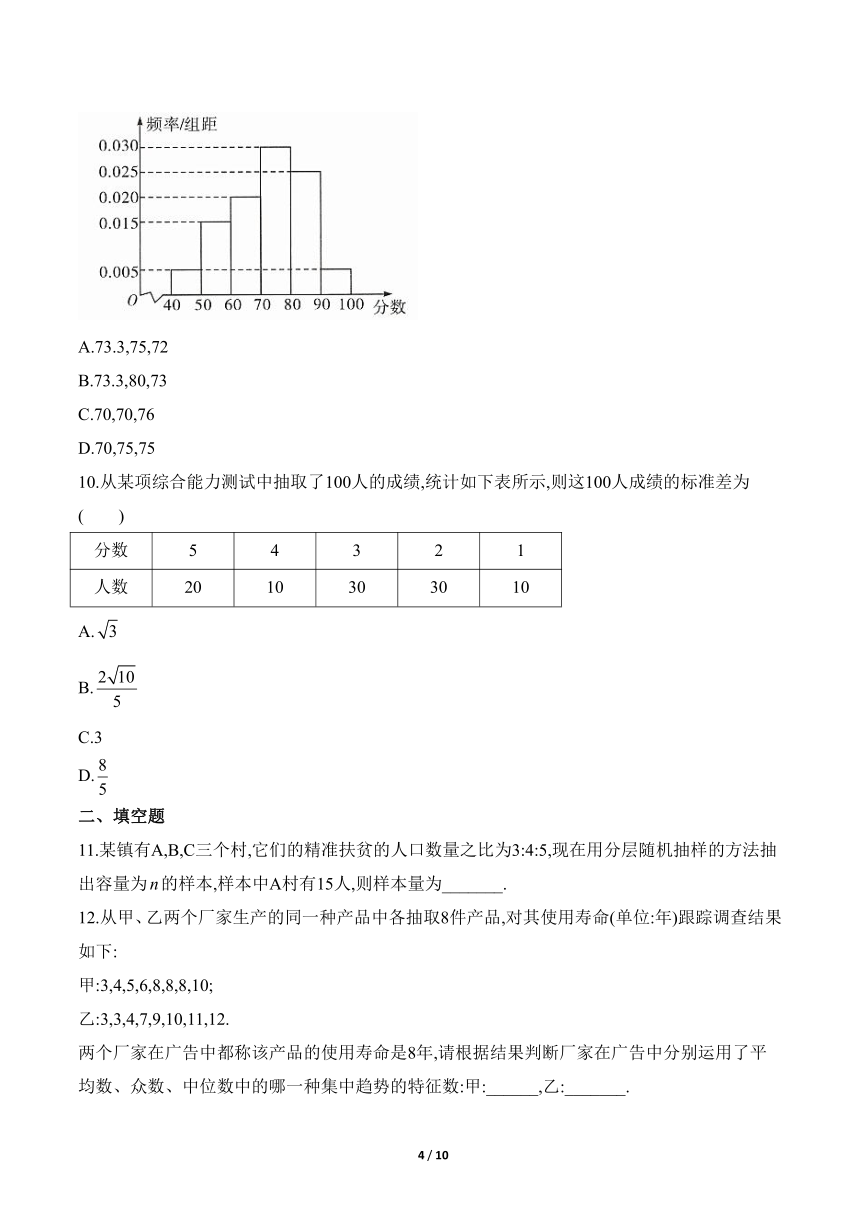
9.某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数、众数和平均数分别是( )
A.73.3,75,72
B.73.3,80,73
C.70,70,76
D.70,75,75
10.从某项综合能力测试中抽取了100人的成绩,统计如下表所示,则这100人成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A.
B.
C.3
D.
二、填空题
11.某镇有A,B,C三个村,它们的精准扶贫的人口数量之比为3:4:5,现在用分层随机抽样的方法抽出容量为的样本,样本中A村有15人,则样本量为_______.
12.从甲、乙两个厂家生产的同一种产品中各抽取8件产品,对其使用寿命(单位:年)跟踪调查结果如下:
甲:3,4,5,6,8,8,8,10;
乙:3,3,4,7,9,10,11,12.
两个厂家在广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲:______,乙:_______.
13.某市共有5000名高三学生参加联考,为了了解这些学生对数学知识的掌握情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成频率分布表:
分组 频数 频率
[80,90) ① ②
[90,100) 0.050
[100,110) 0.200
[110,120) 36 0.300
[120,130) 0.275
[130,140) 12
[140,150) 0.050
合计
根据上面的频率分布表,可知①处的数值为______,②处的数值为______.
三、解答题
14.化工厂三个车间共有工人1000名,各车间男、女工人数如下表:
车间 第一车间 第二车间 第三车间
女工人 173 100
男工人 177
已知在全厂工人中随机抽取1名,抽到第二车间男工人的可能性是0.15.
(1)求的值;
(2)现用分层随机抽样的方法在全厂抽取50名工人,则应在第三车间抽取多少名工人
15.100位居民的人均月用水量(单位:t)的分组及各组的频数如下:
(1)列出样本的频率分布表:
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为3t的标准,若超出标准,则超出部分加倍收费,当地政府说:“以上的居民用水不超过这个标准.”这个说法正确吗 为什么
16.春运期间,为了了解旅客购票情况,A随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(不完整):
分组 频数 频率
一组 0 0
二组 10 0.10
三组 10 ②
四组 ① 0.50
五组 30 0.30
合计 100 1.00
解答下列问题:
(1)这次抽样的样本量是多少
(2)在表中填写出①②处的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组
答案解析
一、选择题
1.答案:C
解析:本题考查了简单随机抽样和分层随机抽样的选取.①中商店的规模不同,所以应采用分层随机抽样;②中总体没有差异性,总量较小,样本量也较小,所以应采用简单随机抽样.
2.答案:C
解析:本题考查了分层随机抽样的容量计算问题.在分层随机抽样中,总体中产品数量比与抽取的样本中产品数量比相等,∴样本中种产品的数量为(件).
3.答案:D
解析:本题考查了简单随机抽样中随机数法的抽取原则.由随机数法抽取原则可知选D.
4.答案:B
解析:本题考查了条形图中的平均数问题.由条形图可得,这50名学生一天平均每人的课外阅读时间为(小时).
5.答案:C
解析:本题考查了从折线统计图中读取正确信息.由题图可知,AQI指数值不大于100的是6日到11日,共6天,所以中叙述正确;指数值最小的一天是4月9日为67,所以中叙述正确;中位数是99.5,所以中叙述错误;从题图中可以看出,4日到9日指数值越来越小,空气质量越来越好,所以中叙述正确.
6.答案:B
解析:本题考查了分层随机抽样中的抽样比,抽样比是按比例分配.高一年级有30名学生,且在高一年级的学生中抽取了6名,∴每个个体被抽到的抽样比是高二年级有40名学生,∴要抽取(名).
7.答案:C
解析:本题考查了利用样本频率分布直方图估计总体容量.
底部周长小于的频率为,故底部周长小于的树木大约有(株).
8.答案:C
解析:本题考查了求解一组线性相关数据的方差和平均数,熟记公式是解题的关键.设该组数据为,将这组数据中的每一个数都乘2,则有,平均数为.又,则新数据的方差为.
9.答案:
解析:本题考查了利用频率分布直方图求解平均数、中位数、众数.
频率分布直方图中最高矩形的底边中点的横坐标为数据的众数,故数据的众数为75,而中位数是把频率分布直方图分成左、右两个面积相等部分的平行于纵轴的直线与横轴交点的横坐标,由题图知,第一个小矩形的面积为,第二个小矩形的面积为,第三个小矩形的面积为,第四个小矩形的面积为,故将第四个小矩形的面积分成1:2的两部分即可,所以中位数是,组中值与频率之积的和为平均数,所以平均数为.
10.答案:B
解析:本题考查了标准差的求解公式.100人成绩的平均数是,标准差:
二、填空题
11.答案:60
解析:本题考查了利用分层随机抽样中比例分配求解样本量.样本量为.
12.答案:众数 中位数
解析:本题考查了利用样本的数字特征估计总体中数字特征的集中趋势.甲、乙两个厂家从不同角度描述了一组数据的特征.对甲分析:该组数据8出现的次数最多,故运用了众数;对乙分析:该组数据最中间的是7与9,故中位数是,故运用了中位数.
13.答案:3 0.025
解析:本题考查了频率分布表的特点和样本量的计算公式.
设样本量为,由位于的频数为36,频率为得样本量,所以的频率为.②处的数值为,①处的数值为.
三、解答题
14.答案:见解析
解析:(1)依题意,得,解得.(2)第一车间的工人数是,第二车间的I人数是,∴第三车间的工人数是.设应从第三车间抽取名工人,则有,解得,∴应在第三车间抽取20名工人.
思路:本题考查了分层随机抽样中的抽样比的相关计算.
15.答案:见解析
解析:(1)频率分布表:
分组 频率 频数
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1
(2)
众数:2.25,中位数:2.02,平均数:2.02.
(3)这个说法正确.理由:人均月用水量在3t及以上的居民所占的比例为6%+4%+2%=12%,即大约有12%的居民月用水量在3t及以上,88%的居民月用水量在3t以下,因此当地政府的说法是正确的.
思路:本题考查了频率分布表和频率分布直方图的绘制,利用频率分布直方图估计数据的平均数、中位数、众数,根据样本频率分布直方图对估计总体的情况及评价.
16.答案:见解析
解析:(1)样本量是100.
(2)①处填50,②处填0.10.
补全的频率分布直方图如图:
(3)设旅客平均购票用时为,则有.
即,所以旅客购票用时的平均数可能落在第四组.
思路:本题考查了频率分布表的特点、频率分布直方图的绘制、利用频率分布直方图求解平均数.
1 / 10
一、选择题
1.(2019·浙江嘉兴七校高一检测)下列两个抽样:①一个城市有210家某商品的代理商,其中大型代理商有20家,中型代理商有40家,小型代理商有150家,为了掌握该商品的销售情况,要从中抽取一个容量为21的样本;②某市质量检查人员从一食品生产企业生产的两箱(每箱12盒)牛奶中抽取4盒进行质量检查,则应采用的抽样方法依次为( )
A.简单随机抽样,简单随机抽样
B.分层随机抽样,分层随机抽样
C.分层随机抽样,简单随机抽样
D.简单随机抽样,分层随机抽样
2.某公司从代理的A,B,C,D四种产品中按分层随机抽样的方法抽取容量为110的样本,已知A,B,C,D四种产品的数量比是2:3:2:4,则该样本中D种产品的数量为( )
A.22件
B.33件
C.40件
D.55件
3.已知总体容量为106,若用随机数法抽取一个容量为10的样本,下面对总体的编号最方便的是( )
A.1,2,…,106
B.0,1,2,…,105
C.00,01,…,105
D.000,001,…,105
4.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的条形图(如图),根据条形图可得,这50名学生一天平均每人的课外阅读时间为( )
A.0.6小时
B.0.9小时
C.1.0小时
D.1.5小时
5.AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是4月9日
C.这12天的AQI指数值的中位数是90
D.从4月4日到4月9日,空气质量越来越好
6.(2019·黑龙江联考)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层随机抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6
B.8
C.10
D.12
7.为了解大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这些树木中,底部周长小于110cm的树木大约有( )
A.3000株
B.6000株
C.7000株
D.8000株
8.一组数据的方差为,平均数为,将这组数据中的每一个数都乘2,所得的一组新数据的方差和平均数分别为( )
A.
B.
C.
D.
9.某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数、众数和平均数分别是( )
A.73.3,75,72
B.73.3,80,73
C.70,70,76
D.70,75,75
10.从某项综合能力测试中抽取了100人的成绩,统计如下表所示,则这100人成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A.
B.
C.3
D.
二、填空题
11.某镇有A,B,C三个村,它们的精准扶贫的人口数量之比为3:4:5,现在用分层随机抽样的方法抽出容量为的样本,样本中A村有15人,则样本量为_______.
12.从甲、乙两个厂家生产的同一种产品中各抽取8件产品,对其使用寿命(单位:年)跟踪调查结果如下:
甲:3,4,5,6,8,8,8,10;
乙:3,3,4,7,9,10,11,12.
两个厂家在广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲:______,乙:_______.
13.某市共有5000名高三学生参加联考,为了了解这些学生对数学知识的掌握情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成频率分布表:
分组 频数 频率
[80,90) ① ②
[90,100) 0.050
[100,110) 0.200
[110,120) 36 0.300
[120,130) 0.275
[130,140) 12
[140,150) 0.050
合计
根据上面的频率分布表,可知①处的数值为______,②处的数值为______.
三、解答题
14.化工厂三个车间共有工人1000名,各车间男、女工人数如下表:
车间 第一车间 第二车间 第三车间
女工人 173 100
男工人 177
已知在全厂工人中随机抽取1名,抽到第二车间男工人的可能性是0.15.
(1)求的值;
(2)现用分层随机抽样的方法在全厂抽取50名工人,则应在第三车间抽取多少名工人
15.100位居民的人均月用水量(单位:t)的分组及各组的频数如下:
(1)列出样本的频率分布表:
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为3t的标准,若超出标准,则超出部分加倍收费,当地政府说:“以上的居民用水不超过这个标准.”这个说法正确吗 为什么
16.春运期间,为了了解旅客购票情况,A随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(不完整):
分组 频数 频率
一组 0 0
二组 10 0.10
三组 10 ②
四组 ① 0.50
五组 30 0.30
合计 100 1.00
解答下列问题:
(1)这次抽样的样本量是多少
(2)在表中填写出①②处的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组
答案解析
一、选择题
1.答案:C
解析:本题考查了简单随机抽样和分层随机抽样的选取.①中商店的规模不同,所以应采用分层随机抽样;②中总体没有差异性,总量较小,样本量也较小,所以应采用简单随机抽样.
2.答案:C
解析:本题考查了分层随机抽样的容量计算问题.在分层随机抽样中,总体中产品数量比与抽取的样本中产品数量比相等,∴样本中种产品的数量为(件).
3.答案:D
解析:本题考查了简单随机抽样中随机数法的抽取原则.由随机数法抽取原则可知选D.
4.答案:B
解析:本题考查了条形图中的平均数问题.由条形图可得,这50名学生一天平均每人的课外阅读时间为(小时).
5.答案:C
解析:本题考查了从折线统计图中读取正确信息.由题图可知,AQI指数值不大于100的是6日到11日,共6天,所以中叙述正确;指数值最小的一天是4月9日为67,所以中叙述正确;中位数是99.5,所以中叙述错误;从题图中可以看出,4日到9日指数值越来越小,空气质量越来越好,所以中叙述正确.
6.答案:B
解析:本题考查了分层随机抽样中的抽样比,抽样比是按比例分配.高一年级有30名学生,且在高一年级的学生中抽取了6名,∴每个个体被抽到的抽样比是高二年级有40名学生,∴要抽取(名).
7.答案:C
解析:本题考查了利用样本频率分布直方图估计总体容量.
底部周长小于的频率为,故底部周长小于的树木大约有(株).
8.答案:C
解析:本题考查了求解一组线性相关数据的方差和平均数,熟记公式是解题的关键.设该组数据为,将这组数据中的每一个数都乘2,则有,平均数为.又,则新数据的方差为.
9.答案:
解析:本题考查了利用频率分布直方图求解平均数、中位数、众数.
频率分布直方图中最高矩形的底边中点的横坐标为数据的众数,故数据的众数为75,而中位数是把频率分布直方图分成左、右两个面积相等部分的平行于纵轴的直线与横轴交点的横坐标,由题图知,第一个小矩形的面积为,第二个小矩形的面积为,第三个小矩形的面积为,第四个小矩形的面积为,故将第四个小矩形的面积分成1:2的两部分即可,所以中位数是,组中值与频率之积的和为平均数,所以平均数为.
10.答案:B
解析:本题考查了标准差的求解公式.100人成绩的平均数是,标准差:
二、填空题
11.答案:60
解析:本题考查了利用分层随机抽样中比例分配求解样本量.样本量为.
12.答案:众数 中位数
解析:本题考查了利用样本的数字特征估计总体中数字特征的集中趋势.甲、乙两个厂家从不同角度描述了一组数据的特征.对甲分析:该组数据8出现的次数最多,故运用了众数;对乙分析:该组数据最中间的是7与9,故中位数是,故运用了中位数.
13.答案:3 0.025
解析:本题考查了频率分布表的特点和样本量的计算公式.
设样本量为,由位于的频数为36,频率为得样本量,所以的频率为.②处的数值为,①处的数值为.
三、解答题
14.答案:见解析
解析:(1)依题意,得,解得.(2)第一车间的工人数是,第二车间的I人数是,∴第三车间的工人数是.设应从第三车间抽取名工人,则有,解得,∴应在第三车间抽取20名工人.
思路:本题考查了分层随机抽样中的抽样比的相关计算.
15.答案:见解析
解析:(1)频率分布表:
分组 频率 频数
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1
(2)
众数:2.25,中位数:2.02,平均数:2.02.
(3)这个说法正确.理由:人均月用水量在3t及以上的居民所占的比例为6%+4%+2%=12%,即大约有12%的居民月用水量在3t及以上,88%的居民月用水量在3t以下,因此当地政府的说法是正确的.
思路:本题考查了频率分布表和频率分布直方图的绘制,利用频率分布直方图估计数据的平均数、中位数、众数,根据样本频率分布直方图对估计总体的情况及评价.
16.答案:见解析
解析:(1)样本量是100.
(2)①处填50,②处填0.10.
补全的频率分布直方图如图:
(3)设旅客平均购票用时为,则有.
即,所以旅客购票用时的平均数可能落在第四组.
思路:本题考查了频率分布表的特点、频率分布直方图的绘制、利用频率分布直方图求解平均数.
1 / 10
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
