人教A版(2019)高中数学必修第二册 第九章_统计_复习与小结_章末练习(解析版)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 第九章_统计_复习与小结_章末练习(解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 284.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览




文档简介
一、选择题
1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A.抽签法 B.按性别分层随机抽样
C.按学段分层随机抽样 D.随机数法
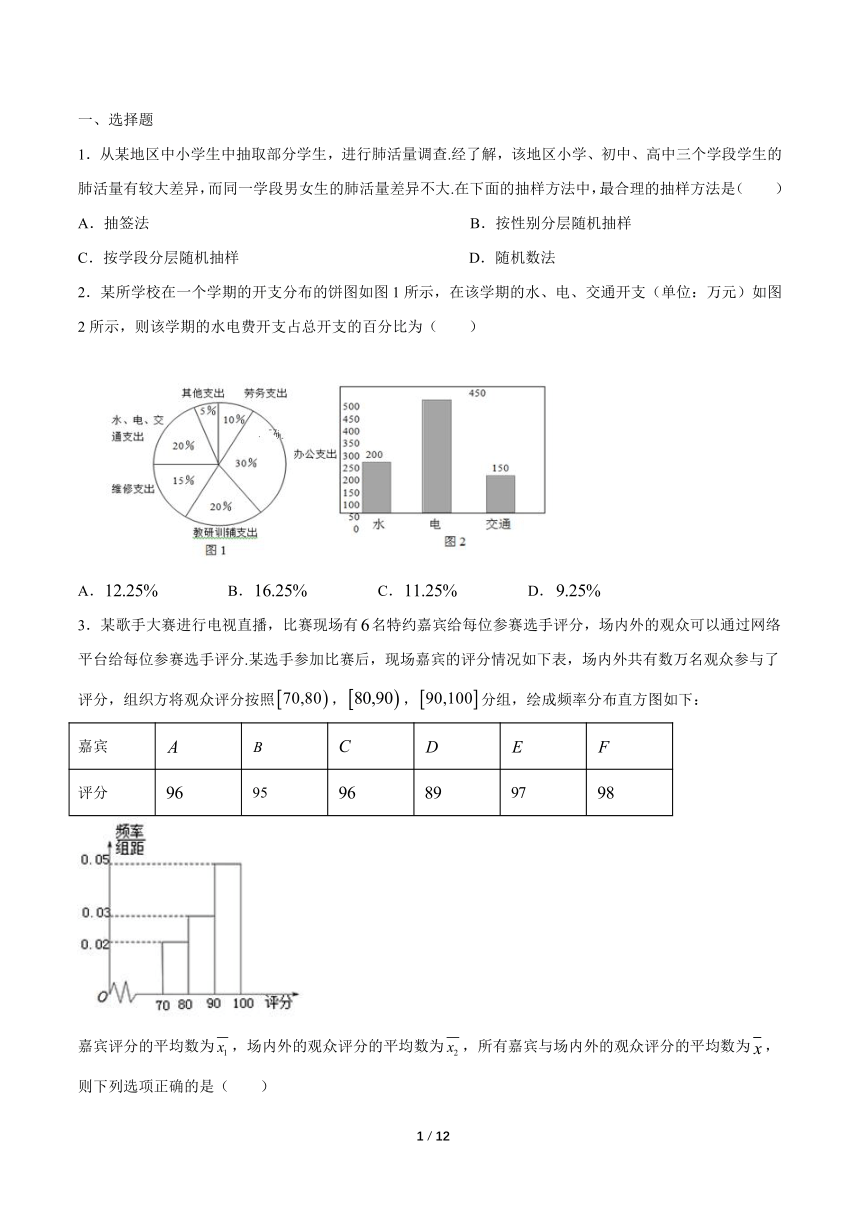
2.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的水电费开支占总开支的百分比为( )
A. B. C. D.
3.某歌手大赛进行电视直播,比赛现场有名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾的评分情况如下表,场内外共有数万名观众参与了评分,组织方将观众评分按照,,分组,绘成频率分布直方图如下:
嘉宾
评分
嘉宾评分的平均数为,场内外的观众评分的平均数为,所有嘉宾与场内外的观众评分的平均数为,则下列选项正确的是( )
A. B. C. D.
4.在第二次高考模拟市统测结束后,某校高三年级一个班级为预估本班学生的高考成绩水平,登记了全班同学的卷面成绩.经查询得知班上所有同学的学业水平考试成绩分加分均已取得,则学业水平考试加分分前后相比,不变的数字特征是( )
A.平均数 B.方差 C.中位数 D.众数
5.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表,某同学根据表中数据分析得出的结论正确的是( )
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
6.(多选题)在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数
B.平均数且标准差
C.平均数且极差小于或等于2
D.众数等于1且极差小于或等于4
二、填空题
7.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
8.1895年,在英国伦敦有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665~1666年的大瘟疫人类学家分别测量了这些头盖骨的宽度(单位:mm),数据如下:
146 141 139 140 145 141 142 131 142
140 144 140 138 139 147 139 141 137
141 132 140 140 141 143 134 146 134
142 133 149 140 140 143 143 149 136
141 143 143 141 138 136 138 144 136
145 143 137 142 146 140 148 140 140
139 139 144 138 146 153 158 135 132
148 142 145 145 121 129 143 148 138
148 152 143 140 141 145 148 139 136
141 140 139 149 146 141 142 144 137
153 148 144 138 150 148 138 145 145
142 143 143 148 141 145 141
则95%分位数是________mm.
9.交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取_____个.
10.一个项目由15个专家评委投票表决,剔除一个最高分96,一个最低分58后所得到的平均分为92,方差为16,那么原始得分的方差为______________.
三、解答题
11.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
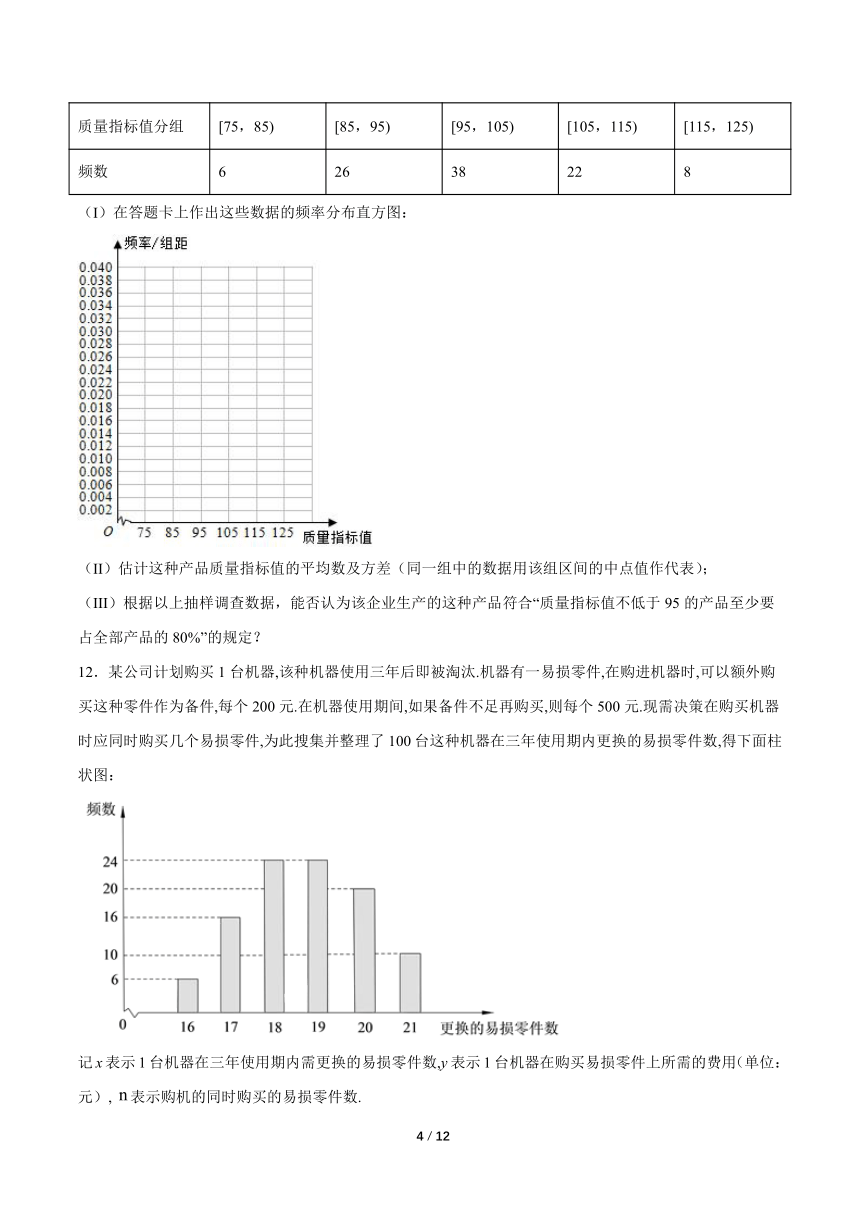
12.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),表示购机的同时购买的易损零件数.
(Ⅰ)若=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
答案
一、选择题
1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A.抽签法 B.按性别分层随机抽样
C.按学段分层随机抽样 D.随机数法
【答案】C
【解析】小学、初中、高中三个学段学生的肺活量有较大差异 学段对统计结果影响较大
同一学段男女生肺活量差异不大 性别对统计结果无明显影响最合理的抽样方法是按学段分层随机抽样.故选:
2.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的水电费开支占总开支的百分比为( )
A. B. C. D.
【答案】B
【解析】由图知,水、电支出占水、电、交通支出的比例为,
由图知,水、电、交通支出占学校一个学期总开支的比例为,因此,该学期的水电费开支占总开支的百分比为,故选:B。
3.某歌手大赛进行电视直播,比赛现场有名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾的评分情况如下表,场内外共有数万名观众参与了评分,组织方将观众评分按照,,分组,绘成频率分布直方图如下:
嘉宾
评分
嘉宾评分的平均数为,场内外的观众评分的平均数为,所有嘉宾与场内外的观众评分的平均数为,则下列选项正确的是( )
A. B. C. D.
【答案】C
【解析】由表格中的数据可知,,
由频率分布直方图可知,,则,
由于场外有数万名观众,所以,.故选:B.
4.在第二次高考模拟市统测结束后,某校高三年级一个班级为预估本班学生的高考成绩水平,登记了全班同学的卷面成绩.经查询得知班上所有同学的学业水平考试成绩分加分均已取得,则学业水平考试加分分前后相比,不变的数字特征是( )
A.平均数 B.方差 C.中位数 D.众数
【答案】B
【解析】学业水平考试加分分前后相比,平均数、中位数、众数都在原来的基础上加上了,而全班的成绩波动性没发生变化,即方差没变.故选:B.
5.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表,某同学根据表中数据分析得出的结论正确的是( )
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
【答案】ABC
【解析】甲、乙两班学生成绩的平均数都是35,故两班成绩的平均数相同,A正确;,甲班成绩不如乙班稳定,即甲班的成绩波动较大,B正确.
甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,C正确;由题表看不出两班学生成绩的众数,D错误.故选:ABC
6.(多选题)在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数
B.平均数且标准差
C.平均数且极差小于或等于2
D.众数等于1且极差小于或等于4
【答案】CD
【解析】A错,举反例:0,0,0,0,2,6,6,其平均数,不符合指标.
B错,举反例:0,3,3,3,3,3,6,其平均数,且标准差,不符合指标C对,若极差等于0或1,在的条件下,显然符合指标;若极差等于2且,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标D对,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.故选:.
二、填空题
7.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
【答案】0.98.
【解析】由题意得,经停该高铁站的列车正点数约为,其中高铁个数为10+20+10=40,所以该站所有高铁平均正点率约为.
8.1895年,在英国伦敦有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665~1666年的大瘟疫人类学家分别测量了这些头盖骨的宽度(单位:mm),数据如下:
146 141 139 140 145 141 142 131 142
140 144 140 138 139 147 139 141 137
141 132 140 140 141 143 134 146 134
142 133 149 140 140 143 143 149 136
141 143 143 141 138 136 138 144 136
145 143 137 142 146 140 148 140 140
139 139 144 138 146 153 158 135 132
148 142 145 145 121 129 143 148 138
148 152 143 140 141 145 148 139 136
141 140 139 149 146 141 142 144 137
153 148 144 138 150 148 138 145 145
142 143 143 148 141 145 141
则95%分位数是________mm.
【答案】149
【解析】因为该样本共有106个数据,所以,
将所有数据由小到大排列后,第101个数据是149,所以95%分位数是149mm.故答案为:
9.交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取_____个.
【答案】3
【解析】由频率分布直方图知,,的路段共有(个),按分层抽样,从个路段选出个,抽样比为.
∵中度拥堵∴中度拥堵的路段应抽取(个).
10.一个项目由15个专家评委投票表决,剔除一个最高分96,一个最低分58后所得到的平均分为92,方差为16,那么原始得分的方差为______________.
【答案】
【解析】剔除最高分和最低分后的
则原始平均分
原始
原始方差 即原始方差为 88 .
三、解答题
11.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
【答案】(1)见解析;(2)平均数100,方差为104;(3)不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
【解析】(1)直方图如图,
(2)质量指标值的样本平均数为
.
质量指标值的样本方差为
.
(3)质量指标值不低于95的产品所占比例的估计值为
,
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
12.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),表示购机的同时购买的易损零件数.
(Ⅰ)若=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
【答案】(1);(2)19;
(3) 购买1台机器的同时应购买19个易损零件.
【解析】(Ⅰ)当时,;当时,,
所以与的函数解析式为.
(Ⅱ)由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故的最小值为19.
(Ⅲ)若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3 800,20台的费用为4 300,10台的费用为4 800,因此这100台机器在购买易损零件上所需费用的平均数为.
若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4 000,10台的费用为4 500,因此这100台机器在购买易损零件上所需费用的平均数为.
比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
5 / 12
1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A.抽签法 B.按性别分层随机抽样
C.按学段分层随机抽样 D.随机数法
2.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的水电费开支占总开支的百分比为( )
A. B. C. D.
3.某歌手大赛进行电视直播,比赛现场有名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾的评分情况如下表,场内外共有数万名观众参与了评分,组织方将观众评分按照,,分组,绘成频率分布直方图如下:
嘉宾
评分
嘉宾评分的平均数为,场内外的观众评分的平均数为,所有嘉宾与场内外的观众评分的平均数为,则下列选项正确的是( )
A. B. C. D.
4.在第二次高考模拟市统测结束后,某校高三年级一个班级为预估本班学生的高考成绩水平,登记了全班同学的卷面成绩.经查询得知班上所有同学的学业水平考试成绩分加分均已取得,则学业水平考试加分分前后相比,不变的数字特征是( )
A.平均数 B.方差 C.中位数 D.众数
5.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表,某同学根据表中数据分析得出的结论正确的是( )
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
6.(多选题)在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数
B.平均数且标准差
C.平均数且极差小于或等于2
D.众数等于1且极差小于或等于4
二、填空题
7.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
8.1895年,在英国伦敦有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665~1666年的大瘟疫人类学家分别测量了这些头盖骨的宽度(单位:mm),数据如下:
146 141 139 140 145 141 142 131 142
140 144 140 138 139 147 139 141 137
141 132 140 140 141 143 134 146 134
142 133 149 140 140 143 143 149 136
141 143 143 141 138 136 138 144 136
145 143 137 142 146 140 148 140 140
139 139 144 138 146 153 158 135 132
148 142 145 145 121 129 143 148 138
148 152 143 140 141 145 148 139 136
141 140 139 149 146 141 142 144 137
153 148 144 138 150 148 138 145 145
142 143 143 148 141 145 141
则95%分位数是________mm.
9.交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取_____个.
10.一个项目由15个专家评委投票表决,剔除一个最高分96,一个最低分58后所得到的平均分为92,方差为16,那么原始得分的方差为______________.
三、解答题
11.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
12.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),表示购机的同时购买的易损零件数.
(Ⅰ)若=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
答案
一、选择题
1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A.抽签法 B.按性别分层随机抽样
C.按学段分层随机抽样 D.随机数法
【答案】C
【解析】小学、初中、高中三个学段学生的肺活量有较大差异 学段对统计结果影响较大
同一学段男女生肺活量差异不大 性别对统计结果无明显影响最合理的抽样方法是按学段分层随机抽样.故选:
2.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的水电费开支占总开支的百分比为( )
A. B. C. D.
【答案】B
【解析】由图知,水、电支出占水、电、交通支出的比例为,
由图知,水、电、交通支出占学校一个学期总开支的比例为,因此,该学期的水电费开支占总开支的百分比为,故选:B。
3.某歌手大赛进行电视直播,比赛现场有名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾的评分情况如下表,场内外共有数万名观众参与了评分,组织方将观众评分按照,,分组,绘成频率分布直方图如下:
嘉宾
评分
嘉宾评分的平均数为,场内外的观众评分的平均数为,所有嘉宾与场内外的观众评分的平均数为,则下列选项正确的是( )
A. B. C. D.
【答案】C
【解析】由表格中的数据可知,,
由频率分布直方图可知,,则,
由于场外有数万名观众,所以,.故选:B.
4.在第二次高考模拟市统测结束后,某校高三年级一个班级为预估本班学生的高考成绩水平,登记了全班同学的卷面成绩.经查询得知班上所有同学的学业水平考试成绩分加分均已取得,则学业水平考试加分分前后相比,不变的数字特征是( )
A.平均数 B.方差 C.中位数 D.众数
【答案】B
【解析】学业水平考试加分分前后相比,平均数、中位数、众数都在原来的基础上加上了,而全班的成绩波动性没发生变化,即方差没变.故选:B.
5.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表,某同学根据表中数据分析得出的结论正确的是( )
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
【答案】ABC
【解析】甲、乙两班学生成绩的平均数都是35,故两班成绩的平均数相同,A正确;,甲班成绩不如乙班稳定,即甲班的成绩波动较大,B正确.
甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,C正确;由题表看不出两班学生成绩的众数,D错误.故选:ABC
6.(多选题)在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数
B.平均数且标准差
C.平均数且极差小于或等于2
D.众数等于1且极差小于或等于4
【答案】CD
【解析】A错,举反例:0,0,0,0,2,6,6,其平均数,不符合指标.
B错,举反例:0,3,3,3,3,3,6,其平均数,且标准差,不符合指标C对,若极差等于0或1,在的条件下,显然符合指标;若极差等于2且,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标D对,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.故选:.
二、填空题
7.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
【答案】0.98.
【解析】由题意得,经停该高铁站的列车正点数约为,其中高铁个数为10+20+10=40,所以该站所有高铁平均正点率约为.
8.1895年,在英国伦敦有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665~1666年的大瘟疫人类学家分别测量了这些头盖骨的宽度(单位:mm),数据如下:
146 141 139 140 145 141 142 131 142
140 144 140 138 139 147 139 141 137
141 132 140 140 141 143 134 146 134
142 133 149 140 140 143 143 149 136
141 143 143 141 138 136 138 144 136
145 143 137 142 146 140 148 140 140
139 139 144 138 146 153 158 135 132
148 142 145 145 121 129 143 148 138
148 152 143 140 141 145 148 139 136
141 140 139 149 146 141 142 144 137
153 148 144 138 150 148 138 145 145
142 143 143 148 141 145 141
则95%分位数是________mm.
【答案】149
【解析】因为该样本共有106个数据,所以,
将所有数据由小到大排列后,第101个数据是149,所以95%分位数是149mm.故答案为:
9.交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取_____个.
【答案】3
【解析】由频率分布直方图知,,的路段共有(个),按分层抽样,从个路段选出个,抽样比为.
∵中度拥堵∴中度拥堵的路段应抽取(个).
10.一个项目由15个专家评委投票表决,剔除一个最高分96,一个最低分58后所得到的平均分为92,方差为16,那么原始得分的方差为______________.
【答案】
【解析】剔除最高分和最低分后的
则原始平均分
原始
原始方差 即原始方差为 88 .
三、解答题
11.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
【答案】(1)见解析;(2)平均数100,方差为104;(3)不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
【解析】(1)直方图如图,
(2)质量指标值的样本平均数为
.
质量指标值的样本方差为
.
(3)质量指标值不低于95的产品所占比例的估计值为
,
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
12.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),表示购机的同时购买的易损零件数.
(Ⅰ)若=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
【答案】(1);(2)19;
(3) 购买1台机器的同时应购买19个易损零件.
【解析】(Ⅰ)当时,;当时,,
所以与的函数解析式为.
(Ⅱ)由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故的最小值为19.
(Ⅲ)若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3 800,20台的费用为4 300,10台的费用为4 800,因此这100台机器在购买易损零件上所需费用的平均数为.
若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4 000,10台的费用为4 500,因此这100台机器在购买易损零件上所需费用的平均数为.
比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
5 / 12
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
