人教A版(2019)高中数学必修第二册 第九章_统计测试(word含解析)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 第九章_统计测试(word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 428.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 16:08:17 | ||
图片预览




文档简介
第九章 统计数测试
一.选择题(每题5分,共60分)
1.①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;③运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这三件事,恰当的抽样方法分别为( )
A.分层抽样,分层抽样,简单随机抽样
B.系统抽样,系统抽样,简单随机抽样
C.分层抽样,简单随机抽样,简单随机抽样
D.系统抽样,分层抽样,简单随机抽样
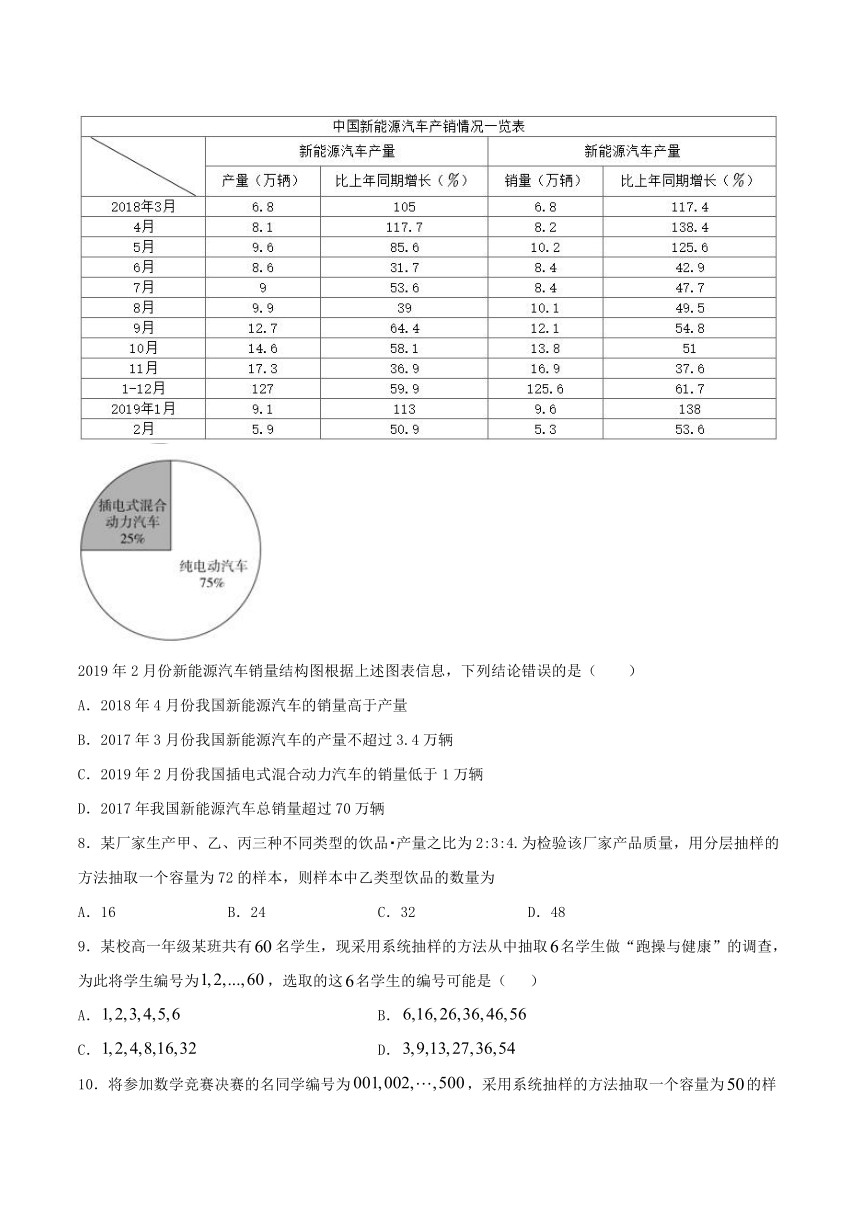
2.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A.90 B.75 C.60 D.45
3.某中学有高中生人,初中生人,男、女生所占的比例如下图所示.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从高中生中抽取女生人,则从初中生中抽取的男生人数是( )
A. B. C. D.
4.某影院有60排座位,每排70个座号,一次报告会坐满了听众,会后留下座号为15的所有听众60人进行座谈,这是运用了( )
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
5.甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,分别表示甲、乙两名运动员这项测试成绩的平均数,分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
A.
B.
C.
D.
6.(2016 浦东新区一模)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x﹣y|的值为( )
A.1 B.2 C.3 D.4
7.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是( )
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
8.某厂家生产甲、乙、丙三种不同类型的饮品 产量之比为2:3:4.为检验该厂家产品质量,用分层抽样的方法抽取一个容量为72的样本,则样本中乙类型饮品的数量为
A.16 B.24 C.32 D.48
9.某校高一年级某班共有名学生,现采用系统抽样的方法从中抽取名学生做“跑操与健康”的调查,为此将学生编号为,选取的这名学生的编号可能是( )
A. B.
C. D.
10.将参加数学竞赛决赛的名同学编号为,采用系统抽样的方法抽取一个容量为的样本,且随机抽到的号码为,这名同学分别在三个考试点考试,从到在第一考点,从到在第二考点,从到在第三考点,则第二考点被抽中的人数为( )
A. B. C. D.
11.一个蜂巢里有1只蜜蜂,第一天,它飞出去带回了5个伙伴;第二天,6只蜜蜂飞出去各自带回了5个伙伴........如果这个过程继续下去,那么第6天所有的蜜蜂归巢后,蜂巢中共有蜜蜂多少只( )
A. B. C. D.
12.甲、乙两名选手参加歌手大赛时,5名评委打的分数用如图所示的茎叶图表示,s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ).
A.s1>s2 B.s1=s2 C.s1<s2 D.不确定
填空题(每题5分,共20分)
13.某校女子篮球队7名运动员身高(单位:cm)分布的茎叶图如图,已知记录的平均身高为175 cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数字记为x,那么x的值为________.
14.某校高三年级500名学生中,血型为O型的有200人,A型的有125人,B型的有125人,AB型的有50人.为研究血型与色弱之间的关系,现用分层抽样的方法从这500名学生中抽取一个容量为60的样本,则应抽取____名血型为AB的学生.
15.空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良()的天数(按这个月总共30天计算)为________.
16.校开展“爱我南阳、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是__________.
三.解答题(17题10分,其余12分/题,共70分)
17.某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.
18.一微商店对某种产品每天的销售量(件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
(1)求频率分布直方图中的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
19.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下:求:
(1)根据直方图可得这100名学生中体重在(56,64)的学生人数.
(2)请根据上面的频率分布直方图估计该地区17.5-18岁的男生体重.
(3)若在这100名男生中随意抽取1人,该生体重低于62的概率是多少?
20.如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
21.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这 50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布图中的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在的受访职工中,随机抽取2人,求此2人评分都在 的概率.
22.某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
第九章统计测试答案
一.选择题(每题5分,共60分)
1.①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;③运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这三件事,恰当的抽样方法分别为( )
A.分层抽样,分层抽样,简单随机抽样
B.系统抽样,系统抽样,简单随机抽样
C.分层抽样,简单随机抽样,简单随机抽样
D.系统抽样,分层抽样,简单随机抽样
【来源】沈阳市2016-2017学年度(下)部分市级重点高中协作校期中测试高一数学试题
【答案】D
【解析】
①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查,此项调查的总体数目较多,而且差异不大,符合系统抽样的适用范围.
②一次数学月考中,某班有10人在100分以上,32人在90 100分,12人低于90分,现从中抽取9人了解有关情况,此项抽查的总体数目较多,而且差异很大,符合分层抽样的适用范围.
③运动会工作人员为参加4×100m接力赛的6支队伍安排跑道,此项抽查,的总体个数不多,而且差异不大,符合简单随机抽样的适用范围.
本题选择D选项.
2.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A.90 B.75 C.60 D.45
【答案】A
【解析】样本中产品净重小于100克的频率为(0.050+0.100)×2=0.3,频数为36,
∴样本总数为.
∵样本中净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.75,
∴样本中净重大于或等于98克并且小于104克的产品的个数为120×0.75=90.
3.某中学有高中生人,初中生人,男、女生所占的比例如下图所示.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从高中生中抽取女生人,则从初中生中抽取的男生人数是( )
A. B. C. D.
【来源】河南省信阳高级中学2019届高三第一次大考数学(文)试题
【答案】A
【解析】
分析:首先确定分层抽样的抽取比例,然后求解初中生中抽取的男生人数即可.
详解:因为分层抽样的抽取比例为,
所以初中生中抽取的男生人数是人.
本题选择A选项.
4.某影院有60排座位,每排70个座号,一次报告会坐满了听众,会后留下座号为15的所有听众60人进行座谈,这是运用了( )
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
【来源】陕西省黄陵中学2016-2017学年高一(普通班)下学期期末考试数学试题
【答案】C
【解析】∵听众人数比较多,
∵把每排听众从1到70号编排,
要求每班编号为15的同学留下进行交流,
这样选出的样本是采用系统抽样的方法,
故选C.
5.甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,分别表示甲、乙两名运动员这项测试成绩的平均数,分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
A.
B.
C.
D.
【来源】2018年春人教A版高中数学必修三单元测试:第二章 统计
【答案】D
【解析】
由甲、乙两名运动员在某项测试中的6次成绩的茎叶图可得,
=15,=15,
×[(-6)2+(-1)2+02+02+12+62]=×[(-7)2+(-2)2+02+02+22+72]=.
所以 .选D.
6.(2016 浦东新区一模)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x﹣y|的值为( )
A.1 B.2 C.3 D.4
【来源】2015-2016学年云南省景洪市三中高二上学期期中考试数学试卷(带解析)
【答案】D
【解析】由题意这组数据的平均数为10,方差为2可得:x+y=20,(x﹣10)2+(y﹣10)2=8,
解这个方程组需要用一些技巧,
因为不要直接求出x、y,只要求出|x﹣y|,
设x=10+t,y=10﹣t,由(x﹣10)2+(y﹣10)2=8得t2=4;
∴|x﹣y|=2|t|=4,
故选D.
7.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是( )
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
【来源】山东省济南市2019届高三5月学习质量针对性检测理科数学试题
【答案】C
【解析】由图表可知:
对于选项A中,2018年4月份我国新能源汽车的销量为8.2万辆,产量为8.1万辆,所以是正确的;
对于选项B中,2017年3月份我国新能源汽车的产量为万辆,所以是正确的;
对于选项C中,2019年2月份我国插电混合动力汽车的销量为万辆,所以不正确;
对于D中,2017年我国新能源汽车总销量为万辆,所以是正确的,
故选C.
8.某厂家生产甲、乙、丙三种不同类型的饮品 产量之比为2:3:4.为检验该厂家产品质量,用分层抽样的方法抽取一个容量为72的样本,则样本中乙类型饮品的数量为( )
A.16 B.24 C.32 D.48
【来源】河南省洛阳市2018-2019学年高一下学期期末数学试题
【答案】B
【解析】因为分层抽样总体和各层的抽样比例相同,
所以各层在总体的比例与在样本的比例相同,
所以样本中乙类型饮品的数量为.
故选B.
9.某校高一年级某班共有名学生,现采用系统抽样的方法从中抽取名学生做“跑操与健康”的调查,为此将学生编号为,选取的这名学生的编号可能是( )
A. B.
C. D.
【来源】2013届河北省石家庄市高中毕业班第一次模拟考试文科数学试卷A(带解析)
【答案】B
【解析】根据系统抽样的定义,从60名学生中抽取6名学生,编号的间隔为
∴编号组成的数列应是公差为10的等差数列,故选B.
10.将参加数学竞赛决赛的名同学编号为,采用系统抽样的方法抽取一个容量为的样本,且随机抽到的号码为,这名同学分别在三个考试点考试,从到在第一考点,从到在第二考点,从到在第三考点,则第二考点被抽中的人数为( )
A. B. C. D.
【来源】江西省新八校2019届高三第二次联考文科数学试题
【答案】C
【解析】系统抽样的分段间隔为,在随机抽样中,首次抽到号,以后每隔个号抽到一个人,则,在至号中共有17人被抽中,其编号分别为.
故选C
11.一个蜂巢里有1只蜜蜂,第一天,它飞出去带回了5个伙伴;第二天,6只蜜蜂飞出去各自带回了5个伙伴........如果这个过程继续下去,那么第6天所有的蜜蜂归巢后,蜂巢中共有蜜蜂多少只( )
A. B. C. D.
【来源】陕西省渭南市尚德中学2017-2018学年高二第一次教学质量检测数学试卷
【答案】B
【解析】第一天归巢后共有6个,第二天归巢后,共有,第三天归巢后,共有,以此类推,第六天归巢后,共有,故选B.
12.甲、乙两名选手参加歌手大赛时,5名评委打的分数用如图所示的茎叶图表示,s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ).
A.s1>s2 B.s1=s2 C.s1<s2 D.不确定
【来源】吉林省长春外国语学校2018-2019学年高二上学期第一次月考数学试题
【答案】C
【解析】乙选手分数的平均数分别为
所以标准差分别为
因此s1<s2,选C.
填空题(每题5分,共20分)
13.某校女子篮球队7名运动员身高(单位:cm)分布的茎叶图如图,已知记录的平均身高为175 cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数字记为x,那么x的值为________.
【来源】9-3用样本估计总体(高效训练)-2019版导学教程一轮复习数学(人教版)
【答案】2
【解析】由题意,可得,即,解得.
14.某校高三年级500名学生中,血型为O型的有200人,A型的有125人,B型的有125人,AB型的有50人.为研究血型与色弱之间的关系,现用分层抽样的方法从这500名学生中抽取一个容量为60的样本,则应抽取____名血型为AB的学生.
【来源】江苏省丹阳高级中学2018届高三上学期期中考试数学试题
【答案】6
【解析】
由题意,
故 AB 型血抽:人.
15.空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良()的天数(按这个月总共30天计算)为________.
【来源】步步高高一数学暑假作业:作业7 用样本的频率分布估计总体分布
【答案】18
【解析】根据茎叶图中,可得该样本中空气质量优的天数为2,空气质量良的天数为4,
故该样本中空气质量优良的频率为,估计该地本月空气质量优良的频率为,
从而估计该地本月空气质量优良的天数为.
16.校开展“爱我南阳、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是__________.
【来源】2011年湖北省荆州中学高二上学期期末考试数学理卷
【答案】1
【解析】由题意可知,解得,所以,故选A.
三.解答题(17题10分,其余12分/题,共70分)
17.某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.
【来源】黑龙江省海林市朝鲜族中学人教版高中数学必修三同步练习:第二章 统计单元测评
【答案】(1) ; (2)分.
【解析】(1)设该班的数学测试成绩统计的人数为m,则由茎叶图及频率分布直方图第一个矩形框知,
0.008×10,得到m=25,所以频率分布直方图中[80,90)间的矩形的高为=0.016.
(2)设这次测试的平均分为,则=55×0.08+65×0.28+75×0.4+85×0.16+95×0.08=73.8,
所以,根据茎叶图和频率分布直方图估计这次测试的平均分为73.8分.
18.一微商店对某种产品每天的销售量(件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
(1)求频率分布直方图中的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
【来源】河北省枣强中学2018-2019学年高二上学期期末考试数学(文)试题
【答案】(1)0.02;(2)22.5;(3)10800元
【解析】(1)由题意可得
(2)根据已知的频率分布直方图,日销售量的平均值为
.
(3)根据频率分布直方图,日销售量超过25件(包括25件)的天数为
,可获得的奖励为900元,
依次可以估计一年内获得的礼金数为元.
19.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下:求:
(1)根据直方图可得这100名学生中体重在(56,64)的学生人数.
(2)请根据上面的频率分布直方图估计该地区17.5-18岁的男生体重.
(3)若在这100名男生中随意抽取1人,该生体重低于62的概率是多少?
【来源】四川省广元市万达中学、八二一中学2018-2019高二下学期期中考试数学(理)试题
【答案】(1)40;(2)65.2kg;(3)P=0.28
【解析】(1)根据频率直方图得,这100名学生中体重在(56,64)的学生人数为:
(人);
(2)根据频率分布直方图得,样本的平均数是:
即利用平均数来衡量该地区17.5-18岁的男生体重是65.2kg;
(3)根据频率分布直方图得,样本数据中低于62kg的频率是 ,
∴这100名男生中随意抽取1人,该生体重低于62kg的概率是.
20.如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
【来源】河南信阳市息县第一高级中学、第二高级中学、息县高中2018-2019学年高一下学期期中联考数学(文)试题
【答案】(1)20(2)17750,1962.5
【解析】(1)由题知,月收入在[1000,1500)的频率为0.0008×500=0.4,
又月收入在[1000,1500)的有4 000人,故样本容量n10000.
又月收入在[1500,2000)的频率为0.000 4×500=0.2,
月收入在[1 500,2 000)的人数为0.2×10000=2 000,
从10 000人中用分层抽样的方法抽出100人,
则月收入在[1500,2000)的这组中应抽取100×=20(人).
(2)月收入在[1000,2000)的频率为0.4+0.2=0.6>0.5,
故样本数据的中位数为1500+=1500+250=1750.
由频率分布直方图可知, 月收入在[3000,3500)的频率为
故样本数据的平均数为
21.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这 50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布图中的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在的受访职工中,随机抽取2人,求此2人评分都在 的概率.
【来源】安徽省阜阳市临泉县第一中学2016-2017学年高一下学期学科竞赛数学(文)试题
【答案】(1); (2)
【解析】(1)由频率分布直方图知,
所以.
该企业的职工对该部分评分不低于80的概率为.
(2)在的受访职工人数为,
此2人评分都在的概率为.
22.某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
【来源】2015年全国普通高等学校招生统一考试文科数学(广东卷带解析)
【答案】(1);(2),;(3).
【解析】(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:
x=0.0075,所以直方图中x的值是0.0075. ------------- 3分
(2)月平均用电量的众数是=230. ------------- 5分
因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5
得:a=224,所以月平均用电量的中位数是224. ------------ 8分
(3)月平均用电量为[220,240]的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0.0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]的用户有0.0025×20×100=5户, -------------10分
抽取比例==,所以月平均用电量在[220,240)的用户中应抽取25×=5户.-- 12分
一.选择题(每题5分,共60分)
1.①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;③运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这三件事,恰当的抽样方法分别为( )
A.分层抽样,分层抽样,简单随机抽样
B.系统抽样,系统抽样,简单随机抽样
C.分层抽样,简单随机抽样,简单随机抽样
D.系统抽样,分层抽样,简单随机抽样
2.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A.90 B.75 C.60 D.45
3.某中学有高中生人,初中生人,男、女生所占的比例如下图所示.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从高中生中抽取女生人,则从初中生中抽取的男生人数是( )
A. B. C. D.
4.某影院有60排座位,每排70个座号,一次报告会坐满了听众,会后留下座号为15的所有听众60人进行座谈,这是运用了( )
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
5.甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,分别表示甲、乙两名运动员这项测试成绩的平均数,分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
A.
B.
C.
D.
6.(2016 浦东新区一模)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x﹣y|的值为( )
A.1 B.2 C.3 D.4
7.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是( )
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
8.某厂家生产甲、乙、丙三种不同类型的饮品 产量之比为2:3:4.为检验该厂家产品质量,用分层抽样的方法抽取一个容量为72的样本,则样本中乙类型饮品的数量为
A.16 B.24 C.32 D.48
9.某校高一年级某班共有名学生,现采用系统抽样的方法从中抽取名学生做“跑操与健康”的调查,为此将学生编号为,选取的这名学生的编号可能是( )
A. B.
C. D.
10.将参加数学竞赛决赛的名同学编号为,采用系统抽样的方法抽取一个容量为的样本,且随机抽到的号码为,这名同学分别在三个考试点考试,从到在第一考点,从到在第二考点,从到在第三考点,则第二考点被抽中的人数为( )
A. B. C. D.
11.一个蜂巢里有1只蜜蜂,第一天,它飞出去带回了5个伙伴;第二天,6只蜜蜂飞出去各自带回了5个伙伴........如果这个过程继续下去,那么第6天所有的蜜蜂归巢后,蜂巢中共有蜜蜂多少只( )
A. B. C. D.
12.甲、乙两名选手参加歌手大赛时,5名评委打的分数用如图所示的茎叶图表示,s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ).
A.s1>s2 B.s1=s2 C.s1<s2 D.不确定
填空题(每题5分,共20分)
13.某校女子篮球队7名运动员身高(单位:cm)分布的茎叶图如图,已知记录的平均身高为175 cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数字记为x,那么x的值为________.
14.某校高三年级500名学生中,血型为O型的有200人,A型的有125人,B型的有125人,AB型的有50人.为研究血型与色弱之间的关系,现用分层抽样的方法从这500名学生中抽取一个容量为60的样本,则应抽取____名血型为AB的学生.
15.空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良()的天数(按这个月总共30天计算)为________.
16.校开展“爱我南阳、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是__________.
三.解答题(17题10分,其余12分/题,共70分)
17.某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.
18.一微商店对某种产品每天的销售量(件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
(1)求频率分布直方图中的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
19.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下:求:
(1)根据直方图可得这100名学生中体重在(56,64)的学生人数.
(2)请根据上面的频率分布直方图估计该地区17.5-18岁的男生体重.
(3)若在这100名男生中随意抽取1人,该生体重低于62的概率是多少?
20.如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
21.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这 50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布图中的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在的受访职工中,随机抽取2人,求此2人评分都在 的概率.
22.某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
第九章统计测试答案
一.选择题(每题5分,共60分)
1.①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;③运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这三件事,恰当的抽样方法分别为( )
A.分层抽样,分层抽样,简单随机抽样
B.系统抽样,系统抽样,简单随机抽样
C.分层抽样,简单随机抽样,简单随机抽样
D.系统抽样,分层抽样,简单随机抽样
【来源】沈阳市2016-2017学年度(下)部分市级重点高中协作校期中测试高一数学试题
【答案】D
【解析】
①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查,此项调查的总体数目较多,而且差异不大,符合系统抽样的适用范围.
②一次数学月考中,某班有10人在100分以上,32人在90 100分,12人低于90分,现从中抽取9人了解有关情况,此项抽查的总体数目较多,而且差异很大,符合分层抽样的适用范围.
③运动会工作人员为参加4×100m接力赛的6支队伍安排跑道,此项抽查,的总体个数不多,而且差异不大,符合简单随机抽样的适用范围.
本题选择D选项.
2.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A.90 B.75 C.60 D.45
【答案】A
【解析】样本中产品净重小于100克的频率为(0.050+0.100)×2=0.3,频数为36,
∴样本总数为.
∵样本中净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.75,
∴样本中净重大于或等于98克并且小于104克的产品的个数为120×0.75=90.
3.某中学有高中生人,初中生人,男、女生所占的比例如下图所示.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从高中生中抽取女生人,则从初中生中抽取的男生人数是( )
A. B. C. D.
【来源】河南省信阳高级中学2019届高三第一次大考数学(文)试题
【答案】A
【解析】
分析:首先确定分层抽样的抽取比例,然后求解初中生中抽取的男生人数即可.
详解:因为分层抽样的抽取比例为,
所以初中生中抽取的男生人数是人.
本题选择A选项.
4.某影院有60排座位,每排70个座号,一次报告会坐满了听众,会后留下座号为15的所有听众60人进行座谈,这是运用了( )
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
【来源】陕西省黄陵中学2016-2017学年高一(普通班)下学期期末考试数学试题
【答案】C
【解析】∵听众人数比较多,
∵把每排听众从1到70号编排,
要求每班编号为15的同学留下进行交流,
这样选出的样本是采用系统抽样的方法,
故选C.
5.甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,分别表示甲、乙两名运动员这项测试成绩的平均数,分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
A.
B.
C.
D.
【来源】2018年春人教A版高中数学必修三单元测试:第二章 统计
【答案】D
【解析】
由甲、乙两名运动员在某项测试中的6次成绩的茎叶图可得,
=15,=15,
×[(-6)2+(-1)2+02+02+12+62]=×[(-7)2+(-2)2+02+02+22+72]=.
所以 .选D.
6.(2016 浦东新区一模)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x﹣y|的值为( )
A.1 B.2 C.3 D.4
【来源】2015-2016学年云南省景洪市三中高二上学期期中考试数学试卷(带解析)
【答案】D
【解析】由题意这组数据的平均数为10,方差为2可得:x+y=20,(x﹣10)2+(y﹣10)2=8,
解这个方程组需要用一些技巧,
因为不要直接求出x、y,只要求出|x﹣y|,
设x=10+t,y=10﹣t,由(x﹣10)2+(y﹣10)2=8得t2=4;
∴|x﹣y|=2|t|=4,
故选D.
7.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是( )
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
【来源】山东省济南市2019届高三5月学习质量针对性检测理科数学试题
【答案】C
【解析】由图表可知:
对于选项A中,2018年4月份我国新能源汽车的销量为8.2万辆,产量为8.1万辆,所以是正确的;
对于选项B中,2017年3月份我国新能源汽车的产量为万辆,所以是正确的;
对于选项C中,2019年2月份我国插电混合动力汽车的销量为万辆,所以不正确;
对于D中,2017年我国新能源汽车总销量为万辆,所以是正确的,
故选C.
8.某厂家生产甲、乙、丙三种不同类型的饮品 产量之比为2:3:4.为检验该厂家产品质量,用分层抽样的方法抽取一个容量为72的样本,则样本中乙类型饮品的数量为( )
A.16 B.24 C.32 D.48
【来源】河南省洛阳市2018-2019学年高一下学期期末数学试题
【答案】B
【解析】因为分层抽样总体和各层的抽样比例相同,
所以各层在总体的比例与在样本的比例相同,
所以样本中乙类型饮品的数量为.
故选B.
9.某校高一年级某班共有名学生,现采用系统抽样的方法从中抽取名学生做“跑操与健康”的调查,为此将学生编号为,选取的这名学生的编号可能是( )
A. B.
C. D.
【来源】2013届河北省石家庄市高中毕业班第一次模拟考试文科数学试卷A(带解析)
【答案】B
【解析】根据系统抽样的定义,从60名学生中抽取6名学生,编号的间隔为
∴编号组成的数列应是公差为10的等差数列,故选B.
10.将参加数学竞赛决赛的名同学编号为,采用系统抽样的方法抽取一个容量为的样本,且随机抽到的号码为,这名同学分别在三个考试点考试,从到在第一考点,从到在第二考点,从到在第三考点,则第二考点被抽中的人数为( )
A. B. C. D.
【来源】江西省新八校2019届高三第二次联考文科数学试题
【答案】C
【解析】系统抽样的分段间隔为,在随机抽样中,首次抽到号,以后每隔个号抽到一个人,则,在至号中共有17人被抽中,其编号分别为.
故选C
11.一个蜂巢里有1只蜜蜂,第一天,它飞出去带回了5个伙伴;第二天,6只蜜蜂飞出去各自带回了5个伙伴........如果这个过程继续下去,那么第6天所有的蜜蜂归巢后,蜂巢中共有蜜蜂多少只( )
A. B. C. D.
【来源】陕西省渭南市尚德中学2017-2018学年高二第一次教学质量检测数学试卷
【答案】B
【解析】第一天归巢后共有6个,第二天归巢后,共有,第三天归巢后,共有,以此类推,第六天归巢后,共有,故选B.
12.甲、乙两名选手参加歌手大赛时,5名评委打的分数用如图所示的茎叶图表示,s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ).
A.s1>s2 B.s1=s2 C.s1<s2 D.不确定
【来源】吉林省长春外国语学校2018-2019学年高二上学期第一次月考数学试题
【答案】C
【解析】乙选手分数的平均数分别为
所以标准差分别为
因此s1<s2,选C.
填空题(每题5分,共20分)
13.某校女子篮球队7名运动员身高(单位:cm)分布的茎叶图如图,已知记录的平均身高为175 cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数字记为x,那么x的值为________.
【来源】9-3用样本估计总体(高效训练)-2019版导学教程一轮复习数学(人教版)
【答案】2
【解析】由题意,可得,即,解得.
14.某校高三年级500名学生中,血型为O型的有200人,A型的有125人,B型的有125人,AB型的有50人.为研究血型与色弱之间的关系,现用分层抽样的方法从这500名学生中抽取一个容量为60的样本,则应抽取____名血型为AB的学生.
【来源】江苏省丹阳高级中学2018届高三上学期期中考试数学试题
【答案】6
【解析】
由题意,
故 AB 型血抽:人.
15.空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良()的天数(按这个月总共30天计算)为________.
【来源】步步高高一数学暑假作业:作业7 用样本的频率分布估计总体分布
【答案】18
【解析】根据茎叶图中,可得该样本中空气质量优的天数为2,空气质量良的天数为4,
故该样本中空气质量优良的频率为,估计该地本月空气质量优良的频率为,
从而估计该地本月空气质量优良的天数为.
16.校开展“爱我南阳、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是__________.
【来源】2011年湖北省荆州中学高二上学期期末考试数学理卷
【答案】1
【解析】由题意可知,解得,所以,故选A.
三.解答题(17题10分,其余12分/题,共70分)
17.某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.
【来源】黑龙江省海林市朝鲜族中学人教版高中数学必修三同步练习:第二章 统计单元测评
【答案】(1) ; (2)分.
【解析】(1)设该班的数学测试成绩统计的人数为m,则由茎叶图及频率分布直方图第一个矩形框知,
0.008×10,得到m=25,所以频率分布直方图中[80,90)间的矩形的高为=0.016.
(2)设这次测试的平均分为,则=55×0.08+65×0.28+75×0.4+85×0.16+95×0.08=73.8,
所以,根据茎叶图和频率分布直方图估计这次测试的平均分为73.8分.
18.一微商店对某种产品每天的销售量(件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
(1)求频率分布直方图中的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
【来源】河北省枣强中学2018-2019学年高二上学期期末考试数学(文)试题
【答案】(1)0.02;(2)22.5;(3)10800元
【解析】(1)由题意可得
(2)根据已知的频率分布直方图,日销售量的平均值为
.
(3)根据频率分布直方图,日销售量超过25件(包括25件)的天数为
,可获得的奖励为900元,
依次可以估计一年内获得的礼金数为元.
19.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下:求:
(1)根据直方图可得这100名学生中体重在(56,64)的学生人数.
(2)请根据上面的频率分布直方图估计该地区17.5-18岁的男生体重.
(3)若在这100名男生中随意抽取1人,该生体重低于62的概率是多少?
【来源】四川省广元市万达中学、八二一中学2018-2019高二下学期期中考试数学(理)试题
【答案】(1)40;(2)65.2kg;(3)P=0.28
【解析】(1)根据频率直方图得,这100名学生中体重在(56,64)的学生人数为:
(人);
(2)根据频率分布直方图得,样本的平均数是:
即利用平均数来衡量该地区17.5-18岁的男生体重是65.2kg;
(3)根据频率分布直方图得,样本数据中低于62kg的频率是 ,
∴这100名男生中随意抽取1人,该生体重低于62kg的概率是.
20.如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
【来源】河南信阳市息县第一高级中学、第二高级中学、息县高中2018-2019学年高一下学期期中联考数学(文)试题
【答案】(1)20(2)17750,1962.5
【解析】(1)由题知,月收入在[1000,1500)的频率为0.0008×500=0.4,
又月收入在[1000,1500)的有4 000人,故样本容量n10000.
又月收入在[1500,2000)的频率为0.000 4×500=0.2,
月收入在[1 500,2 000)的人数为0.2×10000=2 000,
从10 000人中用分层抽样的方法抽出100人,
则月收入在[1500,2000)的这组中应抽取100×=20(人).
(2)月收入在[1000,2000)的频率为0.4+0.2=0.6>0.5,
故样本数据的中位数为1500+=1500+250=1750.
由频率分布直方图可知, 月收入在[3000,3500)的频率为
故样本数据的平均数为
21.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这 50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布图中的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在的受访职工中,随机抽取2人,求此2人评分都在 的概率.
【来源】安徽省阜阳市临泉县第一中学2016-2017学年高一下学期学科竞赛数学(文)试题
【答案】(1); (2)
【解析】(1)由频率分布直方图知,
所以.
该企业的职工对该部分评分不低于80的概率为.
(2)在的受访职工人数为,
此2人评分都在的概率为.
22.某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图.
(1)求直方图中的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,,,的四组用户中,用分层抽样的方法抽取户居民,则月平均用电量在的用户中应抽取多少户?
【来源】2015年全国普通高等学校招生统一考试文科数学(广东卷带解析)
【答案】(1);(2),;(3).
【解析】(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:
x=0.0075,所以直方图中x的值是0.0075. ------------- 3分
(2)月平均用电量的众数是=230. ------------- 5分
因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5
得:a=224,所以月平均用电量的中位数是224. ------------ 8分
(3)月平均用电量为[220,240]的用户有0.0125×20×100=25户,
月平均用电量为[240,260)的用户有0.0075×20×100=15户,
月平均用电量为[260,280)的用户有0. 005×20×100=10户,
月平均用电量为[280,300]的用户有0.0025×20×100=5户, -------------10分
抽取比例==,所以月平均用电量在[220,240)的用户中应抽取25×=5户.-- 12分
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
