1.1.1锐角三角形函数 学案
图片预览

文档简介
中小学教育资源及组卷应用平台
1.1.1锐角三角形函数 导学案
课题 1.1.1锐角三角形函数 单元 第1单元 学科 数学 年级 九年级(下)
教材分析 理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。了解计算一个锐角的正切值的过程、方法;逐步培养学生分析问题、解决问题的能力。
核心素养分析 1.通过解答实际问题,激发学生学数学的兴趣,增长社会见识。2.使学生亲身经历用正切函数计算坡度的过程,感受数学实用性,培养学生积极情感。3.领会教学活动中的类比思想,提高学生学习数学的积极性。
学习目标 1.理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值;2.能够根据正切的概念进行简单的计算;3.能运用正切、坡度解决问题。
重点 理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。
难点 能运用正切、坡度解决问题。
教学过程
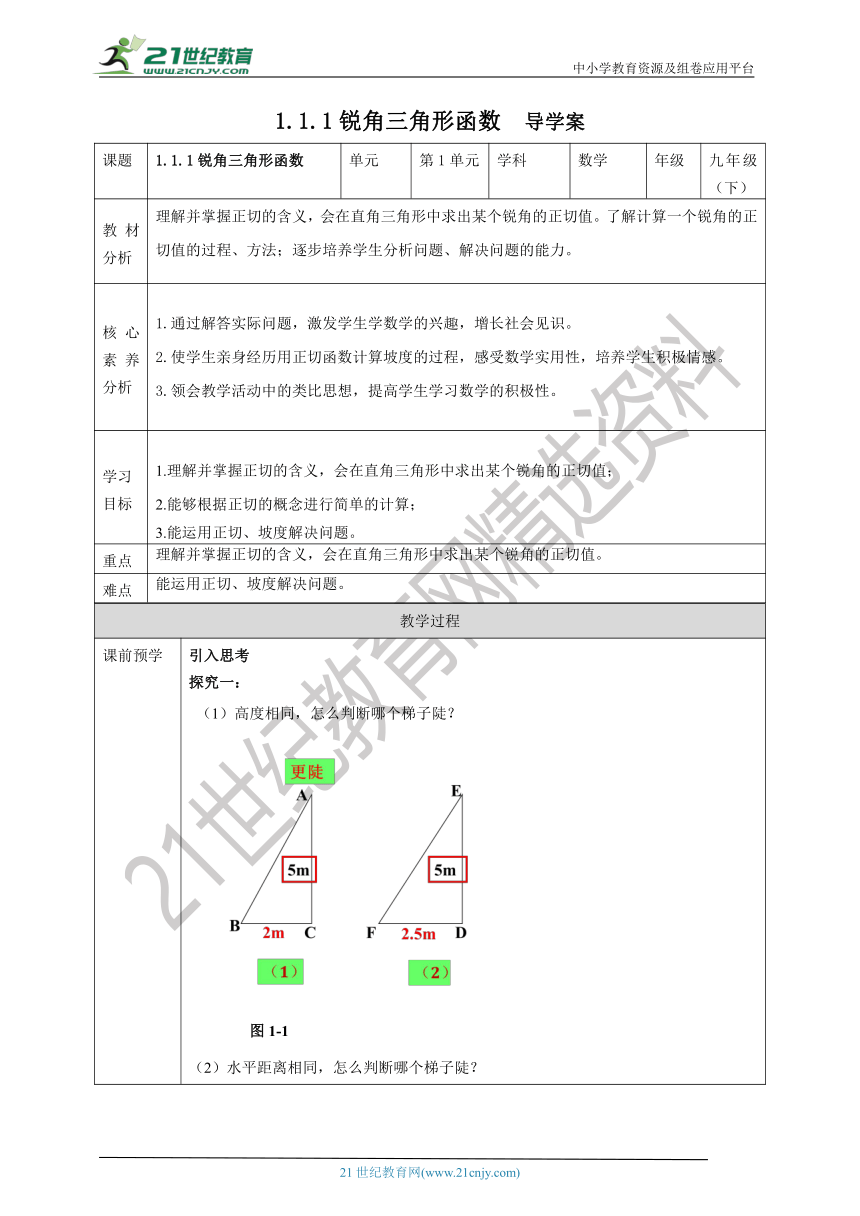
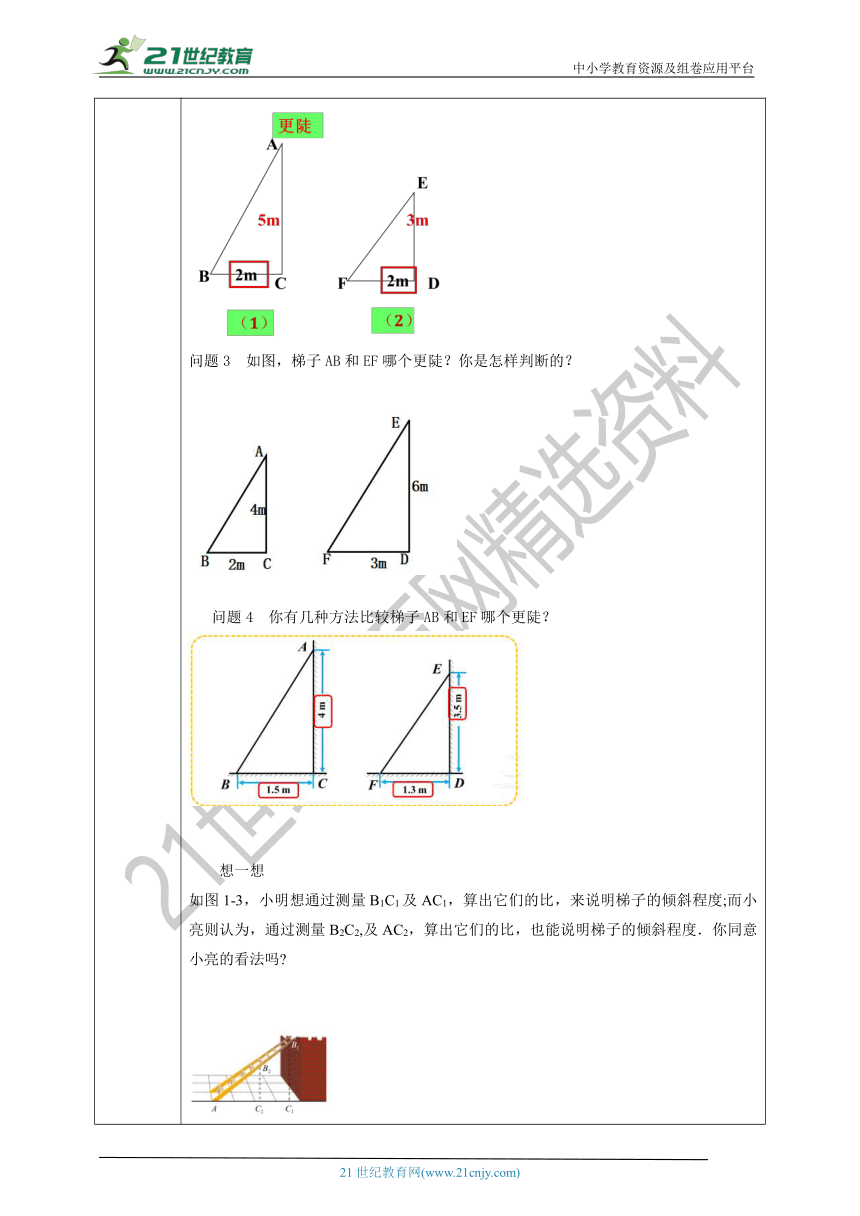
课前预学 引入思考探究一: (1)高度相同,怎么判断哪个梯子陡? 图1-1(2)水平距离相同,怎么判断哪个梯子陡?问题3 如图,梯子AB和EF哪个更陡?你是怎样判断的? 问题4 你有几种方法比较梯子AB和EF哪个更陡? 想一想如图1-3,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2,及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗 图1-3(1)直角三角形AB1C1和直角三角形AB2C2有什么关系 (2) 和 有什么关系 (3)如果改变B2在梯子上的位置呢 由此你能得出什么结论 探究二: 如图1-4,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切( tangent ),记作tan A,即当锐角A变化时,tan A的值也随之变化.议一议在图1-3中,梯子的倾斜程度与tanA有关系吗 tan A的值越大,梯子越陡.
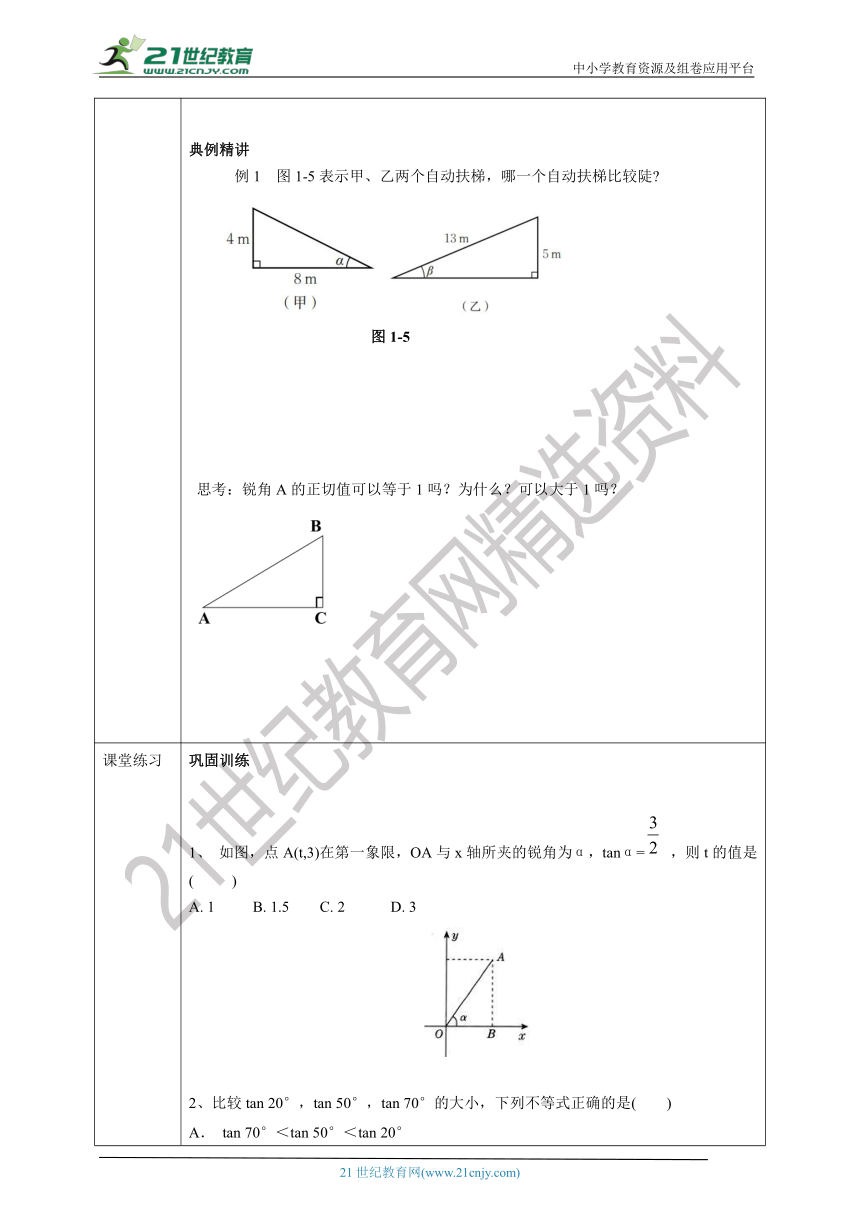
新知讲解 提炼概念注意:1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角. 2)tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”.但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1. 3)tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比.4)tanA不表示“tan”乘以“A ”.5)tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。典例精讲 例1 图1-5表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡 图1-5 思考:锐角A的正切值可以等于1吗?为什么?可以大于1吗?
课堂练习 巩固训练1、 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是 ( )A. 1 B. 1.5 C. 2 D. 3 2、比较tan 20°,tan 50°,tan 70°的大小,下列不等式正确的是( )A. tan 70°<tan 50°<tan 20°B. tan 50°<tan 20°<tan 70°C. tan 20°<tan 50°<tan 70°D. tan 20°<tan 70°<tan 50°3、在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )A. 2 B. C. D. 4. 如图,在Rt△ABC中,∠C=90°, 则tan A=________.5.如图:在等腰△ABC中,AB=AC=5,BC=6.求: tanB.6.如图所示,梯形护坡石坝的斜坡AB的坡度为1∶3,坝高BC=2米,则斜坡AB的长是多少?答案引入思考探究一:(1)直角三角形AB1C1和直角三角形AB2C2相似(2)(3)改变B2在梯子上的位置,(2)中的比值仍相等探究二:解:甲梯中,乙梯中,因为tanα>tanβ,所以甲梯更陡。正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100 m就升高60m(图1-6),那么山坡的坡度就是提炼概念 典例精讲 例 解:甲梯中,tan α= 乙梯中,tanβ= ∵tanβ>tanα,∴乙梯更陡.提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.思考 解:可以等于1,此时为等腰直角三角形; 可以大于1,当锐角的对边比邻边长的时候. 对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i (即tanα)就是: 坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切. 坡度越大,坡角越大,坡面就越陡.巩固训练1、解∵点A(t,3)在第一象限,∴AB=3,OB=t.又∵tanα= ,∴t=2.故选C.2.C3.B4. 如图,在Rt△ABC中,∠C=90°, 则tan A=________.5解:6.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
1.1.1锐角三角形函数 导学案
课题 1.1.1锐角三角形函数 单元 第1单元 学科 数学 年级 九年级(下)
教材分析 理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。了解计算一个锐角的正切值的过程、方法;逐步培养学生分析问题、解决问题的能力。
核心素养分析 1.通过解答实际问题,激发学生学数学的兴趣,增长社会见识。2.使学生亲身经历用正切函数计算坡度的过程,感受数学实用性,培养学生积极情感。3.领会教学活动中的类比思想,提高学生学习数学的积极性。
学习目标 1.理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值;2.能够根据正切的概念进行简单的计算;3.能运用正切、坡度解决问题。
重点 理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。
难点 能运用正切、坡度解决问题。
教学过程
课前预学 引入思考探究一: (1)高度相同,怎么判断哪个梯子陡? 图1-1(2)水平距离相同,怎么判断哪个梯子陡?问题3 如图,梯子AB和EF哪个更陡?你是怎样判断的? 问题4 你有几种方法比较梯子AB和EF哪个更陡? 想一想如图1-3,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2,及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗 图1-3(1)直角三角形AB1C1和直角三角形AB2C2有什么关系 (2) 和 有什么关系 (3)如果改变B2在梯子上的位置呢 由此你能得出什么结论 探究二: 如图1-4,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切( tangent ),记作tan A,即当锐角A变化时,tan A的值也随之变化.议一议在图1-3中,梯子的倾斜程度与tanA有关系吗 tan A的值越大,梯子越陡.
新知讲解 提炼概念注意:1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角. 2)tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”.但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1. 3)tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比.4)tanA不表示“tan”乘以“A ”.5)tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。典例精讲 例1 图1-5表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡 图1-5 思考:锐角A的正切值可以等于1吗?为什么?可以大于1吗?
课堂练习 巩固训练1、 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是 ( )A. 1 B. 1.5 C. 2 D. 3 2、比较tan 20°,tan 50°,tan 70°的大小,下列不等式正确的是( )A. tan 70°<tan 50°<tan 20°B. tan 50°<tan 20°<tan 70°C. tan 20°<tan 50°<tan 70°D. tan 20°<tan 70°<tan 50°3、在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )A. 2 B. C. D. 4. 如图,在Rt△ABC中,∠C=90°, 则tan A=________.5.如图:在等腰△ABC中,AB=AC=5,BC=6.求: tanB.6.如图所示,梯形护坡石坝的斜坡AB的坡度为1∶3,坝高BC=2米,则斜坡AB的长是多少?答案引入思考探究一:(1)直角三角形AB1C1和直角三角形AB2C2相似(2)(3)改变B2在梯子上的位置,(2)中的比值仍相等探究二:解:甲梯中,乙梯中,因为tanα>tanβ,所以甲梯更陡。正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100 m就升高60m(图1-6),那么山坡的坡度就是提炼概念 典例精讲 例 解:甲梯中,tan α= 乙梯中,tanβ= ∵tanβ>tanα,∴乙梯更陡.提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.思考 解:可以等于1,此时为等腰直角三角形; 可以大于1,当锐角的对边比邻边长的时候. 对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i (即tanα)就是: 坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切. 坡度越大,坡角越大,坡面就越陡.巩固训练1、解∵点A(t,3)在第一象限,∴AB=3,OB=t.又∵tanα= ,∴t=2.故选C.2.C3.B4. 如图,在Rt△ABC中,∠C=90°, 则tan A=________.5解:6.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
