7.1 为什么要证明 课件 (共25张PPT)
文档属性
| 名称 | 7.1 为什么要证明 课件 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 19:12:53 | ||
图片预览







文档简介
(共25张PPT)
北师版数学八年级上册
7.1 为什么要证明
第七章 平行线的证明
1.了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.(重点)
2.会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.(难点)
现实生活中,我们常用观察的方法来了解世界.数学学习中,我们也用观察、实验、归纳的方法得出了很多结论.通过观察、度量、猜测得到的结论都是正确的吗?如果不是,那么用什么方法才能说明它的正确性呢?
感受视错觉图
“直观”可靠吗
是静还是动?
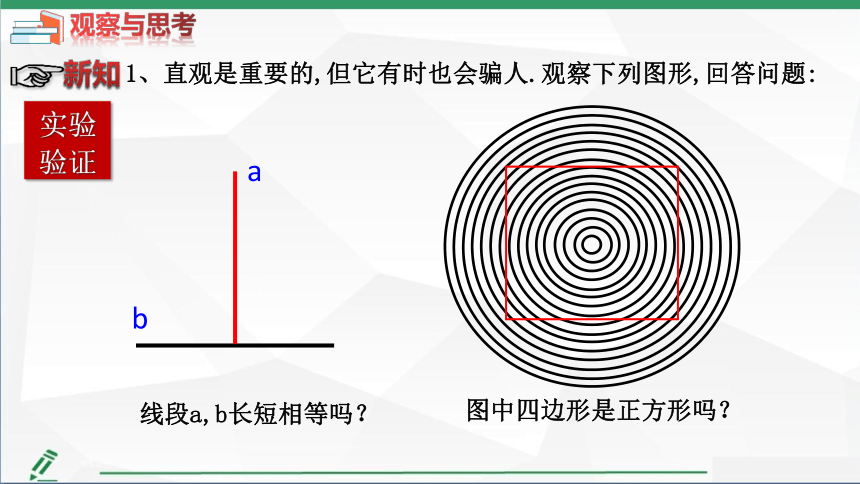
1、直观是重要的,但它有时也会骗人.观察下列图形,回答问题:
观察与思考
a
b
线段a,b长短相等吗?
图中四边形是正方形吗?
新知
实验验证
a
b
c
d
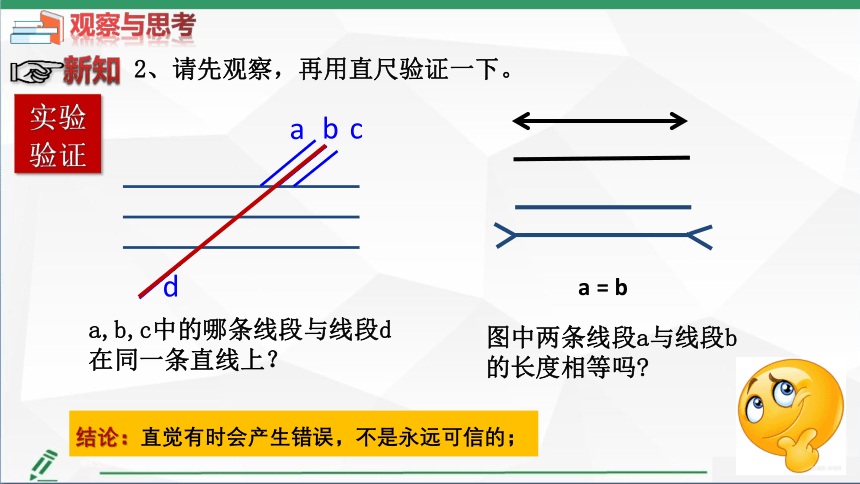
a,b,c中的哪条线段与线段d在同一条直线上?
观察与思考
新知
2、请先观察,再用直尺验证一下。
a = b
图中两条线段a与线段b的长度相等吗
结论:直觉有时会产生错误,不是永远可信的;
实验验证
3、下面图形中的线条是平行线吗?
观察与思考
新知
实验验证
4、请观察下图,两图中的中间圆大小一样吗?
结论:数学的结论必须经过严格的论证
观察与思考
新知
实验验证
所有的数学结论都可以用实验的方法来验证吗?
观察与思考
实验、观察、归纳是人们认识事物的重要手段.
例 如图,把地球看成球形,假如用一根比地球赤道长1m的铁丝将地球赤道围起来,铁丝与地球赤道之间的间隙能有多大?能放进一个拳头吗?先凭感觉想象一下,再具体算一算,看看与你的感觉是否一致,并与同伴进行交流.
典例探究
解:设地球半径是R,铁丝均匀地离开地面的高度为h,由圆的周长公式有:
赤道
铁丝
铁丝半径
赤道半径R
间隙h
铁丝与赤道的半径之差
2π(R+h)=2πR+1
2πR+2πh=2πR+1
2πh= 1
h≈0.17米=17 厘米.
∴拳头能通过.
铁丝的长=赤道的周长+1
等量关系
h=
间隙=铁丝的半径-赤道的半径
推理论证
你能否得到结论:对于所有自然数n,代数式n2-n+11的值都是质数?
n 0 1 2 3 4 5
n2 -n+11 11
11
13
17
23
31
典例探究
做一做
(1)代数式n2-n+11的值是质数吗?取n=0,1,2,3,4,5试一试.
n 6 7 8 9 10 11
n2 -n+11 41
53
67
83
101
121
继续找数值代入,验证你的结论.
当n=11时,n2-n+11的值为121=112,所以,对于所有自然数n,n2-n+11的值未必都是质数.
112
结论:少数特例的观察、测量或计算得出的结论,并不能保证一般情况下都成立;
推理论证
如图7-4,在 △ ABC中,点D,E分别是AB,AC的中点,连接DE. DE与BC有怎样的位置关系和数量关系 请你先猜一猜,再设法检验你的猜想.你能肯定你的结论对所有的 △ ABC都成立吗
结论:图形的性质并不都是通过测量得出的;往往缺乏说服力.
做一做
典例探究
位置关系:
数量关系:
你能肯定你的结论对所有的△ABC都成立吗?
量角器、直尺、三角板
解:如图.
延长DE至F,使EF=DE.连接FC.
∵DE=EF AE=EC ∠AED=∠FEC
∴△ADE≌△CFE(SAS)
∴AD=DB=FC ∠ADE=∠F
∴AD//FC AB//FC
综上可知BD//FC BD=FC
∴四边形DBCF是平行四边形.
∴DE= BC, DE//BC
结论:严格的推理,才能揭示问题的本质.
典例探究
F
//
//
//
//
/
/
/
实验、观察、归纳得到的结论可能正确,也可能不正确.因此,要判断一个数学结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的证明.
有下列三个说法:
①若α是无理数,则α2 是有理数;
②若α,β 是不相等的无理数,则αβ+α-β 是无理数;
③若α,β 是不相等的无理数,则 是无理数.
其中正确的个数是( )
A. 0 B.1 C.2 D.3
A
举出反例
典例探究
做一做
导引:紧扣题目中的条件举出反例验证结论是否正确.
解:当α =π 时,α2=π2 是无理数,所以①不对;
当α =1+ ,β =-1+ 时,则α β +α - β =3 是有理数,所以②不对;
当α =2 ,β = 时,则 = 是有理数,所以 ③不对
P163,当n为正整数时,n2+3n+1的值总是质数吗?
解:当n为1,2,3,4,5时,
n2+3n+1的值分别为5,7,19,29,41,
跟踪练习
但是当n等于6时, n2+3n+1的值为55,55是合数
∴当n为正整数时,n2+3n+1的值不总是质数。
1.下列说法正确的是( )
A.经验、观察或实验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大关系
C.对于自然数n,n2+n+37 一定是质数
D.有10个苹果,将它们放进9个筐中,则至少有一个筐中的苹果不少于2个
课堂练习
【解析】A,B显然错误;
对于C,当n=1时,n2+n+37=39=3×13,是合数,故C错误;
对于D,若每个筐中苹果都少于2个,那么最多只能放9个,至少有一个苹果无法放进筐中,所以把10个苹果放进9个筐中,至少有一个筐中的苹果不少于2个.
D
2、下列推理正确的是( )
A.弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟明年比今年长大了1岁
B.如果a>b,b>c,那么a>c
C.∠A与∠B相等,原因是它们看起来大小差不多
D.因为对顶角必然相等,所以相等的角也必是对顶角
B
课堂练习
3.下列结论中你能肯定的是( )
A.今天下雨,明天必然还下雨
B.三个连续整数的积一定能被6整除
C.小明在数学竞赛中一定能获奖
D.两张相片看起来佷像,则肯定照的是同一个人
B
4.下列判断正确的是( )
A.一个中学学校里不可能有同月同日生的同学
B.若a>b,则a2>b2
C.不论a为何值,总有a2>0
D.任何一个整数平方后的末位数字都不会是2或3
D
课堂练习
02=0,12=1,22=4,32=9,42=16,52=25,62=36,72=49,82=64,92=81,可得任何整数平方后的末位数字都不会是2或3.故D选项正确.
【解析】一个中学里可能有同月同日生的同学;
当a=-1,b=-2时,a>b,但a2<b2;
当a=0时,a2=0,A,B,C选项错误;
为什么要证明
实验验证
举出反例
推理证明
2
1
3
数学结论必须经过严格的论证
论证方法
费马数
历史上很多数学家都想找到求质数的公式,1640年,数学家费马验证了,当n=0、1、2、3、4时,
式子 的值为3、5、17、257、65537都是质数,于是他断言“对于所有的自然数n, 都是质数”由于费马在数学界的威望,在很长一段时间里,没有人怀疑这一结论的正确性,并把这类数称为费马数。
费马(1601~1665)法国
材料阅读
费马的失误
费马(1601~1665)法国
欧拉(1707-1783 )瑞士
1732年,数学家欧拉指出,当n=5时
从而否定了费马的结论。
更有意思的是,从第6个费马数开始,数学家们在费马数中再也没有发现一个新的质数,全都是合数.
有人甚至给出一个新的猜想:
当 ,费马数全都是合数!!
材料阅读
这个故事告诉我们:
1、 学习欧拉的求实精神与严谨的科学态度。
2、没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确。
3、要证明一个结论是错误的,举反例就是一种常用方法。
北师版数学八年级上册
7.1 为什么要证明
第七章 平行线的证明
1.了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.(重点)
2.会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.(难点)
现实生活中,我们常用观察的方法来了解世界.数学学习中,我们也用观察、实验、归纳的方法得出了很多结论.通过观察、度量、猜测得到的结论都是正确的吗?如果不是,那么用什么方法才能说明它的正确性呢?
感受视错觉图
“直观”可靠吗
是静还是动?
1、直观是重要的,但它有时也会骗人.观察下列图形,回答问题:
观察与思考
a
b
线段a,b长短相等吗?
图中四边形是正方形吗?
新知
实验验证
a
b
c
d
a,b,c中的哪条线段与线段d在同一条直线上?
观察与思考
新知
2、请先观察,再用直尺验证一下。
a = b
图中两条线段a与线段b的长度相等吗
结论:直觉有时会产生错误,不是永远可信的;
实验验证
3、下面图形中的线条是平行线吗?
观察与思考
新知
实验验证
4、请观察下图,两图中的中间圆大小一样吗?
结论:数学的结论必须经过严格的论证
观察与思考
新知
实验验证
所有的数学结论都可以用实验的方法来验证吗?
观察与思考
实验、观察、归纳是人们认识事物的重要手段.
例 如图,把地球看成球形,假如用一根比地球赤道长1m的铁丝将地球赤道围起来,铁丝与地球赤道之间的间隙能有多大?能放进一个拳头吗?先凭感觉想象一下,再具体算一算,看看与你的感觉是否一致,并与同伴进行交流.
典例探究
解:设地球半径是R,铁丝均匀地离开地面的高度为h,由圆的周长公式有:
赤道
铁丝
铁丝半径
赤道半径R
间隙h
铁丝与赤道的半径之差
2π(R+h)=2πR+1
2πR+2πh=2πR+1
2πh= 1
h≈0.17米=17 厘米.
∴拳头能通过.
铁丝的长=赤道的周长+1
等量关系
h=
间隙=铁丝的半径-赤道的半径
推理论证
你能否得到结论:对于所有自然数n,代数式n2-n+11的值都是质数?
n 0 1 2 3 4 5
n2 -n+11 11
11
13
17
23
31
典例探究
做一做
(1)代数式n2-n+11的值是质数吗?取n=0,1,2,3,4,5试一试.
n 6 7 8 9 10 11
n2 -n+11 41
53
67
83
101
121
继续找数值代入,验证你的结论.
当n=11时,n2-n+11的值为121=112,所以,对于所有自然数n,n2-n+11的值未必都是质数.
112
结论:少数特例的观察、测量或计算得出的结论,并不能保证一般情况下都成立;
推理论证
如图7-4,在 △ ABC中,点D,E分别是AB,AC的中点,连接DE. DE与BC有怎样的位置关系和数量关系 请你先猜一猜,再设法检验你的猜想.你能肯定你的结论对所有的 △ ABC都成立吗
结论:图形的性质并不都是通过测量得出的;往往缺乏说服力.
做一做
典例探究
位置关系:
数量关系:
你能肯定你的结论对所有的△ABC都成立吗?
量角器、直尺、三角板
解:如图.
延长DE至F,使EF=DE.连接FC.
∵DE=EF AE=EC ∠AED=∠FEC
∴△ADE≌△CFE(SAS)
∴AD=DB=FC ∠ADE=∠F
∴AD//FC AB//FC
综上可知BD//FC BD=FC
∴四边形DBCF是平行四边形.
∴DE= BC, DE//BC
结论:严格的推理,才能揭示问题的本质.
典例探究
F
//
//
//
//
/
/
/
实验、观察、归纳得到的结论可能正确,也可能不正确.因此,要判断一个数学结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的证明.
有下列三个说法:
①若α是无理数,则α2 是有理数;
②若α,β 是不相等的无理数,则αβ+α-β 是无理数;
③若α,β 是不相等的无理数,则 是无理数.
其中正确的个数是( )
A. 0 B.1 C.2 D.3
A
举出反例
典例探究
做一做
导引:紧扣题目中的条件举出反例验证结论是否正确.
解:当α =π 时,α2=π2 是无理数,所以①不对;
当α =1+ ,β =-1+ 时,则α β +α - β =3 是有理数,所以②不对;
当α =2 ,β = 时,则 = 是有理数,所以 ③不对
P163,当n为正整数时,n2+3n+1的值总是质数吗?
解:当n为1,2,3,4,5时,
n2+3n+1的值分别为5,7,19,29,41,
跟踪练习
但是当n等于6时, n2+3n+1的值为55,55是合数
∴当n为正整数时,n2+3n+1的值不总是质数。
1.下列说法正确的是( )
A.经验、观察或实验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大关系
C.对于自然数n,n2+n+37 一定是质数
D.有10个苹果,将它们放进9个筐中,则至少有一个筐中的苹果不少于2个
课堂练习
【解析】A,B显然错误;
对于C,当n=1时,n2+n+37=39=3×13,是合数,故C错误;
对于D,若每个筐中苹果都少于2个,那么最多只能放9个,至少有一个苹果无法放进筐中,所以把10个苹果放进9个筐中,至少有一个筐中的苹果不少于2个.
D
2、下列推理正确的是( )
A.弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟明年比今年长大了1岁
B.如果a>b,b>c,那么a>c
C.∠A与∠B相等,原因是它们看起来大小差不多
D.因为对顶角必然相等,所以相等的角也必是对顶角
B
课堂练习
3.下列结论中你能肯定的是( )
A.今天下雨,明天必然还下雨
B.三个连续整数的积一定能被6整除
C.小明在数学竞赛中一定能获奖
D.两张相片看起来佷像,则肯定照的是同一个人
B
4.下列判断正确的是( )
A.一个中学学校里不可能有同月同日生的同学
B.若a>b,则a2>b2
C.不论a为何值,总有a2>0
D.任何一个整数平方后的末位数字都不会是2或3
D
课堂练习
02=0,12=1,22=4,32=9,42=16,52=25,62=36,72=49,82=64,92=81,可得任何整数平方后的末位数字都不会是2或3.故D选项正确.
【解析】一个中学里可能有同月同日生的同学;
当a=-1,b=-2时,a>b,但a2<b2;
当a=0时,a2=0,A,B,C选项错误;
为什么要证明
实验验证
举出反例
推理证明
2
1
3
数学结论必须经过严格的论证
论证方法
费马数
历史上很多数学家都想找到求质数的公式,1640年,数学家费马验证了,当n=0、1、2、3、4时,
式子 的值为3、5、17、257、65537都是质数,于是他断言“对于所有的自然数n, 都是质数”由于费马在数学界的威望,在很长一段时间里,没有人怀疑这一结论的正确性,并把这类数称为费马数。
费马(1601~1665)法国
材料阅读
费马的失误
费马(1601~1665)法国
欧拉(1707-1783 )瑞士
1732年,数学家欧拉指出,当n=5时
从而否定了费马的结论。
更有意思的是,从第6个费马数开始,数学家们在费马数中再也没有发现一个新的质数,全都是合数.
有人甚至给出一个新的猜想:
当 ,费马数全都是合数!!
材料阅读
这个故事告诉我们:
1、 学习欧拉的求实精神与严谨的科学态度。
2、没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确。
3、要证明一个结论是错误的,举反例就是一种常用方法。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
