4.2.3有关线段长度的计算 课件(共25张PPT)
文档属性
| 名称 | 4.2.3有关线段长度的计算 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 930.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
人教版 七年级上册
4.2.3 线段的有关计算
课件说明
1.知道线段的性质;
教学目标
2.会根据图形进行与线段有关的运算.
教学重点:
根据图形进行与线段有关的运算.
A
B
O
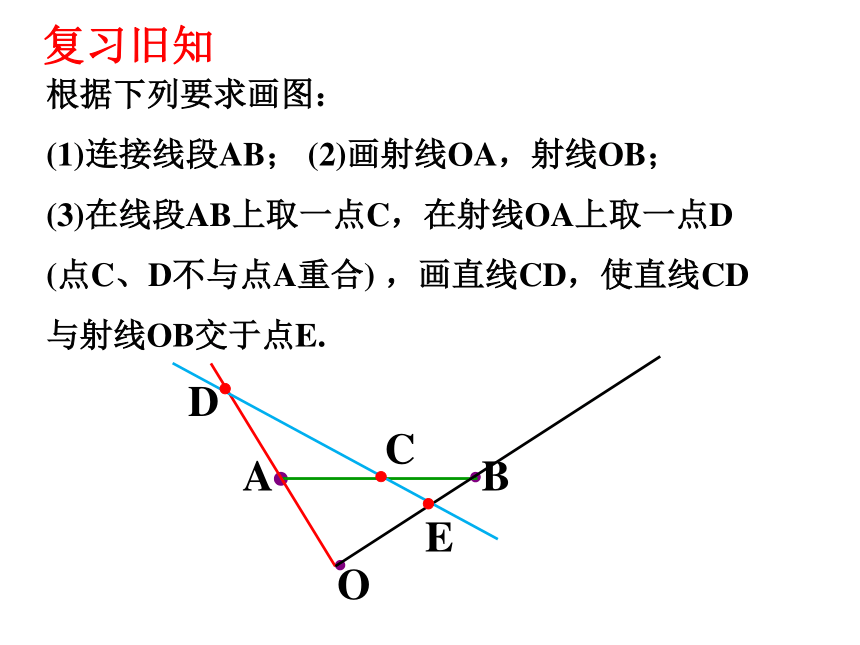
根据下列要求画图:
(1)连接线段AB; (2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D
(点C、D不与点A重合) ,画直线CD,使直线CD
与射线OB交于点E.
C
E
D
复习旧知
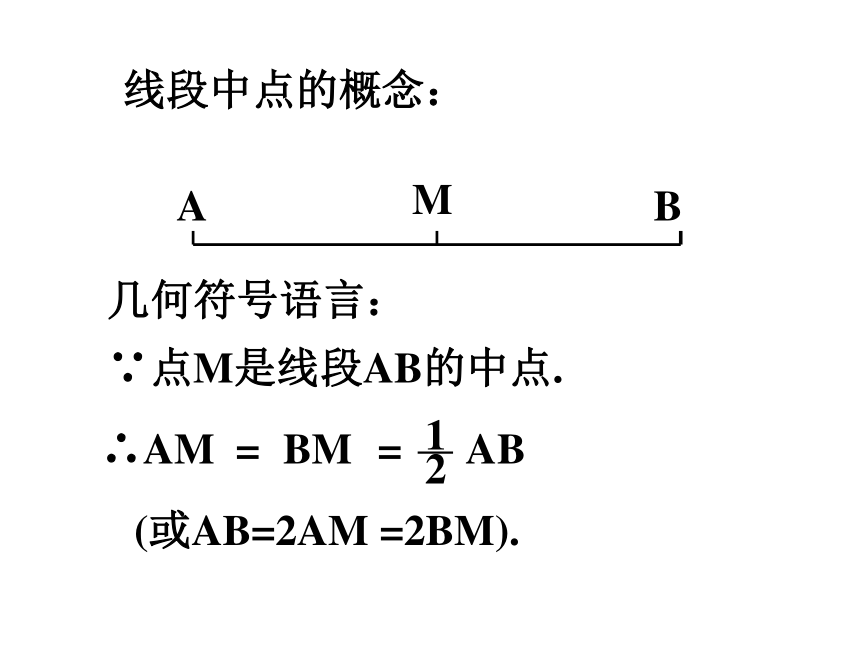
线段中点的概念:
A
B
M
∴AM
=
BM
=
-
2
1
AB
(或AB=2AM =2BM).
∵点M是线段AB的中点.
几何符号语言:
A
B
M
N
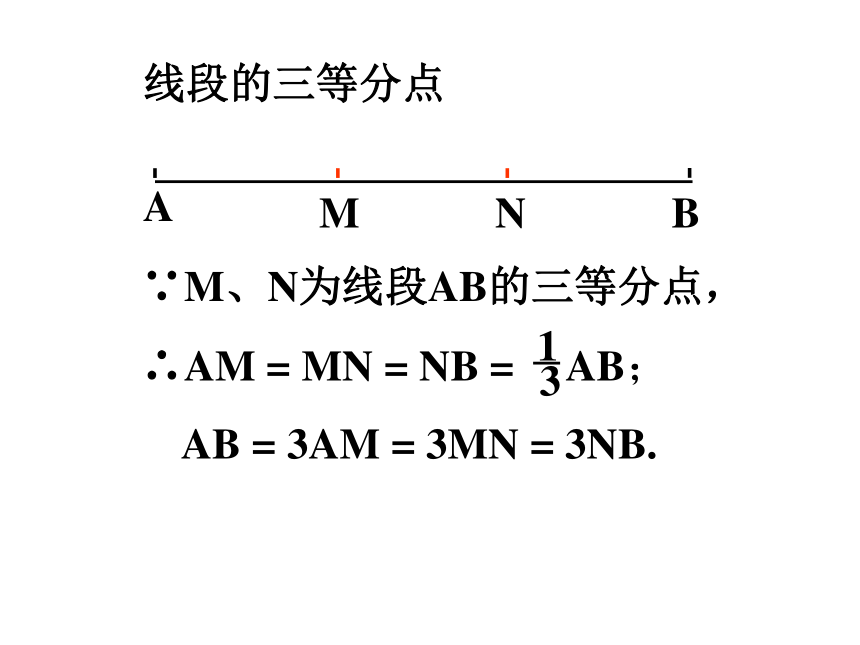
∵M、N为线段AB的三等分点,
∴AM = MN = NB = AB;
AB = 3AM = 3MN = 3NB.
1
3
线段的三等分点
A
B
M
N
P
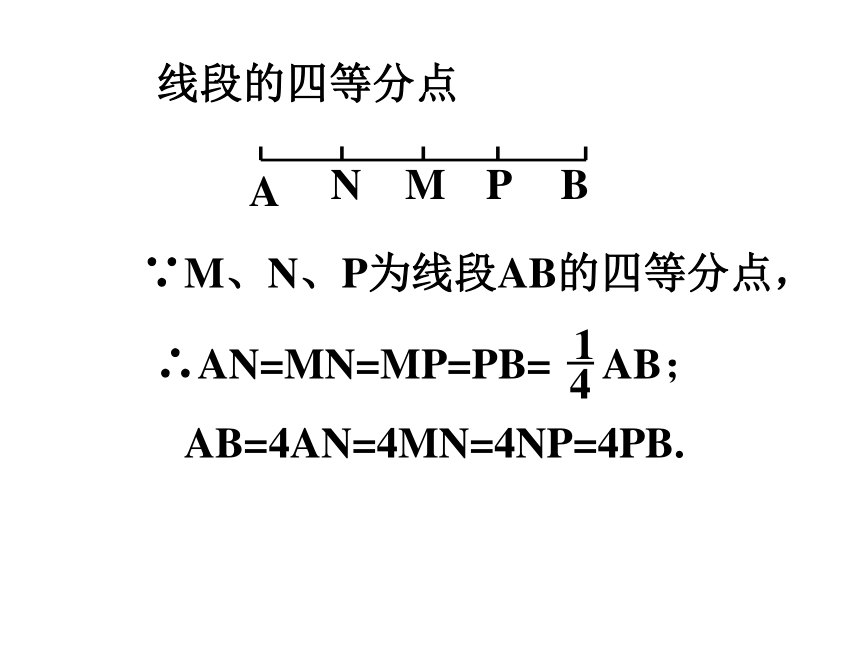
∵M、N、P为线段AB的四等分点,
∴AN=MN=MP=PB= AB;
AB=4AN=4MN=4NP=4PB.
1
4
线段的四等分点
1.M是线段AB上的一点,其中不能判定点M是线段AB中点的是( ).
A.AM+BM=AB B.AM=BM
C.AB=2BM
2.线段AB=6厘米,点C在直线AB上,
且BC=3厘米,则线段AC的长为( ).
A.3厘米 B.9厘米
C.3厘米或9厘米
A
C
D. CA= AB
1
2
D.12厘米
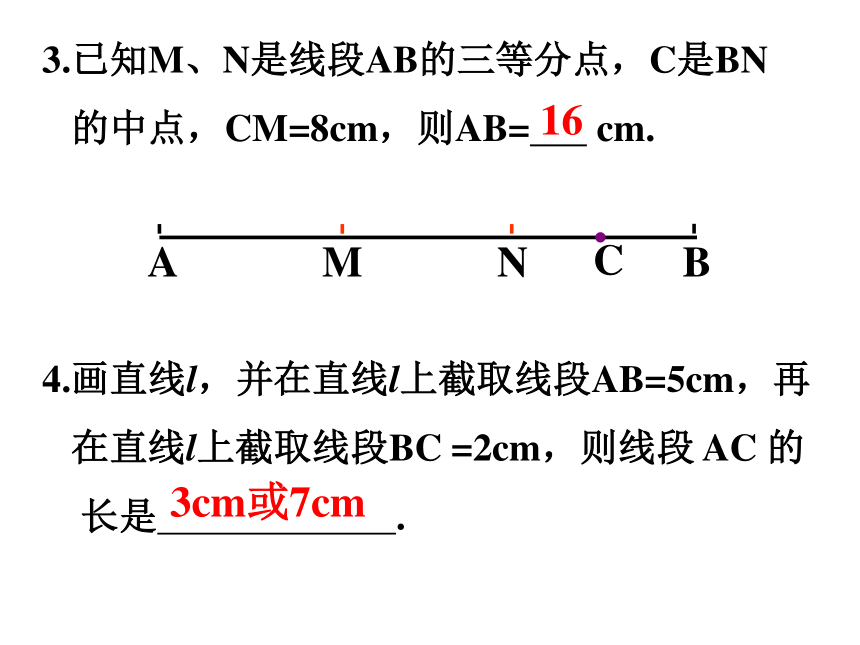
3.已知M、N是线段AB的三等分点,C是BN
的中点,CM=8cm,则AB= cm.
A
B
M
N
C
16
4.画直线l,并在直线l上截取线段AB=5cm,再
在直线l上截取线段BC =2cm,则线段 AC 的
长是 .
3cm或7cm
A
B
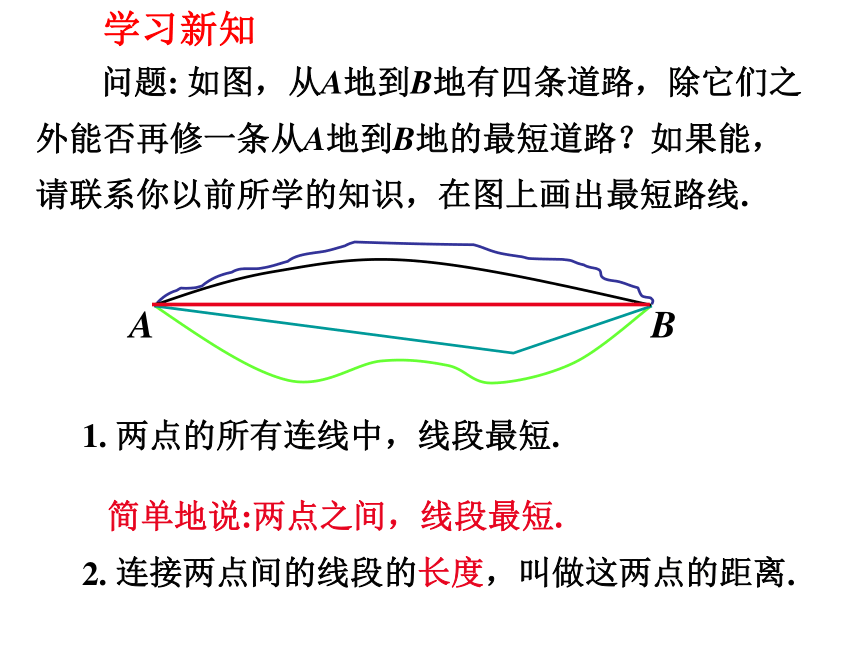
问题: 如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
1. 两点的所有连线中,线段最短.
简单地说:两点之间,线段最短.
2. 连接两点间的线段的长度,叫做这两点的距离.
学习新知
1.下列说法正确的是( ).
A.连结两点的线段叫做两点间的距离.
B.两点间的连线的长度,叫做两点间的距离.
C.连结两点的直线的长度,叫做两点的距离.
D.连结两点的线段的长度,叫做两点间的距离.
D
巩固新知
2.把弯曲的河道改直,能够缩短航程,
这样做的道理是 .
两点之间,线段最短.
3.如图,从甲地到乙地共有①、②、③、④四
条路线,其中___ (填序号)路线最短,理由
是 。
②
两点之间,线段最短.
甲
乙
②
③
①
④
分析:
例1.在直线m上顺次取A、B、C三点,使AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长.
要求
OB
要求
AO
AC
要求
由题意画图,根据线段的和、差及中点的意义去考虑.
A
B
C
m
O
例题解析
例1.在直线m上顺次取A、B、C三点,使AB=4cm,
BC=3cm,如果O是线段AC的中点,求线段OB的长.
解:
∵AB=4cm,
BC=3cm,
∴AC=
AB+BC=
=7cm.
4cm+3cm
∵O是线段AC的中点,
∴OB=
AB-AO=
4cm-3.5cm
=0.5cm
要求
OB
要求
AO
AC
要求
A
B
C
m
O
∴AO=
=3.5cm.
AB
1
2
7cm
×
=
1
2
1.已知线段AB=5cm,延长AB到C,使AC=17cm,取线段BC的中点D,求AD的长.
解:
∵AB=5cm,
AC=17cm,
∴BC=
AC-AB=
=12cm.
17cm-5cm
∵D是线段BC的中点,
∴AD=
AB+BD=
=11cm.
5cm+6cm
D
C
B
A
∴BD=
=6cm.
BC
1
2
12cm
×
=
1
2
巩固新知
A
C
D
B
2.点A、B、C 、D是直线上顺次四个点,如果AC=10cm, AB:BC:CD=2:3:4,求线段BD的长.
解:
∵AB:BC:CD=2:3:4,
设AB=2xcm,
AC=10cm,
∴BC=3xcm,
CD=4xcm,
∴BD=
BC+CD=
=14cm.
6cm+8cm
∴x=2,
AC,
∵AB+BC=
∴BC=6,
∴ 2x+3x=10,
CD=8,
(1)这节课我们学习了线段的哪个性质?
(2)线段的性质在哪些日常生活场景可看到它的应用.
课堂小结
1.下列说法中正确的个数是( ).
①过两点有且具有一条直线;
②连接两点的线段叫做两点的距离;
③两点之间线段最短;
④如果AB=BC,则点B是线段AC的中点.
A.1个 B.2个 C.3个 D.4个
B
巩固提高
2.如果线段AB=5厘米,BC=3厘米,那么A,C
两点间的距离是( ).
A.8厘米 B.2厘米 C.4厘米 D.无法确定
D
3.已知线段AB,反向延长AB到点C,使AC
= BC,D为AC中点.若CD=2cm,则AB
等于( ).
A.4cm B.6 cm C.8 cm D.10 cm
1
3
C
4.如图,小华的家在A处,书店在B处,星期日小
明到书店去买书,他想尽快地赶到书店.请你帮
助他选择一条最近的路线( ).
A.A→C→D→B
B. A→C→F→B
C. A→C→E→F→B
D. A→C→M→B
A
B
F
D
M
C
E
B
5.在数轴上有A,B,C,D四点,它们表示的
有理数分别是-4 ,3 , - ,-3 ,
则( ).
A.点C是BD的中点
B.点D是AB的中点
C.点C是AD 的中点
D.点C是AB 的中点
1
2
1
4
5
8
1
4
D
7.已知线段MN,取MN中点P,PN的中点Q,QN
的中点R,由中点的定义可知,MN = RN.
8
6.如图是电力部门进行电网改造时,都尽量 地
使电线杆排齐,根据 ;
数学的道理说明这样做可以减少电线的用量.
两点之间,线段最短
8.如图所示,AB=12,AM= AB,BN= BM,
求MN的长.
2
5
1
3
解:
∵AB=12,
∴ BM= AB-AM
∴AM=
=4.8.
AB
2
5
12
×
=
2
5
= 12-4.8=7.2
∴BN=
=2.4.
BM
1
3
7.2
×
=
1
3
∴ MN=BM-BN
= 7.2-2.4=4.8.
今天作业
课本P130习题第9、10题
课本P129习题第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
4.2.3 线段的有关计算
课件说明
1.知道线段的性质;
教学目标
2.会根据图形进行与线段有关的运算.
教学重点:
根据图形进行与线段有关的运算.
A
B
O
根据下列要求画图:
(1)连接线段AB; (2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D
(点C、D不与点A重合) ,画直线CD,使直线CD
与射线OB交于点E.
C
E
D
复习旧知
线段中点的概念:
A
B
M
∴AM
=
BM
=
-
2
1
AB
(或AB=2AM =2BM).
∵点M是线段AB的中点.
几何符号语言:
A
B
M
N
∵M、N为线段AB的三等分点,
∴AM = MN = NB = AB;
AB = 3AM = 3MN = 3NB.
1
3
线段的三等分点
A
B
M
N
P
∵M、N、P为线段AB的四等分点,
∴AN=MN=MP=PB= AB;
AB=4AN=4MN=4NP=4PB.
1
4
线段的四等分点
1.M是线段AB上的一点,其中不能判定点M是线段AB中点的是( ).
A.AM+BM=AB B.AM=BM
C.AB=2BM
2.线段AB=6厘米,点C在直线AB上,
且BC=3厘米,则线段AC的长为( ).
A.3厘米 B.9厘米
C.3厘米或9厘米
A
C
D. CA= AB
1
2
D.12厘米
3.已知M、N是线段AB的三等分点,C是BN
的中点,CM=8cm,则AB= cm.
A
B
M
N
C
16
4.画直线l,并在直线l上截取线段AB=5cm,再
在直线l上截取线段BC =2cm,则线段 AC 的
长是 .
3cm或7cm
A
B
问题: 如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
1. 两点的所有连线中,线段最短.
简单地说:两点之间,线段最短.
2. 连接两点间的线段的长度,叫做这两点的距离.
学习新知
1.下列说法正确的是( ).
A.连结两点的线段叫做两点间的距离.
B.两点间的连线的长度,叫做两点间的距离.
C.连结两点的直线的长度,叫做两点的距离.
D.连结两点的线段的长度,叫做两点间的距离.
D
巩固新知
2.把弯曲的河道改直,能够缩短航程,
这样做的道理是 .
两点之间,线段最短.
3.如图,从甲地到乙地共有①、②、③、④四
条路线,其中___ (填序号)路线最短,理由
是 。
②
两点之间,线段最短.
甲
乙
②
③
①
④
分析:
例1.在直线m上顺次取A、B、C三点,使AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长.
要求
OB
要求
AO
AC
要求
由题意画图,根据线段的和、差及中点的意义去考虑.
A
B
C
m
O
例题解析
例1.在直线m上顺次取A、B、C三点,使AB=4cm,
BC=3cm,如果O是线段AC的中点,求线段OB的长.
解:
∵AB=4cm,
BC=3cm,
∴AC=
AB+BC=
=7cm.
4cm+3cm
∵O是线段AC的中点,
∴OB=
AB-AO=
4cm-3.5cm
=0.5cm
要求
OB
要求
AO
AC
要求
A
B
C
m
O
∴AO=
=3.5cm.
AB
1
2
7cm
×
=
1
2
1.已知线段AB=5cm,延长AB到C,使AC=17cm,取线段BC的中点D,求AD的长.
解:
∵AB=5cm,
AC=17cm,
∴BC=
AC-AB=
=12cm.
17cm-5cm
∵D是线段BC的中点,
∴AD=
AB+BD=
=11cm.
5cm+6cm
D
C
B
A
∴BD=
=6cm.
BC
1
2
12cm
×
=
1
2
巩固新知
A
C
D
B
2.点A、B、C 、D是直线上顺次四个点,如果AC=10cm, AB:BC:CD=2:3:4,求线段BD的长.
解:
∵AB:BC:CD=2:3:4,
设AB=2xcm,
AC=10cm,
∴BC=3xcm,
CD=4xcm,
∴BD=
BC+CD=
=14cm.
6cm+8cm
∴x=2,
AC,
∵AB+BC=
∴BC=6,
∴ 2x+3x=10,
CD=8,
(1)这节课我们学习了线段的哪个性质?
(2)线段的性质在哪些日常生活场景可看到它的应用.
课堂小结
1.下列说法中正确的个数是( ).
①过两点有且具有一条直线;
②连接两点的线段叫做两点的距离;
③两点之间线段最短;
④如果AB=BC,则点B是线段AC的中点.
A.1个 B.2个 C.3个 D.4个
B
巩固提高
2.如果线段AB=5厘米,BC=3厘米,那么A,C
两点间的距离是( ).
A.8厘米 B.2厘米 C.4厘米 D.无法确定
D
3.已知线段AB,反向延长AB到点C,使AC
= BC,D为AC中点.若CD=2cm,则AB
等于( ).
A.4cm B.6 cm C.8 cm D.10 cm
1
3
C
4.如图,小华的家在A处,书店在B处,星期日小
明到书店去买书,他想尽快地赶到书店.请你帮
助他选择一条最近的路线( ).
A.A→C→D→B
B. A→C→F→B
C. A→C→E→F→B
D. A→C→M→B
A
B
F
D
M
C
E
B
5.在数轴上有A,B,C,D四点,它们表示的
有理数分别是-4 ,3 , - ,-3 ,
则( ).
A.点C是BD的中点
B.点D是AB的中点
C.点C是AD 的中点
D.点C是AB 的中点
1
2
1
4
5
8
1
4
D
7.已知线段MN,取MN中点P,PN的中点Q,QN
的中点R,由中点的定义可知,MN = RN.
8
6.如图是电力部门进行电网改造时,都尽量 地
使电线杆排齐,根据 ;
数学的道理说明这样做可以减少电线的用量.
两点之间,线段最短
8.如图所示,AB=12,AM= AB,BN= BM,
求MN的长.
2
5
1
3
解:
∵AB=12,
∴ BM= AB-AM
∴AM=
=4.8.
AB
2
5
12
×
=
2
5
= 12-4.8=7.2
∴BN=
=2.4.
BM
1
3
7.2
×
=
1
3
∴ MN=BM-BN
= 7.2-2.4=4.8.
今天作业
课本P130习题第9、10题
课本P129习题第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
