4.3.2有关角的运算 课件(共23张PPT)
文档属性
| 名称 | 4.3.2有关角的运算 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 09:01:52 | ||
图片预览





文档简介
(共23张PPT)
人教版 七年级上册
4.3.2有关角的运算
课件说明
1.了解方向角表示方法;
教学目标
2.进一步掌握角的计算.
教学重点:
方向角的表示方法.
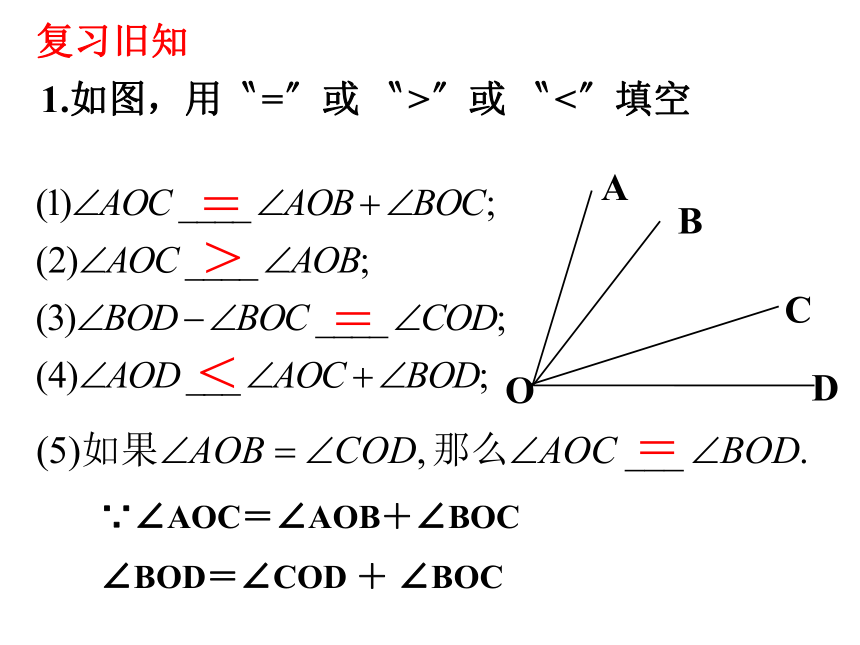
1.如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
∵∠AOC=∠AOB+∠BOC
∠BOD=∠COD + ∠BOC
复习旧知
2.计算:
109°24′
(4)
6
(3)25°36′12″
×4
(1) 34°34′+ 21°51′
(2)180°- 52°31′
=
127°29′
=
179°60′-52°31′
=
55°85′
=
56°25′
100°144′48″
=
102°24′48″
=
18°14′
=
把一个周角7等分,每一份是多少度的角?
(精确到分)
解:360°÷7=51°+3°÷7
=51°+180′÷7
≈51°26′
答:每份中的角应该是 51°26′.
例题解析
例1 如图:O是直线AB上一点,∠AOC=53°17′,
求∠BOC的度数.
解:∵∠AOB是平角=180°,
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=126°43′.
O
C
B
A
∠AOB=∠AOC+∠BOC
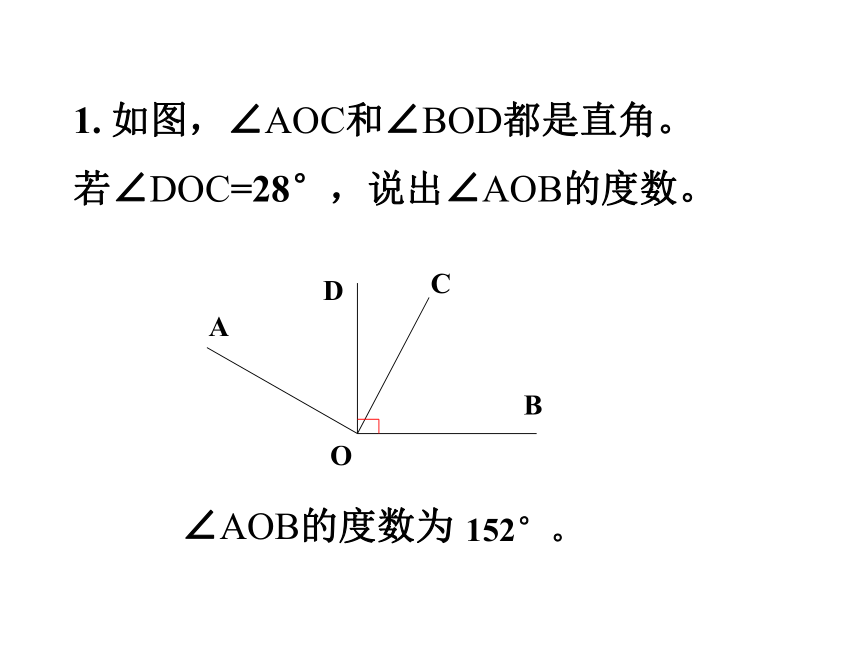
1. 如图,∠AOC和∠BOD都是直角。
若∠DOC=28°,说出∠AOB的度数。
A
B
C
D
O
152°。
∠AOB的度数为
A
B
D
C
A
B
D
C
4.如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
要求
∠BOC
要求
∠ AOC
∠ AOB
4.如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
∵OC平分∠AOD,
解:
∴∠AOC= ∠AOD
1
2
=57°
= ×114°
1
2
∵∠AOD=∠AOB+∠BOD,
∴∠AOB=38°.
∠BOD=2∠AOB,
∴3∠AOB= ∠AOD=114°,
∴∠BOC=∠AOC-∠AOB
=57°- 38°
=19°.
5.已知O为直线AB上一点,OE平分∠AOC,
OF平分∠COB,求∠EOF的大小?
A
B
E
C
F
O
解:
∵ OE平分∠ AOC,
∴∠EOC= ∠AOC,
∠COF= ∠COB.
OF平分 ∠COB,
= ∠AOC + ∠COB
= (∠AOC+∠COB)
∵∠AOB=∠AOC+∠COB=180°,
∴∠EOF=∠EOC+∠COF
1
2
1
2
1
2
1
2
1
2
= ×180°
1
2
= 90°.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:________
西南方向:________
东南方向:________
东北方向:________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
学习新知
方向角
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
甲地
乙地
乙地对甲地的方位角
先找出中心点,
然后画出方向指标
2. 把中心点和目的地
用线连接起來
3.度量向北的射线和蓝色线之间的角度
北
甲地
乙地
甲地对乙地的方位角
南
先找出中心点,
然后画出方向指标
2. 把中心点和目的地
用线连接起來
3.度量向南的射线和蓝色线之间的角度
东
西
北
南
●
A
说出B在A的
B
●
50°
70°
●
B
65°
45°
●
B
●
B
那么A在B的
●
B
40°
北偏东40°
南偏西40°
60°
东
西
北
南
O
A
例2 如图轮船O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°、南偏西10°、西北(即北偏西45°)方向上又分别发现了客轮B、货轮C、和海岛D,仿照表示灯塔方位的方法,画出表示客轮B、货轮C、和海岛D方向的射线。
·
40°
B
·
10°
C
·
45°
D
一定要正确使用量角器?
如图,A地和B地都是海上观测站,从A地发现它的北偏东60°方向有一艘船,同时,从B地发现这艘船在它北偏东30°方向,试在图中确定这艘船的位置。
A
B
东
南
西
北
东
南
西
北
·
·
C
解:如图所示,这艘船的位置在点C处。
1.谈谈本节课你有哪些收获?
2.本节课你还有哪些疑惑?
课堂小结
今天作业
课本P139习题第8题
课本P140习题第12题
课本P148习题第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
4.3.2有关角的运算
课件说明
1.了解方向角表示方法;
教学目标
2.进一步掌握角的计算.
教学重点:
方向角的表示方法.
1.如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
∵∠AOC=∠AOB+∠BOC
∠BOD=∠COD + ∠BOC
复习旧知
2.计算:
109°24′
(4)
6
(3)25°36′12″
×4
(1) 34°34′+ 21°51′
(2)180°- 52°31′
=
127°29′
=
179°60′-52°31′
=
55°85′
=
56°25′
100°144′48″
=
102°24′48″
=
18°14′
=
把一个周角7等分,每一份是多少度的角?
(精确到分)
解:360°÷7=51°+3°÷7
=51°+180′÷7
≈51°26′
答:每份中的角应该是 51°26′.
例题解析
例1 如图:O是直线AB上一点,∠AOC=53°17′,
求∠BOC的度数.
解:∵∠AOB是平角=180°,
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=126°43′.
O
C
B
A
∠AOB=∠AOC+∠BOC
1. 如图,∠AOC和∠BOD都是直角。
若∠DOC=28°,说出∠AOB的度数。
A
B
C
D
O
152°。
∠AOB的度数为
A
B
D
C
A
B
D
C
4.如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
要求
∠BOC
要求
∠ AOC
∠ AOB
4.如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
∵OC平分∠AOD,
解:
∴∠AOC= ∠AOD
1
2
=57°
= ×114°
1
2
∵∠AOD=∠AOB+∠BOD,
∴∠AOB=38°.
∠BOD=2∠AOB,
∴3∠AOB= ∠AOD=114°,
∴∠BOC=∠AOC-∠AOB
=57°- 38°
=19°.
5.已知O为直线AB上一点,OE平分∠AOC,
OF平分∠COB,求∠EOF的大小?
A
B
E
C
F
O
解:
∵ OE平分∠ AOC,
∴∠EOC= ∠AOC,
∠COF= ∠COB.
OF平分 ∠COB,
= ∠AOC + ∠COB
= (∠AOC+∠COB)
∵∠AOB=∠AOC+∠COB=180°,
∴∠EOF=∠EOC+∠COF
1
2
1
2
1
2
1
2
1
2
= ×180°
1
2
= 90°.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:________
西南方向:________
东南方向:________
东北方向:________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
学习新知
方向角
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
甲地
乙地
乙地对甲地的方位角
先找出中心点,
然后画出方向指标
2. 把中心点和目的地
用线连接起來
3.度量向北的射线和蓝色线之间的角度
北
甲地
乙地
甲地对乙地的方位角
南
先找出中心点,
然后画出方向指标
2. 把中心点和目的地
用线连接起來
3.度量向南的射线和蓝色线之间的角度
东
西
北
南
●
A
说出B在A的
B
●
50°
70°
●
B
65°
45°
●
B
●
B
那么A在B的
●
B
40°
北偏东40°
南偏西40°
60°
东
西
北
南
O
A
例2 如图轮船O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°、南偏西10°、西北(即北偏西45°)方向上又分别发现了客轮B、货轮C、和海岛D,仿照表示灯塔方位的方法,画出表示客轮B、货轮C、和海岛D方向的射线。
·
40°
B
·
10°
C
·
45°
D
一定要正确使用量角器?
如图,A地和B地都是海上观测站,从A地发现它的北偏东60°方向有一艘船,同时,从B地发现这艘船在它北偏东30°方向,试在图中确定这艘船的位置。
A
B
东
南
西
北
东
南
西
北
·
·
C
解:如图所示,这艘船的位置在点C处。
1.谈谈本节课你有哪些收获?
2.本节课你还有哪些疑惑?
课堂小结
今天作业
课本P139习题第8题
课本P140习题第12题
课本P148习题第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
