4.2.2线段长短的比较 课件(共25张PPT)
文档属性
| 名称 | 4.2.2线段长短的比较 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 09:03:36 | ||
图片预览




文档简介
(共25张PPT)
人教版 七年级上册
4.2.2 线段长短的比较
课件说明
1.知道比较线段长短的两种方法;
教学目标
2.掌握线段中点的定义.
教学重点:
线段中点的定义及表示方法.
1.读下列语句,并按这些语句画出图形:
(1)直线EF经过点F;
(2)点P在直线l外;
(3)在同一平面内,经过点O有三条直线a、b、c;
(4)线段AB、CD相交于点B.
复习旧知
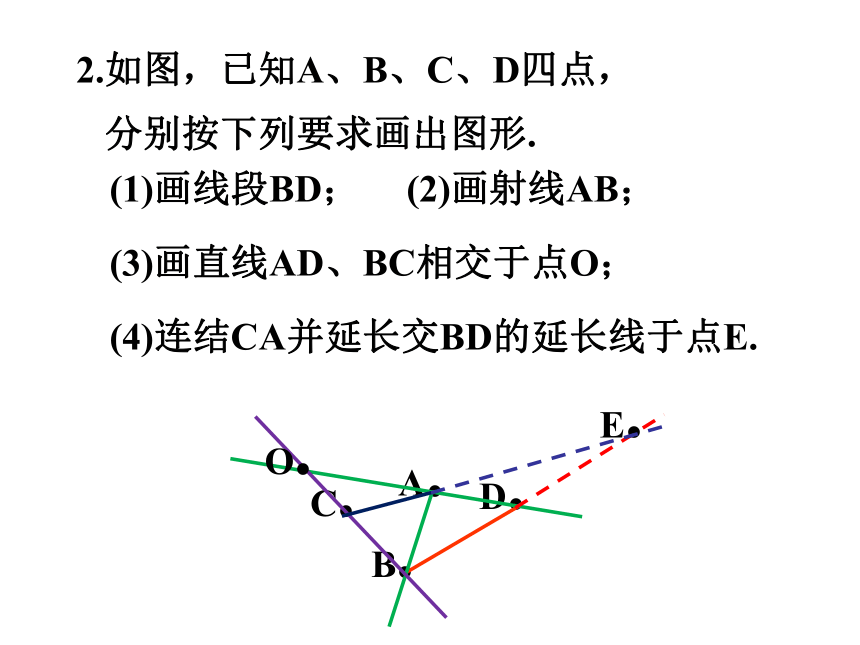
2.如图,已知A、B、C、D四点,
分别按下列要求画出图形.
A.
C.
B.
D.
O.
E.
(1)画线段BD;
(2)画射线AB;
(3)画直线AD、BC相交于点O;
(4)连结CA并延长交BD的延长线于点E.
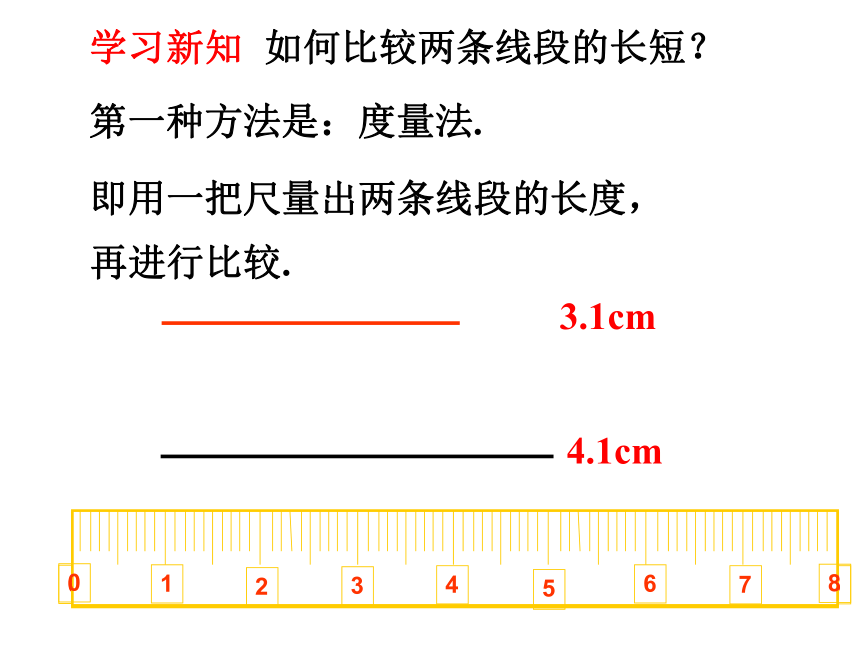
第一种方法是:度量法.
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
学习新知
如何比较两条线段的长短?
即用一把尺量出两条线段的长度,再进行比较.
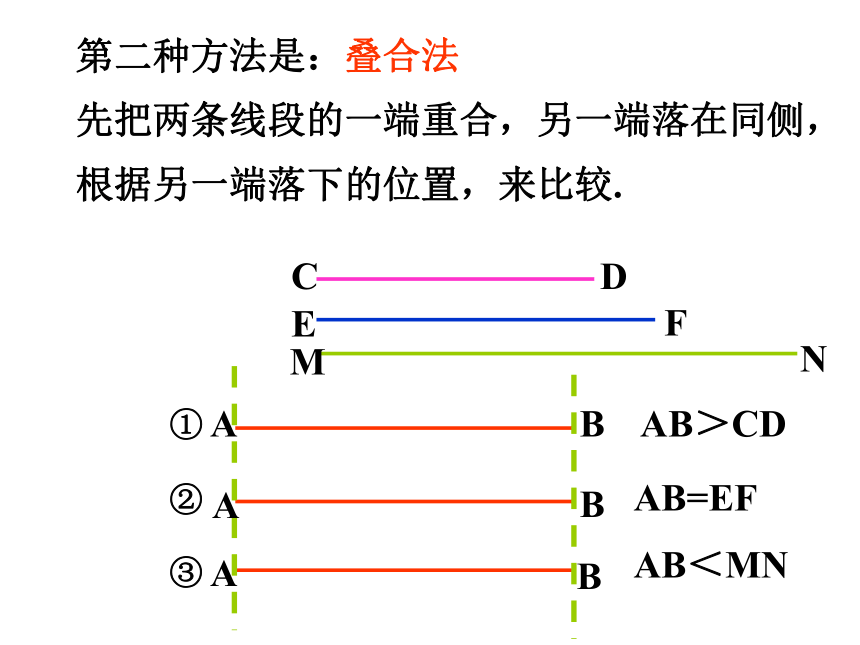
第二种方法是:叠合法
先把两条线段的一端重合,另一端落在同侧,
根据另一端落下的位置,来比较.
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
画在黑板上的两条线段是无法移动的,在没有度量工具的情况下,请大家想想办法,如何来比较它们的长短?
①
观察法
② 借助于某一物体,如铅笔、小木棒等
学习新知
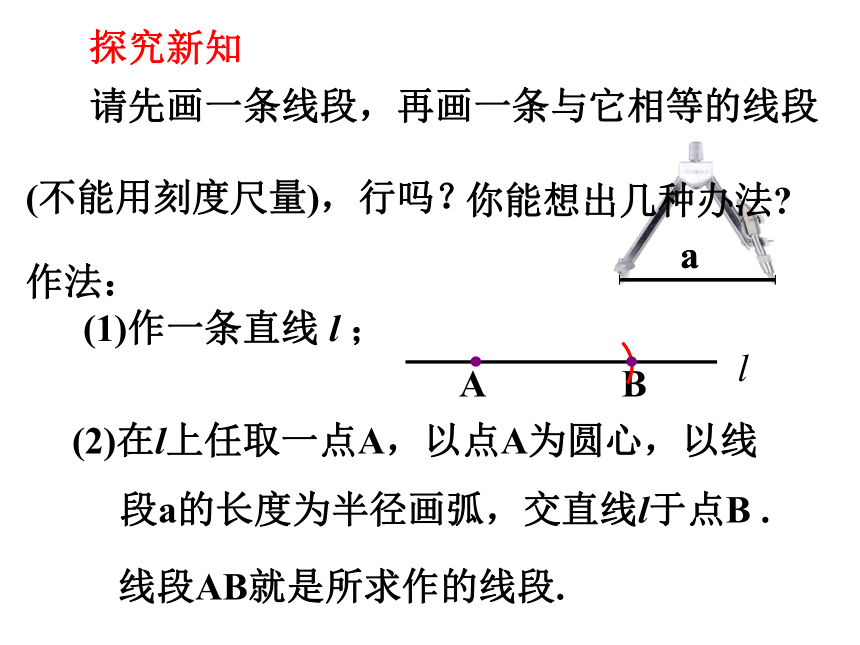
请先画一条线段,再画一条与它相等的线段
(不能用刻度尺量),行吗?
你能想出几种办法
探究新知
A
作法:
(1)作一条直线 l ;
(2)在l上任取一点A,以点A为圆心,以线
段a的长度为半径画弧,交直线l于点B .
线段AB就是所求作的线段.
B
l
a
a
b
a
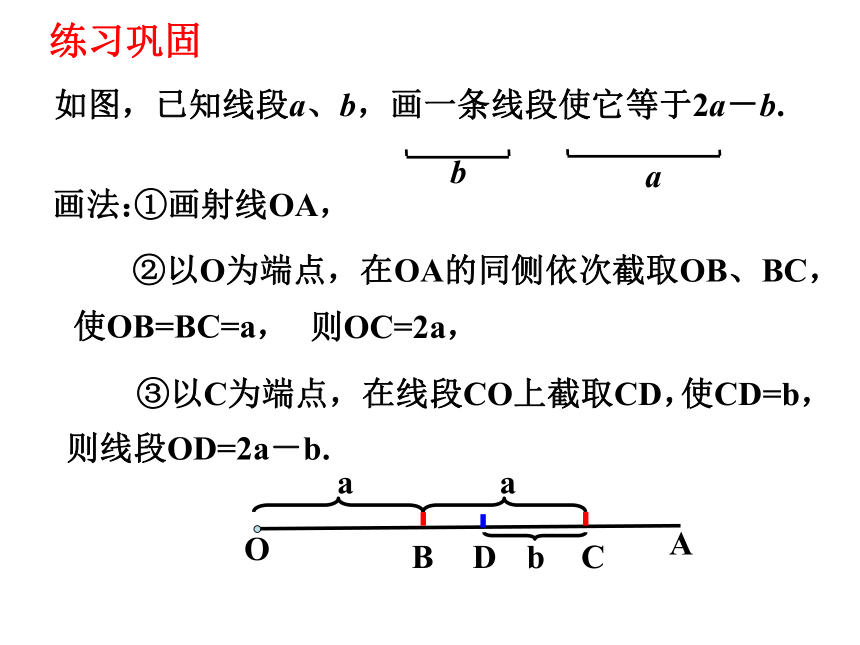
②以O为端点,在OA的同侧依次截取OB、BC,
①画射线OA,
画法:
③以C为端点,在线段CO上截取CD,
使OB=BC=a,
则OC=2a,
使CD=b,
则线段OD=2a-b.
O
A
C
B
D
b
a
a
练习巩固
如图,已知线段a、b,画一条线段使它等于2a-b.
线段中点的概念:
A
B
M
∴AM
=
BM
=
-
2
1
AB.
(或AB=2AM =2BM).
∵点M是线段AB的中点,
几何符号语言:
学习新知
自己画一条线段CD,想一想,你用什么办法找到中点M 呢?
C
D
通过折纸寻找线段中点
用尺子度量
通过折绳找到中点
探究新知
如图,点C是线段AB的中点.
(1) 若AB=6cm,则AC= cm.
(2) 若AC=6cm,则AB= cm.
3
12
练习巩固
A
B
C
典型解析
例1.如图①,AD=AB- =AC+ .
图①
BD
CD
A
C
D
B
例2 如图②,下列说法不能判断点C是线段
的中点的是( ) .
C. AC+CB=AB D. CB= AB
图②
A. AC=CB B. AB=2AC
C
1
2
A
B
C
例3.已知线段AB=4cm,在直线AB上画线段BC,
使BC=3cm,求线段AC的长.
分析:在“直线AB上画线段BC”这意味着要以B
为所画线段的一个端点,另一个端点既可
能在线段AB上,也可能在线段AB的延长
线上.
例题解析
例3.已知线段AB=4cm,在直线AB上画线段BC,
使BC=3cm,求线段AC的长.
②当端点C在线段AB的延长线上时,
①端点C在线段AB上时,
解:
AC=
AC=
AB-BC
=
4cm-3cm
=1cm
=7cm
4cm+3cm
AB+BC
=
A
B
C
A
B
C
例4.如图,点D是线段AB的中点,C是线段AD的中点,若AB=4cm,求线段CD 的长度.
解:
∵点D是线段AB的中点,
∵点C是线段AD的中点,
A
C
D
B
∴AD=
=2cm.
AB
1
2
4cm
×
=
1
2
∴CD=
=1cm.
AD
1
2
2cm
×
=
1
2
解:如图: ∵AB=BC,
∴AC=2AB,
∴点B是AC的中点.
“若AB=BC,则点B是线段AC的中点”这种说法对吗?
小聪同学的解答是这样的:
A
B
C
你认为小聪同学的解答全面吗?如果不全,漏了哪些情况?
答:不全面.漏了点B不在线段AC上这一情况.
练习巩固
(1)比较线段的长短有哪两种方法?
①度量法; ②叠合法.
(2)由线段中点的定义,可以得到哪些相等的关系式?
课堂小结
1.已知AD=4cm,BD=3cm,C为AB的中点,
求线段BC的长.
A
C
D
B
解:
∵AD=4cm,
BD=3cm,
∴AB=
AD+BD=
=7cm.
4cm+3cm
∵C是线段AB的中点,
∴BC=
=3.5cm.
AB
1
2
7cm
×
=
1
2
巩固新知
2.已知AB=9cm,BD=3cm,C为AB的中点,求线段DC的长.
A
C
D
B
解:
∵BC=4.5cm,
BD=3cm,
∴DC=
BC-BD=
=1.5cm.
4.5cm-3cm
∵C是线段AB的中点,
∴BC=
=4.5cm.
AB
1
2
9cm
×
=
1
2
3. 点C是AB延长线上的一点,点D是AB中点,如果点B 恰好是DC的中点,设AB=4cm,求线段 AC的长.
A
C
D
B
解:
∵D是线段AB的中点,
∴AD=BD =
∴AC=
AD+DC=
=6cm.
2cm+4cm
∵B是线段DC的中点,
∴DC=2BD
=
2×2cm
=4cm
=2cm.
AB
1
2
4cm
×
=
1
2
今天作业
课本P130习题第9、10题
课本P129习题第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
4.2.2 线段长短的比较
课件说明
1.知道比较线段长短的两种方法;
教学目标
2.掌握线段中点的定义.
教学重点:
线段中点的定义及表示方法.
1.读下列语句,并按这些语句画出图形:
(1)直线EF经过点F;
(2)点P在直线l外;
(3)在同一平面内,经过点O有三条直线a、b、c;
(4)线段AB、CD相交于点B.
复习旧知
2.如图,已知A、B、C、D四点,
分别按下列要求画出图形.
A.
C.
B.
D.
O.
E.
(1)画线段BD;
(2)画射线AB;
(3)画直线AD、BC相交于点O;
(4)连结CA并延长交BD的延长线于点E.
第一种方法是:度量法.
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
学习新知
如何比较两条线段的长短?
即用一把尺量出两条线段的长度,再进行比较.
第二种方法是:叠合法
先把两条线段的一端重合,另一端落在同侧,
根据另一端落下的位置,来比较.
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
画在黑板上的两条线段是无法移动的,在没有度量工具的情况下,请大家想想办法,如何来比较它们的长短?
①
观察法
② 借助于某一物体,如铅笔、小木棒等
学习新知
请先画一条线段,再画一条与它相等的线段
(不能用刻度尺量),行吗?
你能想出几种办法
探究新知
A
作法:
(1)作一条直线 l ;
(2)在l上任取一点A,以点A为圆心,以线
段a的长度为半径画弧,交直线l于点B .
线段AB就是所求作的线段.
B
l
a
a
b
a
②以O为端点,在OA的同侧依次截取OB、BC,
①画射线OA,
画法:
③以C为端点,在线段CO上截取CD,
使OB=BC=a,
则OC=2a,
使CD=b,
则线段OD=2a-b.
O
A
C
B
D
b
a
a
练习巩固
如图,已知线段a、b,画一条线段使它等于2a-b.
线段中点的概念:
A
B
M
∴AM
=
BM
=
-
2
1
AB.
(或AB=2AM =2BM).
∵点M是线段AB的中点,
几何符号语言:
学习新知
自己画一条线段CD,想一想,你用什么办法找到中点M 呢?
C
D
通过折纸寻找线段中点
用尺子度量
通过折绳找到中点
探究新知
如图,点C是线段AB的中点.
(1) 若AB=6cm,则AC= cm.
(2) 若AC=6cm,则AB= cm.
3
12
练习巩固
A
B
C
典型解析
例1.如图①,AD=AB- =AC+ .
图①
BD
CD
A
C
D
B
例2 如图②,下列说法不能判断点C是线段
的中点的是( ) .
C. AC+CB=AB D. CB= AB
图②
A. AC=CB B. AB=2AC
C
1
2
A
B
C
例3.已知线段AB=4cm,在直线AB上画线段BC,
使BC=3cm,求线段AC的长.
分析:在“直线AB上画线段BC”这意味着要以B
为所画线段的一个端点,另一个端点既可
能在线段AB上,也可能在线段AB的延长
线上.
例题解析
例3.已知线段AB=4cm,在直线AB上画线段BC,
使BC=3cm,求线段AC的长.
②当端点C在线段AB的延长线上时,
①端点C在线段AB上时,
解:
AC=
AC=
AB-BC
=
4cm-3cm
=1cm
=7cm
4cm+3cm
AB+BC
=
A
B
C
A
B
C
例4.如图,点D是线段AB的中点,C是线段AD的中点,若AB=4cm,求线段CD 的长度.
解:
∵点D是线段AB的中点,
∵点C是线段AD的中点,
A
C
D
B
∴AD=
=2cm.
AB
1
2
4cm
×
=
1
2
∴CD=
=1cm.
AD
1
2
2cm
×
=
1
2
解:如图: ∵AB=BC,
∴AC=2AB,
∴点B是AC的中点.
“若AB=BC,则点B是线段AC的中点”这种说法对吗?
小聪同学的解答是这样的:
A
B
C
你认为小聪同学的解答全面吗?如果不全,漏了哪些情况?
答:不全面.漏了点B不在线段AC上这一情况.
练习巩固
(1)比较线段的长短有哪两种方法?
①度量法; ②叠合法.
(2)由线段中点的定义,可以得到哪些相等的关系式?
课堂小结
1.已知AD=4cm,BD=3cm,C为AB的中点,
求线段BC的长.
A
C
D
B
解:
∵AD=4cm,
BD=3cm,
∴AB=
AD+BD=
=7cm.
4cm+3cm
∵C是线段AB的中点,
∴BC=
=3.5cm.
AB
1
2
7cm
×
=
1
2
巩固新知
2.已知AB=9cm,BD=3cm,C为AB的中点,求线段DC的长.
A
C
D
B
解:
∵BC=4.5cm,
BD=3cm,
∴DC=
BC-BD=
=1.5cm.
4.5cm-3cm
∵C是线段AB的中点,
∴BC=
=4.5cm.
AB
1
2
9cm
×
=
1
2
3. 点C是AB延长线上的一点,点D是AB中点,如果点B 恰好是DC的中点,设AB=4cm,求线段 AC的长.
A
C
D
B
解:
∵D是线段AB的中点,
∴AD=BD =
∴AC=
AD+DC=
=6cm.
2cm+4cm
∵B是线段DC的中点,
∴DC=2BD
=
2×2cm
=4cm
=2cm.
AB
1
2
4cm
×
=
1
2
今天作业
课本P130习题第9、10题
课本P129习题第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
