2022-2023学年京改版数学九年级上册(北京地区)第十八章 相似形 综合复习题(含解析)
文档属性
| 名称 | 2022-2023学年京改版数学九年级上册(北京地区)第十八章 相似形 综合复习题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 682.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 19:35:44 | ||
图片预览



文档简介
第十八章 相似形 综合复习题
一、单选题
1.(2022·北京房山·九年级期中)若,则下列比例式成立的是( )
A. B. C. D.
2.(2022·北京昌平·九年级期中)下列各组线段中,成比例的是( )
A.1,2,2,4 B.1,2,3,4
C.3,5,9,13 D.1,2,2,3
3.(2022·北京市顺义区仁和中学九年级期中)已知点是线段的黄金分割点,且,,则的长为( )
A. B. C. D.0.618
4.(2022·北京房山·九年级期中)如图,已知∥∥,,那么的值是( )
A. B. C. D.2
5.(2022·北京大兴·二模)如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD︰AB=3︰4,AE=6,则AC等于( )
A.3
B.4
C.6
D.8
6.(2022·北京通州·九年级期中)下列判断正确的是( )
A.任意两个平行四边形一定相似 B.任意两个矩形一定相似
C.任意两个菱形一定相似 D.任意两个正方形一定相似
7.(2022·北京市大峪中学分校九年级期中)若两个相似多边形的的相似比为,则它们面积之比为( )
A. B. C. D.
8.(2022·北京·大峪中学九年级期中)如图,是的边上一点,那么下面四个命题中错误的是( )
A.如果,那么
B.如果,那么
C.如果,那么
D.如果,那么
9.(2022·北京房山·九年级期中)如图,F是的边上一点,则下列条件不能判定与相似的是( )
A. B. C. D.
10.(2022·北京·九年级单元测试)如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
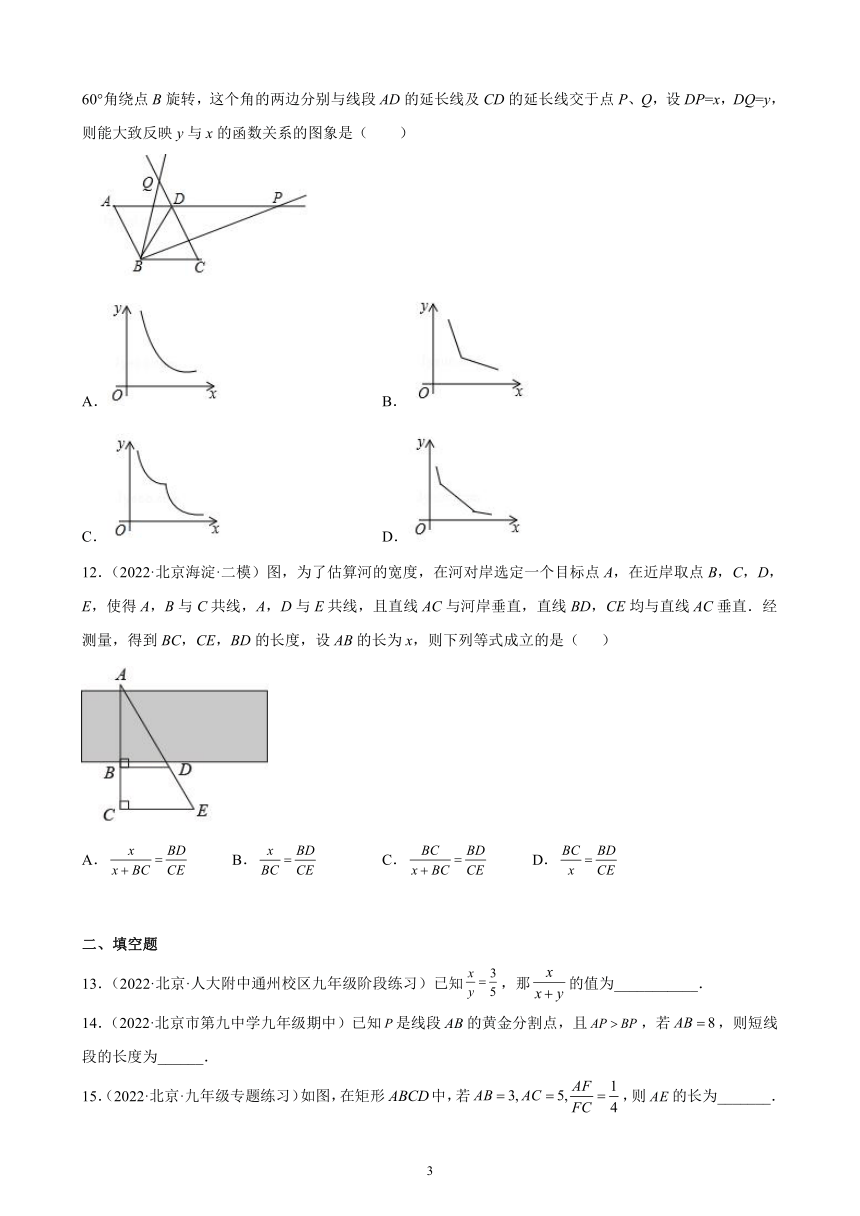
11.(2022·北京双榆树中学九年级期中)如图,菱形ABCD的边长为2,∠A=60°,一个以点B为顶点的60°角绕点B旋转,这个角的两边分别与线段AD的延长线及CD的延长线交于点P、Q,设DP=x,DQ=y,则能大致反映y与x的函数关系的图象是( )
A. B.
C. D.
12.(2022·北京海淀·二模)图,为了估算河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,E,使得A,B与C共线,A,D与E共线,且直线AC与河岸垂直,直线BD,CE均与直线AC垂直.经测量,得到BC,CE,BD的长度,设AB的长为x,则下列等式成立的是( )
A. B. C. D.
二、填空题
13.(2022·北京·人大附中通州校区九年级阶段练习)已知,那的值为___________.
14.(2022·北京市第九中学九年级期中)已知是线段的黄金分割点,且,若,则短线段的长度为______.
15.(2022·北京·九年级专题练习)如图,在矩形中,若,则的长为_______.
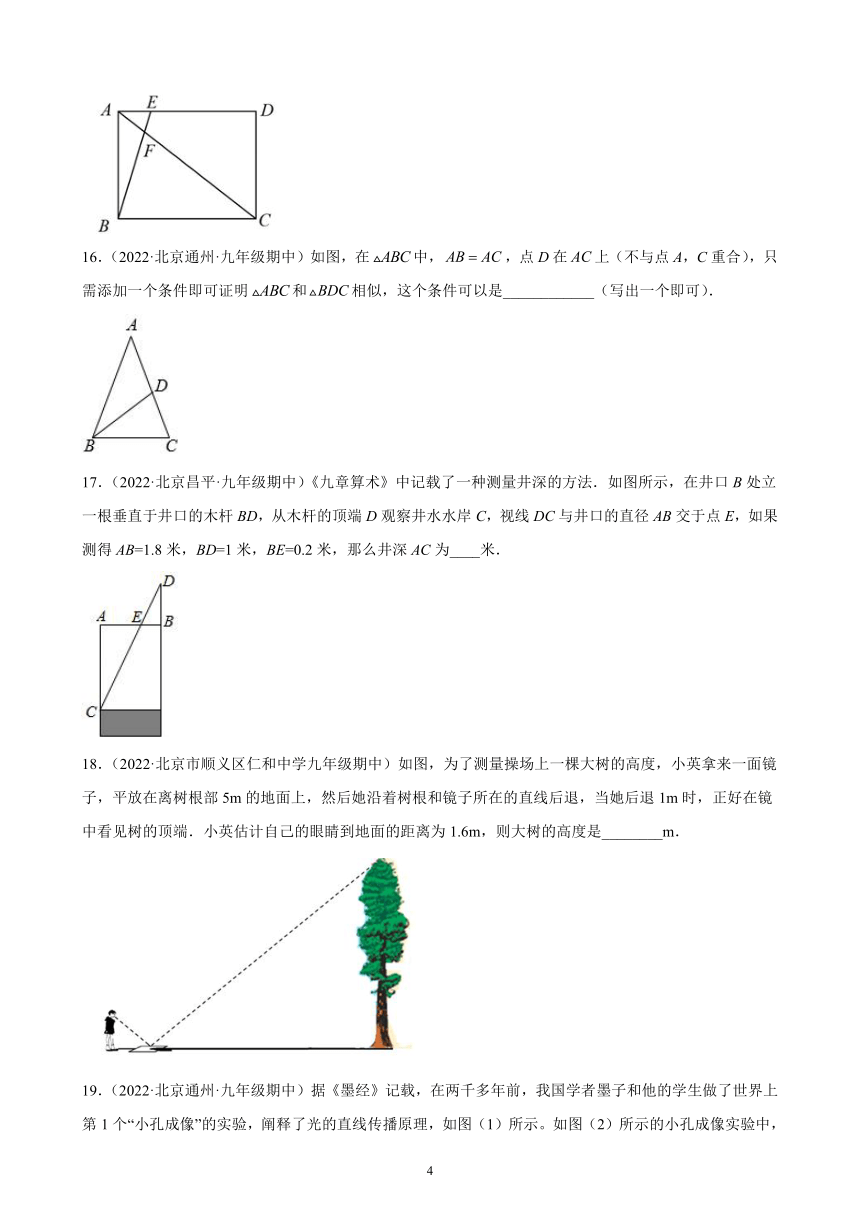
16.(2022·北京通州·九年级期中)如图,在中,,点D在上(不与点A,C重合),只需添加一个条件即可证明和相似,这个条件可以是____________(写出一个即可).
17.(2022·北京昌平·九年级期中)《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.8米,BD=1米,BE=0.2米,那么井深AC为____米.
18.(2022·北京市顺义区仁和中学九年级期中)如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部5m的地面上,然后她沿着树根和镜子所在的直线后退,当她后退1m时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为1.6m,则大树的高度是________m.
19.(2022·北京通州·九年级期中)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是_________cm.
三、解答题
20.(2022·北京通州·九年级期中)已知:如图,线段AB.
求作:点C,D,使得点C,D在线段AB上,且AC=CD=DB.
作法:①作射线AM,在射线AM上顺次截取线段AE=EF=FG,连接BG;
②以点E为圆心,BG长为半径画弧,再以点B为圆心,EG长为半径画弧,两弧在AB上方交于点H;
③连接BH,连接EH交AB于点C,在线段CB上截取线段CD=AC.
所以点C,D就是所求作的点.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵EH=BG,BH=EG,
∴四边形EGBH是平行四边形.(______)(填推理的依据)
∴,即.
∴AC∶______=AE∶AG.
∵AE=EF=FG,
∴AE=______AG.
∴.
∴.
∴AC=CD=DB.
21.(2022·北京昌平·模拟预测)数学课上,李老师出示了这样一道题目:如图,正方形ABCD的边长为12,P为边BC延长线上的一点,E为DP的中点,DP的垂直平分线交边DC于M,交边AB的延长线于N.当CP=6时,EM与EN的比值是多少?经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.
(1)请按照小明的思路写出求解过程.
(2)小东又对此题作了进一步探究,得出了DP=MN的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
22.(2022·北京通州·九年级期中)如图,AC,BD相交于的点O,且∠ABO=∠C.求证:△AOB∽△DOC.
23.(2022·北京·中国人民大学附属中学朝阳学校一模)已知:中,,,用尺规求作一条过点B的直线,使得截出的一个三角形与相似并证明.(保留作图痕迹,不写作法)
24.(2022·北京·清华附中一模)如图,AB∥CD,AC与BD的交点为E,∠ABE=∠ACB.
(1)求证:△ABE∽△ACB;
(2)如果AB=6,AE=4,求AC,CD的长.
25.(2022·北京市顺义区仁和中学九年级期中)如图,在平行四边形中,连接,是边上一点,连接并延长,交的延长线于,且.
(1)求证:;
(2)如果,,求的值.
26.(2022·北京通州·九年级期中)如图,是小凯为估算鱼塘的宽AB设计的,在陆地上取点,使得在同一条直线上,在同一条直线上,测得.小凯测得的长为10米,求鱼塘的宽的长是多少米?
27.(2022·北京昌平·九年级期中)学习完相似形一章之后,数学兴趣小组利用相似三角形的有关知识测量校园内一棵树高,他们的方法如下:
如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部的地面上,然后她沿着树根和镜子所在的直线后退,当她后退时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为,则可测得大树的高度.
(1)请你根据上述方法求出树高;
(2)请你设计一个其他的测量方案,并简述方案.
参考答案:
1.B
【分析】根据两内项之积等于两外项之积对各选项分析判断即可得解.
【详解】解:A、由得,2x=3y,故本选项不符合题意;
B、由得,3x=2y,故本选项符合题意;
C、由得,2x=3y,故本选项不符合题意;
D、由得,xy=6,故本选项不符合题意.
故选:B.
【点睛】本题考查了比例的性质,主要利用了两内项之积等于两外项之积,熟记性质是解题的关键.
2.A
【分析】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.对选项一一分析,排除错误答案.
【详解】解:A、1×4=2×2,故选项符合题意;
B、1×4≠2×3,故选项不符合题意;
C、3×13≠5×9,故选项不符合题意;
D、1×3≠2×2,故选项不符合题意.
故选:A.
【点睛】此题考查了比例线段,根据成比例线段的概念,注意在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.
3.B
【分析】根据黄金分割的定义,知为较长线段,则,代入数据即可得出的值.
【详解】解:是线段的黄金分割点,且,为较长线段,
,
,
,
.
故选:B.
【点睛】本题考查了黄金分割,用到的知识点是把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.
4.A
【分析】根据平行线分线段成比例定理得到AC:CE=BD:DF=1:2,然后利用比例性质即可得出答案进行选择.
【详解】解:∵AB∥CD∥EF,
∴AC:CE=BD:DF,
∵,
∴AC:CE=BD:DF=1:2,即CE=2AC,
∴AC:AE=1:3=.
故选A.
【点睛】本题考查平行线分线段成比例即三条平行线截两条直线,所得的对应线段成比例.
5.D
【详解】∵DE∥BC,∴,即,∴AC=8.故选D.
6.D
【分析】分别根据平行四边形、矩形、菱形及正方形的性质进行逐一判断即可.
【详解】解:A.因为两个平行四边形的对应角及对应边均不能确定,故任意两个平行四边形不一定相似,故本选项错误;
B.任意两个矩形的对应边不能确定,故任意两个矩形不一定相似,故本选项错误;
C.两个菱形的对应角不一定相等,故任意两个菱形不一定相似,故本选项错误;
D.由于正方形的四条边均相等,四个角都是直角,所以任意两个正方形一定相似,故本选项正确.
故选D.
【点睛】本题考查的是相似多边形的判定,熟知平行四边形、矩形、菱形及正方形的性质是解答此题的关键.
7.A
【分析】根据相似多边形的面积比等于相似比的平方,从而得解.
【详解】解:∵两个相似多边形的的相似比为,
∴它们面积之比为,
故选:A.
【点睛】本题考查了相似多边形的性质,熟知相似多边形的面积比等于相似比的平方是解本题的关键.
8.D
【分析】根据相似三角形的判定逐项判断即可.
【详解】A.∵,,∴,故原说法正确,不符合题意;
B. ∵,,∴,故原说法正确,不符合题意;
C.∵, ,∴,故原说法正确,不符合题意;
D. ∵,而不一定等于 ,∴与不一定相似,故原说法错误,符合题意.
故选:D.
【点睛】本题考查了相似三角形的判定,掌握相似三角形的判定方法,并能熟练运用是解题的关键.
9.C
【分析】利用相似三角形的判定方法依次判断可求解.
【详解】解:A、若,且,则,故选项A不合题意;
B、若,且,则,故选项B不合题意;
C、若,且,不能证明与相似,故选项C符合题意;
D、若,则,且,则,故选项D不合题意;
故选:C.
【点睛】本题考查了相似三角形的判定和性质,灵活运用所学知识求解是解决本题的关键.
10.A
【分析】根据两边成比例夹角相等两三角形相似即可判断.
【详解】解:由题意:①②④中,∠ABC=∠ADE=∠AFH=135°,
又∵,
∴,,
∴△ABC∽△ADE∽△HFA,
故选:A.
【点睛】本题考查相似三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
11.A
【详解】解:∵四边形ABCD是菱形,∠A=60°,∴∠ABD=∠CBD=∠ADB=∠BDC=60°,∴∠BDQ=∠BDP=120°,∵∠QBP=60°,∴∠OBD=∠PBC,∵AP∥BC,∴∠P=∠PBC,∴∠QBD=∠P,∴△BDQ∽△PDB,∴,即,∴xy=4,∴y与x的函数关系的图象是双曲线,故选A.
点睛:本题考查了菱形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.
12.A
【分析】根据平行线的判定定理确定,再根据相似三角形的判定定理和性质求解即可.
【详解】解:∵直线BD,CE均与直线AC垂直,
∴.
∴.
∴.
∵AB的长为x,
∴AC=AB+BC=x+BC.
∴.
故选:A.
【点睛】本题考查平行线的判定定理,相似三角形的判定定理和性质,熟练掌握这些知识点是解题关键.
13.
【分析】设x=3k,y=5k,其中(k≠0),代入即可消去k即可求解.
【详解】解:由可知,设x=3k,y=5k,其中(k≠0),
则x+y=8k,
∴,
故答案为:.
【点睛】本题考查了比例的基本性质及运算,属于基础题.
14.
【分析】根据黄金比值为计算即可.
【详解】解∶ 是线段的黄金分割点,且,,
∴,
∴.
故答案为:.
【点睛】本题考查的是黄金分割的概念,熟记黄金比值为是解题的关键.
15.1
【分析】根据勾股定理求出BC,以及平行线分线段成比例进行解答即可.
【详解】解:在矩形中, ,,
∴,,
∴,
∴,
故答案为:1.
【点睛】此题考查了勾股定理以及平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
16.∠A=∠CBD或∠ABC=∠BDC或或BC2=AC·DC(答案不唯一)
【分析】相似三角形的判定定理:①两边对应成比例且夹角相等的两个三角形相似;②两角对应相等的两个三角形相似.据此解答即可.
【详解】解:∵∠C=∠C
∴添加∠A=∠CBD或∠ABC=∠BDC或或BC2=AC·DC.
故答案为:∠A=∠CBD或∠ABC=∠BDC或或BC2=AC·DC(答案不唯一).
【点睛】此题考查了补充条件使两个三角形相似.解题的关键是熟知相似三角形的判定定理,特别注意用对应边成比例和一个角相等判定三角形相似的时候,其中相等的角一定要是这两条边的夹角.
17.8米.
【分析】根据相似三角形的判定和性质定理即可得到结论.
【详解】解:∵BD⊥AB,AC⊥AB,
∴BDAC,
∴△ACE∽△DBE,
∴,
∴,
∴AC=8(米),
故答案为:8(米) .
【点睛】本题考查了相似三角形的应用,正确的识别图形,掌握相似三角形的判定及性质是解决此类题的关键.
18.8
【分析】入射角等于反射角,两个直角相等,那么图中的两个三角形相似,利用对应边成比例可求得树高.
【详解】如图:
∵∠ABC=∠DBE,∠ACB=∠DEB=90°,
∴△ABC∽△DBE,
∴BC:BE=AC:DE,
即1:5=1.6:DE,
∴DE=8m,
故答案为:8.
【点睛】本题考查了相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
19.4
【分析】直接利用相似三角形的对应边成比例解答.
【详解】解:设蜡烛火焰的高度是xcm,
由相似三角形的性质得到:.
解得x=4.
即蜡烛火焰的高度是4cm.
故答案为:4.
【点睛】本题考查相似三角形的判定与性质的实际应用,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
20.(1)见解析;
(2)两组对边分别相等的四边形是平行四边形;AB;.
【分析】(1)根据要求作出图形即可.
(2)先证明四边形EGBH是平行四边形,再通过平行线分线段成比例定理来解决问题.
【详解】(1)、
补全图形如下图所示:
(2)证明:∵EH=BG,BH=EG,
∴四边形EGBH是平行四边形.(两组对边分别相等的四边形是平行四边形)
∴,即.
∴AC∶AB=AE∶AG.
∵AE=EF=FG,
∴AE=AG.
∴.
∴.
∴AC=CD=DB.
故答案为:两组对边分别相等的四边形是平行四边形;AB;.
【点睛】本题考查基本作图,平行四边形的判定和性质及平行线分线段成比例定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.(1)见解析
(2)正确,见解析
【分析】(1)过E作EG∥BC交DC、AB分别于F、G,结合平行线分线段成比例定理可得:,由DE=EP,可知DF=FC,可求出EF和EG的值,再利用AB∥CD,可得,进而可求得EM与EN的比值;
(2)作MH∥BC交AB于点H,可得一对直角和一组对应边相等,然后根据AB∥CD,可得∠MNH=∠CMN,结合对顶角的性质可证得∠DPC=∠MNH,进而可得△DPC≌△MNH,从而有DP=MN.
(1)
解:过E作直线GE平行于BC交DC,AB分别于点F,G,(如图1),
则,GF=BC=12,
∵DE=EP,
∴DF=FC,
∴EF=CP==3,EG=GF+EF=12+3=15,
∵AB∥CD,
∴;
(2)
解:正确,
证明:作MH∥BC交AB于点H,(如图2),
则MH=CB=CD,∠MHN=90°,
∵∠DCP=180°﹣90°=90°,
∴∠DCP=∠MHN,
∵AB∥CD,
∴∠MNH=∠CMN,
∵NE是DP的垂直平分线,
∴∠CMN=∠DME=90°﹣∠CDP,
∵∠DPC=90°﹣∠CDP,
∴∠DPC=∠MNH,
∴△DPC≌△MNH(AAS),
∴DP=MN.
【点睛】本题考查了正方形的性质,平行线分线段成比例定理、平行线的性质、全等三角形的判定和性质等知识.关键是作出合适的辅助线,使所求的线段在一个三角形中.
22.见解析
【分析】利用对顶角相等得到∠AOB=∠COD,再结合已知条件及相似三角形的判定定理即可求解.
【详解】证明:∵AC,BD相交于的点O,
∴∠AOB=∠DOC,
又∵∠ABO=∠C,
∴△AOB∽△DOC.
【点睛】本题考查了相似三角形的判定定理:若一对三角形的两组对应角相等,则这两个三角形相似,由此即可求解.
23.见详解
【分析】作∠ABC的角平分线,交AC于点D,再根据两角对应相等即可.
【详解】解:如图,直线BD即为所求.
证明:∵,,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,
∴∠BCD=36°,
∴∠BCD=∠A,
∵∠C=∠A,
∴
【点睛】本题主要考查了角平分线的作法,以及三角形相似的判定,解题的关键是三角形相似的判定.
24.(1)详见解析;(2)AC=9,CD=.
【分析】(1)根据相似三角形的判定证明即可;
(2)利用相似三角形的性质解答即可.
【详解】证明:(1)∵∠ABE=∠ACB,∠A=∠A,
∴△ABE∽△ACB;
(2)∵△ABE∽△ACB,
∴,
∴AB2=AC AE,
∵AB=6,AE=4,
∴AC=,
∵AB∥CD,
∴△CDE∽△ABE,
∴,
∴ .
【点睛】此题考查相似三角形的判定和性质,关键是根据相似三角形的判定证明△ABE∽△ACB.
25.(1)证明见解析
(2)
【分析】(1)根据平行四边形对角相等可得,又,等量代换可得,再结合公共角,即可证明;
(2)根据(1)的结论,列出比例式代入数值计算可得.
【详解】(1)证明:四边形是平行四边形,
,
,
,
又,
;
(2)解:,
,
,,
.
【点睛】本题考查了平行四边形的性质,相似三角形的性质与判定,掌握相似三角形的性质与判定是解题的关键.
26.20米
【分析】首先根据两边对应成比例且夹角相等可得,再根据对应边成比例可得答案.
【详解】解:∵
∴,
∵,
∴,
∴,
∵,
∴.
∴鱼塘的宽的长是20米.
【点睛】本题考查的是相似三角形的判定与性质,掌握“两边对应成比例且夹角相等的两个三角形相似”是解本题的关键.
27.(1)
(2)见解析
【分析】(1)入射角等于反射角,两个直角相等,那么图中的两个三角形相似,利用对应边成比例可求得树高;
(2)在距离树的米的处,用测角仪测得仰角,测角仪为再根据仰角的定义,构造直角三角形,利用三角函数计算可得答案.
【详解】(1)解:作图如下:
,,
∽,
,
即,
,
大树的高度为;
(2)解:在距离树的米的处,用测角仪测得仰角,测角仪为.
再根据仰角的定义,构造直角三角形,求得树高出测角仪的高度,则树高为.
【点睛】本题考查相似三角形性质的应用.解题的关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
一、单选题
1.(2022·北京房山·九年级期中)若,则下列比例式成立的是( )
A. B. C. D.
2.(2022·北京昌平·九年级期中)下列各组线段中,成比例的是( )
A.1,2,2,4 B.1,2,3,4
C.3,5,9,13 D.1,2,2,3
3.(2022·北京市顺义区仁和中学九年级期中)已知点是线段的黄金分割点,且,,则的长为( )
A. B. C. D.0.618
4.(2022·北京房山·九年级期中)如图,已知∥∥,,那么的值是( )
A. B. C. D.2
5.(2022·北京大兴·二模)如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD︰AB=3︰4,AE=6,则AC等于( )
A.3
B.4
C.6
D.8
6.(2022·北京通州·九年级期中)下列判断正确的是( )
A.任意两个平行四边形一定相似 B.任意两个矩形一定相似
C.任意两个菱形一定相似 D.任意两个正方形一定相似
7.(2022·北京市大峪中学分校九年级期中)若两个相似多边形的的相似比为,则它们面积之比为( )
A. B. C. D.
8.(2022·北京·大峪中学九年级期中)如图,是的边上一点,那么下面四个命题中错误的是( )
A.如果,那么
B.如果,那么
C.如果,那么
D.如果,那么
9.(2022·北京房山·九年级期中)如图,F是的边上一点,则下列条件不能判定与相似的是( )
A. B. C. D.
10.(2022·北京·九年级单元测试)如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
11.(2022·北京双榆树中学九年级期中)如图,菱形ABCD的边长为2,∠A=60°,一个以点B为顶点的60°角绕点B旋转,这个角的两边分别与线段AD的延长线及CD的延长线交于点P、Q,设DP=x,DQ=y,则能大致反映y与x的函数关系的图象是( )
A. B.
C. D.
12.(2022·北京海淀·二模)图,为了估算河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,E,使得A,B与C共线,A,D与E共线,且直线AC与河岸垂直,直线BD,CE均与直线AC垂直.经测量,得到BC,CE,BD的长度,设AB的长为x,则下列等式成立的是( )
A. B. C. D.
二、填空题
13.(2022·北京·人大附中通州校区九年级阶段练习)已知,那的值为___________.
14.(2022·北京市第九中学九年级期中)已知是线段的黄金分割点,且,若,则短线段的长度为______.
15.(2022·北京·九年级专题练习)如图,在矩形中,若,则的长为_______.
16.(2022·北京通州·九年级期中)如图,在中,,点D在上(不与点A,C重合),只需添加一个条件即可证明和相似,这个条件可以是____________(写出一个即可).
17.(2022·北京昌平·九年级期中)《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.8米,BD=1米,BE=0.2米,那么井深AC为____米.
18.(2022·北京市顺义区仁和中学九年级期中)如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部5m的地面上,然后她沿着树根和镜子所在的直线后退,当她后退1m时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为1.6m,则大树的高度是________m.
19.(2022·北京通州·九年级期中)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是_________cm.
三、解答题
20.(2022·北京通州·九年级期中)已知:如图,线段AB.
求作:点C,D,使得点C,D在线段AB上,且AC=CD=DB.
作法:①作射线AM,在射线AM上顺次截取线段AE=EF=FG,连接BG;
②以点E为圆心,BG长为半径画弧,再以点B为圆心,EG长为半径画弧,两弧在AB上方交于点H;
③连接BH,连接EH交AB于点C,在线段CB上截取线段CD=AC.
所以点C,D就是所求作的点.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵EH=BG,BH=EG,
∴四边形EGBH是平行四边形.(______)(填推理的依据)
∴,即.
∴AC∶______=AE∶AG.
∵AE=EF=FG,
∴AE=______AG.
∴.
∴.
∴AC=CD=DB.
21.(2022·北京昌平·模拟预测)数学课上,李老师出示了这样一道题目:如图,正方形ABCD的边长为12,P为边BC延长线上的一点,E为DP的中点,DP的垂直平分线交边DC于M,交边AB的延长线于N.当CP=6时,EM与EN的比值是多少?经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.
(1)请按照小明的思路写出求解过程.
(2)小东又对此题作了进一步探究,得出了DP=MN的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
22.(2022·北京通州·九年级期中)如图,AC,BD相交于的点O,且∠ABO=∠C.求证:△AOB∽△DOC.
23.(2022·北京·中国人民大学附属中学朝阳学校一模)已知:中,,,用尺规求作一条过点B的直线,使得截出的一个三角形与相似并证明.(保留作图痕迹,不写作法)
24.(2022·北京·清华附中一模)如图,AB∥CD,AC与BD的交点为E,∠ABE=∠ACB.
(1)求证:△ABE∽△ACB;
(2)如果AB=6,AE=4,求AC,CD的长.
25.(2022·北京市顺义区仁和中学九年级期中)如图,在平行四边形中,连接,是边上一点,连接并延长,交的延长线于,且.
(1)求证:;
(2)如果,,求的值.
26.(2022·北京通州·九年级期中)如图,是小凯为估算鱼塘的宽AB设计的,在陆地上取点,使得在同一条直线上,在同一条直线上,测得.小凯测得的长为10米,求鱼塘的宽的长是多少米?
27.(2022·北京昌平·九年级期中)学习完相似形一章之后,数学兴趣小组利用相似三角形的有关知识测量校园内一棵树高,他们的方法如下:
如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部的地面上,然后她沿着树根和镜子所在的直线后退,当她后退时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为,则可测得大树的高度.
(1)请你根据上述方法求出树高;
(2)请你设计一个其他的测量方案,并简述方案.
参考答案:
1.B
【分析】根据两内项之积等于两外项之积对各选项分析判断即可得解.
【详解】解:A、由得,2x=3y,故本选项不符合题意;
B、由得,3x=2y,故本选项符合题意;
C、由得,2x=3y,故本选项不符合题意;
D、由得,xy=6,故本选项不符合题意.
故选:B.
【点睛】本题考查了比例的性质,主要利用了两内项之积等于两外项之积,熟记性质是解题的关键.
2.A
【分析】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.对选项一一分析,排除错误答案.
【详解】解:A、1×4=2×2,故选项符合题意;
B、1×4≠2×3,故选项不符合题意;
C、3×13≠5×9,故选项不符合题意;
D、1×3≠2×2,故选项不符合题意.
故选:A.
【点睛】此题考查了比例线段,根据成比例线段的概念,注意在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.
3.B
【分析】根据黄金分割的定义,知为较长线段,则,代入数据即可得出的值.
【详解】解:是线段的黄金分割点,且,为较长线段,
,
,
,
.
故选:B.
【点睛】本题考查了黄金分割,用到的知识点是把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.
4.A
【分析】根据平行线分线段成比例定理得到AC:CE=BD:DF=1:2,然后利用比例性质即可得出答案进行选择.
【详解】解:∵AB∥CD∥EF,
∴AC:CE=BD:DF,
∵,
∴AC:CE=BD:DF=1:2,即CE=2AC,
∴AC:AE=1:3=.
故选A.
【点睛】本题考查平行线分线段成比例即三条平行线截两条直线,所得的对应线段成比例.
5.D
【详解】∵DE∥BC,∴,即,∴AC=8.故选D.
6.D
【分析】分别根据平行四边形、矩形、菱形及正方形的性质进行逐一判断即可.
【详解】解:A.因为两个平行四边形的对应角及对应边均不能确定,故任意两个平行四边形不一定相似,故本选项错误;
B.任意两个矩形的对应边不能确定,故任意两个矩形不一定相似,故本选项错误;
C.两个菱形的对应角不一定相等,故任意两个菱形不一定相似,故本选项错误;
D.由于正方形的四条边均相等,四个角都是直角,所以任意两个正方形一定相似,故本选项正确.
故选D.
【点睛】本题考查的是相似多边形的判定,熟知平行四边形、矩形、菱形及正方形的性质是解答此题的关键.
7.A
【分析】根据相似多边形的面积比等于相似比的平方,从而得解.
【详解】解:∵两个相似多边形的的相似比为,
∴它们面积之比为,
故选:A.
【点睛】本题考查了相似多边形的性质,熟知相似多边形的面积比等于相似比的平方是解本题的关键.
8.D
【分析】根据相似三角形的判定逐项判断即可.
【详解】A.∵,,∴,故原说法正确,不符合题意;
B. ∵,,∴,故原说法正确,不符合题意;
C.∵, ,∴,故原说法正确,不符合题意;
D. ∵,而不一定等于 ,∴与不一定相似,故原说法错误,符合题意.
故选:D.
【点睛】本题考查了相似三角形的判定,掌握相似三角形的判定方法,并能熟练运用是解题的关键.
9.C
【分析】利用相似三角形的判定方法依次判断可求解.
【详解】解:A、若,且,则,故选项A不合题意;
B、若,且,则,故选项B不合题意;
C、若,且,不能证明与相似,故选项C符合题意;
D、若,则,且,则,故选项D不合题意;
故选:C.
【点睛】本题考查了相似三角形的判定和性质,灵活运用所学知识求解是解决本题的关键.
10.A
【分析】根据两边成比例夹角相等两三角形相似即可判断.
【详解】解:由题意:①②④中,∠ABC=∠ADE=∠AFH=135°,
又∵,
∴,,
∴△ABC∽△ADE∽△HFA,
故选:A.
【点睛】本题考查相似三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
11.A
【详解】解:∵四边形ABCD是菱形,∠A=60°,∴∠ABD=∠CBD=∠ADB=∠BDC=60°,∴∠BDQ=∠BDP=120°,∵∠QBP=60°,∴∠OBD=∠PBC,∵AP∥BC,∴∠P=∠PBC,∴∠QBD=∠P,∴△BDQ∽△PDB,∴,即,∴xy=4,∴y与x的函数关系的图象是双曲线,故选A.
点睛:本题考查了菱形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.
12.A
【分析】根据平行线的判定定理确定,再根据相似三角形的判定定理和性质求解即可.
【详解】解:∵直线BD,CE均与直线AC垂直,
∴.
∴.
∴.
∵AB的长为x,
∴AC=AB+BC=x+BC.
∴.
故选:A.
【点睛】本题考查平行线的判定定理,相似三角形的判定定理和性质,熟练掌握这些知识点是解题关键.
13.
【分析】设x=3k,y=5k,其中(k≠0),代入即可消去k即可求解.
【详解】解:由可知,设x=3k,y=5k,其中(k≠0),
则x+y=8k,
∴,
故答案为:.
【点睛】本题考查了比例的基本性质及运算,属于基础题.
14.
【分析】根据黄金比值为计算即可.
【详解】解∶ 是线段的黄金分割点,且,,
∴,
∴.
故答案为:.
【点睛】本题考查的是黄金分割的概念,熟记黄金比值为是解题的关键.
15.1
【分析】根据勾股定理求出BC,以及平行线分线段成比例进行解答即可.
【详解】解:在矩形中, ,,
∴,,
∴,
∴,
故答案为:1.
【点睛】此题考查了勾股定理以及平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
16.∠A=∠CBD或∠ABC=∠BDC或或BC2=AC·DC(答案不唯一)
【分析】相似三角形的判定定理:①两边对应成比例且夹角相等的两个三角形相似;②两角对应相等的两个三角形相似.据此解答即可.
【详解】解:∵∠C=∠C
∴添加∠A=∠CBD或∠ABC=∠BDC或或BC2=AC·DC.
故答案为:∠A=∠CBD或∠ABC=∠BDC或或BC2=AC·DC(答案不唯一).
【点睛】此题考查了补充条件使两个三角形相似.解题的关键是熟知相似三角形的判定定理,特别注意用对应边成比例和一个角相等判定三角形相似的时候,其中相等的角一定要是这两条边的夹角.
17.8米.
【分析】根据相似三角形的判定和性质定理即可得到结论.
【详解】解:∵BD⊥AB,AC⊥AB,
∴BDAC,
∴△ACE∽△DBE,
∴,
∴,
∴AC=8(米),
故答案为:8(米) .
【点睛】本题考查了相似三角形的应用,正确的识别图形,掌握相似三角形的判定及性质是解决此类题的关键.
18.8
【分析】入射角等于反射角,两个直角相等,那么图中的两个三角形相似,利用对应边成比例可求得树高.
【详解】如图:
∵∠ABC=∠DBE,∠ACB=∠DEB=90°,
∴△ABC∽△DBE,
∴BC:BE=AC:DE,
即1:5=1.6:DE,
∴DE=8m,
故答案为:8.
【点睛】本题考查了相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
19.4
【分析】直接利用相似三角形的对应边成比例解答.
【详解】解:设蜡烛火焰的高度是xcm,
由相似三角形的性质得到:.
解得x=4.
即蜡烛火焰的高度是4cm.
故答案为:4.
【点睛】本题考查相似三角形的判定与性质的实际应用,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
20.(1)见解析;
(2)两组对边分别相等的四边形是平行四边形;AB;.
【分析】(1)根据要求作出图形即可.
(2)先证明四边形EGBH是平行四边形,再通过平行线分线段成比例定理来解决问题.
【详解】(1)、
补全图形如下图所示:
(2)证明:∵EH=BG,BH=EG,
∴四边形EGBH是平行四边形.(两组对边分别相等的四边形是平行四边形)
∴,即.
∴AC∶AB=AE∶AG.
∵AE=EF=FG,
∴AE=AG.
∴.
∴.
∴AC=CD=DB.
故答案为:两组对边分别相等的四边形是平行四边形;AB;.
【点睛】本题考查基本作图,平行四边形的判定和性质及平行线分线段成比例定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.(1)见解析
(2)正确,见解析
【分析】(1)过E作EG∥BC交DC、AB分别于F、G,结合平行线分线段成比例定理可得:,由DE=EP,可知DF=FC,可求出EF和EG的值,再利用AB∥CD,可得,进而可求得EM与EN的比值;
(2)作MH∥BC交AB于点H,可得一对直角和一组对应边相等,然后根据AB∥CD,可得∠MNH=∠CMN,结合对顶角的性质可证得∠DPC=∠MNH,进而可得△DPC≌△MNH,从而有DP=MN.
(1)
解:过E作直线GE平行于BC交DC,AB分别于点F,G,(如图1),
则,GF=BC=12,
∵DE=EP,
∴DF=FC,
∴EF=CP==3,EG=GF+EF=12+3=15,
∵AB∥CD,
∴;
(2)
解:正确,
证明:作MH∥BC交AB于点H,(如图2),
则MH=CB=CD,∠MHN=90°,
∵∠DCP=180°﹣90°=90°,
∴∠DCP=∠MHN,
∵AB∥CD,
∴∠MNH=∠CMN,
∵NE是DP的垂直平分线,
∴∠CMN=∠DME=90°﹣∠CDP,
∵∠DPC=90°﹣∠CDP,
∴∠DPC=∠MNH,
∴△DPC≌△MNH(AAS),
∴DP=MN.
【点睛】本题考查了正方形的性质,平行线分线段成比例定理、平行线的性质、全等三角形的判定和性质等知识.关键是作出合适的辅助线,使所求的线段在一个三角形中.
22.见解析
【分析】利用对顶角相等得到∠AOB=∠COD,再结合已知条件及相似三角形的判定定理即可求解.
【详解】证明:∵AC,BD相交于的点O,
∴∠AOB=∠DOC,
又∵∠ABO=∠C,
∴△AOB∽△DOC.
【点睛】本题考查了相似三角形的判定定理:若一对三角形的两组对应角相等,则这两个三角形相似,由此即可求解.
23.见详解
【分析】作∠ABC的角平分线,交AC于点D,再根据两角对应相等即可.
【详解】解:如图,直线BD即为所求.
证明:∵,,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,
∴∠BCD=36°,
∴∠BCD=∠A,
∵∠C=∠A,
∴
【点睛】本题主要考查了角平分线的作法,以及三角形相似的判定,解题的关键是三角形相似的判定.
24.(1)详见解析;(2)AC=9,CD=.
【分析】(1)根据相似三角形的判定证明即可;
(2)利用相似三角形的性质解答即可.
【详解】证明:(1)∵∠ABE=∠ACB,∠A=∠A,
∴△ABE∽△ACB;
(2)∵△ABE∽△ACB,
∴,
∴AB2=AC AE,
∵AB=6,AE=4,
∴AC=,
∵AB∥CD,
∴△CDE∽△ABE,
∴,
∴ .
【点睛】此题考查相似三角形的判定和性质,关键是根据相似三角形的判定证明△ABE∽△ACB.
25.(1)证明见解析
(2)
【分析】(1)根据平行四边形对角相等可得,又,等量代换可得,再结合公共角,即可证明;
(2)根据(1)的结论,列出比例式代入数值计算可得.
【详解】(1)证明:四边形是平行四边形,
,
,
,
又,
;
(2)解:,
,
,,
.
【点睛】本题考查了平行四边形的性质,相似三角形的性质与判定,掌握相似三角形的性质与判定是解题的关键.
26.20米
【分析】首先根据两边对应成比例且夹角相等可得,再根据对应边成比例可得答案.
【详解】解:∵
∴,
∵,
∴,
∴,
∵,
∴.
∴鱼塘的宽的长是20米.
【点睛】本题考查的是相似三角形的判定与性质,掌握“两边对应成比例且夹角相等的两个三角形相似”是解本题的关键.
27.(1)
(2)见解析
【分析】(1)入射角等于反射角,两个直角相等,那么图中的两个三角形相似,利用对应边成比例可求得树高;
(2)在距离树的米的处,用测角仪测得仰角,测角仪为再根据仰角的定义,构造直角三角形,利用三角函数计算可得答案.
【详解】(1)解:作图如下:
,,
∽,
,
即,
,
大树的高度为;
(2)解:在距离树的米的处,用测角仪测得仰角,测角仪为.
再根据仰角的定义,构造直角三角形,求得树高出测角仪的高度,则树高为.
【点睛】本题考查相似三角形性质的应用.解题的关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
