【精选备课】2022-2023学年华师大版数学八年级上册 11.1.1 平方根 课件(42张PPT)
文档属性
| 名称 | 【精选备课】2022-2023学年华师大版数学八年级上册 11.1.1 平方根 课件(42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 264.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 19:58:41 | ||
图片预览










文档简介
11.1.1 平方根
教学目标
1、了解一个数的平方根与算术平方根的意义,会用根号表示一个数的平方根、算术平方根. 2、了解开方与乘方是互逆运算,会利用这个逆运算关系求某些非负数的算术平方根.
教学重难点
教学重点: 了解一个数的平方根与算术平方根的意义,会用根号表示一个数的平方根、算术平方根. 教学难点: 了解开方与乘方是互逆运算,会利用这个逆运算关系求某些非负数的算术平方根.
回顾思考
同学们,我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中: 加法与减法互为逆运算;乘法与除法互为逆运算;那么乘方与谁互为逆运算呢? 本节课我们就来学习研究这个问题。
底数
幂
指数
1.要做一张边长是3分米的正方形画布,它的面积是多少?
这个问题实际上就是求:
3分米
答:9平方分米。
这是已知底数和指数,求幂的运算。即我们学习过的乘方运算。
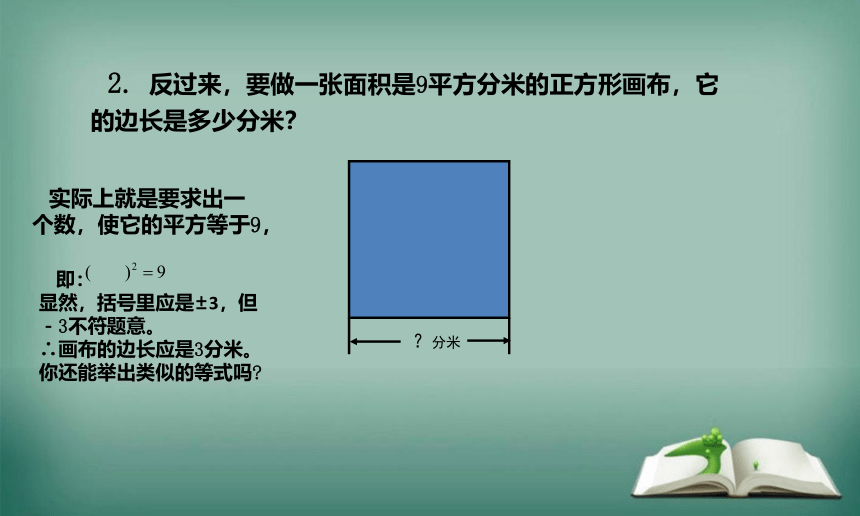
2. 反过来,要做一张面积是9平方分米的正方形画布,它的边长是多少分米?
?分米
实际上就是要求出一个数,使它的平方等于9,
即: 显然,括号里应是±3,但-3不符题意。 ∴画布的边长应是3分米。 你还能举出类似的等式吗?
3.认真观察下式可知:
±3
我们把括号里的±3叫做9的平方根(二次方根)。
一般地,如果 ,那么 叫 的平方根。
开方和乘方是互为逆运算
例如:
(1)
(2)
∵
∴5 和 -5 都是25的平方根。
25的平方根是±5
以小组合作的形式完成下列问题,并派代表进行反馈,其他同学注意听并做相应的评价、补充、纠错
(1)144的平方根是什么? (2)0的平方根是什么? (3)-4的平方根是什么? 为什么? 从上面的回答中,你发现了什么?
探索:
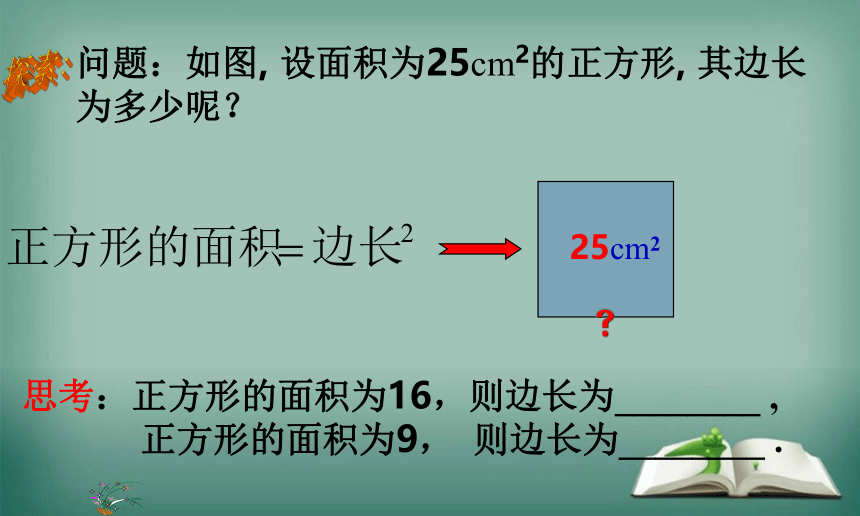
问题:如图, 设面积为25cm2的正方形, 其边长
为多少呢?
25cm2
思考:正方形的面积为16,则边长为________ ,
正方形的面积为9, 则边长为________ .
5
a
问题:如图, 设面积为5的正方形, 其边长为多少呢?若正方形的面积为a, 则边长又是多少呢?
概念:如果一个数x的平方等于a,那么这个数
x叫做a的平方根.
温馨提示
在a是非负数的前提下,a是x的平方,反之,x是a的平方根
a是x的平方 ,
x是a的平方根。
X2
底数
指数
幂
=
a
学以致用
下列说法中不正确的是( )
A.-3是9的平方根
B.3是9的平方根
C.9的平方根是3
D.9的平方根是±3
学以致用
下列说法中不正确的是( C )
A.-3是9的平方根
B.3是9的平方根
C.9的平方根是3
D.9的平方根是±3
例1、求100的平方根:
解 :
因为102=100,(-10)2=100,即(±10)2=100
所以100的平方根是±10,即
巩固训练:
求下列各数的平方根:
(1)121; (2)
(3) (4)0
巩固训练答案:
求下列各数的平方根:
(1) (2)
(3) (4)0
尝试完成“试一试”中的三个问题。
(1)144的平方根是什么?
(2)0的平方根是什么?
(3 )—4 有没有平方根?为什么?
思考:通过这些题目的解答,你能发现什么?你能试着总结一下平方根的性质吗?
探究二:平方根的性质
概括
平方根的性质:
(1)一个正数有两个平方根,它们互为相反数。
(2)0的平方根是0
(3)负数没有平方根。
思考:a有没有平方根?为什么?
思考:a有没有平方根?为什么?
当a≥0时, a有平方根,当a<0时,没有平方根。
巩固训练
1.判断下列说法是否正确:
(1)-9的平方根是-3; ( )
(2)49的平方根是7 ; ( )
(3)(-2)2的平方根是±2 ; ( )
(4)1 的平方根是 1 ; ( )
(5)-1 是 1的平方根; ( )
(6)7的平方根是±49. ( )
(7)若X2 = 16 , 则X = 4 ( )
巩固训练
1.判断下列说法是否正确:
(1)-9的平方根是-3; (× )
(2)49的平方根是7 ; (× )
(3)(-2)2的平方根是±2 ; ( √ )
(4)1 的平方根是 1 ; ( ×)
(5)-1 是 1的平方根; (√ )
(6)7的平方根是±49. (× )
(7)若X2 = 16 , 则X = 4 (× )
2、下列说法正确的是( )
A任何数都有平方根 B任何数的平方根都有两个
C 4是16的一个平方根 D(-5)2没有平方根
3、下列说法①±5是25的平方根。②49的平方根是-7. ③-36没有平方根。④一个数的平方根不一定有两个。其中正确的个数是( )
A 1 B 2 C 3 D 4
2、下列说法正确的是( C )
A任何数都有平方根 B任何数的平方根都有两个
C 4是16的一个平方根。D(-5)2没有平方根
3、下列说法①±5是25的平方根。②49的平方根是-7. ③-36没有平方根。④一个数的平方根不一定有两个。其中正确的个数是(C )
A 1 B 2 C 3 D 4
拓展提升
6、已知一个正数的平方根分别是 2a+1和 5-a , 求这个数。
解 :由题意知: 2a+1+ 5-a=0
解得a=-6,
所以2a+1=-11,5-a =11,
因为
所以这个数是121.
达标检测
1.一个数的平方等于5,这个数是 。
3.求下列各数的平方根;
(1)0.04; (2) (3)
4.已知2a-1的一个平方根是3,求2a-1的另一个平方根及a的值。
巩固训练
利用平方根的定义性质解方程
1)x2=4 2)x2=
3) 2x2=8 4)x2-49=0
例2利用平方根的定义性质解方程
1)x2=64 2)x2=
3)2x2=32 4)x2-25=0
作业
课本4页练习题第2、4题
课堂小结
1、如果一个数的平方等于 a,那么这个数叫做 a 的平方根(或者二次方根).
2、平方根的性质:
(1)一个正数有两个平方根,它们互为相反数。
(2)0的平方根是0
(3)负数没有平方根。
教学目标
1、了解一个数的平方根与算术平方根的意义,会用根号表示一个数的平方根、算术平方根. 2、了解开方与乘方是互逆运算,会利用这个逆运算关系求某些非负数的算术平方根.
教学重难点
教学重点: 了解一个数的平方根与算术平方根的意义,会用根号表示一个数的平方根、算术平方根. 教学难点: 了解开方与乘方是互逆运算,会利用这个逆运算关系求某些非负数的算术平方根.
回顾思考
同学们,我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中: 加法与减法互为逆运算;乘法与除法互为逆运算;那么乘方与谁互为逆运算呢? 本节课我们就来学习研究这个问题。
底数
幂
指数
1.要做一张边长是3分米的正方形画布,它的面积是多少?
这个问题实际上就是求:
3分米
答:9平方分米。
这是已知底数和指数,求幂的运算。即我们学习过的乘方运算。
2. 反过来,要做一张面积是9平方分米的正方形画布,它的边长是多少分米?
?分米
实际上就是要求出一个数,使它的平方等于9,
即: 显然,括号里应是±3,但-3不符题意。 ∴画布的边长应是3分米。 你还能举出类似的等式吗?
3.认真观察下式可知:
±3
我们把括号里的±3叫做9的平方根(二次方根)。
一般地,如果 ,那么 叫 的平方根。
开方和乘方是互为逆运算
例如:
(1)
(2)
∵
∴5 和 -5 都是25的平方根。
25的平方根是±5
以小组合作的形式完成下列问题,并派代表进行反馈,其他同学注意听并做相应的评价、补充、纠错
(1)144的平方根是什么? (2)0的平方根是什么? (3)-4的平方根是什么? 为什么? 从上面的回答中,你发现了什么?
探索:
问题:如图, 设面积为25cm2的正方形, 其边长
为多少呢?
25cm2
思考:正方形的面积为16,则边长为________ ,
正方形的面积为9, 则边长为________ .
5
a
问题:如图, 设面积为5的正方形, 其边长为多少呢?若正方形的面积为a, 则边长又是多少呢?
概念:如果一个数x的平方等于a,那么这个数
x叫做a的平方根.
温馨提示
在a是非负数的前提下,a是x的平方,反之,x是a的平方根
a是x的平方 ,
x是a的平方根。
X2
底数
指数
幂
=
a
学以致用
下列说法中不正确的是( )
A.-3是9的平方根
B.3是9的平方根
C.9的平方根是3
D.9的平方根是±3
学以致用
下列说法中不正确的是( C )
A.-3是9的平方根
B.3是9的平方根
C.9的平方根是3
D.9的平方根是±3
例1、求100的平方根:
解 :
因为102=100,(-10)2=100,即(±10)2=100
所以100的平方根是±10,即
巩固训练:
求下列各数的平方根:
(1)121; (2)
(3) (4)0
巩固训练答案:
求下列各数的平方根:
(1) (2)
(3) (4)0
尝试完成“试一试”中的三个问题。
(1)144的平方根是什么?
(2)0的平方根是什么?
(3 )—4 有没有平方根?为什么?
思考:通过这些题目的解答,你能发现什么?你能试着总结一下平方根的性质吗?
探究二:平方根的性质
概括
平方根的性质:
(1)一个正数有两个平方根,它们互为相反数。
(2)0的平方根是0
(3)负数没有平方根。
思考:a有没有平方根?为什么?
思考:a有没有平方根?为什么?
当a≥0时, a有平方根,当a<0时,没有平方根。
巩固训练
1.判断下列说法是否正确:
(1)-9的平方根是-3; ( )
(2)49的平方根是7 ; ( )
(3)(-2)2的平方根是±2 ; ( )
(4)1 的平方根是 1 ; ( )
(5)-1 是 1的平方根; ( )
(6)7的平方根是±49. ( )
(7)若X2 = 16 , 则X = 4 ( )
巩固训练
1.判断下列说法是否正确:
(1)-9的平方根是-3; (× )
(2)49的平方根是7 ; (× )
(3)(-2)2的平方根是±2 ; ( √ )
(4)1 的平方根是 1 ; ( ×)
(5)-1 是 1的平方根; (√ )
(6)7的平方根是±49. (× )
(7)若X2 = 16 , 则X = 4 (× )
2、下列说法正确的是( )
A任何数都有平方根 B任何数的平方根都有两个
C 4是16的一个平方根 D(-5)2没有平方根
3、下列说法①±5是25的平方根。②49的平方根是-7. ③-36没有平方根。④一个数的平方根不一定有两个。其中正确的个数是( )
A 1 B 2 C 3 D 4
2、下列说法正确的是( C )
A任何数都有平方根 B任何数的平方根都有两个
C 4是16的一个平方根。D(-5)2没有平方根
3、下列说法①±5是25的平方根。②49的平方根是-7. ③-36没有平方根。④一个数的平方根不一定有两个。其中正确的个数是(C )
A 1 B 2 C 3 D 4
拓展提升
6、已知一个正数的平方根分别是 2a+1和 5-a , 求这个数。
解 :由题意知: 2a+1+ 5-a=0
解得a=-6,
所以2a+1=-11,5-a =11,
因为
所以这个数是121.
达标检测
1.一个数的平方等于5,这个数是 。
3.求下列各数的平方根;
(1)0.04; (2) (3)
4.已知2a-1的一个平方根是3,求2a-1的另一个平方根及a的值。
巩固训练
利用平方根的定义性质解方程
1)x2=4 2)x2=
3) 2x2=8 4)x2-49=0
例2利用平方根的定义性质解方程
1)x2=64 2)x2=
3)2x2=32 4)x2-25=0
作业
课本4页练习题第2、4题
课堂小结
1、如果一个数的平方等于 a,那么这个数叫做 a 的平方根(或者二次方根).
2、平方根的性质:
(1)一个正数有两个平方根,它们互为相反数。
(2)0的平方根是0
(3)负数没有平方根。
