华师大版八年级上册 12.3.1 两数和乘以这两数的差 课件(共16张PPT)
文档属性
| 名称 | 华师大版八年级上册 12.3.1 两数和乘以这两数的差 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 651.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 21:33:31 | ||
图片预览






文档简介
(共16张PPT)
12.3.1两数和乘以这两数的差
教学目标
(1)理解和掌握平方差公式的特点;
(2)利用平方差公式进行多项式乘法的运算;
(3)通过小组合作、讨论,培养学生实际动手操作能力和与人交流、分享的人际关系;
(4)感受数形结合思想和建模思想解决数学问题的重要性;
(5)感知公式体现的数学美;
(6)体会从前后一致,逻辑连贯的数学演化思维以及从一般到特殊,再从特殊回归一般的事物本质;
张威同学去商店买单价是9.8元/千克的糖块10.2千克,售货员刚拿起计算器,张威就说出应付99.96元,结果与售货员计算出的结果相吻合。售货员惊讶地问:“这位同学,你怎么算得这么快 ”张威同学说:“我用了在数学课上刚学过的一个公式。”你知道张威同学用的是一个什么样的公式吗 学了本节后,你就能解决这个问题了。
情景导入
3.计算:
(1)(x+3)(x-3); (2)(a+2b)(a-2b);
(3)(4m+n)(4m-n); (4)(5+4y)(5-4y)。
1.多项式乘以多项式的法则:_______。
2.利用多项式与多项式的乘法法则说出
(x+a)(x+b)的结果。
(x+a)(x+b)=x2+(a+b)x+ab
温故知新
相互检查,交流心得
(x+3)(x-3)
(a+2b)(a-2b)
(4m+n)(4m-n)
(5+4y)(5-4y)
观察两个多项式的特征,再看看结果和这两个多项式各项的关系:
x2-9
a2-4b2
16m2-n2
25-16y2
a2-b2
(a+b)(a-b)
探索新知
(a+b)(a-b) a b a2-b2 结果
(y+3)(y-3)
(2m-n)(2m+n)
(-x+2)(-x-2)
(1-5b)(5b+1)
(-2x-3y)(-3y+2x)
找一找:
y2-32
y
3
y2-9
2m
n
(2m)2-n2
4m2-n2
-x
2
(-x)2-22
x2-4
1
5b
12-(5b)2
1-25b2
-3y
2x
(-3y)2-(2x)2
可以用多项式的乘法法则验证结果的正确性哟!
9y2-4x2
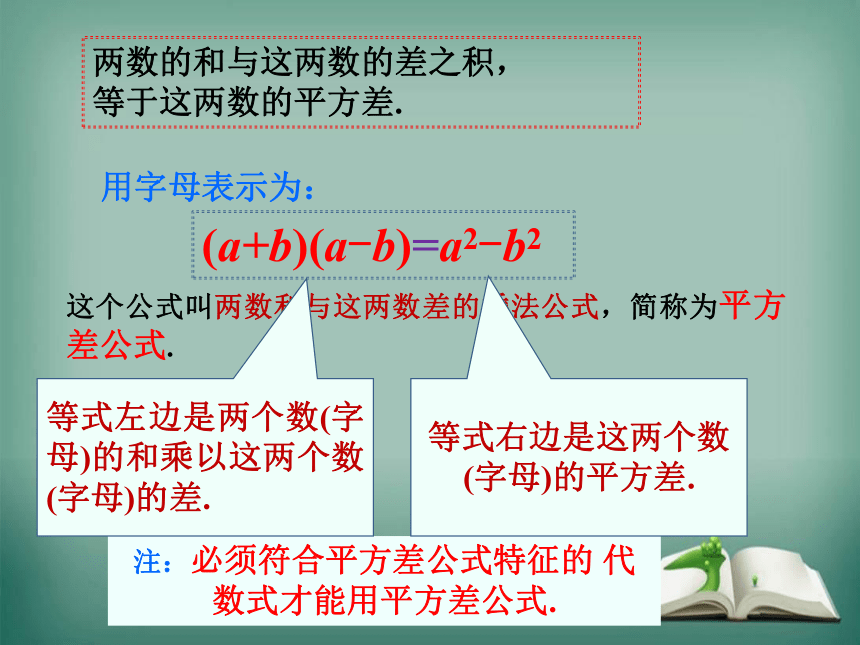
用字母表示为:
这个公式叫两数和与这两数差的乘法公式,简称为平方差公式.
注:必须符合平方差公式特征的 代数式才能用平方差公式.
两数的和与这两数的差之积,
等于这两数的平方差.
(a+b)(a-b)=a2-b2
等式左边是两个数(字母)的和乘以这两个数(字母)的差.
等式右边是这两个数(字母)的平方差.
你能说出平方差公式的几何意义吗?(即用图形面积来解释这个公式)
a
a
b
(a+b)(a-b)
a
a-b
b
a2
-b2
=
用图形面积解释公式,
这就是数形结合的思想.
表示长为(a+b)、宽为(a-b)的矩形面积等于边长为a、b的两正方形面积之差.
a2
b2
1、计算:
(1)(a+5)(5-a);
(2)(2a2-3b)(2a2+3b);
解:(1)原式=52-a2
=25-a2
(2)原式=(2a2)2-(3b)2
=4a4-9b2
(3)a(a-5)-(a+6)(a-6); (4)(x-y)(x+y)(x2+y2).
解: a(a-5)-(a+6)(a-6)
= a2-5a-(a2-62)
= a2-5a-a2+36
= -5a+36
解: (x-y)(x+y)(x2+y2)
= (x2-y2)(x2+y2)
= (x2)2-(y2)2
= x4-y4
只有符合平方差公式特征的代数式才能用平方差公式,要准确找到公式中的a、b.
例题示范
( )
( )
( )
×
×
判断下列各式是否正确,并说明理由:
( )
√
( )
×
×
a2
1-9x2
x2+xy-6y2
-a2+2ab-b2
2、利用平方差公式简便计算: 199.8×200.2
解:
199.8×200.2
= (200-0.2)(200+0.2)
= 2002-0.22
= 40000-0.04
= 39999.96
现在你知道张威是怎么计算的吧
3、小聪和小明用同样长度的细铁丝
围成一个长方形.小聪认为围成一个
正方形可使面积最大,而小明认为不一定.你认为呢?说说你的道理吧.
解:
小聪的说法正确.
理由如下:
设铁丝总长为4x厘米.
若围成正方形,则正方形的边长为x厘米,面积为x2平方厘米;
若围成相邻两边不相等的长方形,设长方形的较短一边长为(x-a)厘米,则较长一边长为(x+a)厘米,面积为(x+a)(x-a)=(x2-a2)平方厘米.显然x2>x2-a2,所以围成一个正方形可使面积最大.
(1)(a+1)(a-1)= . (2)(2n-3)(2n+3)= .
(3)(-x-2)(-x+2)= . (4)(4y-3x)(-3x-4y)= .
(9)(x+1)(x-1)-x= .
(10)(x4+1)(x2+1)(x+1)(x-1)= .
(5)(ab-3)(ab+3)= . (6)(-51)×(-49) = .
(11)(x+y)( )=y2-x2.
(12)(-3x2-4y2)( )=16y4-9x4.
(7) = . (8) = .
快速抢答
3、已知a、b、c是三个连续的正整数,以b为边长作正方形,以a、c为相邻两边作长方形,哪个图形的面积大?大多少?
试求(2+1)(22+1)(24+1) (232+1)+1
的个位数字.
1、平方差公式:
2、注意问题:
①必须符合平方差公式特征的代数式才能用平方差公式;
②平方差公式可以逆用.
(a+b)(a-b)=a2-b2
可理解为:两个二项式相乘,若既有相同项又有相反项,则积为相同项的平方减去相反项的平方.
课堂小结
P32练习1—3题;P36习题12.3第1题.
课后作业
12.3.1两数和乘以这两数的差
教学目标
(1)理解和掌握平方差公式的特点;
(2)利用平方差公式进行多项式乘法的运算;
(3)通过小组合作、讨论,培养学生实际动手操作能力和与人交流、分享的人际关系;
(4)感受数形结合思想和建模思想解决数学问题的重要性;
(5)感知公式体现的数学美;
(6)体会从前后一致,逻辑连贯的数学演化思维以及从一般到特殊,再从特殊回归一般的事物本质;
张威同学去商店买单价是9.8元/千克的糖块10.2千克,售货员刚拿起计算器,张威就说出应付99.96元,结果与售货员计算出的结果相吻合。售货员惊讶地问:“这位同学,你怎么算得这么快 ”张威同学说:“我用了在数学课上刚学过的一个公式。”你知道张威同学用的是一个什么样的公式吗 学了本节后,你就能解决这个问题了。
情景导入
3.计算:
(1)(x+3)(x-3); (2)(a+2b)(a-2b);
(3)(4m+n)(4m-n); (4)(5+4y)(5-4y)。
1.多项式乘以多项式的法则:_______。
2.利用多项式与多项式的乘法法则说出
(x+a)(x+b)的结果。
(x+a)(x+b)=x2+(a+b)x+ab
温故知新
相互检查,交流心得
(x+3)(x-3)
(a+2b)(a-2b)
(4m+n)(4m-n)
(5+4y)(5-4y)
观察两个多项式的特征,再看看结果和这两个多项式各项的关系:
x2-9
a2-4b2
16m2-n2
25-16y2
a2-b2
(a+b)(a-b)
探索新知
(a+b)(a-b) a b a2-b2 结果
(y+3)(y-3)
(2m-n)(2m+n)
(-x+2)(-x-2)
(1-5b)(5b+1)
(-2x-3y)(-3y+2x)
找一找:
y2-32
y
3
y2-9
2m
n
(2m)2-n2
4m2-n2
-x
2
(-x)2-22
x2-4
1
5b
12-(5b)2
1-25b2
-3y
2x
(-3y)2-(2x)2
可以用多项式的乘法法则验证结果的正确性哟!
9y2-4x2
用字母表示为:
这个公式叫两数和与这两数差的乘法公式,简称为平方差公式.
注:必须符合平方差公式特征的 代数式才能用平方差公式.
两数的和与这两数的差之积,
等于这两数的平方差.
(a+b)(a-b)=a2-b2
等式左边是两个数(字母)的和乘以这两个数(字母)的差.
等式右边是这两个数(字母)的平方差.
你能说出平方差公式的几何意义吗?(即用图形面积来解释这个公式)
a
a
b
(a+b)(a-b)
a
a-b
b
a2
-b2
=
用图形面积解释公式,
这就是数形结合的思想.
表示长为(a+b)、宽为(a-b)的矩形面积等于边长为a、b的两正方形面积之差.
a2
b2
1、计算:
(1)(a+5)(5-a);
(2)(2a2-3b)(2a2+3b);
解:(1)原式=52-a2
=25-a2
(2)原式=(2a2)2-(3b)2
=4a4-9b2
(3)a(a-5)-(a+6)(a-6); (4)(x-y)(x+y)(x2+y2).
解: a(a-5)-(a+6)(a-6)
= a2-5a-(a2-62)
= a2-5a-a2+36
= -5a+36
解: (x-y)(x+y)(x2+y2)
= (x2-y2)(x2+y2)
= (x2)2-(y2)2
= x4-y4
只有符合平方差公式特征的代数式才能用平方差公式,要准确找到公式中的a、b.
例题示范
( )
( )
( )
×
×
判断下列各式是否正确,并说明理由:
( )
√
( )
×
×
a2
1-9x2
x2+xy-6y2
-a2+2ab-b2
2、利用平方差公式简便计算: 199.8×200.2
解:
199.8×200.2
= (200-0.2)(200+0.2)
= 2002-0.22
= 40000-0.04
= 39999.96
现在你知道张威是怎么计算的吧
3、小聪和小明用同样长度的细铁丝
围成一个长方形.小聪认为围成一个
正方形可使面积最大,而小明认为不一定.你认为呢?说说你的道理吧.
解:
小聪的说法正确.
理由如下:
设铁丝总长为4x厘米.
若围成正方形,则正方形的边长为x厘米,面积为x2平方厘米;
若围成相邻两边不相等的长方形,设长方形的较短一边长为(x-a)厘米,则较长一边长为(x+a)厘米,面积为(x+a)(x-a)=(x2-a2)平方厘米.显然x2>x2-a2,所以围成一个正方形可使面积最大.
(1)(a+1)(a-1)= . (2)(2n-3)(2n+3)= .
(3)(-x-2)(-x+2)= . (4)(4y-3x)(-3x-4y)= .
(9)(x+1)(x-1)-x= .
(10)(x4+1)(x2+1)(x+1)(x-1)= .
(5)(ab-3)(ab+3)= . (6)(-51)×(-49) = .
(11)(x+y)( )=y2-x2.
(12)(-3x2-4y2)( )=16y4-9x4.
(7) = . (8) = .
快速抢答
3、已知a、b、c是三个连续的正整数,以b为边长作正方形,以a、c为相邻两边作长方形,哪个图形的面积大?大多少?
试求(2+1)(22+1)(24+1) (232+1)+1
的个位数字.
1、平方差公式:
2、注意问题:
①必须符合平方差公式特征的代数式才能用平方差公式;
②平方差公式可以逆用.
(a+b)(a-b)=a2-b2
可理解为:两个二项式相乘,若既有相同项又有相反项,则积为相同项的平方减去相反项的平方.
课堂小结
P32练习1—3题;P36习题12.3第1题.
课后作业
