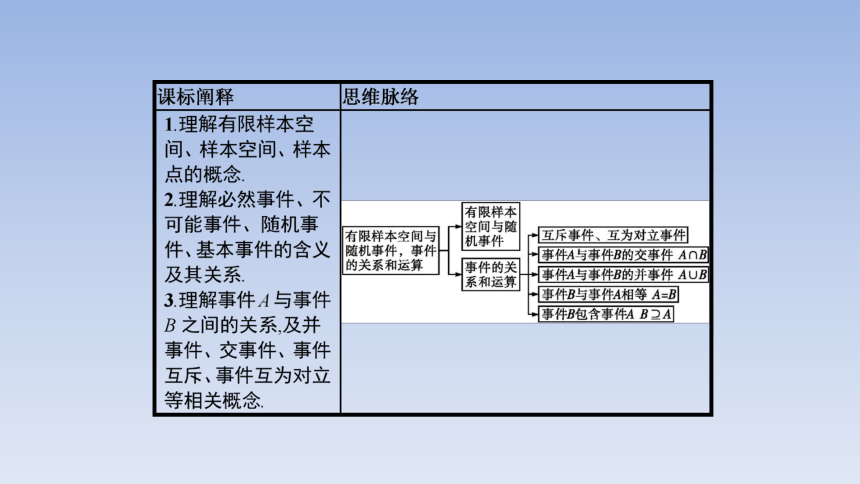
高中数学人教A版2019必修第二册 课件10.1.1 有限样本空间与随机事件 10.1.2 事件的关系和运算(共39张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 课件10.1.1 有限样本空间与随机事件 10.1.2 事件的关系和运算(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 689.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 20:45:47 | ||
图片预览










文档简介
(共39张PPT)
10.1.1 有限样本空间与随机事件
10.1.2 事件的关系和运算
一
二
三
一、有限样本空间的相关概念
1.抛掷两枚骰子,观察它们落地时朝上面的点数情况,你能写出该试验的样本空间吗
提示可以考虑用有序数对(a,b)来表示试验的结果.其中a表示其中一枚骰子的点数,b表示另一枚骰子的点数,则有Ω={(a,b)|1≤a≤6,1≤b≤6,且a,b∈N*},当然Ω还可以用列举法进行表示,该空间中有36个样本点.
一
二
三
2.填空
(1)随机试验:我们把对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母E表示.
说明:本节中我们研究的是具有以下特点的随机试验.
①试验可以在相同条件下重复进行;
②试验的所有可能结果是明确可知的,并且不止一个;
③每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
(2)样本点:随机试验E的每个可能的基本结果称为样本点.
(3)样本空间:全体样本点的集合称为试验E的样本空间.
(4)有限样本空间:
一般地,我们用Ω表示样本空间,用ω表示样本点.如果一个试验有n个可能结果,ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间,也就是说Ω为有限集的情况即为有限样本空间.
一
二
三
3.做一做
袋中装有大小相同的红、白、黄、黑4个球,分别写出以下随机试验的条件和结果.
(1)从中任取1球;
(2)从中任取2球.
解:(1)条件为:从袋中任取1球,结果为:红、白、黄、黑4种.
(2)条件为:从袋中任取2球.若记(红,白)表示一次试验中取出的是红球与白球,结果为:(红,白),(红,黄),(红,黑),(白,黄),(白,黑),(黄,黑)6种.
一
二
三
二、事件的概念及分类
1.思考
(1)考察下列事件:①导体通电时发热;②向上抛出的石头会下落;③在标准大气压下,水温升高到100 ℃会沸腾.这些事件就其发生与否有什么共同特点
提示都是必然会发生的事件.
(2)考察下列事件:①在没有水分的真空中种子发芽;②在常温常压下钢铁熔化;③一个三角形的大边所对的角小,小边所对的角大.这些事件就其发生与否有什么共同特点
提示都是不可能发生的事件.
(3)考察下列事件:①某人射击一次,命中目标;②某人购买福利彩票中奖;③抛掷一枚质地均匀的骰子出现的点数为偶数.这些事件就其发生与否有什么共同特点
提示都是可能发生也可能不发生的事件.
一
二
三
2.填空
(1)随机事件:样本空间Ω的子集称为随机事件,简称事件.
(2)基本事件:只包含一个样本点的事件称为基本事件.
(3)事件A发生:在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
(4)必然事件:Ω作为自身的子集,包含了所有的样本点,在每次试验中总有一个样本点发生,所以Ω总会发生,我们称Ω为必然事件.
(5)不可能事件:空间 不包含任何样本点,在每次试验中都不会发生,我们称 为不可能事件.
说明:(1)每个事件都是样本空间Ω的一个子集.
(2)为了统一处理,将必然事件和不可能事件作为随机事件的两个极端情形.
一
二
三
3.做一做
(1)已知集合A是集合B的真子集,则下列关于非空集合A,B的四个命题:
①若任取x∈A,则x∈B是必然事件;
②若任取x A,则x∈B是不可能事件;
③若任取x∈B,则x∈A是随机事件;
④若任取x B,则x A是必然事件.
其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
答案:C
解析:∵集合A是集合B的真子集,∴A中的任意一个元素都是B中的元素,而B中至少有一个元素不在A中,因此①正确,②错误,③正确,④正确.
一
二
三
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①从集合的角度看,事件 与事件Ω的关系为 Ω.( )
②必然事件也可能不发生,不可能事件一定不能发生.( )
③只有当A中的样本点都发生了,事件A才发生.( )
答案:①√ ②× ③×
一
二
三
三、利用集合的知识研究随机事件
1.思考
对于随机事件A,B之间的关系可以用如下图示来刻划,你能用集合符号表示下列图示吗
一
二
三
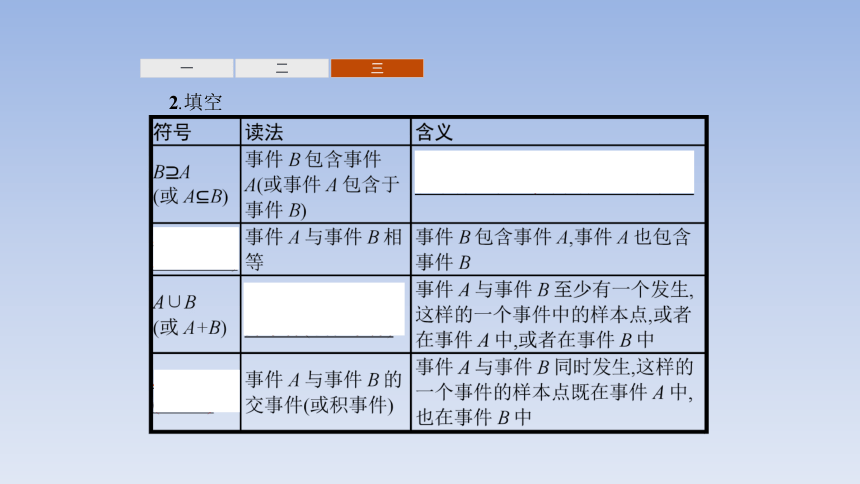
2.填空
一
二
三
一
二
三
3.做一做
(1)掷一颗骰子,统计正面向上的点数.
记“出现5点”=A,“出现3点”=B,“出现1点”=C,
则“出现奇数点”这一事件可表示为 .事件A∪B与事件C是否互为对立事件, (填“是”或“否”).
答案:A∪B∪C 否
(2)有甲、乙两台机床,记“甲正常工作”=A,“乙正常工作”=B,则AB表示 ,“甲不能正常工作”可记为 .
答案:“甲、乙同时正常工作”
一
二
三
(3)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①事件A发生,事件B与C不发生,则可表示为AB C.( )
②事件A,B,C均不发生可表示为A B C.( )
③事件A,B,C至少有两个发生可表示为A∪B∪C.( )
④若事件A与B是互为对立事件,则事件A与B一定为互斥事件.( )
答案:①√ ②√ ③× ④√
探究一
探究二
探究三
探究四
思维辨析
随堂演练
试验的样本空间
例1某人做试验,从一个装有标号为1,2,3,4的小球的盒子中,无放回地取两个小球,每次取一个,先取的小球的标号为x,后取的小球的标号为y,这样构成有序实数对(x,y).
(1)写出这个试验的样本空间;
(2)写出“第一次取出的小球上的标号为2”这一事件.
分析利用列举法按照一定的顺序逐个列举即可.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)当x=1时,y=2,3,4;
当x=2时,y=1,3,4;
当x=3时,y=1,2,4;
当x=4时,y=1,2,3.因此,这个试验的样本空间是Ω={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)}.
(2)记“第一次取出的小球上的标号为2”为事件A,则A={(2,1),(2,3),(2,4)}.
反思感悟 随机事件的结果是相对于条件而言的,要弄清某一随机事件的结果,首先必须明确事件发生的条件.在写试验结果时,要按照一定的顺序采用列举法写出,注意不能重复也不能遗漏.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
延伸探究1若将本例中的条件改为有放回地取两个小球呢 每次取一个,先取的小球的标号为x,看清编号后放回盒子摇匀,再取一个小球的标号为y,这样构成有序实数对(x,y).试写出这个试验的样本空间.
解:当x=1时,y可取1,2,3,4.
同理,x=2,3,4时,对应的不同的试验结果也有4个.
所以这个试验的样本空间为Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
延伸探究2若将本例中的条件改为无放回地取三个小球呢 每次取一个,先取的小球的标号为x,后取的小球的标号为y,最后取的小球的标号为z,这样构成有序实数对(x,y,z).试写出这个试验的样本空间.
解:当x=1时,y可取2,3,4.
若y=2,则z可取3,4;
若y=3,则z可取2,4;
若y=4,则z可取2,3.
同理,x=2,3,4时,对应的不同的试验结果也有6个.
所以,这个试验的样本空间是
Ω={(1,2,3),(1,2,4),(1,3,2),(1,3,4),(1,4,2),(1,4,3),(2,1,3),(2,1,4),(2,3,1),(2,3,4),(2,4,1),(2,4,3),(3,1,2),(3,1,4),(3,2,1),(3,2,4),(3,4,2),(3,4,1),(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,2),(4,3,1)}.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
随机事件的概念及分类
例2(1)以下的随机事件中不是必然事件的是( )
A.标准大气压下,水加热到100 ℃,必会沸腾
B.长和宽分别为a,b的矩形,其面积为a×b
C.走到十字路口,遇到红灯
D.三角形内角和为180°
(2)下列事件中,是必然事件的是( )
A.任意买一张电影票,座位号是2的倍数
B.12个人中有两个人生肖相同
C.买了一注彩票中一等奖
D.实数a+b=b+a
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:(1)C (2)D
解析:(1)在A中,标准大气压下,水加热到100 ℃,必会沸腾是必然事件,故A不符合题意;在B中,长和宽分别为a,b的矩形,其面积为a×b是必然事件,故B不符合题意;在C中,走到十字路口,遇到红灯是随机事件但不是必然事件,故C符合题意;在D中,三角形内角和为180°是必然事件,故D不符合题意.
(2)四个选项都是随机事件,但选项A,B,C中的事件都不确定发生,因此都不是必然事件,只有选项D总会发生,因此是必然事件.
反思感悟 (1)要判断一个事件是必然事件、随机事件、还是不可能事件,要从定义出发.
(2)必然事件和不可能事件不具有随机性,但为了统一处理,将必然事件和不可能事件作为随机事件的特殊情形,具有随机性的和不具有随机性的事件都可以理论上认为是随机事件。
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练1从6个篮球、2个排球中任选3个球,则下列事件中,不可能事件是( )
A.3个都是篮球 B.至少有1个是排球
C.3个都是排球 D.至少有1个是篮球
答案:C
解析:根据题意,从6个篮球、2个排球中任选3个球,四个选项都是随机事件,进一步C是不可能事件,D是必然事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
互斥事件、对立事件的判断
例3把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
分析由题意可知事件“甲分得红牌”与“乙分得红牌”不会同时发生,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”和“丁分得红牌”,则两者不是对立事件.
答案:B
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解析:根据题意,把红、黄、蓝、白四张纸牌随机分给甲、乙、丙、丁四个人,
事件“甲分得红牌”与“乙分得红牌”不会同时发生,则两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”和“丁分得红牌”,则两者不是对立事件.
∴事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件.故选B.
反思感悟 一般判断互斥事件或对立事件从集合的角度来认识,若A∪B=Ω,A∩B= ,则称A与B互为对立;若A∩B= ,则称A与B为互斥(互不相容).对于本例中的问题, 要把样本空间明确,再进行分析.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练2从装有3个红球和2个白球的口袋中随机取出3个球,则事件“取出1个红球和2个白球”的对立事件是( )
A.取出2个红球和1个白球
B.取出的3个球全是红球
C.取出的3个球中既有红球也有白球
D.取出的3个球中不止一个红球
答案:D
解析:从装有3个红球和2个白球的口袋中随机取出3个球,则事件“取出1个红球和2个白球”的对立事件是取出的3个球中至少有两个红球.故选D.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
用简单事件的和或积表示复杂事件
例4已知电路图 ,其中记A1=“开关K1合上”,A2=“开关K2合上”.则A1A2表示的含义是 .
答案:“开关K1,K2同时合上”这一事件
探究一
探究二
探究三
探究四
思维辨析
随堂演练
例5盒子里有6个红球,4个白球,现从中任取3个球,设事件A=“3个球中有1个红球,2个白球”,事件B=“3个球中有2个红球,1个白球”,事件C=“3个球中至少有1个红球”,事件D=“3个球中既有红球又有白球”.问:
(1)事件D与A,B是什么样的运算关系
(2)事件C与A的交事件是什么事件
分析事件间运算的类型:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)对于事件D,可能的结果为1个红球2个白球或2个红球1个白球,故D=A∪B.
(2)对于事件C,可能的结果为1个红球2个白球,2个红球1个白球,3个均为红球,故C∩A=A.
反思感悟 进行事件运算时应注意的问题
(1)进行事件的运算时,一是要紧扣运算的定义,二是要全面考查同一条件下的试验可能出现的全部结果,必要时可利用Venn图或列出全部的试验结果进行分析.
(2)在一些比较简单的题目中,需要判断事件之间的关系时,可以根据常识来判断.但如果遇到比较复杂的题目,就得严格按照事件之间关系的定义来推理.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练3在掷质地均匀的骰子的试验中,可以定义许多事件.例如:
C1=“出现1点”,C2=“出现2点”,C3=“出现3点”,
C4=“出现4点”,C5=“出现5点”,C6=“出现6点”,
D1=“出现的点数不大于1”,D2=“出现的点数大于3”,
D3=“出现的点数小于5”,E=“出现的点数小于7”,
F=“出现的点数为偶数”,G=“出现的点数为奇数”,
请根据上述定义的事件,回答下列问题.
(1)请列出事件D2,事件F包含的事件及符合相等关系的事件;
(2)利用和事件的定义,判断上述哪些事件是和事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)事件D2包含事件C4,C5,C6.事件F包含事件C2,C4,C6.事件C1与事件D1相等,即C1=D1.
(2)因为D2=“出现的点数大于3”=“出现4点或出现5点或出现6点”,所以D2=C4∪C5∪C6,所以事件D2为和事件.同理可得事件D3,事件E,事件F,事件G均为和事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练4从一批100件的产品中每次取出一个(取后不放回),假设100件产品中有5件是次品,用事件Ak表示第k次取到次品(k=1,2,3),试用A1,A2,A3表示下列事件.
(1)三次全取到次品.
(2)只有第一次取到次品.
(3)三次中至少有一次取到次品.
(4)三次中恰有两次取到次品.
(5)三次中至多有一次取到次品.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
忽略试验的顺序导致试验结果出错
典例先后抛掷两枚质地均匀的硬币,则:
(1)一共可能出现多少种不同的结果
(2)出现“一枚正面,另一枚反面”的情况有几种
错解(1)一共出现“两枚正面”“两枚反面”“一枚正面,一枚反面”3种情况.
(2)出现“一枚正面,另一枚反面”的情况只有1种.
以上错解中都有哪些错误 出错的原因是什么 你如何订正 你如何防范
错因分析将“一正、一反”“一反、一正”两种情形错认为是一种情形.在题干中若强调了“先后”“依次”“顺序”“前后”,则必须注意顺序问题.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
正解(1)一共可能出现“两枚正面”“两枚反面”“一枚正面,一枚反面”“一枚反面,一枚正面”4种不同的结果.
(2)出现“一枚正面,另一枚反面”的情况有2种.
防范措施 1.把握随机试验的实质,明确一次试验的含义.
2.按一定的顺序用有序数组的形式写出,要不重不漏.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练一个家庭有两个小孩儿,则可能的结果为( )
A.{(男,女),(男,男),(女,女)}
B.{(男,女),(女,男)}
C.{(男,男),(男,女),(女,男),(女,女)}
D.{(男,男),(女,女)}
答案:C
解析:随机试验的所有结果要保证等可能性.两小孩儿有大小之分,所以(男,女)与(女,男)是不同的结果,故选C.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
1.(多选)下列事件中,是随机事件的有( )
A.在学校运动会上,学生张涛获得100 m短跑冠军
B.在体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李凯
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.在标准大气压下,水在4 ℃时结冰
分析利用随机事件的概念直接判断.
答案:ABCD
解析:在A中,在学校运动会上,学生张涛获得100 m短跑冠军,是随机事件;
在B中,在体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李凯,是随机事件;
在C中,从标有1,2,3,4的4张号签中任取一张,恰为1号签,是随机事件;
在D中,在标准大气压下,水在4 ℃时结冰是不可能事件.也属于随机事件的特殊情况.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
2.抽查10件产品,设“至少抽到2件次品”为事件A,则A的对立事件是( )
A.至多抽到2件次品 B.至多抽到2件正品
C.至少抽到2件正品 D.至多抽到一件次品
答案:D
解析:抽查10件产品,设“至少抽到2件次品”为事件A,则 为至多抽到一件次品.故选D.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
3.一箱产品中有正品4件,次品3次,从中任取2件,下列四组事件:
①恰有一件次品和恰有两件次品;②至少有一件次品和全是次品;③至少有一件正品和至少有一件次品;④至少有一件次品和全是正品.其中两个事件互斥的是 .(填序号)
答案:①④
解析:∵从一箱产品中任取2件,观察正品件数和次品件数,其中正品、次品都多于2件,
∴恰有一件次品和恰有两件次品是互斥的,至少有一件次品和全是正品是互斥的,∴①④是互斥事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
4.(多空题)如图所示,事件A=“甲元件正常”,B=“乙元件正常”,C=“丙元件正常”.则A∪B∪C表示的含义为 , 表示的含义为 .
答案:电路工作正常 电路工作不正常
探究一
探究二
探究三
探究四
思维辨析
随堂演练
5.给出下列四个命题:
①集合{x||x|<0}为空集是必然事件;
②y=f(x)是奇函数,则f(0)=0是随机事件;
③若loga(x-1)>0,则x>1是必然事件;
④对顶角不相等是不可能事件.
其中正确命题是 .
答案:①②③④
解析:∵|x|≥0恒成立,∴①正确;奇函数y=f(x)只有当x=0有意义时才有f(0)=0,∴②正确;由loga(x-1)>0知,当a>1时,x-1>1即x>2;当0探究一
探究二
探究三
探究四
思维辨析
随堂演练
6.设集合M={1,2,3,4},a∈M,b∈M,(a,b)是一个基本事件.
(1)“a+b=5”这一事件包含哪几个基本事件 “a<3且b>1”呢
(2)“ab=4”这一事件包含哪几个基本事件 “a=b”呢
解:这个试验的基本事件构成集合Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.
(1)“a+b=5”这一事件包含以下4个基本事件:(1,4),(2,3),(3,2),(4,1).
“a<3且b>1”这一事件包含以下6个基本事件:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).
(2)“ab=4”这一事件包含以下3个基本事件:(1,4),(2,2),(4,1);
“a=b”这一事件包含以下4个基本事件:(1,1),(2,2),(3,3),(4,4).
10.1.1 有限样本空间与随机事件
10.1.2 事件的关系和运算
一
二
三
一、有限样本空间的相关概念
1.抛掷两枚骰子,观察它们落地时朝上面的点数情况,你能写出该试验的样本空间吗
提示可以考虑用有序数对(a,b)来表示试验的结果.其中a表示其中一枚骰子的点数,b表示另一枚骰子的点数,则有Ω={(a,b)|1≤a≤6,1≤b≤6,且a,b∈N*},当然Ω还可以用列举法进行表示,该空间中有36个样本点.
一
二
三
2.填空
(1)随机试验:我们把对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母E表示.
说明:本节中我们研究的是具有以下特点的随机试验.
①试验可以在相同条件下重复进行;
②试验的所有可能结果是明确可知的,并且不止一个;
③每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
(2)样本点:随机试验E的每个可能的基本结果称为样本点.
(3)样本空间:全体样本点的集合称为试验E的样本空间.
(4)有限样本空间:
一般地,我们用Ω表示样本空间,用ω表示样本点.如果一个试验有n个可能结果,ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间,也就是说Ω为有限集的情况即为有限样本空间.
一
二
三
3.做一做
袋中装有大小相同的红、白、黄、黑4个球,分别写出以下随机试验的条件和结果.
(1)从中任取1球;
(2)从中任取2球.
解:(1)条件为:从袋中任取1球,结果为:红、白、黄、黑4种.
(2)条件为:从袋中任取2球.若记(红,白)表示一次试验中取出的是红球与白球,结果为:(红,白),(红,黄),(红,黑),(白,黄),(白,黑),(黄,黑)6种.
一
二
三
二、事件的概念及分类
1.思考
(1)考察下列事件:①导体通电时发热;②向上抛出的石头会下落;③在标准大气压下,水温升高到100 ℃会沸腾.这些事件就其发生与否有什么共同特点
提示都是必然会发生的事件.
(2)考察下列事件:①在没有水分的真空中种子发芽;②在常温常压下钢铁熔化;③一个三角形的大边所对的角小,小边所对的角大.这些事件就其发生与否有什么共同特点
提示都是不可能发生的事件.
(3)考察下列事件:①某人射击一次,命中目标;②某人购买福利彩票中奖;③抛掷一枚质地均匀的骰子出现的点数为偶数.这些事件就其发生与否有什么共同特点
提示都是可能发生也可能不发生的事件.
一
二
三
2.填空
(1)随机事件:样本空间Ω的子集称为随机事件,简称事件.
(2)基本事件:只包含一个样本点的事件称为基本事件.
(3)事件A发生:在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
(4)必然事件:Ω作为自身的子集,包含了所有的样本点,在每次试验中总有一个样本点发生,所以Ω总会发生,我们称Ω为必然事件.
(5)不可能事件:空间 不包含任何样本点,在每次试验中都不会发生,我们称 为不可能事件.
说明:(1)每个事件都是样本空间Ω的一个子集.
(2)为了统一处理,将必然事件和不可能事件作为随机事件的两个极端情形.
一
二
三
3.做一做
(1)已知集合A是集合B的真子集,则下列关于非空集合A,B的四个命题:
①若任取x∈A,则x∈B是必然事件;
②若任取x A,则x∈B是不可能事件;
③若任取x∈B,则x∈A是随机事件;
④若任取x B,则x A是必然事件.
其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
答案:C
解析:∵集合A是集合B的真子集,∴A中的任意一个元素都是B中的元素,而B中至少有一个元素不在A中,因此①正确,②错误,③正确,④正确.
一
二
三
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①从集合的角度看,事件 与事件Ω的关系为 Ω.( )
②必然事件也可能不发生,不可能事件一定不能发生.( )
③只有当A中的样本点都发生了,事件A才发生.( )
答案:①√ ②× ③×
一
二
三
三、利用集合的知识研究随机事件
1.思考
对于随机事件A,B之间的关系可以用如下图示来刻划,你能用集合符号表示下列图示吗
一
二
三
2.填空
一
二
三
一
二
三
3.做一做
(1)掷一颗骰子,统计正面向上的点数.
记“出现5点”=A,“出现3点”=B,“出现1点”=C,
则“出现奇数点”这一事件可表示为 .事件A∪B与事件C是否互为对立事件, (填“是”或“否”).
答案:A∪B∪C 否
(2)有甲、乙两台机床,记“甲正常工作”=A,“乙正常工作”=B,则AB表示 ,“甲不能正常工作”可记为 .
答案:“甲、乙同时正常工作”
一
二
三
(3)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①事件A发生,事件B与C不发生,则可表示为AB C.( )
②事件A,B,C均不发生可表示为A B C.( )
③事件A,B,C至少有两个发生可表示为A∪B∪C.( )
④若事件A与B是互为对立事件,则事件A与B一定为互斥事件.( )
答案:①√ ②√ ③× ④√
探究一
探究二
探究三
探究四
思维辨析
随堂演练
试验的样本空间
例1某人做试验,从一个装有标号为1,2,3,4的小球的盒子中,无放回地取两个小球,每次取一个,先取的小球的标号为x,后取的小球的标号为y,这样构成有序实数对(x,y).
(1)写出这个试验的样本空间;
(2)写出“第一次取出的小球上的标号为2”这一事件.
分析利用列举法按照一定的顺序逐个列举即可.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)当x=1时,y=2,3,4;
当x=2时,y=1,3,4;
当x=3时,y=1,2,4;
当x=4时,y=1,2,3.因此,这个试验的样本空间是Ω={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)}.
(2)记“第一次取出的小球上的标号为2”为事件A,则A={(2,1),(2,3),(2,4)}.
反思感悟 随机事件的结果是相对于条件而言的,要弄清某一随机事件的结果,首先必须明确事件发生的条件.在写试验结果时,要按照一定的顺序采用列举法写出,注意不能重复也不能遗漏.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
延伸探究1若将本例中的条件改为有放回地取两个小球呢 每次取一个,先取的小球的标号为x,看清编号后放回盒子摇匀,再取一个小球的标号为y,这样构成有序实数对(x,y).试写出这个试验的样本空间.
解:当x=1时,y可取1,2,3,4.
同理,x=2,3,4时,对应的不同的试验结果也有4个.
所以这个试验的样本空间为Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
延伸探究2若将本例中的条件改为无放回地取三个小球呢 每次取一个,先取的小球的标号为x,后取的小球的标号为y,最后取的小球的标号为z,这样构成有序实数对(x,y,z).试写出这个试验的样本空间.
解:当x=1时,y可取2,3,4.
若y=2,则z可取3,4;
若y=3,则z可取2,4;
若y=4,则z可取2,3.
同理,x=2,3,4时,对应的不同的试验结果也有6个.
所以,这个试验的样本空间是
Ω={(1,2,3),(1,2,4),(1,3,2),(1,3,4),(1,4,2),(1,4,3),(2,1,3),(2,1,4),(2,3,1),(2,3,4),(2,4,1),(2,4,3),(3,1,2),(3,1,4),(3,2,1),(3,2,4),(3,4,2),(3,4,1),(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,2),(4,3,1)}.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
随机事件的概念及分类
例2(1)以下的随机事件中不是必然事件的是( )
A.标准大气压下,水加热到100 ℃,必会沸腾
B.长和宽分别为a,b的矩形,其面积为a×b
C.走到十字路口,遇到红灯
D.三角形内角和为180°
(2)下列事件中,是必然事件的是( )
A.任意买一张电影票,座位号是2的倍数
B.12个人中有两个人生肖相同
C.买了一注彩票中一等奖
D.实数a+b=b+a
探究一
探究二
探究三
探究四
思维辨析
随堂演练
答案:(1)C (2)D
解析:(1)在A中,标准大气压下,水加热到100 ℃,必会沸腾是必然事件,故A不符合题意;在B中,长和宽分别为a,b的矩形,其面积为a×b是必然事件,故B不符合题意;在C中,走到十字路口,遇到红灯是随机事件但不是必然事件,故C符合题意;在D中,三角形内角和为180°是必然事件,故D不符合题意.
(2)四个选项都是随机事件,但选项A,B,C中的事件都不确定发生,因此都不是必然事件,只有选项D总会发生,因此是必然事件.
反思感悟 (1)要判断一个事件是必然事件、随机事件、还是不可能事件,要从定义出发.
(2)必然事件和不可能事件不具有随机性,但为了统一处理,将必然事件和不可能事件作为随机事件的特殊情形,具有随机性的和不具有随机性的事件都可以理论上认为是随机事件。
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练1从6个篮球、2个排球中任选3个球,则下列事件中,不可能事件是( )
A.3个都是篮球 B.至少有1个是排球
C.3个都是排球 D.至少有1个是篮球
答案:C
解析:根据题意,从6个篮球、2个排球中任选3个球,四个选项都是随机事件,进一步C是不可能事件,D是必然事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
互斥事件、对立事件的判断
例3把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
分析由题意可知事件“甲分得红牌”与“乙分得红牌”不会同时发生,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”和“丁分得红牌”,则两者不是对立事件.
答案:B
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解析:根据题意,把红、黄、蓝、白四张纸牌随机分给甲、乙、丙、丁四个人,
事件“甲分得红牌”与“乙分得红牌”不会同时发生,则两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”和“丁分得红牌”,则两者不是对立事件.
∴事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件.故选B.
反思感悟 一般判断互斥事件或对立事件从集合的角度来认识,若A∪B=Ω,A∩B= ,则称A与B互为对立;若A∩B= ,则称A与B为互斥(互不相容).对于本例中的问题, 要把样本空间明确,再进行分析.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练2从装有3个红球和2个白球的口袋中随机取出3个球,则事件“取出1个红球和2个白球”的对立事件是( )
A.取出2个红球和1个白球
B.取出的3个球全是红球
C.取出的3个球中既有红球也有白球
D.取出的3个球中不止一个红球
答案:D
解析:从装有3个红球和2个白球的口袋中随机取出3个球,则事件“取出1个红球和2个白球”的对立事件是取出的3个球中至少有两个红球.故选D.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
用简单事件的和或积表示复杂事件
例4已知电路图 ,其中记A1=“开关K1合上”,A2=“开关K2合上”.则A1A2表示的含义是 .
答案:“开关K1,K2同时合上”这一事件
探究一
探究二
探究三
探究四
思维辨析
随堂演练
例5盒子里有6个红球,4个白球,现从中任取3个球,设事件A=“3个球中有1个红球,2个白球”,事件B=“3个球中有2个红球,1个白球”,事件C=“3个球中至少有1个红球”,事件D=“3个球中既有红球又有白球”.问:
(1)事件D与A,B是什么样的运算关系
(2)事件C与A的交事件是什么事件
分析事件间运算的类型:
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)对于事件D,可能的结果为1个红球2个白球或2个红球1个白球,故D=A∪B.
(2)对于事件C,可能的结果为1个红球2个白球,2个红球1个白球,3个均为红球,故C∩A=A.
反思感悟 进行事件运算时应注意的问题
(1)进行事件的运算时,一是要紧扣运算的定义,二是要全面考查同一条件下的试验可能出现的全部结果,必要时可利用Venn图或列出全部的试验结果进行分析.
(2)在一些比较简单的题目中,需要判断事件之间的关系时,可以根据常识来判断.但如果遇到比较复杂的题目,就得严格按照事件之间关系的定义来推理.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练3在掷质地均匀的骰子的试验中,可以定义许多事件.例如:
C1=“出现1点”,C2=“出现2点”,C3=“出现3点”,
C4=“出现4点”,C5=“出现5点”,C6=“出现6点”,
D1=“出现的点数不大于1”,D2=“出现的点数大于3”,
D3=“出现的点数小于5”,E=“出现的点数小于7”,
F=“出现的点数为偶数”,G=“出现的点数为奇数”,
请根据上述定义的事件,回答下列问题.
(1)请列出事件D2,事件F包含的事件及符合相等关系的事件;
(2)利用和事件的定义,判断上述哪些事件是和事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
解:(1)事件D2包含事件C4,C5,C6.事件F包含事件C2,C4,C6.事件C1与事件D1相等,即C1=D1.
(2)因为D2=“出现的点数大于3”=“出现4点或出现5点或出现6点”,所以D2=C4∪C5∪C6,所以事件D2为和事件.同理可得事件D3,事件E,事件F,事件G均为和事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练4从一批100件的产品中每次取出一个(取后不放回),假设100件产品中有5件是次品,用事件Ak表示第k次取到次品(k=1,2,3),试用A1,A2,A3表示下列事件.
(1)三次全取到次品.
(2)只有第一次取到次品.
(3)三次中至少有一次取到次品.
(4)三次中恰有两次取到次品.
(5)三次中至多有一次取到次品.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
忽略试验的顺序导致试验结果出错
典例先后抛掷两枚质地均匀的硬币,则:
(1)一共可能出现多少种不同的结果
(2)出现“一枚正面,另一枚反面”的情况有几种
错解(1)一共出现“两枚正面”“两枚反面”“一枚正面,一枚反面”3种情况.
(2)出现“一枚正面,另一枚反面”的情况只有1种.
以上错解中都有哪些错误 出错的原因是什么 你如何订正 你如何防范
错因分析将“一正、一反”“一反、一正”两种情形错认为是一种情形.在题干中若强调了“先后”“依次”“顺序”“前后”,则必须注意顺序问题.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
正解(1)一共可能出现“两枚正面”“两枚反面”“一枚正面,一枚反面”“一枚反面,一枚正面”4种不同的结果.
(2)出现“一枚正面,另一枚反面”的情况有2种.
防范措施 1.把握随机试验的实质,明确一次试验的含义.
2.按一定的顺序用有序数组的形式写出,要不重不漏.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
变式训练一个家庭有两个小孩儿,则可能的结果为( )
A.{(男,女),(男,男),(女,女)}
B.{(男,女),(女,男)}
C.{(男,男),(男,女),(女,男),(女,女)}
D.{(男,男),(女,女)}
答案:C
解析:随机试验的所有结果要保证等可能性.两小孩儿有大小之分,所以(男,女)与(女,男)是不同的结果,故选C.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
1.(多选)下列事件中,是随机事件的有( )
A.在学校运动会上,学生张涛获得100 m短跑冠军
B.在体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李凯
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.在标准大气压下,水在4 ℃时结冰
分析利用随机事件的概念直接判断.
答案:ABCD
解析:在A中,在学校运动会上,学生张涛获得100 m短跑冠军,是随机事件;
在B中,在体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李凯,是随机事件;
在C中,从标有1,2,3,4的4张号签中任取一张,恰为1号签,是随机事件;
在D中,在标准大气压下,水在4 ℃时结冰是不可能事件.也属于随机事件的特殊情况.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
2.抽查10件产品,设“至少抽到2件次品”为事件A,则A的对立事件是( )
A.至多抽到2件次品 B.至多抽到2件正品
C.至少抽到2件正品 D.至多抽到一件次品
答案:D
解析:抽查10件产品,设“至少抽到2件次品”为事件A,则 为至多抽到一件次品.故选D.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
3.一箱产品中有正品4件,次品3次,从中任取2件,下列四组事件:
①恰有一件次品和恰有两件次品;②至少有一件次品和全是次品;③至少有一件正品和至少有一件次品;④至少有一件次品和全是正品.其中两个事件互斥的是 .(填序号)
答案:①④
解析:∵从一箱产品中任取2件,观察正品件数和次品件数,其中正品、次品都多于2件,
∴恰有一件次品和恰有两件次品是互斥的,至少有一件次品和全是正品是互斥的,∴①④是互斥事件.
探究一
探究二
探究三
探究四
思维辨析
随堂演练
4.(多空题)如图所示,事件A=“甲元件正常”,B=“乙元件正常”,C=“丙元件正常”.则A∪B∪C表示的含义为 , 表示的含义为 .
答案:电路工作正常 电路工作不正常
探究一
探究二
探究三
探究四
思维辨析
随堂演练
5.给出下列四个命题:
①集合{x||x|<0}为空集是必然事件;
②y=f(x)是奇函数,则f(0)=0是随机事件;
③若loga(x-1)>0,则x>1是必然事件;
④对顶角不相等是不可能事件.
其中正确命题是 .
答案:①②③④
解析:∵|x|≥0恒成立,∴①正确;奇函数y=f(x)只有当x=0有意义时才有f(0)=0,∴②正确;由loga(x-1)>0知,当a>1时,x-1>1即x>2;当0
探究二
探究三
探究四
思维辨析
随堂演练
6.设集合M={1,2,3,4},a∈M,b∈M,(a,b)是一个基本事件.
(1)“a+b=5”这一事件包含哪几个基本事件 “a<3且b>1”呢
(2)“ab=4”这一事件包含哪几个基本事件 “a=b”呢
解:这个试验的基本事件构成集合Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.
(1)“a+b=5”这一事件包含以下4个基本事件:(1,4),(2,3),(3,2),(4,1).
“a<3且b>1”这一事件包含以下6个基本事件:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).
(2)“ab=4”这一事件包含以下3个基本事件:(1,4),(2,2),(4,1);
“a=b”这一事件包含以下4个基本事件:(1,1),(2,2),(3,3),(4,4).
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
