沪科版八年级上册数学13.1.1三角形中的边角关系 教案
文档属性
| 名称 | 沪科版八年级上册数学13.1.1三角形中的边角关系 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 20:36:00 | ||
图片预览

文档简介
13.1.三角形中的边角关系
1.三角形中边的关系
教学目标:
知识目标:理解三角形的有关概念,掌握三角形三边的关系。
能力目标:通过观察、操作、讨论等活动,培养学生的动手实践能力和语言表达能力。
情感目标:让学生在自主参与、合作交流的活动中,体验成功的喜悦,树立自信,激发学习数学的兴趣
教学重、难点
教学重点:三角形三边关系的探究和归纳
教学难点:三角形三边关系的应用
教学过程:
1、引入新课
形状似座山, 稳定性能坚, 三竿首位连,学问不简单。 (打一几何图形)
把事先收集的与三角形有关系的生活图片,运用投影仪播放,让学生对三角形有一个感性认识.
二、讲授新知:
三角形的定义
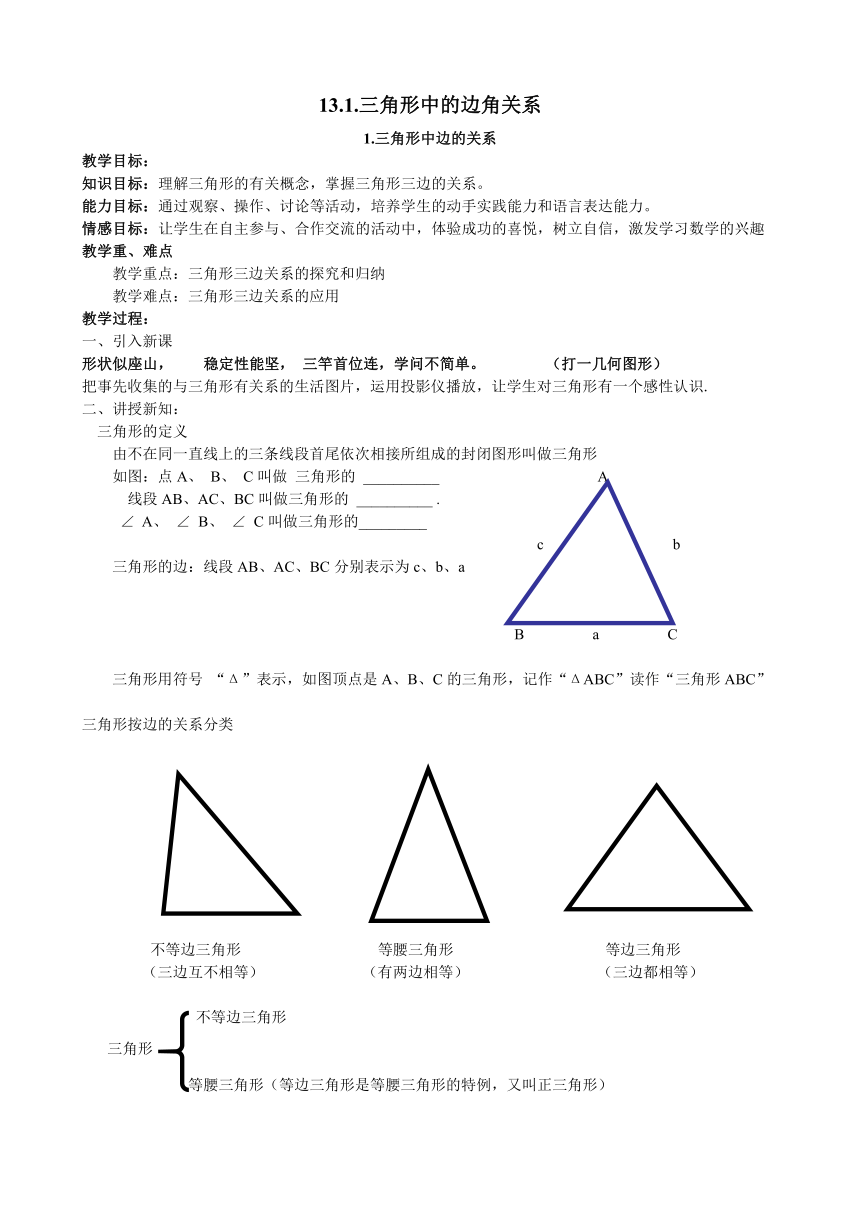
由不在同一直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形
如图:点A、 B、 C叫做 三角形的 __________ A
线段AB、AC、BC叫做三角形的 __________ .
∠ A、 ∠ B、 ∠ C叫做三角形的_________
c b
三角形的边:线段AB、AC、BC分别表示为c、b、a
B a C
三角形用符号 “Δ”表示,如图顶点是A、B、C的三角形,记作“ΔABC”读作“三角形ABC”
三角形按边的关系分类
不等边三角形 等腰三角形 等边三角形
(三边互不相等) (有两边相等) (三边都相等)
不等边三角形
等腰三角形(等边三角形是等腰三角形的特例,又叫正三角形)
等腰三角形各部分的名称
注意:腰、底边、顶角、底角等是相对于等腰三角形来说的,一般的三角形则不存在这些概念。
动动手
任意两边之和与第三边的大小 关系用不等式表示为:
思考:三角形的三边有怎样的关系?
猜想:三角形任何两边的和大于第三边!
理论验证:“两点之间的所有连线中,线段最短” AC+CB>AB
同理可得:AB+BC>AC, AB+AC>BC
三角形的三边关系:
1、 三角形中任何两边的和大于第三边
2、 三角形中任何两边的差小于第三边
对应练习:
下列长度的三条线段能否组成三角形?为什么?
(1) 2cm,3cm,4cm ( ) (2) 1cm,3cm,4cm ( )
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
解题技巧:只要比较两条较短线段之和与最长线段的大小
例题讲解:
例1:等腰三角形中,周长为18cm,
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长。
解:(1)设等腰三角形的底边长为xcm,根据题意,得
x+2x+2x=18
解方程,得
x=3.6
所以三角形的三边长为3.6cm,7.2cm,7.2cm
(2)若底边长为4cm,设腰长为xcm。根据题意,得
2x+4=18 解方程,得 x=7
若腰长为4cm,设底边长为xcm。根据题意,得
2×4+x=18 解方程,得 x=10
由于4+4<10,可知以4cm为腰长不能构成周长为18cm的等腰三角形。
所以,三角形的另两边长都是7cm
练习:
1.图中有几个三角形?分别是那几个?
2.若一个三角形三边长度之比为2:3:3,周长为16cm,则三角形的三边长分别是 , 这个三角形若按边分类是 .三角形
3.三角形中,已知两边长4cm和8cm,另一边长与前面的其中一边长相等,这个三角形的周长是 cm
三课堂小结
三角形
B
B
1.三角形中边的关系
教学目标:
知识目标:理解三角形的有关概念,掌握三角形三边的关系。
能力目标:通过观察、操作、讨论等活动,培养学生的动手实践能力和语言表达能力。
情感目标:让学生在自主参与、合作交流的活动中,体验成功的喜悦,树立自信,激发学习数学的兴趣
教学重、难点
教学重点:三角形三边关系的探究和归纳
教学难点:三角形三边关系的应用
教学过程:
1、引入新课
形状似座山, 稳定性能坚, 三竿首位连,学问不简单。 (打一几何图形)
把事先收集的与三角形有关系的生活图片,运用投影仪播放,让学生对三角形有一个感性认识.
二、讲授新知:
三角形的定义
由不在同一直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形
如图:点A、 B、 C叫做 三角形的 __________ A
线段AB、AC、BC叫做三角形的 __________ .
∠ A、 ∠ B、 ∠ C叫做三角形的_________
c b
三角形的边:线段AB、AC、BC分别表示为c、b、a
B a C
三角形用符号 “Δ”表示,如图顶点是A、B、C的三角形,记作“ΔABC”读作“三角形ABC”
三角形按边的关系分类
不等边三角形 等腰三角形 等边三角形
(三边互不相等) (有两边相等) (三边都相等)
不等边三角形
等腰三角形(等边三角形是等腰三角形的特例,又叫正三角形)
等腰三角形各部分的名称
注意:腰、底边、顶角、底角等是相对于等腰三角形来说的,一般的三角形则不存在这些概念。
动动手
任意两边之和与第三边的大小 关系用不等式表示为:
思考:三角形的三边有怎样的关系?
猜想:三角形任何两边的和大于第三边!
理论验证:“两点之间的所有连线中,线段最短” AC+CB>AB
同理可得:AB+BC>AC, AB+AC>BC
三角形的三边关系:
1、 三角形中任何两边的和大于第三边
2、 三角形中任何两边的差小于第三边
对应练习:
下列长度的三条线段能否组成三角形?为什么?
(1) 2cm,3cm,4cm ( ) (2) 1cm,3cm,4cm ( )
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
解题技巧:只要比较两条较短线段之和与最长线段的大小
例题讲解:
例1:等腰三角形中,周长为18cm,
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长。
解:(1)设等腰三角形的底边长为xcm,根据题意,得
x+2x+2x=18
解方程,得
x=3.6
所以三角形的三边长为3.6cm,7.2cm,7.2cm
(2)若底边长为4cm,设腰长为xcm。根据题意,得
2x+4=18 解方程,得 x=7
若腰长为4cm,设底边长为xcm。根据题意,得
2×4+x=18 解方程,得 x=10
由于4+4<10,可知以4cm为腰长不能构成周长为18cm的等腰三角形。
所以,三角形的另两边长都是7cm
练习:
1.图中有几个三角形?分别是那几个?
2.若一个三角形三边长度之比为2:3:3,周长为16cm,则三角形的三边长分别是 , 这个三角形若按边分类是 .三角形
3.三角形中,已知两边长4cm和8cm,另一边长与前面的其中一边长相等,这个三角形的周长是 cm
三课堂小结
三角形
B
B
