钉子板上的多边形 课件(共20张PPT)
图片预览

文档简介
(共20张PPT)
B
D
A
C
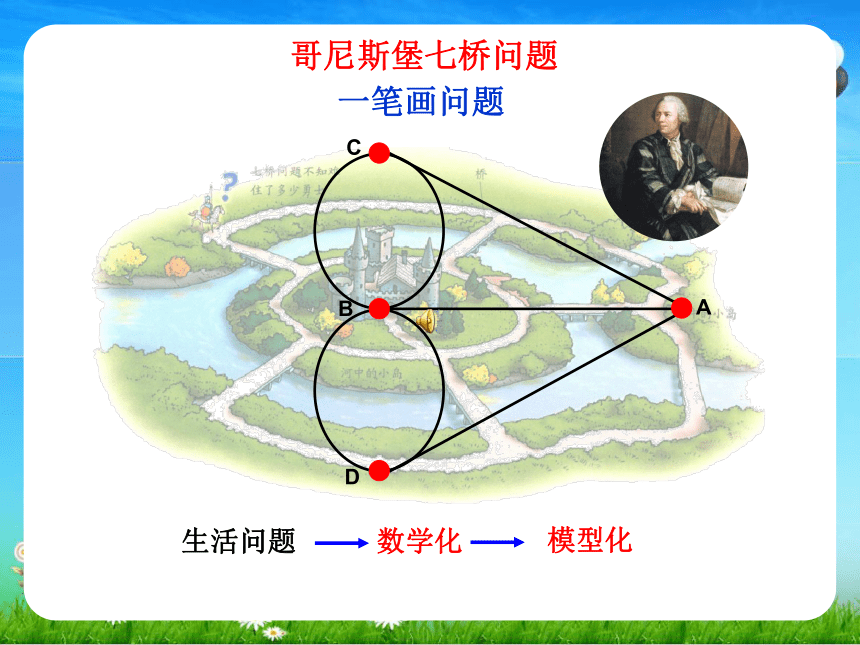
生活问题
数学化
模型化
哥尼斯堡七桥问题
一笔画问题
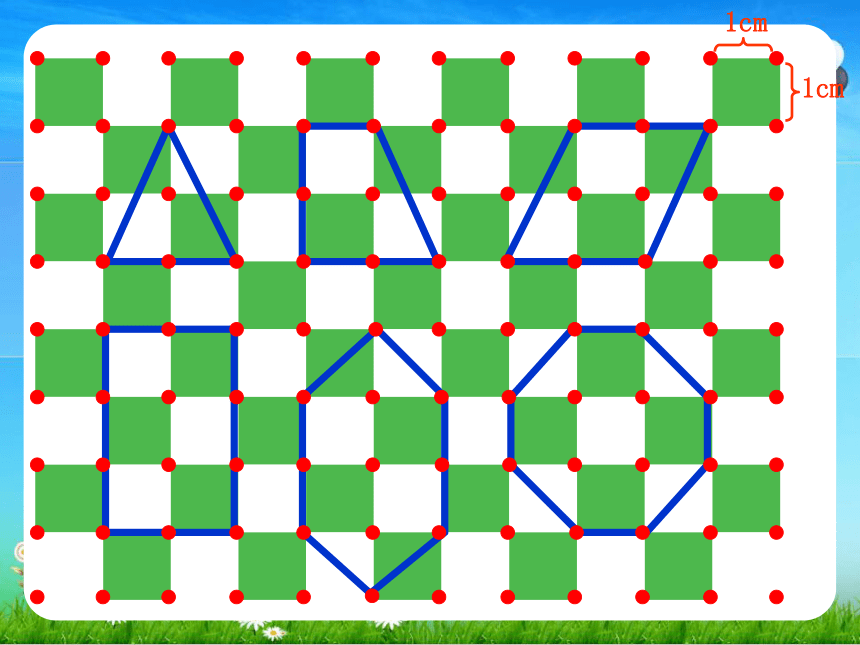
1cm
1cm
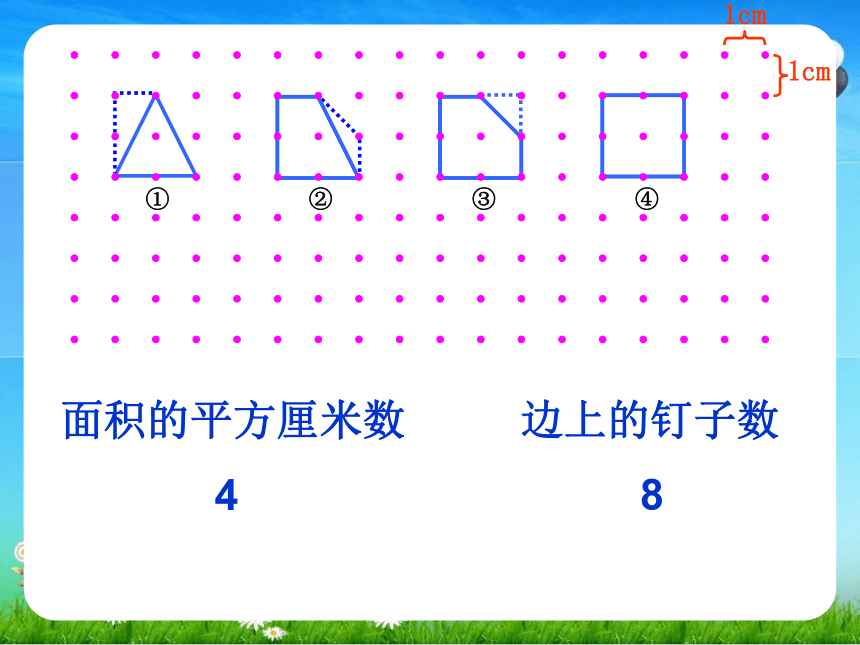
边上的钉子数
面积的平方厘米数
8
4
① ② ③ ④
1cm
1cm
① ② ③ ④
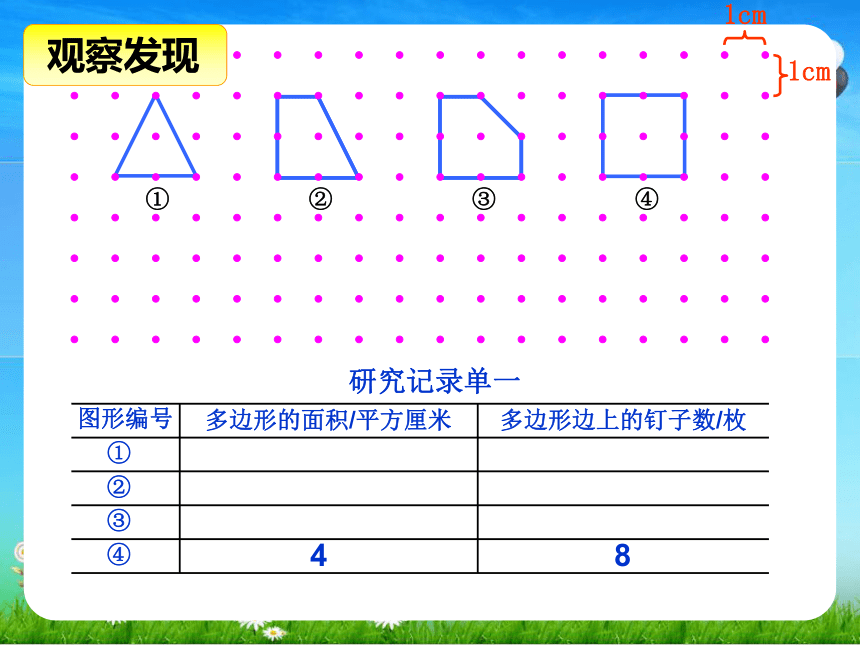
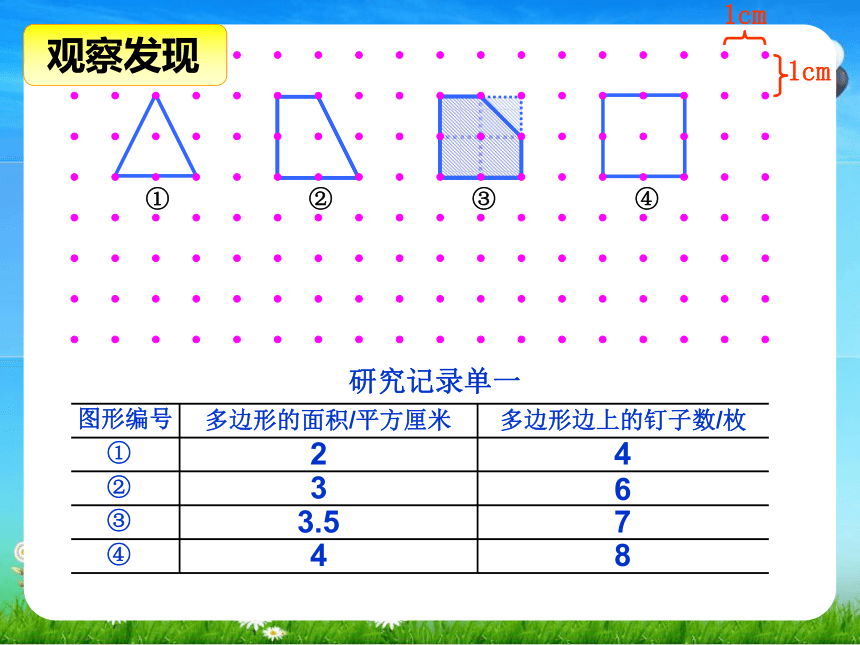
研究记录单一
图形编号
多边形的面积/平方厘米
多边形边上的钉子数/枚
①
②
③
④
观察发现
8
4
1cm
1cm
图形编号
多边形的面积/平方厘米
2
3
3.5
4
6
① ② ③ ④
研究记录单一
观察发现
8
4
7
①
②
③
④
1cm
1cm
多边形边上的钉子数/枚
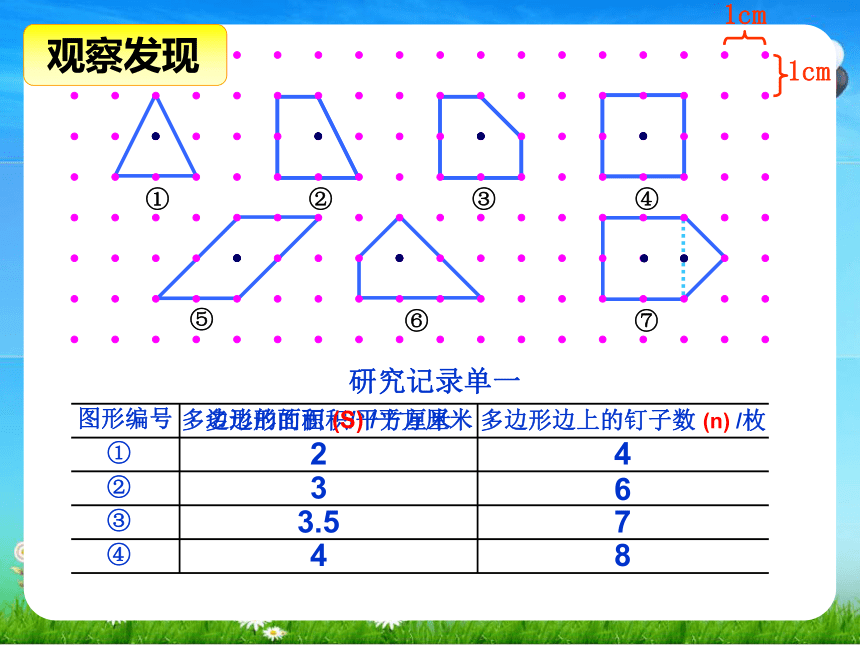
图形编号
多边形的面积/平方厘米
多边形边上的钉子数 (n) /枚
2
3
3.5
4
6
① ② ③ ④
多边形的面积 (S) /平方厘米
7
8
4
⑤
⑥
⑦
观察发现
研究记录单一
①
②
③
④
1cm
1cm
① ② ③ ④
⑤
⑥
观察发现
图形编号
2
3
3.5
4
6
7
8
4
研究记录单一
研究报告一
S=
当多边形内有 枚钉子时,
多边形的面积 (S) /平方厘米
多边形边上的钉子数 (n) /枚
①
②
③
④
1cm
1cm
n÷2
1
1cm
1cm
①
1cm
1cm
①
探索发现
1cm
1cm
(1)每组在钉子板上再围1个内部钉子数是2的多边形作为②号图形。
(2)把边上的钉子数和面积数填写在研究记录单二中。
(3)说说你有什么发现。
研究记录单二
图形编号
多边形边上的钉子数(n)/枚
多边形的面积(S)/平方厘米
①
8
5
②
研究记录单二
图形编号
多边形边上的钉子数(n)/枚
多边形的面积(S)/平方厘米
①
8
5
②
③
④
当多边形内有2枚钉子时,S=n÷2+1。
①
探索发现
1cm
1cm
研究报告二
举例验证
(2)依次找出它的面积数和边上钉子数。
(3)验证是否符合我们的猜想。
(1)每组围出1个内部钉子数是3的多边形。
研究记录单三
当多边形内有 枚钉子时,S=
猜想验证
(1)你们组准备研究内部钉子数是几的多边形呢?请协商确定。
(2)猜想有什么规律呢?请写出来。
(3)围出相应的图形并收集相关数据进行验证,完成研究记录单三。
1 S = n ÷ 2
2 S = n ÷ 2 + 1
3 S = n ÷ 2 + 2
……
S = n ÷ 2 +
……
S = n ÷ 2 +
S = n ÷ 2
18
a
(a – 1)
0
– 1
19
1 S = n ÷ 2
2 S = n ÷ 2 + 1
3 S = n ÷ 2 + 2
……
……
S = n ÷ 2
0
– 1
S = n ÷ 2 +
a
(a – 1)
18
S = n ÷ 2 +
19
S=n÷2+ (a – 1)
钉子板上的多边形面积与钉子数之间的关系
终 结 报 告
S——多边形的面积
a——内部钉子数
n——边上钉子数
奥地利数学家乔治·皮克
在1899年发现, 钉子板上的多边形,其面积S与内部钉子数a、边上钉子数n有以下关系:
S=n÷2+(a-1)。
B
D
A
C
生活问题
数学化
模型化
哥尼斯堡七桥问题
一笔画问题
1cm
1cm
边上的钉子数
面积的平方厘米数
8
4
① ② ③ ④
1cm
1cm
① ② ③ ④
研究记录单一
图形编号
多边形的面积/平方厘米
多边形边上的钉子数/枚
①
②
③
④
观察发现
8
4
1cm
1cm
图形编号
多边形的面积/平方厘米
2
3
3.5
4
6
① ② ③ ④
研究记录单一
观察发现
8
4
7
①
②
③
④
1cm
1cm
多边形边上的钉子数/枚
图形编号
多边形的面积/平方厘米
多边形边上的钉子数 (n) /枚
2
3
3.5
4
6
① ② ③ ④
多边形的面积 (S) /平方厘米
7
8
4
⑤
⑥
⑦
观察发现
研究记录单一
①
②
③
④
1cm
1cm
① ② ③ ④
⑤
⑥
观察发现
图形编号
2
3
3.5
4
6
7
8
4
研究记录单一
研究报告一
S=
当多边形内有 枚钉子时,
多边形的面积 (S) /平方厘米
多边形边上的钉子数 (n) /枚
①
②
③
④
1cm
1cm
n÷2
1
1cm
1cm
①
1cm
1cm
①
探索发现
1cm
1cm
(1)每组在钉子板上再围1个内部钉子数是2的多边形作为②号图形。
(2)把边上的钉子数和面积数填写在研究记录单二中。
(3)说说你有什么发现。
研究记录单二
图形编号
多边形边上的钉子数(n)/枚
多边形的面积(S)/平方厘米
①
8
5
②
研究记录单二
图形编号
多边形边上的钉子数(n)/枚
多边形的面积(S)/平方厘米
①
8
5
②
③
④
当多边形内有2枚钉子时,S=n÷2+1。
①
探索发现
1cm
1cm
研究报告二
举例验证
(2)依次找出它的面积数和边上钉子数。
(3)验证是否符合我们的猜想。
(1)每组围出1个内部钉子数是3的多边形。
研究记录单三
当多边形内有 枚钉子时,S=
猜想验证
(1)你们组准备研究内部钉子数是几的多边形呢?请协商确定。
(2)猜想有什么规律呢?请写出来。
(3)围出相应的图形并收集相关数据进行验证,完成研究记录单三。
1 S = n ÷ 2
2 S = n ÷ 2 + 1
3 S = n ÷ 2 + 2
……
S = n ÷ 2 +
……
S = n ÷ 2 +
S = n ÷ 2
18
a
(a – 1)
0
– 1
19
1 S = n ÷ 2
2 S = n ÷ 2 + 1
3 S = n ÷ 2 + 2
……
……
S = n ÷ 2
0
– 1
S = n ÷ 2 +
a
(a – 1)
18
S = n ÷ 2 +
19
S=n÷2+ (a – 1)
钉子板上的多边形面积与钉子数之间的关系
终 结 报 告
S——多边形的面积
a——内部钉子数
n——边上钉子数
奥地利数学家乔治·皮克
在1899年发现, 钉子板上的多边形,其面积S与内部钉子数a、边上钉子数n有以下关系:
S=n÷2+(a-1)。
