2022-2023学年人教版数学七年级上册(重庆地区)第四章 几何图形初步 期末复习题 (含解析)
文档属性
| 名称 | 2022-2023学年人教版数学七年级上册(重庆地区)第四章 几何图形初步 期末复习题 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 875.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 09:13:52 | ||
图片预览




文档简介
第四章 几何图形初步 期末复习题
一、单选题
1.(2022·重庆市育才中学七年级期末)如图,将一个直角三角形绕它的一条直角边所在的直线旋转一周,得到的几何体是圆锥,这一现象能用以下哪个数学知识解释( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交得线
2.(2022·重庆九龙坡·七年级期末)下列是正方体展开图的是( )
A. B.
C. D.
3.(2022·重庆·西南大学附中七年级期末)如图是一个正方体的展开图,将它折叠成正方体后,有“喜”字一面的对面上的字是( )
A.我 B.欢 C.数 D.学
4.(2022·重庆·西南大学附中七年级期末)如图,点为线段的中点,点为的中点,若,,则线段的长( )
A.7 B. C.6 D.5
5.(2022·重庆一中七年级期末)下列说法正确的是( )
A.经过两点有且只有一条直线
B.两点之间的距离就是连接两点的线段
C.如果,那么点是线段的中点
D.两点之间直线最短
6.(2022·重庆南开中学七年级期末)下列语句正确的是( ).
A.延长射线AB B.线段MN叫做点M,N间的距离
C.两点之间,直线最短 D.直线a,b相交于点P
7.(2022·重庆长寿·七年级期末)利用一副三角板上已知度数的角,不能画出的角是( )
A.15° B.100° C.165° D.135°
8.(2022·重庆市潼南中学校七年级期末)如图,下列说法中错误的是( )
A.OA的方向是东北方向 B.OB的方向是北偏西60°
C.OC的方向是南偏西60° D.OD的方向是南偏东60°
9.(2022·重庆綦江·七年级期末)如图,与互余,平分,则的度数是( )
A. B. C. D.
10.(2022·重庆南川·七年级期末)在9:30这一时刻,时钟上的时针和分针之间的夹角为( )
A. B. C. D.
二、填空题
11.(2022·重庆九龙坡·七年级期末)150°角的补角为________度.
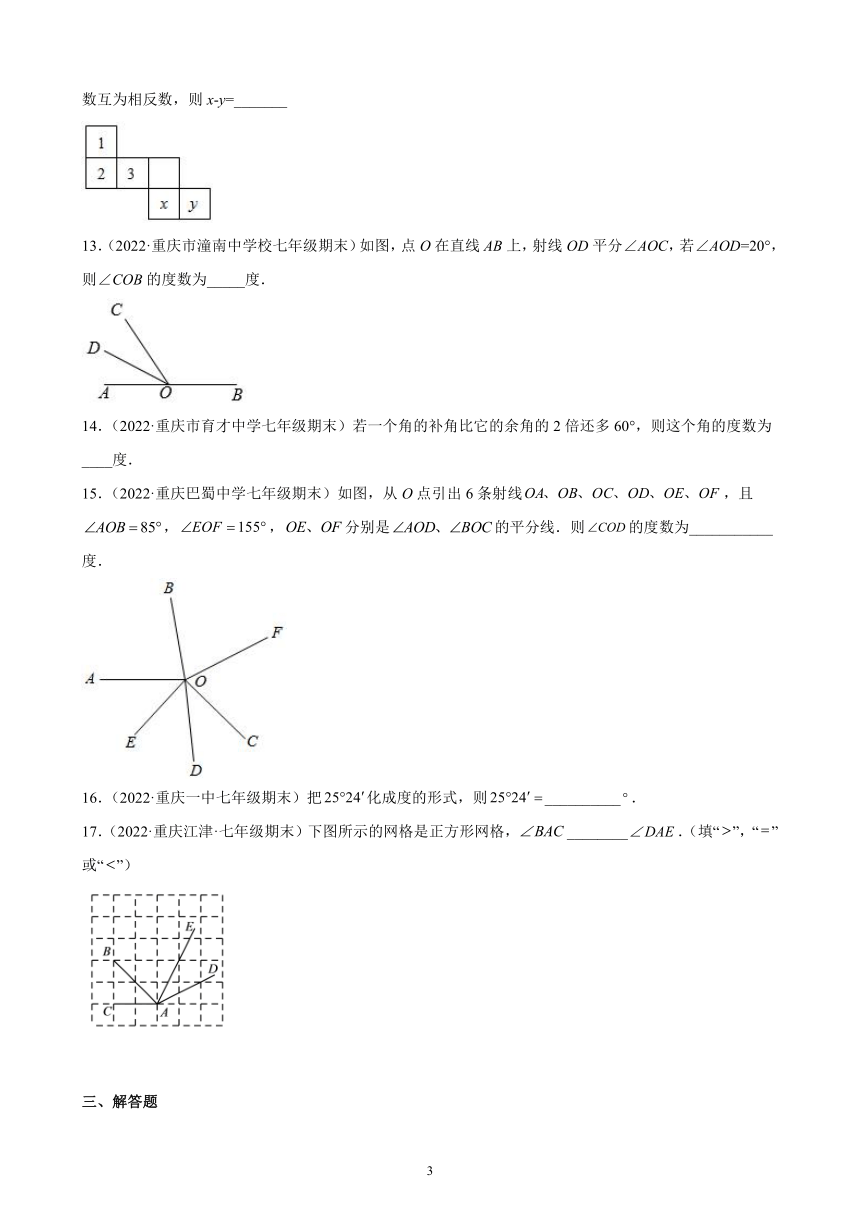
12.(2022·重庆巴蜀中学七年级期末)如下图,若要使图中的平面展开图折叠成正方体后,相对面上两个数互为相反数,则x-y=_______
13.(2022·重庆市潼南中学校七年级期末)如图,点O在直线AB上,射线OD平分∠AOC,若∠AOD=20°,则∠COB的度数为_____度.
14.(2022·重庆市育才中学七年级期末)若一个角的补角比它的余角的2倍还多60°,则这个角的度数为____度.
15.(2022·重庆巴蜀中学七年级期末)如图,从O点引出6条射线,且,,分别是的平分线.则的度数为___________度.
16.(2022·重庆一中七年级期末)把化成度的形式,则__________.
17.(2022·重庆江津·七年级期末)下图所示的网格是正方形网格,________.(填“”,“”或“”)
三、解答题
18.(2022·重庆长寿·七年级期末)计算下列各题:
(1);
(2).
19.(2022·重庆一中七年级期末)如图,已知线段,,求作:一条线段(保留作图痕迹,不要求写作法).
20.(2022·重庆巴蜀中学七年级期末)如图,已知线段AD上从左到右依次有B、C两点,若AD=30,AB:BC:CD=3:1:2,点M是AC的中点.N是线段CD的中点,求线段MN的长.
21.(2022·重庆南开中学七年级期末)如图,在同一平面内有三个点A、B、C.
(1)连接AC,面出直线AB,射线BC;
(2)尺规作图(保留作图痕迹):在线段AC上作一点D,使得.
22.(2022·重庆彭水·七年级期末)如图,点O在直线AB上,OC平分,.
(1)已知,求的大小;
(2)若,请判断OE是否平分,并说明理由.
23.(2022·重庆·巴川初级中学校七年级期末)如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
24.(2022·重庆一中七年级期末)如图,是内部的一条射线,是内部的一条射线,是内部的一条射线.
(1)如图1,、分别是、的角平分线,已知,,求的度数;
(2)如图2,若,,且,求的度数.
25.(2022·重庆市璧山区正兴初级中学校七年级期末)如图,已知,是内的一条射线,且.
(1)求,的度数;
(2)作射线平分,在内作射线,使得,求的度数;
(3)过点作射线,若,求的度数.
26.(2022·重庆市潼南中学校七年级期末)如图1,点为直线上一点,过点作射线,使,将直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)在图1中,_______,_______;
(2)将图1中的三角板按图2的位置放置,使得在射线上,求的度数
(3)将上述直角三角板按图3的位置放置,使得在的内部,求的度数.
27.(2022·重庆八中七年级期末)一副三角板按如图1所示放置,边在直线上,.
(1)求图1中的度数;
(2)如图2,将三角板绕点O顺时针旋转,转速为,同时将三角板绕点O逆时针旋转,转速为,当旋转到射线上时,两三角板都停止转动.设转动时间为.
①在范围内,当时,求t的值;
②如图3,旋转过程中,作的角平分线,当时.直接写出时间的值.
28.(2022·重庆市育才中学七年级期末)已知∠AOD=130°,∠BOC=50°,OM平分∠AOC,ON平分∠BOD.
(1)如图1,若,求∠NOC的度数;
(2)将∠BOC顺时针旋转至如图2的位置,求∠MON的度数.
参考答案:
1.C
【分析】根据一个直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥即可解答.
【详解】解:∵一个直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥
∴体现了面动成体.
故选:C.
【点睛】本题主要考查了点线面体的关系,掌握点线面体的关系成为解答本题的关键.
2.B
【分析】根据平面图形的折叠及正方体的展开图解题得出即可.
【详解】解:根据正方体的展开图,A、C、D折在一起会有重叠的情况,对折不能折成正方体;
B折在一起可以构成正方体,
故选B
【点睛】此题考查几何体的展开图,解题关键在于掌握正方体展开图的各种情形.
3.C
【分析】根据正方体的表面展开图的特征即可判断.
【详解】解:由正方体的表面展开图的特征可知:
“喜”的对面是“数”.
故选:C.
【点睛】本题考查了正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确解题的关键.
4.C
【分析】应用一条线上的线段和差关系进行计算即可得出答案.
【详解】解:∵点D为线段AB的中点,
∴AD=BD=AB=×16=8,
∵AD=AE+DE,DE=AE,
∴AE+AE=8,
∴AE=6,DE=2,
∵点C为DB的中点,
∴CD=BD=×8=4,
∴CE=DE+CD=2+4=6,
故选:C.
【点睛】本题主要考查了一条线上各个线段关系,看清图中线段关系,熟练掌握两点间的距离计算方法进行求解是解决本题的关键.
5.A
【分析】根据直线的性质,线段的中点,两点之间的距离逐项分析即可.
【详解】A.经过两点有且只有一条直线,正确;
B.两点之间的距离就是连接两点的线段的长度,故不正确;
C.如果,那么点可能是线段的中点,点P也可能在线段AB外,故不正确;
D.两点之间线段最短,故不正确;
故选A.
【点睛】本题考查了直线的性质,线段的中点,两点之间的距离,熟练掌握线段上的点把线段分成相等的两条线段,那么这个点是这条线段的中点是解答本题的关键.
6.D
【分析】根据线段的定义、以及射线的延伸性即可作出判断.
【详解】解:、射线是无限延伸的,故选项错误,不符合题意;
、线段的长度叫做它们间的距离,故选项错误,不符合题意;
、两点之间,线段最短,故选项错误,不符合题意;
、直线a,b相交于点P,说法正确,符合题意.
故选:D.
【点睛】本题考查了线段和射线的定义,解题的关键是理解射线的延伸性.
7.B
【分析】用三角板画出角,用角度加减法,根据选项一一分析,排除错误答案.
【详解】解:A. 的角,.
B.画不出 的角,
C. 的角,.
D. 的角,.
故选B.
【点睛】用三角板直接画特殊角的步骤:先画一条射线,再把三角板所画角的一边与射线重合,顶点与射线端点重合,最后沿另一边画一条射线,标出角的度数.
8.D
【分析】准确地找到对应的角度,关键是射线和南北方向之间的夹角,一一求出角度即可判断正误.
【详解】解:A、的方向是北偏东45度即东北方向,故正确,不符合题意;
B、的方向是北偏西,故正确,不符合题意;
C、的方向是南偏西,故正确,不符合题意;
D、的方向是南偏东,故错误,符合题意.
故选:D.
【点睛】本题主要考查了方位角的运用,解题的关键是会准确地找到所对应的角度是需要掌握的基本能力之一.
9.B
【分析】先根据余角的定义,求出∠AOC的度数,再根据角平分线的定义∠DOC的度数,即可求得∠BOD的度数.
【详解】解:∵∠AOC与∠COB互余,∠COB=15°,
∴∠AOC=90°﹣∠BOC=90°﹣15°=75°,
∵OC平分∠AOD,
∴∠DOC=∠AOC=75°,
∴∠BOD=∠DOC﹣∠BOC=75°﹣15°=60°,
故选:B.
【点睛】本题考查余角定义、角平分线的定义,熟知余角的定义是解答的关键.
10.A
【分析】根据时针与分针相距的份数乘以每份的度数,可得答案.
【详解】解:9:30时针与分针相距3.5份,每份的度数是30°,
在时刻9:30,时钟上时针和分针之间的夹角(小于平角的角)为3.5×30°=105°.
故选:A.
【点睛】本题考查了钟面角,利用时针与分针相距的份数乘以每份的度数是解题关键.
11.30
【详解】解:∵180°-150°=30°,
∴150°角的补角为30°.
故答案为:30.
【点睛】本题考查的是余角和补角的定义,如果两个角的和是一个直角,那么称这两个角互为余角.如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角.
12.2
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“1”与“x”是相对面,
“3”与“y”是相对面,
∵相对面上两个数互为相反数,
∴x=-1,y=-3,
∴x-y=(-1)-(-3)=-1+3=2.
故答案为:2.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
13.140
【详解】解:∵OD平分∠AOC,
∴∠AOC=2∠AOD=40°,
∴∠COB=180°﹣∠COA=140°
故答案为:140
14.60
【分析】设出所求的角为x,则它的补角为180°-x,余角为90°-x,根据题意列出方程,再解方程即可求解.
【详解】解:设这个角的度数是x,则它的补角为:180°-x,余角为90°-x;
由题意,得:(180°-x)-2(90°-x)=60°.
解得:x=60°.
答:这个角的度数是60°.
故答案为:60.
【点睛】本题考查了余角和补角的定义;根据角之间的互余和互补关系列出方程是解决问题的关键.
15.35
【分析】根据分别是的平分线.得出∠AOE=∠DOE,∠BOF=∠COF,可得∠AOE+∠BOF=∠DOE+∠COF=∠EOF-∠COD=155°-∠COD,根据周角∠AOB+∠AOE+∠BOF+∠EOF=360°,得出85°+155°-∠COD+155°=360°,解方程即可.
【详解】解:∵分别是的平分线.
∴∠AOE=∠DOE,∠BOF=∠COF,
∴∠AOE+∠BOF=∠DOE+∠COF=∠EOF-∠COD=155°-∠COD,
∵∠AOB+∠AOE+∠BOF+∠EOF=360°,
∴85°+155°-∠COD+155°=360°,
解得∠COD=35°.
故答案为35.
【点睛】本题考查角平分线有关的计算,角的和差,周角性质,一元一次方程,掌握角平分线有关的计算,角的和差,周角性质,一元一次方程是解题关键.
16..
【分析】根据角度的单位换算1°=60′,求出24′÷60′=0.4°即可.
【详解】解:∵1°=60′,
∴24÷60°=0.4°,
∴.
故答案为:.
【点睛】本题考查角度单位换算,掌握角的由大单位变小单位用乘法,由小单位变大单位用除法是解题关键.
17.>
【分析】构造等腰直角三角形,根据等腰直角三角形的性质即可进行比较大小.
【详解】解:如下图所示,
是等腰直角三角形,
∴,
∴.
故答案为
另:此题也可直接测量得到结果.
【点睛】本题考查等腰直角三角形的性质,构造等腰直角三角形是解题的关键.
18.(1)
(2)
【分析】(1)按照运算顺序,先算乘方,再算乘法,最后算加减,然后进行计算即可;
(2)根据度分秒的进制进行计算即可.
(1)
解:原式
.
(2)
解:原式
.
【点睛】本题考查了度分秒的换算,有理数的混合运算,准确熟练地进行计算是解题的关键.
19.见解析
【分析】在射线AP上依次截取AE=EF=a,在EF上截取FB=b,则线段AB满足条件.
【详解】解:如图,AB为所作;
【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
20.线段MN的长为15.
【分析】根据线段中点的定义和线段的和差倍分关系即可得到结论
【详解】解:∵AB:BC:CD=3:1:2,且AD=30,
∴AB=15,BC=5,AB=10,
∴AC= AB+BC=20,
∵点M是AC的中点,N是线段CD的中点,
∴MC=AC=10,CN=CD=5,
∴MN=MC+CN=15.
∴线段MN的长为15.
【点睛】本题考查了线段的中点和求两点之间的距离,能求出各个线段的长度是解此题的关键.
21.(1)见解析
(2)见解析
【分析】(1)根据题意作出线段,直线,射线即可;
(2)在线段上截取,点即为所求.
(1)
连接AC,面出直线AB,射线BC;如图所示,
(2)
如图,在线段上截取,点即为所求,
【点睛】本题考查了尺规作图-作线段等于已知线段,画线段、射线、直线,掌握线段、射线、直线的特点是解题的关键.
22.(1)
(2)OE平分,理由见解析
【分析】(1)根据,OC平分,可知;根据,可知,以此即可求出的度数;
(2)按照(1)求值的思路,将数字换为字母进行证明即可.
(1)
解OC平分,,
,
,
,
又,
;
(2)
OE平分,理由如下:
平分,,
,
又,
;
平分.
【点睛】本题主要考查的是角度的计算,角平分线的应用,熟练掌握角度之间的运算是解题的关键.
23.(1)BF∥DE,理由见解析;(2)60°
【分析】(1)由于∠AGF=∠ABC,可判断GF∥BC,则∠1=∠3,由∠1+∠2=180°,得出∠3+∠2=180°判断出BF∥DE;
(2)由∠2=150°得出∠1=30°,再根据垂直定义进而得出∠AFG的度数.
【详解】解:(1)BF∥DE.理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE;
(2)∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∵BF⊥AC
∴∠BFA=90°
∴∠AFG=90°﹣30°=60°.
【点睛】本题考查了平行线的判定与性质,解题的关键是掌握同位角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,内错角相等.
24.(1)110°
(2)100°
【分析】(1)由OM是∠AOB的角平分线,∠AOB=30°,得到,则∠BON=∠MON-∠BOM=55°,再由ON是∠BOC的角平分线,得到∠BOC=2∠BON=110°;
(2)设∠AOM=∠NOC=x,则∠AOB=4x,可推出∠BOM=3x,∠BOM:∠BON=3:2,得到∠BON=2x,根据∠AOC=∠AOB+∠BON+∠NOC=7x=140°,得到x=20°,则∠MON=∠BOM+∠BON=5x=100°.
(1)
解:∵OM是∠AOB的角平分线,∠AOB=30°,
∴,
∵∠MON=70°,
∴∠BON=∠MON-∠BOM=55°,
∵ON是∠BOC的角平分线,
∴∠BOC=2∠BON=110°;
(2)
解:设∠AOM=∠NOC=x,则∠AOB=4x,
∴∠BOM=∠AOB-∠AOM=3x,
∵∠BOM:∠BON=3:2,
∴∠BON=2x,
∴∠AOC=∠AOB+∠BON+∠NOC=7x=140°,
∴x=20°,
∴∠MON=∠BOM+∠BON=5x=100°.
【点睛】本题主要考查了几何中角度的计算,角平分线的定义,解题的关键在于能够熟练掌握相关知识.
25.(1),;(2);(3)50°或140°.
【分析】(1)根据,即可求解;
(2)先求出∠COM,再求出∠CON,相加即可求解;
(3)分当OD在内部和外部两种情况分类讨论即可求解.
【详解】解:(1)∵,
∴,
;
(2)∵平分,
∴,
∵ ,
∴,
∴ ;
(3)如图1,当OD在内部时,
∵,
∴∠BOD=,
∴∠COD=∠BOC-∠BOD=80°-30°=50°;
如图2,当OD在外部时,
∵,
∴∠BOD=,
∴∠COD=∠BOC+∠BOD=80°+60°=140°,
∴的度数为50°或140°.
.
【点睛】本题考查了角的计算,熟知角的特点和比例意义并根据题意画图求解是解题关键.
26.(1)120°,60°;(2)30°;(3)30°.
【分析】(1)点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,可以求得∠AOC和∠BOC的度数;
(2)根据∠AOC的度数和∠MON的度数可以得到∠CON的度数;
(3)根据∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,可以得到∠BON-∠COM的度数.
【详解】解:(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
【点睛】本题考查了角的计算,解题的关键是找出各个角之间的关系,与已知条件建立关系,然后求出所求角的度数.
27.(1)
(2)①2s;②s或s或s.
【分析】(1)利用角的和差关系可得从而可得答案;
(2)①先求解重合的时间,再画出图形,结合几何图形与角的和差关系列方程,再解方程即可;②分情况讨论:当时,结合①可得 当时, 当时,利用角的和差关系列方程 解方程即可,当时,如图,当 利用角的和差关系列方程 再解方程即可,当时, 当时,利用角的和差关系列方程,再解方程即可,从而可得答案.
【详解】(1)解: ,
(2)解:① 则重合时的时间为:(s),
当时,
解得:
所以当旋转2s时,
②当旋转到射线上时,(s),
当时,结合①可得
当重合时,(s),重合时,(s),如图,
所以当时,
当重合时,(s),如图,
当时,
平分
解得:
当重合时,(s),
当时,如图,
平分
解得: 不符合题意,舍去,
当重合时,(s),
当
平分
解得:
如图,当再次重合时,(s),
当时,
如图,当重合时,(s)
当时,
平分
解得:
综上:当时,s或s或s.
【点睛】本题考查的是几何图形中角的和差关系,角的动态定义的理解,一元一次方程的应用,“数形结合与利用一元一次方程解决动态几何问题”是解本题的关键.
28.(1)4°
(2)40°
【分析】(1)设 利用角平分线的定义可求得∠AOM=,∠DON,再根据列式求出,求出,再减去的度数,结论可得;
(2)根据角平分线的定义可求得∠AOM,∠BON,再利用角的和差得出结论.
(1)
设
∵
∴
∵是的平分线
∴;
∵
∴
∵是的平分线,
∴
∵
∴
解得,
∴
∴
∴
∵
∴
(2)
由图可得,
∵是的平分线
∴
又
∵是的平分线,
∴
∴
∵∠AOD=130°,∠BOC=50°,
∴
【点睛】本题主要考查了角的计算,角平分线的定义.本题是探究型题目,利用类比的方法解答是解题的关键.
一、单选题
1.(2022·重庆市育才中学七年级期末)如图,将一个直角三角形绕它的一条直角边所在的直线旋转一周,得到的几何体是圆锥,这一现象能用以下哪个数学知识解释( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交得线
2.(2022·重庆九龙坡·七年级期末)下列是正方体展开图的是( )
A. B.
C. D.
3.(2022·重庆·西南大学附中七年级期末)如图是一个正方体的展开图,将它折叠成正方体后,有“喜”字一面的对面上的字是( )
A.我 B.欢 C.数 D.学
4.(2022·重庆·西南大学附中七年级期末)如图,点为线段的中点,点为的中点,若,,则线段的长( )
A.7 B. C.6 D.5
5.(2022·重庆一中七年级期末)下列说法正确的是( )
A.经过两点有且只有一条直线
B.两点之间的距离就是连接两点的线段
C.如果,那么点是线段的中点
D.两点之间直线最短
6.(2022·重庆南开中学七年级期末)下列语句正确的是( ).
A.延长射线AB B.线段MN叫做点M,N间的距离
C.两点之间,直线最短 D.直线a,b相交于点P
7.(2022·重庆长寿·七年级期末)利用一副三角板上已知度数的角,不能画出的角是( )
A.15° B.100° C.165° D.135°
8.(2022·重庆市潼南中学校七年级期末)如图,下列说法中错误的是( )
A.OA的方向是东北方向 B.OB的方向是北偏西60°
C.OC的方向是南偏西60° D.OD的方向是南偏东60°
9.(2022·重庆綦江·七年级期末)如图,与互余,平分,则的度数是( )
A. B. C. D.
10.(2022·重庆南川·七年级期末)在9:30这一时刻,时钟上的时针和分针之间的夹角为( )
A. B. C. D.
二、填空题
11.(2022·重庆九龙坡·七年级期末)150°角的补角为________度.
12.(2022·重庆巴蜀中学七年级期末)如下图,若要使图中的平面展开图折叠成正方体后,相对面上两个数互为相反数,则x-y=_______
13.(2022·重庆市潼南中学校七年级期末)如图,点O在直线AB上,射线OD平分∠AOC,若∠AOD=20°,则∠COB的度数为_____度.
14.(2022·重庆市育才中学七年级期末)若一个角的补角比它的余角的2倍还多60°,则这个角的度数为____度.
15.(2022·重庆巴蜀中学七年级期末)如图,从O点引出6条射线,且,,分别是的平分线.则的度数为___________度.
16.(2022·重庆一中七年级期末)把化成度的形式,则__________.
17.(2022·重庆江津·七年级期末)下图所示的网格是正方形网格,________.(填“”,“”或“”)
三、解答题
18.(2022·重庆长寿·七年级期末)计算下列各题:
(1);
(2).
19.(2022·重庆一中七年级期末)如图,已知线段,,求作:一条线段(保留作图痕迹,不要求写作法).
20.(2022·重庆巴蜀中学七年级期末)如图,已知线段AD上从左到右依次有B、C两点,若AD=30,AB:BC:CD=3:1:2,点M是AC的中点.N是线段CD的中点,求线段MN的长.
21.(2022·重庆南开中学七年级期末)如图,在同一平面内有三个点A、B、C.
(1)连接AC,面出直线AB,射线BC;
(2)尺规作图(保留作图痕迹):在线段AC上作一点D,使得.
22.(2022·重庆彭水·七年级期末)如图,点O在直线AB上,OC平分,.
(1)已知,求的大小;
(2)若,请判断OE是否平分,并说明理由.
23.(2022·重庆·巴川初级中学校七年级期末)如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
24.(2022·重庆一中七年级期末)如图,是内部的一条射线,是内部的一条射线,是内部的一条射线.
(1)如图1,、分别是、的角平分线,已知,,求的度数;
(2)如图2,若,,且,求的度数.
25.(2022·重庆市璧山区正兴初级中学校七年级期末)如图,已知,是内的一条射线,且.
(1)求,的度数;
(2)作射线平分,在内作射线,使得,求的度数;
(3)过点作射线,若,求的度数.
26.(2022·重庆市潼南中学校七年级期末)如图1,点为直线上一点,过点作射线,使,将直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)在图1中,_______,_______;
(2)将图1中的三角板按图2的位置放置,使得在射线上,求的度数
(3)将上述直角三角板按图3的位置放置,使得在的内部,求的度数.
27.(2022·重庆八中七年级期末)一副三角板按如图1所示放置,边在直线上,.
(1)求图1中的度数;
(2)如图2,将三角板绕点O顺时针旋转,转速为,同时将三角板绕点O逆时针旋转,转速为,当旋转到射线上时,两三角板都停止转动.设转动时间为.
①在范围内,当时,求t的值;
②如图3,旋转过程中,作的角平分线,当时.直接写出时间的值.
28.(2022·重庆市育才中学七年级期末)已知∠AOD=130°,∠BOC=50°,OM平分∠AOC,ON平分∠BOD.
(1)如图1,若,求∠NOC的度数;
(2)将∠BOC顺时针旋转至如图2的位置,求∠MON的度数.
参考答案:
1.C
【分析】根据一个直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥即可解答.
【详解】解:∵一个直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥
∴体现了面动成体.
故选:C.
【点睛】本题主要考查了点线面体的关系,掌握点线面体的关系成为解答本题的关键.
2.B
【分析】根据平面图形的折叠及正方体的展开图解题得出即可.
【详解】解:根据正方体的展开图,A、C、D折在一起会有重叠的情况,对折不能折成正方体;
B折在一起可以构成正方体,
故选B
【点睛】此题考查几何体的展开图,解题关键在于掌握正方体展开图的各种情形.
3.C
【分析】根据正方体的表面展开图的特征即可判断.
【详解】解:由正方体的表面展开图的特征可知:
“喜”的对面是“数”.
故选:C.
【点睛】本题考查了正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确解题的关键.
4.C
【分析】应用一条线上的线段和差关系进行计算即可得出答案.
【详解】解:∵点D为线段AB的中点,
∴AD=BD=AB=×16=8,
∵AD=AE+DE,DE=AE,
∴AE+AE=8,
∴AE=6,DE=2,
∵点C为DB的中点,
∴CD=BD=×8=4,
∴CE=DE+CD=2+4=6,
故选:C.
【点睛】本题主要考查了一条线上各个线段关系,看清图中线段关系,熟练掌握两点间的距离计算方法进行求解是解决本题的关键.
5.A
【分析】根据直线的性质,线段的中点,两点之间的距离逐项分析即可.
【详解】A.经过两点有且只有一条直线,正确;
B.两点之间的距离就是连接两点的线段的长度,故不正确;
C.如果,那么点可能是线段的中点,点P也可能在线段AB外,故不正确;
D.两点之间线段最短,故不正确;
故选A.
【点睛】本题考查了直线的性质,线段的中点,两点之间的距离,熟练掌握线段上的点把线段分成相等的两条线段,那么这个点是这条线段的中点是解答本题的关键.
6.D
【分析】根据线段的定义、以及射线的延伸性即可作出判断.
【详解】解:、射线是无限延伸的,故选项错误,不符合题意;
、线段的长度叫做它们间的距离,故选项错误,不符合题意;
、两点之间,线段最短,故选项错误,不符合题意;
、直线a,b相交于点P,说法正确,符合题意.
故选:D.
【点睛】本题考查了线段和射线的定义,解题的关键是理解射线的延伸性.
7.B
【分析】用三角板画出角,用角度加减法,根据选项一一分析,排除错误答案.
【详解】解:A. 的角,.
B.画不出 的角,
C. 的角,.
D. 的角,.
故选B.
【点睛】用三角板直接画特殊角的步骤:先画一条射线,再把三角板所画角的一边与射线重合,顶点与射线端点重合,最后沿另一边画一条射线,标出角的度数.
8.D
【分析】准确地找到对应的角度,关键是射线和南北方向之间的夹角,一一求出角度即可判断正误.
【详解】解:A、的方向是北偏东45度即东北方向,故正确,不符合题意;
B、的方向是北偏西,故正确,不符合题意;
C、的方向是南偏西,故正确,不符合题意;
D、的方向是南偏东,故错误,符合题意.
故选:D.
【点睛】本题主要考查了方位角的运用,解题的关键是会准确地找到所对应的角度是需要掌握的基本能力之一.
9.B
【分析】先根据余角的定义,求出∠AOC的度数,再根据角平分线的定义∠DOC的度数,即可求得∠BOD的度数.
【详解】解:∵∠AOC与∠COB互余,∠COB=15°,
∴∠AOC=90°﹣∠BOC=90°﹣15°=75°,
∵OC平分∠AOD,
∴∠DOC=∠AOC=75°,
∴∠BOD=∠DOC﹣∠BOC=75°﹣15°=60°,
故选:B.
【点睛】本题考查余角定义、角平分线的定义,熟知余角的定义是解答的关键.
10.A
【分析】根据时针与分针相距的份数乘以每份的度数,可得答案.
【详解】解:9:30时针与分针相距3.5份,每份的度数是30°,
在时刻9:30,时钟上时针和分针之间的夹角(小于平角的角)为3.5×30°=105°.
故选:A.
【点睛】本题考查了钟面角,利用时针与分针相距的份数乘以每份的度数是解题关键.
11.30
【详解】解:∵180°-150°=30°,
∴150°角的补角为30°.
故答案为:30.
【点睛】本题考查的是余角和补角的定义,如果两个角的和是一个直角,那么称这两个角互为余角.如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角.
12.2
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“1”与“x”是相对面,
“3”与“y”是相对面,
∵相对面上两个数互为相反数,
∴x=-1,y=-3,
∴x-y=(-1)-(-3)=-1+3=2.
故答案为:2.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
13.140
【详解】解:∵OD平分∠AOC,
∴∠AOC=2∠AOD=40°,
∴∠COB=180°﹣∠COA=140°
故答案为:140
14.60
【分析】设出所求的角为x,则它的补角为180°-x,余角为90°-x,根据题意列出方程,再解方程即可求解.
【详解】解:设这个角的度数是x,则它的补角为:180°-x,余角为90°-x;
由题意,得:(180°-x)-2(90°-x)=60°.
解得:x=60°.
答:这个角的度数是60°.
故答案为:60.
【点睛】本题考查了余角和补角的定义;根据角之间的互余和互补关系列出方程是解决问题的关键.
15.35
【分析】根据分别是的平分线.得出∠AOE=∠DOE,∠BOF=∠COF,可得∠AOE+∠BOF=∠DOE+∠COF=∠EOF-∠COD=155°-∠COD,根据周角∠AOB+∠AOE+∠BOF+∠EOF=360°,得出85°+155°-∠COD+155°=360°,解方程即可.
【详解】解:∵分别是的平分线.
∴∠AOE=∠DOE,∠BOF=∠COF,
∴∠AOE+∠BOF=∠DOE+∠COF=∠EOF-∠COD=155°-∠COD,
∵∠AOB+∠AOE+∠BOF+∠EOF=360°,
∴85°+155°-∠COD+155°=360°,
解得∠COD=35°.
故答案为35.
【点睛】本题考查角平分线有关的计算,角的和差,周角性质,一元一次方程,掌握角平分线有关的计算,角的和差,周角性质,一元一次方程是解题关键.
16..
【分析】根据角度的单位换算1°=60′,求出24′÷60′=0.4°即可.
【详解】解:∵1°=60′,
∴24÷60°=0.4°,
∴.
故答案为:.
【点睛】本题考查角度单位换算,掌握角的由大单位变小单位用乘法,由小单位变大单位用除法是解题关键.
17.>
【分析】构造等腰直角三角形,根据等腰直角三角形的性质即可进行比较大小.
【详解】解:如下图所示,
是等腰直角三角形,
∴,
∴.
故答案为
另:此题也可直接测量得到结果.
【点睛】本题考查等腰直角三角形的性质,构造等腰直角三角形是解题的关键.
18.(1)
(2)
【分析】(1)按照运算顺序,先算乘方,再算乘法,最后算加减,然后进行计算即可;
(2)根据度分秒的进制进行计算即可.
(1)
解:原式
.
(2)
解:原式
.
【点睛】本题考查了度分秒的换算,有理数的混合运算,准确熟练地进行计算是解题的关键.
19.见解析
【分析】在射线AP上依次截取AE=EF=a,在EF上截取FB=b,则线段AB满足条件.
【详解】解:如图,AB为所作;
【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
20.线段MN的长为15.
【分析】根据线段中点的定义和线段的和差倍分关系即可得到结论
【详解】解:∵AB:BC:CD=3:1:2,且AD=30,
∴AB=15,BC=5,AB=10,
∴AC= AB+BC=20,
∵点M是AC的中点,N是线段CD的中点,
∴MC=AC=10,CN=CD=5,
∴MN=MC+CN=15.
∴线段MN的长为15.
【点睛】本题考查了线段的中点和求两点之间的距离,能求出各个线段的长度是解此题的关键.
21.(1)见解析
(2)见解析
【分析】(1)根据题意作出线段,直线,射线即可;
(2)在线段上截取,点即为所求.
(1)
连接AC,面出直线AB,射线BC;如图所示,
(2)
如图,在线段上截取,点即为所求,
【点睛】本题考查了尺规作图-作线段等于已知线段,画线段、射线、直线,掌握线段、射线、直线的特点是解题的关键.
22.(1)
(2)OE平分,理由见解析
【分析】(1)根据,OC平分,可知;根据,可知,以此即可求出的度数;
(2)按照(1)求值的思路,将数字换为字母进行证明即可.
(1)
解OC平分,,
,
,
,
又,
;
(2)
OE平分,理由如下:
平分,,
,
又,
;
平分.
【点睛】本题主要考查的是角度的计算,角平分线的应用,熟练掌握角度之间的运算是解题的关键.
23.(1)BF∥DE,理由见解析;(2)60°
【分析】(1)由于∠AGF=∠ABC,可判断GF∥BC,则∠1=∠3,由∠1+∠2=180°,得出∠3+∠2=180°判断出BF∥DE;
(2)由∠2=150°得出∠1=30°,再根据垂直定义进而得出∠AFG的度数.
【详解】解:(1)BF∥DE.理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE;
(2)∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∵BF⊥AC
∴∠BFA=90°
∴∠AFG=90°﹣30°=60°.
【点睛】本题考查了平行线的判定与性质,解题的关键是掌握同位角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,内错角相等.
24.(1)110°
(2)100°
【分析】(1)由OM是∠AOB的角平分线,∠AOB=30°,得到,则∠BON=∠MON-∠BOM=55°,再由ON是∠BOC的角平分线,得到∠BOC=2∠BON=110°;
(2)设∠AOM=∠NOC=x,则∠AOB=4x,可推出∠BOM=3x,∠BOM:∠BON=3:2,得到∠BON=2x,根据∠AOC=∠AOB+∠BON+∠NOC=7x=140°,得到x=20°,则∠MON=∠BOM+∠BON=5x=100°.
(1)
解:∵OM是∠AOB的角平分线,∠AOB=30°,
∴,
∵∠MON=70°,
∴∠BON=∠MON-∠BOM=55°,
∵ON是∠BOC的角平分线,
∴∠BOC=2∠BON=110°;
(2)
解:设∠AOM=∠NOC=x,则∠AOB=4x,
∴∠BOM=∠AOB-∠AOM=3x,
∵∠BOM:∠BON=3:2,
∴∠BON=2x,
∴∠AOC=∠AOB+∠BON+∠NOC=7x=140°,
∴x=20°,
∴∠MON=∠BOM+∠BON=5x=100°.
【点睛】本题主要考查了几何中角度的计算,角平分线的定义,解题的关键在于能够熟练掌握相关知识.
25.(1),;(2);(3)50°或140°.
【分析】(1)根据,即可求解;
(2)先求出∠COM,再求出∠CON,相加即可求解;
(3)分当OD在内部和外部两种情况分类讨论即可求解.
【详解】解:(1)∵,
∴,
;
(2)∵平分,
∴,
∵ ,
∴,
∴ ;
(3)如图1,当OD在内部时,
∵,
∴∠BOD=,
∴∠COD=∠BOC-∠BOD=80°-30°=50°;
如图2,当OD在外部时,
∵,
∴∠BOD=,
∴∠COD=∠BOC+∠BOD=80°+60°=140°,
∴的度数为50°或140°.
.
【点睛】本题考查了角的计算,熟知角的特点和比例意义并根据题意画图求解是解题关键.
26.(1)120°,60°;(2)30°;(3)30°.
【分析】(1)点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,可以求得∠AOC和∠BOC的度数;
(2)根据∠AOC的度数和∠MON的度数可以得到∠CON的度数;
(3)根据∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,可以得到∠BON-∠COM的度数.
【详解】解:(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
【点睛】本题考查了角的计算,解题的关键是找出各个角之间的关系,与已知条件建立关系,然后求出所求角的度数.
27.(1)
(2)①2s;②s或s或s.
【分析】(1)利用角的和差关系可得从而可得答案;
(2)①先求解重合的时间,再画出图形,结合几何图形与角的和差关系列方程,再解方程即可;②分情况讨论:当时,结合①可得 当时, 当时,利用角的和差关系列方程 解方程即可,当时,如图,当 利用角的和差关系列方程 再解方程即可,当时, 当时,利用角的和差关系列方程,再解方程即可,从而可得答案.
【详解】(1)解: ,
(2)解:① 则重合时的时间为:(s),
当时,
解得:
所以当旋转2s时,
②当旋转到射线上时,(s),
当时,结合①可得
当重合时,(s),重合时,(s),如图,
所以当时,
当重合时,(s),如图,
当时,
平分
解得:
当重合时,(s),
当时,如图,
平分
解得: 不符合题意,舍去,
当重合时,(s),
当
平分
解得:
如图,当再次重合时,(s),
当时,
如图,当重合时,(s)
当时,
平分
解得:
综上:当时,s或s或s.
【点睛】本题考查的是几何图形中角的和差关系,角的动态定义的理解,一元一次方程的应用,“数形结合与利用一元一次方程解决动态几何问题”是解本题的关键.
28.(1)4°
(2)40°
【分析】(1)设 利用角平分线的定义可求得∠AOM=,∠DON,再根据列式求出,求出,再减去的度数,结论可得;
(2)根据角平分线的定义可求得∠AOM,∠BON,再利用角的和差得出结论.
(1)
设
∵
∴
∵是的平分线
∴;
∵
∴
∵是的平分线,
∴
∵
∴
解得,
∴
∴
∴
∵
∴
(2)
由图可得,
∵是的平分线
∴
又
∵是的平分线,
∴
∴
∵∠AOD=130°,∠BOC=50°,
∴
【点睛】本题主要考查了角的计算,角平分线的定义.本题是探究型题目,利用类比的方法解答是解题的关键.
