4.4.2 对数函数的图像和性质(第二课时) 课件(共21张PPT)
文档属性
| 名称 | 4.4.2 对数函数的图像和性质(第二课时) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 05:59:50 | ||
图片预览







文档简介
(共21张PPT)
人教A版高中数学必修第一册
对数函数的图象和性质
复习回顾
复习回顾
a>1 0<a<1
图 象
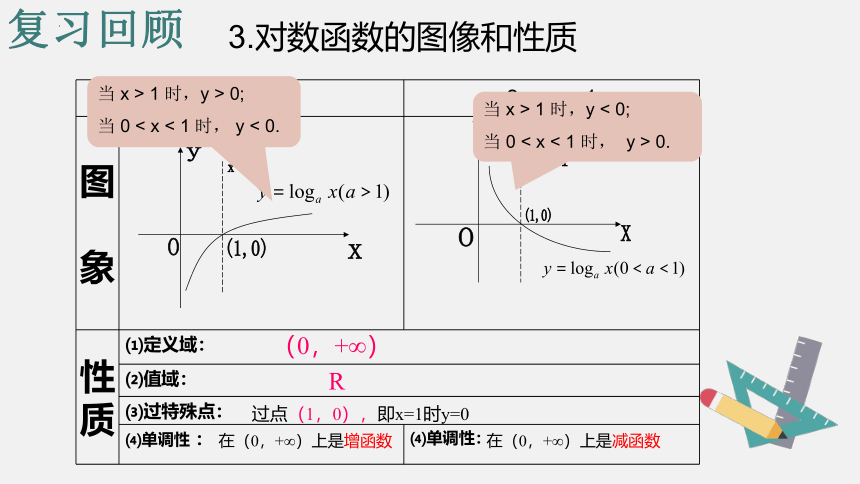
性 质 ⑴定义域: ⑵值域: ⑶过特殊点: ⑷单调性 : ⑷单调性:
(0,+∞)
R
过点(1,0),即x=1时y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
x
o
(1,0)
x =1
y
x
y
x = 1
(1,0)
o
当 x > 1 时,y > 0;
当 0 < x < 1 时, y < 0.
当 x > 1 时,y < 0;
当 0 < x < 1 时, y > 0.
3.对数函数的图像和性质
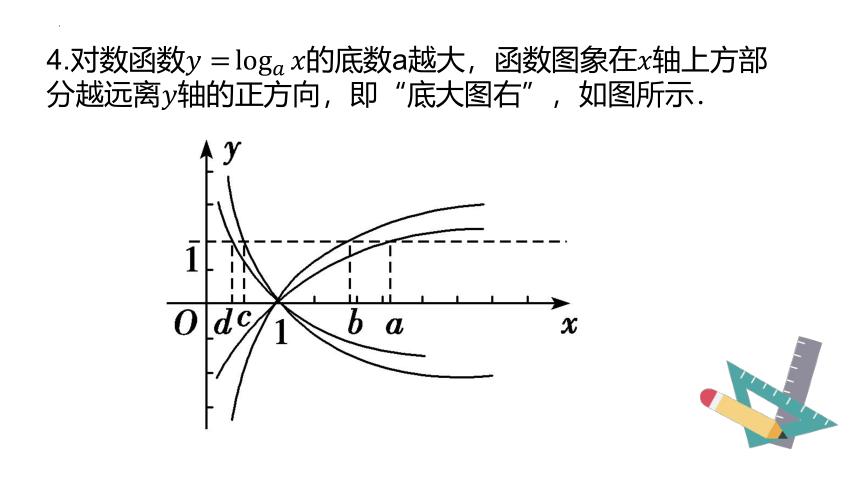
4.对数函数的底数a越大,函数图象在轴上方部分越远离轴的正方向,即“底大图右”,如图所示.
例题讲解
规律方法
对数值比较大小的常用方法
(1)如果同底,可直接利用单调性求解.如果底数为字母,则要分类讨论.
(2)如果不同底,一种方法是化为同底的,另一种方法是寻找中间变量.
(3)如果不同底但同真,可利用图象的高低与底数的大小解决或利用换底公式化为同底的再进行比较.
(4)若底数和真数都不相同,则常借助中间量1,0,-1等进行比较.
规律方法
即溶液中氢离子的浓度越大,溶液的酸性就越强.
~
概念讲解
因此,函数 y = logax (a>0,且a≠1)与指数函数y = ax互为反函数。
已知函数 y=2x (x∈R ,y ∈(0,+∞)) 可得到x=log2y ,对于任意一个y∈(0,+∞),通过式子x=log2y ,x在R中都有唯一确定的值和它对应。也就是说,可以把y作为自变量,x作为y的函数,这是我们就说x=log2y (y∈(0,+∞))是函数 y=2x ( x∈R) 的反函数。
但习惯上,我们通常用x表示自变量,y表示函数。为此我们常常对调函数x=log2y 中的字母x,y,把它写成y=log2x ,这样,对数函数y=log2x ( x∈(0,+∞) )是指数函数y=2x (x∈R )的反函数。
探究
(1)在同一坐标系内用描点法画出函数y=图象与y=的图象之后,说出这两个函数图象之间有什么关系?
提示:图象如图,图象关于y=x对称
(2)对数函数和指数函数中自变量和函数值的取值范围分别是什么?有什么关系?
提示:对数函数的自变量的取值范围即定义域与指数函数的值域取值范围相同,都为(0,+∞).对数函数的值域与指数函数中的自变量的取值范围即定义域相同,即为R.
一般地,指数函数y=(a>0,且a≠1)与对数函数y=(a>0,且a≠1)互为反函数,它们的定义域与值域正好互换.
特别提醒:互为反函数的两个函数图象关于y=x对称.
结论
练习
与函数的图象关于直线y=x对称的函数是( )
A.y= B.y= C.y= D.y=
例题讲解
例3 (1)解不等式;
例:(2)若,求实数a的取值范围.
跟踪训练
(1)若0,则a的取值范围是( )
A.(0,1) B.C. D.(1,+∞)
B
(2)解不等式:
例4 求函数的单调区间.
例题讲解
特别提醒:树立对数函数定义域优先的原则.
跟踪训练
求函数的单调区间.
课时小结
1.利用对数函数的性质比较大小
2.反函数及其性质、图象特征
3.求复合函数的单调性
感谢观看
祝学习进步
人教A版高中数学必修第一册
对数函数的图象和性质
复习回顾
复习回顾
a>1 0<a<1
图 象
性 质 ⑴定义域: ⑵值域: ⑶过特殊点: ⑷单调性 : ⑷单调性:
(0,+∞)
R
过点(1,0),即x=1时y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
x
o
(1,0)
x =1
y
x
y
x = 1
(1,0)
o
当 x > 1 时,y > 0;
当 0 < x < 1 时, y < 0.
当 x > 1 时,y < 0;
当 0 < x < 1 时, y > 0.
3.对数函数的图像和性质
4.对数函数的底数a越大,函数图象在轴上方部分越远离轴的正方向,即“底大图右”,如图所示.
例题讲解
规律方法
对数值比较大小的常用方法
(1)如果同底,可直接利用单调性求解.如果底数为字母,则要分类讨论.
(2)如果不同底,一种方法是化为同底的,另一种方法是寻找中间变量.
(3)如果不同底但同真,可利用图象的高低与底数的大小解决或利用换底公式化为同底的再进行比较.
(4)若底数和真数都不相同,则常借助中间量1,0,-1等进行比较.
规律方法
即溶液中氢离子的浓度越大,溶液的酸性就越强.
~
概念讲解
因此,函数 y = logax (a>0,且a≠1)与指数函数y = ax互为反函数。
已知函数 y=2x (x∈R ,y ∈(0,+∞)) 可得到x=log2y ,对于任意一个y∈(0,+∞),通过式子x=log2y ,x在R中都有唯一确定的值和它对应。也就是说,可以把y作为自变量,x作为y的函数,这是我们就说x=log2y (y∈(0,+∞))是函数 y=2x ( x∈R) 的反函数。
但习惯上,我们通常用x表示自变量,y表示函数。为此我们常常对调函数x=log2y 中的字母x,y,把它写成y=log2x ,这样,对数函数y=log2x ( x∈(0,+∞) )是指数函数y=2x (x∈R )的反函数。
探究
(1)在同一坐标系内用描点法画出函数y=图象与y=的图象之后,说出这两个函数图象之间有什么关系?
提示:图象如图,图象关于y=x对称
(2)对数函数和指数函数中自变量和函数值的取值范围分别是什么?有什么关系?
提示:对数函数的自变量的取值范围即定义域与指数函数的值域取值范围相同,都为(0,+∞).对数函数的值域与指数函数中的自变量的取值范围即定义域相同,即为R.
一般地,指数函数y=(a>0,且a≠1)与对数函数y=(a>0,且a≠1)互为反函数,它们的定义域与值域正好互换.
特别提醒:互为反函数的两个函数图象关于y=x对称.
结论
练习
与函数的图象关于直线y=x对称的函数是( )
A.y= B.y= C.y= D.y=
例题讲解
例3 (1)解不等式;
例:(2)若,求实数a的取值范围.
跟踪训练
(1)若0,则a的取值范围是( )
A.(0,1) B.C. D.(1,+∞)
B
(2)解不等式:
例4 求函数的单调区间.
例题讲解
特别提醒:树立对数函数定义域优先的原则.
跟踪训练
求函数的单调区间.
课时小结
1.利用对数函数的性质比较大小
2.反函数及其性质、图象特征
3.求复合函数的单调性
感谢观看
祝学习进步
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
