人教版选择性必修一 2.5 用单摆测重力加速度专题(含答案)
文档属性
| 名称 | 人教版选择性必修一 2.5 用单摆测重力加速度专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-01 10:11:48 | ||
图片预览


文档简介
人教版选择性必修一第二章用单摆测重力加速度专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
1. 在用单摆测量重力加速度的实验中,以下叙述正确的是
A. 为了摆的周期大一些,以方便测量,开始时拉开摆球,使摆角较大
B. 用刻度尺测量摆线的长度,这就是单摆的摆长
C. 摆球尽量选择质量大些、体积小些的
D. 用秒表测量周期时,应取摆球摆至最高点时开始计时,记下次全振动的时间,则单摆周期
2. 如图所示,在“用单摆测定重力加速度”的实验中,某同学发现他测量的重力加速度的值偏大,可能是下述哪个原因引起的( )
A. 以摆线长作为摆长来计算
B. 以摆线长与摆球的直径之和作为摆长来计算
C. 把次摆动的时间误记为次摆动的时间
D. 单摆的悬点未固定紧,振动中出现松动,使摆线增长了
3. 某同学在用单摆测定重力加速度的实验中,用的摆球密度不均匀,无法确定重心位置,他第一次测得悬线长,测得周期为;第二次测得悬线长为,测得周期为。根据上述数据,值应为( )
A. B. C. D. 无法计算
4. 某同学用单摆测当地的重力加速度.他测出了摆线长度和摆动周期,如图所示.通过改变悬线长度,测出对应的摆动周期,获得多组与,再以为纵轴、为横轴画出函数关系图像如图所示.由此种方法得到的重力加速度值与测实际摆长得到的重力加速度值相比会( )
A. 偏大 B. 偏小 C. 一样 D. 都有可能
5. 在用单摆测定重力加速度时,摆球应选用。( )
A. 半径为的木球 B. 半径为的铝球
C. 半径为的空心钢球 D. 半径为的实心钢球
6. 某同学在“用单摆测重力加速度”的实验中,由于没有游标卡尺,无法测小球的直径,实验中将悬点到小球最高点的距离作为摆长,测得多组周期和的数据,作出图象,由此可知( )
A. 该同学做出的图线应为图中所示
B. 由所作图线可知小球直径为
C. 采用本实验所测数据和,亦可用公式计算当地重力加速度
D. 由所作图线可知当地重力加速度大小约为
7. 用图示的装置做“用单摆测重力加速度”的实验。操作正确的是( )
A. 实验中应该在摆球摆动到最低点时开始计数
B. 组装单摆时,应该选用长度为左右的细线
C. 组装单摆时,应该选用直径约为的塑料球
D. 摆长测定后,摆动计数过程中摆线松动,对测量结果没影响
8. 某小组利用单摆测定当地重力加速度,最合理的装置是( )
A. B. C. D.
9. 甲、乙两位同学利用假期分别在两个地方做“用单摆测重力加速度”的实验,回来后共同绘制了--图像,如图甲中、所示,此外甲同学还顺便利用其实验的单摆探究了受迫振动,并绘制了单摆的共振曲线,如图乙所示,那么下列说法不正确的是( )
A. 单摆的固有周期由摆长和所处环境的重力加速度共同决定
B. 由图甲分析可知,图线所对应的实验地点重力加速度较大
C. 若将单摆放入绕地球稳定飞行的宇宙飞船中,则无法利用单摆测出飞船轨道处的重力加速度
D. 如果甲同学增大摆长,他得到的共振曲线的峰将向左移动
10. 甲、乙两位同学在同一实验室做沙摆实验,以相同速度拉动纸板,在相同长度的纸板上得到的痕迹图象,如图所示,下列说法不正确的是( )
A. 沙摆质量的变化对周期的影响较小,可以忽略不计
B. 甲、乙两个沙摆的周期之比为
C. 甲、乙两个沙摆的等效摆长为
D. 在误差范围内,甲、乙两同学测得的重力加速度的数值相同
二、实验题(本大题共3小题,共40.0分)
11. 小华同学在做“用单摆测定重力加速度”的实验。
用游标卡尺测小球的直径时示数如图甲所示,则小球的直径________。
如图乙所示,搭建实验装置时,要用铁夹夹住摆线上端,这样做的主要目的是________。
A.便于测量单摆摆长 便于测量单摆周期
C.确保摆动时摆长不变 确保摆球在竖直平面内摆动
小华同学用标准的实验器材和正确的实验方法测量出几组不同摆长和对应的周期,然后根据数据描绘图像,进一步计算得到图线的斜率为,可知当地的重力加速度大小________。
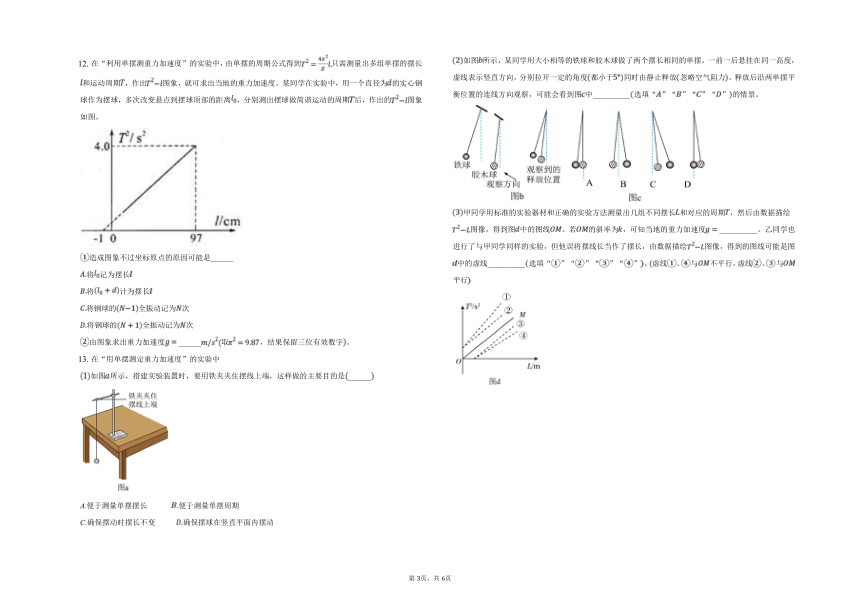
12. 在“利用单摆测重力加速度”的实验中,由单摆的周期公式得到只需测量出多组单摆的摆长和运动周期,作出图象,就可求出当地的重力加速度。某同学在实验中,用一个直径为的实心钢球作为摆球,多次改变悬点到摆球顶部的距离,分别测出摆球做简谐运动的周期后,作出的图象如图。
造成图象不过坐标原点的原因可能是______
将记为摆长
将计为摆长
将钢球的全振动记为次
将钢球的全振动记为次
由图象求出重力加速度______取,结果保留三位有效数字。
13. 在“用单摆测定重力加速度”的实验中
如图所示,搭建实验装置时,要用铁夹夹住摆线上端,这样做的主要目的是______
A.便于测量单摆摆长 便于测量单摆周期
C.确保摆动时摆长不变 确保摆球在竖直平面内摆动
如图所示,某同学用大小相等的铁球和胶木球做了两个摆长相同的单摆,一前一后悬挂在同一高度,虚线表示竖直方向,分别拉开一定的角度都小于同时由静止释放忽略空气阻力。释放后沿两单摆平衡位置的连线方向观察,可能会看到图中__________选填“”“”“”“”的情景。
甲同学用标准的实验器材和正确的实验方法测量出几组不同摆长和对应的周期,然后由数据描绘图像,得到图中的图线。若的斜率为,可知当地的重力加速度__________。乙同学也进行了与甲同学同样的实验,但他误将摆线长当作了摆长,由数据描绘图像,得到的图线可能是图中的虚线__________选填“”“”“”“”。虚线、与不平行,虚线、与平行
答案和解析
1.【答案】
【解析】
【分析】
为减小实验误差,应选择质量大而体积小的球作为摆球;摆线长度与摆球半径之和是单摆摆长;应选择伸缩性小的细线当摆线,单摆完成一次全振动需要的时间是一个周期,根据实验注意事项分析答题。
【解答】
A、单摆在摆角小于时的运动是简谐振动,实验时摆角不能太大,故A错误;
B、摆线长度与摆球半径之和是单摆摆长,用刻度尺测量摆线的长度,摆线长度不是摆长,故B错误;
C、为减小空气阻力对实验的影响,摆球尽量选择质量大些、体积小些的,故C正确;
D、为减小周期测量误差,释放摆球,应从摆球经过平衡位置开始计时,记下摆球做次全振动所用的时间,则单摆周期为,故D错误。
2.【答案】
【解析】
【分析】
根据单摆周期公式求出重力加速度的表达式,根据重力加速度表达式分析各选项答题。
本题考查了应用单摆测重力加速度实验的实验误差分析,知道用单摆测重力加速度的实验原理是单摆周期公式是解题的前提,应用单摆周期公式求出重力加速度的表达式即可解题。
【解答】
解:由单摆周期公式:可知,重力加速度:;
A、以摆线长作为摆长,摆长偏小,所测重力加速度偏小,故A错误;
B、以摆线长与摆球的直径之和作为摆长,所测摆长偏大,所测重力加速度偏大,故B正确;
C、把次摆动的时间误记为次摆动的时间,所测周期偏大,所测重力加速度偏小,故C错误;
D、单摆的悬点未固定紧,振动中出现松动,使摆线增长了,所测周期偏大,所测重力加速度偏小,故D错误。
故选B。
3.【答案】
【解析】
【分析】
本题运用单摆周期公式分析处理实际问题,注意单摆的摆长等于摆球的重心到悬点的距离,不是摆线的长度。
设摆球的重心到线与球结点的距离为,根据单摆周期的公式分别列出方程,求解重力加速度。
【解答】
解:设悬线与球上表面接触处到球重心的距离为,则
第一次:
第二次:
由两式消去得,B正确,ACD错误。
故选B。
4.【答案】
【解析】
【分析】
由实验中所得到的关系图象,由斜率分析重力加速度。
明确实验注意事项,知道图象斜率截距的意义,这一点很重要,同时掌握单摆的周期公式,及图象的物理意义。
【解答】
由,,得:,测出了摆线长度和摆动周期,用的关系图线求当地重力加速度值,由于图象的斜率不受影响,所以与重力加速度实际值一样,故C正确;
故选:。
5.【答案】
【解析】略
6.【答案】
【解析】解:由单摆周期公式得:。
A、根据关系可知图象与纵坐标的截距为负值,该同学做出的图线应为图中所示,故A错误;
B、因截距为,解得小球的直径为,故B错误;
C、原因是悬点到小球最高点的距离,所以不能采用本实验所测数据和,根据公式计算当地重力加速度,故C错误;
D、由数学关系得图象的斜率为:,解得重力加速度为:,故D正确。
故选:。
由重力加速度的表达式求得的关系式,根据数学知识分析图象的图线斜率及截距的意义,由此求出小球的直径和当地的重力加速度。
本题重点为考查摆长、周期等物理量之间的关系,解决本题的关键知道该实验的原理,掌握单摆的周期公式,会通过图象法求解重力加速度的大小。
7.【答案】
【解析】解:、实验计数应在摆球摆到最低点开始,最低点时运动速度最大,位置变化较明确,可减小单摆周期的测量误差,故A正确;
B、组装单摆时一般选择左右的细线,故B错误;
C、为减小空气阻力的影响,摆球应选择密度大体积小的钢球,故C错误;
D、摆动计数过程中摆线松动,会引起摆线变化,对实验结果有影响,故D错误。
故选:。
为了减小误差,应该选用相对较长的细线,为减小空气阻力对实验的影响,应选择质量大而体积小的球做摆球;计数应在摆球最低点时开始,摆线松动会引起的变化,从而对结果有影响。
解决该题的关键是明确实验原理,了解实验器材的操作过程,重点需掌握如何计算单摆的周期。
8.【答案】
【解析】解:根据单摆理想化模型可知,为减少空气阻力的影响,摆球应采用密度较大,体积小的铁球;为使摆动时摆长不变化,摆线应用不易形变的细丝线,悬点应用铁夹来固定,故最合理的为,故D正确,ABC错误。
故选:。
明确简谐运动的性质,知道单摆是理想化的物理模型并明确摆线质量不计、且长度不能形变,且小球体积小,质量大。
解决该题的关键是明确知道单摆的定义以及其组成结构,明确如何构造一个最合理的单摆。
9.【答案】
【解析】分析:根据单摆的周期公式变形得到与的关系式,再根据数学知识研究图象的斜率与重力加速度的关系;
解答:根据单摆的固有周期公式,摆长为,,所处环境的重力加速度为,故说法A正确;
根据单摆的周期公式得:,由数学知识得知,图象的斜率,由图甲分析可知,图线的斜率较大,那么所对应的实验地点重力加速度较小,故说法B错误;
若将单摆放入绕地球稳定飞行的宇宙飞船中,单摆小球处于完全失重状态,只受重力,不能在竖直平面内来回摆动,则无法利用单摆测出飞船轨道处的重力加速度,故说法C正确;
根据单摆的固有周期公式,如果甲同学增大摆长,则单摆的固有周期变大,固有频率变小,则发生共振时的驱动力变小,得到的共振曲线的峰将向左移动,故说法D正确;
那么说法不正确的是。
10.【答案】
【解析】
【分析】
单摆周期与质量无关;根据图像求得周期,再根据求得等效摆长;在地球上同一地点,重力加速度相同。
【解答】
A.由可知,单摆周期与质量无关,在沙摆摆动、沙子逐渐下漏的过程中,摆的重心虽然变化,但是摆长远远大于摆的重心位置变化,所以沙摆质量的变化对周期的影响较小,可以忽略不计,故A正确;
设拉动纸板速度为,分析图可知,甲图周期为,乙图周期为,故甲、乙两个沙摆的周期之比为,由可得:,故甲、乙两个沙摆的等效摆长为,故B正确,C错误;
D.同一地点的重力加速度是相同的,在误差范围内,甲、乙两同学测得的重力加速度的数值相同,故D正确。
11.【答案】;
;
【解析】
【分析】
本题主要考查“用单摆测定重力加速度”的实验,明确实验原理和注意事项是解题的关键。
根据游标卡尺的读数方法可求得小球的直径;
根据实验原理和注意事项分析即可;
根据单摆周期公式,整理得到与的关系式,结合图线的斜率即可求得当地的重力加速度大小。
【解答】
游标卡尺的读数即小球的直径;
用铁夹夹牢摆线,是为了防止摆动过程中摆长的变化,如果需要改变摆长来探究摆长与周期关系时,方便调节摆长,所以用铁夹夹住摆线上端主要目的是确保摆动时摆长不变,故A、、D错误,C正确;
根据单摆周期公式,解得,根据数学知识可知,图线的斜率,则。
12.【答案】;
。
【解析】
【分析】
本题考查了应用单摆测重力加速度实验,熟练应用单摆周期公式是正确解题的关键;根据单摆周期公式求出图象的函数表达式是正确分析实验误差的关键。
【解答】
图象不通过坐标原点,将图象向右平移就会通过坐标原点,故相同的周期下,摆长偏小,故可能是测摆长时漏掉了摆球的半径;将记为摆长;故选A;
由单摆周期公式得:
则图象的斜率:
解得:;
13.【答案】; ; ; 。
【解析】
【分析】
本题根据单摆周期公式结合图示分析即可,难度不大。
【解答】
用铁夹牢摆线,是为了防止摆动过程中摆长发生变化,故选C。
由单摆周期公式可知两球周期相等,两单摆均由左侧由静止释放,则应同时到达平衡位置,同时到达同一侧的最大位移处,故ABD错误,C正确。
由单摆周期公式可知,,图线的斜率,故
乙同学误将摆线长当作了摆长,忘了加上摆球的半径,则应为,即原图线斜率不变,向左平移,即。
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
1. 在用单摆测量重力加速度的实验中,以下叙述正确的是
A. 为了摆的周期大一些,以方便测量,开始时拉开摆球,使摆角较大
B. 用刻度尺测量摆线的长度,这就是单摆的摆长
C. 摆球尽量选择质量大些、体积小些的
D. 用秒表测量周期时,应取摆球摆至最高点时开始计时,记下次全振动的时间,则单摆周期
2. 如图所示,在“用单摆测定重力加速度”的实验中,某同学发现他测量的重力加速度的值偏大,可能是下述哪个原因引起的( )
A. 以摆线长作为摆长来计算
B. 以摆线长与摆球的直径之和作为摆长来计算
C. 把次摆动的时间误记为次摆动的时间
D. 单摆的悬点未固定紧,振动中出现松动,使摆线增长了
3. 某同学在用单摆测定重力加速度的实验中,用的摆球密度不均匀,无法确定重心位置,他第一次测得悬线长,测得周期为;第二次测得悬线长为,测得周期为。根据上述数据,值应为( )
A. B. C. D. 无法计算
4. 某同学用单摆测当地的重力加速度.他测出了摆线长度和摆动周期,如图所示.通过改变悬线长度,测出对应的摆动周期,获得多组与,再以为纵轴、为横轴画出函数关系图像如图所示.由此种方法得到的重力加速度值与测实际摆长得到的重力加速度值相比会( )
A. 偏大 B. 偏小 C. 一样 D. 都有可能
5. 在用单摆测定重力加速度时,摆球应选用。( )
A. 半径为的木球 B. 半径为的铝球
C. 半径为的空心钢球 D. 半径为的实心钢球
6. 某同学在“用单摆测重力加速度”的实验中,由于没有游标卡尺,无法测小球的直径,实验中将悬点到小球最高点的距离作为摆长,测得多组周期和的数据,作出图象,由此可知( )
A. 该同学做出的图线应为图中所示
B. 由所作图线可知小球直径为
C. 采用本实验所测数据和,亦可用公式计算当地重力加速度
D. 由所作图线可知当地重力加速度大小约为
7. 用图示的装置做“用单摆测重力加速度”的实验。操作正确的是( )
A. 实验中应该在摆球摆动到最低点时开始计数
B. 组装单摆时,应该选用长度为左右的细线
C. 组装单摆时,应该选用直径约为的塑料球
D. 摆长测定后,摆动计数过程中摆线松动,对测量结果没影响
8. 某小组利用单摆测定当地重力加速度,最合理的装置是( )
A. B. C. D.
9. 甲、乙两位同学利用假期分别在两个地方做“用单摆测重力加速度”的实验,回来后共同绘制了--图像,如图甲中、所示,此外甲同学还顺便利用其实验的单摆探究了受迫振动,并绘制了单摆的共振曲线,如图乙所示,那么下列说法不正确的是( )
A. 单摆的固有周期由摆长和所处环境的重力加速度共同决定
B. 由图甲分析可知,图线所对应的实验地点重力加速度较大
C. 若将单摆放入绕地球稳定飞行的宇宙飞船中,则无法利用单摆测出飞船轨道处的重力加速度
D. 如果甲同学增大摆长,他得到的共振曲线的峰将向左移动
10. 甲、乙两位同学在同一实验室做沙摆实验,以相同速度拉动纸板,在相同长度的纸板上得到的痕迹图象,如图所示,下列说法不正确的是( )
A. 沙摆质量的变化对周期的影响较小,可以忽略不计
B. 甲、乙两个沙摆的周期之比为
C. 甲、乙两个沙摆的等效摆长为
D. 在误差范围内,甲、乙两同学测得的重力加速度的数值相同
二、实验题(本大题共3小题,共40.0分)
11. 小华同学在做“用单摆测定重力加速度”的实验。
用游标卡尺测小球的直径时示数如图甲所示,则小球的直径________。
如图乙所示,搭建实验装置时,要用铁夹夹住摆线上端,这样做的主要目的是________。
A.便于测量单摆摆长 便于测量单摆周期
C.确保摆动时摆长不变 确保摆球在竖直平面内摆动
小华同学用标准的实验器材和正确的实验方法测量出几组不同摆长和对应的周期,然后根据数据描绘图像,进一步计算得到图线的斜率为,可知当地的重力加速度大小________。
12. 在“利用单摆测重力加速度”的实验中,由单摆的周期公式得到只需测量出多组单摆的摆长和运动周期,作出图象,就可求出当地的重力加速度。某同学在实验中,用一个直径为的实心钢球作为摆球,多次改变悬点到摆球顶部的距离,分别测出摆球做简谐运动的周期后,作出的图象如图。
造成图象不过坐标原点的原因可能是______
将记为摆长
将计为摆长
将钢球的全振动记为次
将钢球的全振动记为次
由图象求出重力加速度______取,结果保留三位有效数字。
13. 在“用单摆测定重力加速度”的实验中
如图所示,搭建实验装置时,要用铁夹夹住摆线上端,这样做的主要目的是______
A.便于测量单摆摆长 便于测量单摆周期
C.确保摆动时摆长不变 确保摆球在竖直平面内摆动
如图所示,某同学用大小相等的铁球和胶木球做了两个摆长相同的单摆,一前一后悬挂在同一高度,虚线表示竖直方向,分别拉开一定的角度都小于同时由静止释放忽略空气阻力。释放后沿两单摆平衡位置的连线方向观察,可能会看到图中__________选填“”“”“”“”的情景。
甲同学用标准的实验器材和正确的实验方法测量出几组不同摆长和对应的周期,然后由数据描绘图像,得到图中的图线。若的斜率为,可知当地的重力加速度__________。乙同学也进行了与甲同学同样的实验,但他误将摆线长当作了摆长,由数据描绘图像,得到的图线可能是图中的虚线__________选填“”“”“”“”。虚线、与不平行,虚线、与平行
答案和解析
1.【答案】
【解析】
【分析】
为减小实验误差,应选择质量大而体积小的球作为摆球;摆线长度与摆球半径之和是单摆摆长;应选择伸缩性小的细线当摆线,单摆完成一次全振动需要的时间是一个周期,根据实验注意事项分析答题。
【解答】
A、单摆在摆角小于时的运动是简谐振动,实验时摆角不能太大,故A错误;
B、摆线长度与摆球半径之和是单摆摆长,用刻度尺测量摆线的长度,摆线长度不是摆长,故B错误;
C、为减小空气阻力对实验的影响,摆球尽量选择质量大些、体积小些的,故C正确;
D、为减小周期测量误差,释放摆球,应从摆球经过平衡位置开始计时,记下摆球做次全振动所用的时间,则单摆周期为,故D错误。
2.【答案】
【解析】
【分析】
根据单摆周期公式求出重力加速度的表达式,根据重力加速度表达式分析各选项答题。
本题考查了应用单摆测重力加速度实验的实验误差分析,知道用单摆测重力加速度的实验原理是单摆周期公式是解题的前提,应用单摆周期公式求出重力加速度的表达式即可解题。
【解答】
解:由单摆周期公式:可知,重力加速度:;
A、以摆线长作为摆长,摆长偏小,所测重力加速度偏小,故A错误;
B、以摆线长与摆球的直径之和作为摆长,所测摆长偏大,所测重力加速度偏大,故B正确;
C、把次摆动的时间误记为次摆动的时间,所测周期偏大,所测重力加速度偏小,故C错误;
D、单摆的悬点未固定紧,振动中出现松动,使摆线增长了,所测周期偏大,所测重力加速度偏小,故D错误。
故选B。
3.【答案】
【解析】
【分析】
本题运用单摆周期公式分析处理实际问题,注意单摆的摆长等于摆球的重心到悬点的距离,不是摆线的长度。
设摆球的重心到线与球结点的距离为,根据单摆周期的公式分别列出方程,求解重力加速度。
【解答】
解:设悬线与球上表面接触处到球重心的距离为,则
第一次:
第二次:
由两式消去得,B正确,ACD错误。
故选B。
4.【答案】
【解析】
【分析】
由实验中所得到的关系图象,由斜率分析重力加速度。
明确实验注意事项,知道图象斜率截距的意义,这一点很重要,同时掌握单摆的周期公式,及图象的物理意义。
【解答】
由,,得:,测出了摆线长度和摆动周期,用的关系图线求当地重力加速度值,由于图象的斜率不受影响,所以与重力加速度实际值一样,故C正确;
故选:。
5.【答案】
【解析】略
6.【答案】
【解析】解:由单摆周期公式得:。
A、根据关系可知图象与纵坐标的截距为负值,该同学做出的图线应为图中所示,故A错误;
B、因截距为,解得小球的直径为,故B错误;
C、原因是悬点到小球最高点的距离,所以不能采用本实验所测数据和,根据公式计算当地重力加速度,故C错误;
D、由数学关系得图象的斜率为:,解得重力加速度为:,故D正确。
故选:。
由重力加速度的表达式求得的关系式,根据数学知识分析图象的图线斜率及截距的意义,由此求出小球的直径和当地的重力加速度。
本题重点为考查摆长、周期等物理量之间的关系,解决本题的关键知道该实验的原理,掌握单摆的周期公式,会通过图象法求解重力加速度的大小。
7.【答案】
【解析】解:、实验计数应在摆球摆到最低点开始,最低点时运动速度最大,位置变化较明确,可减小单摆周期的测量误差,故A正确;
B、组装单摆时一般选择左右的细线,故B错误;
C、为减小空气阻力的影响,摆球应选择密度大体积小的钢球,故C错误;
D、摆动计数过程中摆线松动,会引起摆线变化,对实验结果有影响,故D错误。
故选:。
为了减小误差,应该选用相对较长的细线,为减小空气阻力对实验的影响,应选择质量大而体积小的球做摆球;计数应在摆球最低点时开始,摆线松动会引起的变化,从而对结果有影响。
解决该题的关键是明确实验原理,了解实验器材的操作过程,重点需掌握如何计算单摆的周期。
8.【答案】
【解析】解:根据单摆理想化模型可知,为减少空气阻力的影响,摆球应采用密度较大,体积小的铁球;为使摆动时摆长不变化,摆线应用不易形变的细丝线,悬点应用铁夹来固定,故最合理的为,故D正确,ABC错误。
故选:。
明确简谐运动的性质,知道单摆是理想化的物理模型并明确摆线质量不计、且长度不能形变,且小球体积小,质量大。
解决该题的关键是明确知道单摆的定义以及其组成结构,明确如何构造一个最合理的单摆。
9.【答案】
【解析】分析:根据单摆的周期公式变形得到与的关系式,再根据数学知识研究图象的斜率与重力加速度的关系;
解答:根据单摆的固有周期公式,摆长为,,所处环境的重力加速度为,故说法A正确;
根据单摆的周期公式得:,由数学知识得知,图象的斜率,由图甲分析可知,图线的斜率较大,那么所对应的实验地点重力加速度较小,故说法B错误;
若将单摆放入绕地球稳定飞行的宇宙飞船中,单摆小球处于完全失重状态,只受重力,不能在竖直平面内来回摆动,则无法利用单摆测出飞船轨道处的重力加速度,故说法C正确;
根据单摆的固有周期公式,如果甲同学增大摆长,则单摆的固有周期变大,固有频率变小,则发生共振时的驱动力变小,得到的共振曲线的峰将向左移动,故说法D正确;
那么说法不正确的是。
10.【答案】
【解析】
【分析】
单摆周期与质量无关;根据图像求得周期,再根据求得等效摆长;在地球上同一地点,重力加速度相同。
【解答】
A.由可知,单摆周期与质量无关,在沙摆摆动、沙子逐渐下漏的过程中,摆的重心虽然变化,但是摆长远远大于摆的重心位置变化,所以沙摆质量的变化对周期的影响较小,可以忽略不计,故A正确;
设拉动纸板速度为,分析图可知,甲图周期为,乙图周期为,故甲、乙两个沙摆的周期之比为,由可得:,故甲、乙两个沙摆的等效摆长为,故B正确,C错误;
D.同一地点的重力加速度是相同的,在误差范围内,甲、乙两同学测得的重力加速度的数值相同,故D正确。
11.【答案】;
;
【解析】
【分析】
本题主要考查“用单摆测定重力加速度”的实验,明确实验原理和注意事项是解题的关键。
根据游标卡尺的读数方法可求得小球的直径;
根据实验原理和注意事项分析即可;
根据单摆周期公式,整理得到与的关系式,结合图线的斜率即可求得当地的重力加速度大小。
【解答】
游标卡尺的读数即小球的直径;
用铁夹夹牢摆线,是为了防止摆动过程中摆长的变化,如果需要改变摆长来探究摆长与周期关系时,方便调节摆长,所以用铁夹夹住摆线上端主要目的是确保摆动时摆长不变,故A、、D错误,C正确;
根据单摆周期公式,解得,根据数学知识可知,图线的斜率,则。
12.【答案】;
。
【解析】
【分析】
本题考查了应用单摆测重力加速度实验,熟练应用单摆周期公式是正确解题的关键;根据单摆周期公式求出图象的函数表达式是正确分析实验误差的关键。
【解答】
图象不通过坐标原点,将图象向右平移就会通过坐标原点,故相同的周期下,摆长偏小,故可能是测摆长时漏掉了摆球的半径;将记为摆长;故选A;
由单摆周期公式得:
则图象的斜率:
解得:;
13.【答案】; ; ; 。
【解析】
【分析】
本题根据单摆周期公式结合图示分析即可,难度不大。
【解答】
用铁夹牢摆线,是为了防止摆动过程中摆长发生变化,故选C。
由单摆周期公式可知两球周期相等,两单摆均由左侧由静止释放,则应同时到达平衡位置,同时到达同一侧的最大位移处,故ABD错误,C正确。
由单摆周期公式可知,,图线的斜率,故
乙同学误将摆线长当作了摆长,忘了加上摆球的半径,则应为,即原图线斜率不变,向左平移,即。
第1页,共1页
