圆周角与圆心角的关系导学案
图片预览

文档简介
九年级数学导学案
温馨寄语: 人生不可能总是顺心如意,但持续朝着阳光走,影子就会躲在后面
课题 3.3圆周角与圆心角的关系 使用人 时间
课型 新课 课时数 1
学习目标 1. 了解圆周角的概念; 经历探索圆周角和圆心角的关系的过程, 理解和掌握圆周角定理;2. 通过探索圆周角与圆心角的关系, 体会分类、转化、归纳等数学思想方法
重点.难点 重点:圆周角和圆心角的关系 难点:圆周角和圆心角的关系
教学流程 教师个人添加(学生学习记录)
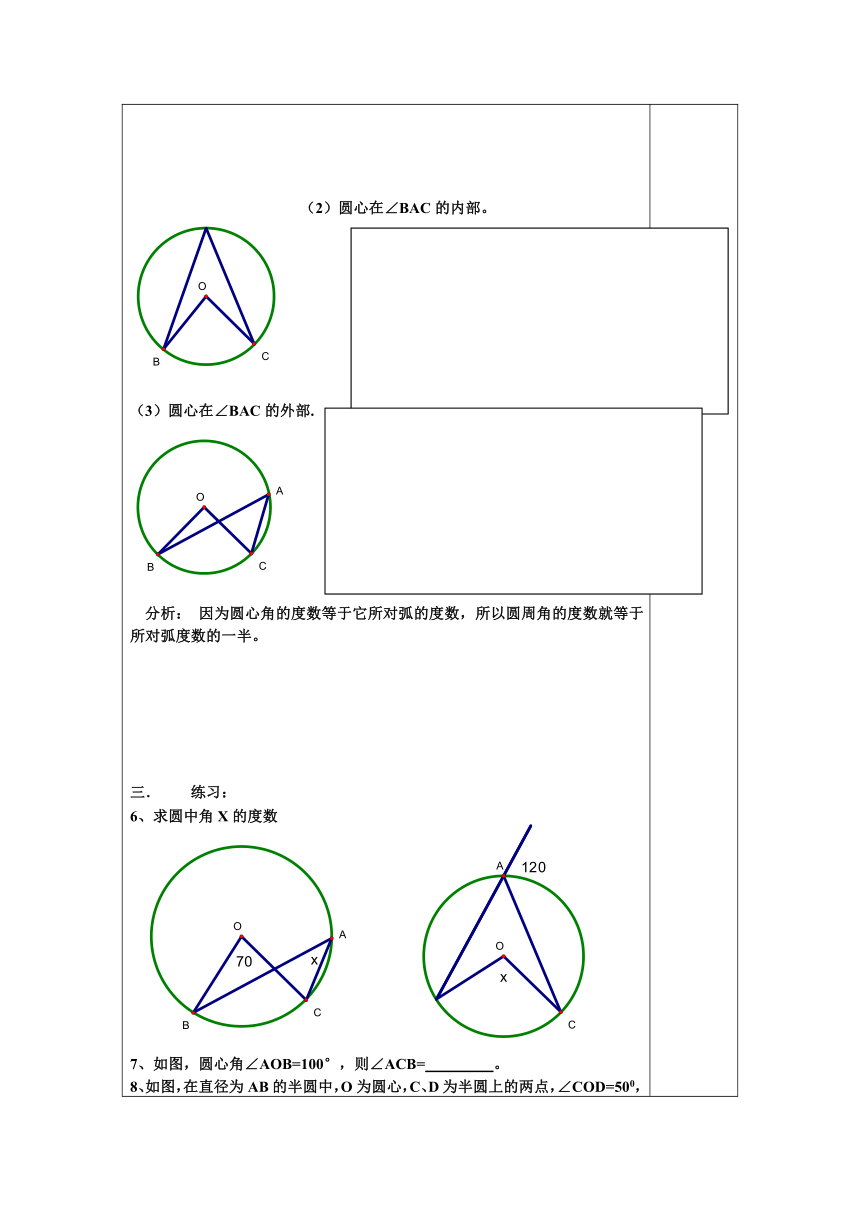
一、复习引入1、圆心角的定义 。2、在同圆或等圆中,圆心角的度数和它所对的弧的度数的关系 。圆周角与圆心角3、圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。圆周角:角的顶点在圆上,两边是圆的两条弦圆心角:角的顶点是圆心,两边是圆的两条半径 4.下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。 5.定理证明:(1)圆心在∠BAC的一边上。(2)圆心在∠BAC的内部。(3)圆心在∠BAC的外部. 分析: 因为圆心角的度数等于它所对弧的度数,所以圆周角的度数就等于所对弧度数的一半。练习:6、求圆中角X的度数 7、如图,圆心角∠AOB=100°,则∠ACB= 。8、如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________。12、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)0和(5x-30)0,则这条弧的度数为 。9、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=23°,求∠BOC的度数。
10.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度. (4) (5) (6)11.如图5,AB是⊙O的直径, ,∠A=25°,则∠BOD的度数为________.12.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.二、选择题:13.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( ) A.50° B.100° C.130° D.200° (7) (8) (9) (10)14.如图8,A、B、C、D四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对15.如图9,D是的中点,则图中与∠ABD相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个16.如图10,∠AOB=100°,则∠A+∠B等于( ) A.100° B.80° C.50° D.40°
教学反思(学生学习总结)
定理:一条弧所对的圆周角等于它所对的圆心角的一半。
证明过程:
_
C
_
B
_
A
_
O
_
D
_
C
_
B
_
A
温馨寄语: 人生不可能总是顺心如意,但持续朝着阳光走,影子就会躲在后面
课题 3.3圆周角与圆心角的关系 使用人 时间
课型 新课 课时数 1
学习目标 1. 了解圆周角的概念; 经历探索圆周角和圆心角的关系的过程, 理解和掌握圆周角定理;2. 通过探索圆周角与圆心角的关系, 体会分类、转化、归纳等数学思想方法
重点.难点 重点:圆周角和圆心角的关系 难点:圆周角和圆心角的关系
教学流程 教师个人添加(学生学习记录)
一、复习引入1、圆心角的定义 。2、在同圆或等圆中,圆心角的度数和它所对的弧的度数的关系 。圆周角与圆心角3、圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。圆周角:角的顶点在圆上,两边是圆的两条弦圆心角:角的顶点是圆心,两边是圆的两条半径 4.下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。 5.定理证明:(1)圆心在∠BAC的一边上。(2)圆心在∠BAC的内部。(3)圆心在∠BAC的外部. 分析: 因为圆心角的度数等于它所对弧的度数,所以圆周角的度数就等于所对弧度数的一半。练习:6、求圆中角X的度数 7、如图,圆心角∠AOB=100°,则∠ACB= 。8、如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________。12、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)0和(5x-30)0,则这条弧的度数为 。9、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=23°,求∠BOC的度数。
10.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度. (4) (5) (6)11.如图5,AB是⊙O的直径, ,∠A=25°,则∠BOD的度数为________.12.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.二、选择题:13.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( ) A.50° B.100° C.130° D.200° (7) (8) (9) (10)14.如图8,A、B、C、D四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对15.如图9,D是的中点,则图中与∠ABD相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个16.如图10,∠AOB=100°,则∠A+∠B等于( ) A.100° B.80° C.50° D.40°
教学反思(学生学习总结)
定理:一条弧所对的圆周角等于它所对的圆心角的一半。
证明过程:
_
C
_
B
_
A
_
O
_
D
_
C
_
B
_
A
