北师大版数学七年级上册 3.5 探索与表达规律(第2课时 表达规律)课件(共16张PPT)
文档属性
| 名称 | 北师大版数学七年级上册 3.5 探索与表达规律(第2课时 表达规律)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 538.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第三章 整式及其加减
5 探究与表达规律
第三章 整式及其加减
第2课时 表达规律
1
2
会用代数式表达规律,能利用代数式的运算解释具体问题中蕴含的一般规律及现象.(重难点)
在解决问题的过程中体验归纳、分析、猜想、抽象、类比、转化等思维方法,发展抽象思维能力.(难点)
学 习 目 标
新 课 导 入
做一个游戏,游戏规则如下:
教师背对学生,学生按下列四个步骤操作:
第一步:分发左、中、右三堆张数相同的牌(每堆牌不少于2张);
第二步:从左边拿出2张,放入中间;
第三步:从右边拿出1张,放入中间;
第四步:左边现在有几张牌,就从中间拿几张牌放入左边.
只要你按照上述步骤做,我就能准确地说出中间一堆牌现有的张数.
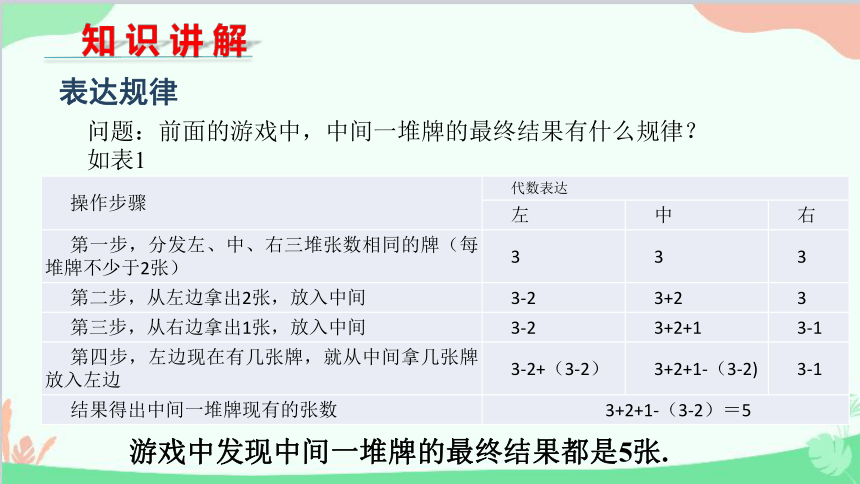
知 识 讲 解
表达规律
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) 3 3 3
第二步,从左边拿出2张,放入中间 3-2 3+2 3
第三步,从右边拿出1张,放入中间 3-2 3+2+1 3-1
第四步,左边现在有几张牌,就从中间拿几张牌放入左边 3-2+(3-2) 3+2+1-(3-2) 3-1
结果得出中间一堆牌现有的张数 3+2+1-(3-2)=5
问题:前面的游戏中,中间一堆牌的最终结果有什么规律?
如表1
游戏中发现中间一堆牌的最终结果都是5张.
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) a a a
第二步,从左边拿出2张,放入中间
第三步,从右边拿出1张,放入中间
第四步,左边现在有几张牌,就从中间拿几张牌放入左边
结果得出中间一堆牌现有的张数
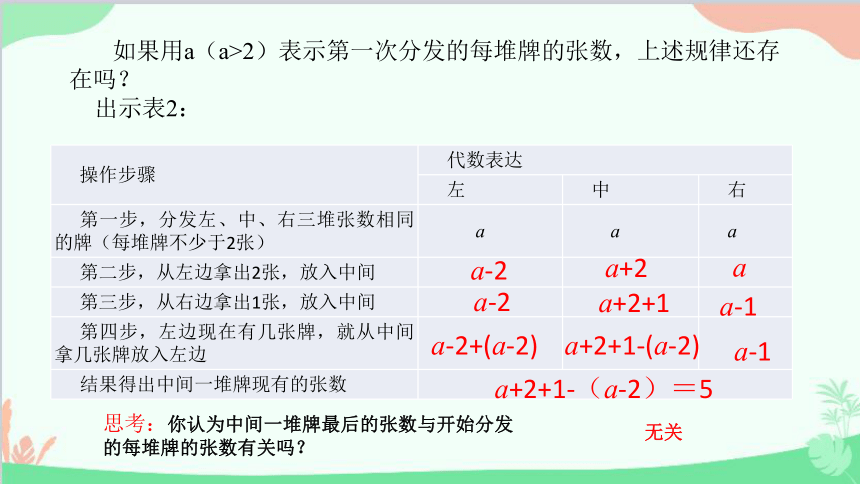
如果用a(a>2)表示第一次分发的每堆牌的张数,上述规律还存在吗?
出示表2:
a-2
a+2
a+2+1-(a-2)
a
a+2+1
a-2
a-1
a-2+(a-2)
a-1
a+2+1-(a-2)=5
思考:你认为中间一堆牌最后的张数与开始分发的每堆牌的张数有关吗?
无关
分析:如果心里想的数是78,根据规则得游戏结果是5×(7×2+3)+8=93;如果心里想的数是12,根据规则得游戏结果是5×(1×2+3)+2=27.可知93与78,27与12都相差15.
例 猜数游戏.
你在心里想好一个两位数,将十位数字乘2,然后加3,再将所得新数乘5,最后将得到的数加原来两位数的个位数字.把你的结果告诉我,我就知道你心里想的两位数.
(1)想好几个两位数,并按上述方法得到结果,比较它们之间的关系,你发现有什么规律?
(2)你能用语言描述你的发现吗?
(3)请用字母表达并借助代数式的运算解释其中的道理.
解:(1)游戏结果与心里想的两位数的差是15.
(2)把游戏结果减去15可得心里想的两位数.
(3)设心里想的两位数的十位数字为a,个位数字为b,则这个两位数可以表示为10a+b,则游戏结果为5(2a+3)+b=10a+15+b=(10a+b)+15.所以用计算结果减15,就得到心里想的两位数.
总结:
设计游戏,其实是一个逆向思维的过程,可以先设计好代数式及其化简结果,再赋予其背景.设计问题遵循“发现规律—表示规律—揭示规律”的过程,设计出题材丰富、形式新颖的游戏.如扑克牌发放游戏、寻找几何图形规律游戏等.体现了由特殊到一般,再由一般到特殊的过程.
随 堂 训 练
1.甲、乙两同学进行数字猜谜游戏:甲说一个数a的相反数就是它本身,乙说一个数b的倒数也等于它本身,请你猜一猜|a-b|= .
解析:相反数就是它本身的数是0;倒数等于它本身的数是1或-1.当a=0,b=1时,|a-b|=1;当a=0,b=-1时,|a-b|=1.总之|a-b|=1.
1
2.猜数游戏
请你随便想一个数,并将此数乘5加7,然后再将结果乘2减4,你将最后结果告诉我,我心里将这个结果减10,再除以10,我就能知道你想的数.你能用字母表达并借助代数式的运算解释其中的道理吗?
解:设心里想的数为a,根据游戏规则可得
{[(5a+7)×2-4]-10}÷10=(10a+14-4-10)÷10=10a÷10=a.
根据游戏规则最后得到的数与心里想的数相同.
3.田老师在数学课上带领同学们做数学游戏,规则如下:
根据游戏规则,回答下面的问题.
(1)若甲报的数为 ,则乙报的数为 ,丁报出的答案是 ;
(2)若甲报的数为-3,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是0,请写出甲报的数.
游戏规则
甲任报一个有理数传给乙;
乙把这个数减2后报给丙;
丙再把所得的数的绝对值报给丁;
丁再把这个数的一半减1,报出答案.
猜年龄
当你变成你父亲的年龄时,父亲多少岁了?只要你用现在父亲的年龄的2倍减去那时父亲的年龄,把结果告诉我,我就能知道你现在的年龄.请你用字母表达并借助代数式的运算解释其中的道理.
课后提升
解:设你现在的年龄为a岁,父亲现在的年龄为b岁.父亲和你的年龄相差(b-a)岁.假如你变成父亲的年龄b岁,则父亲的年龄变成b+(b-a)=(2b-a)(岁).根据题意,得2b-(2b-a)=2b-2b+a=a(岁).所得结果恰好是你现在的年龄 .所以只要你把结果告诉我,我就能知道你现在的年龄.
课 堂 小 结
数式变化中的规律
图形拼接中的规律
探索与
表达规律
探索 猜想 验证
特殊 一般
设计游戏,其实是一个逆向思维的过程,可以先设计好代数式及其化简结果,再赋予其背景.设计问题遵循“发现规律—表示规律—揭示规律”的过程.
谢谢大家!
第三章 整式及其加减
5 探究与表达规律
第三章 整式及其加减
第2课时 表达规律
1
2
会用代数式表达规律,能利用代数式的运算解释具体问题中蕴含的一般规律及现象.(重难点)
在解决问题的过程中体验归纳、分析、猜想、抽象、类比、转化等思维方法,发展抽象思维能力.(难点)
学 习 目 标
新 课 导 入
做一个游戏,游戏规则如下:
教师背对学生,学生按下列四个步骤操作:
第一步:分发左、中、右三堆张数相同的牌(每堆牌不少于2张);
第二步:从左边拿出2张,放入中间;
第三步:从右边拿出1张,放入中间;
第四步:左边现在有几张牌,就从中间拿几张牌放入左边.
只要你按照上述步骤做,我就能准确地说出中间一堆牌现有的张数.
知 识 讲 解
表达规律
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) 3 3 3
第二步,从左边拿出2张,放入中间 3-2 3+2 3
第三步,从右边拿出1张,放入中间 3-2 3+2+1 3-1
第四步,左边现在有几张牌,就从中间拿几张牌放入左边 3-2+(3-2) 3+2+1-(3-2) 3-1
结果得出中间一堆牌现有的张数 3+2+1-(3-2)=5
问题:前面的游戏中,中间一堆牌的最终结果有什么规律?
如表1
游戏中发现中间一堆牌的最终结果都是5张.
操作步骤 代数表达
左 中 右
第一步,分发左、中、右三堆张数相同的牌(每堆牌不少于2张) a a a
第二步,从左边拿出2张,放入中间
第三步,从右边拿出1张,放入中间
第四步,左边现在有几张牌,就从中间拿几张牌放入左边
结果得出中间一堆牌现有的张数
如果用a(a>2)表示第一次分发的每堆牌的张数,上述规律还存在吗?
出示表2:
a-2
a+2
a+2+1-(a-2)
a
a+2+1
a-2
a-1
a-2+(a-2)
a-1
a+2+1-(a-2)=5
思考:你认为中间一堆牌最后的张数与开始分发的每堆牌的张数有关吗?
无关
分析:如果心里想的数是78,根据规则得游戏结果是5×(7×2+3)+8=93;如果心里想的数是12,根据规则得游戏结果是5×(1×2+3)+2=27.可知93与78,27与12都相差15.
例 猜数游戏.
你在心里想好一个两位数,将十位数字乘2,然后加3,再将所得新数乘5,最后将得到的数加原来两位数的个位数字.把你的结果告诉我,我就知道你心里想的两位数.
(1)想好几个两位数,并按上述方法得到结果,比较它们之间的关系,你发现有什么规律?
(2)你能用语言描述你的发现吗?
(3)请用字母表达并借助代数式的运算解释其中的道理.
解:(1)游戏结果与心里想的两位数的差是15.
(2)把游戏结果减去15可得心里想的两位数.
(3)设心里想的两位数的十位数字为a,个位数字为b,则这个两位数可以表示为10a+b,则游戏结果为5(2a+3)+b=10a+15+b=(10a+b)+15.所以用计算结果减15,就得到心里想的两位数.
总结:
设计游戏,其实是一个逆向思维的过程,可以先设计好代数式及其化简结果,再赋予其背景.设计问题遵循“发现规律—表示规律—揭示规律”的过程,设计出题材丰富、形式新颖的游戏.如扑克牌发放游戏、寻找几何图形规律游戏等.体现了由特殊到一般,再由一般到特殊的过程.
随 堂 训 练
1.甲、乙两同学进行数字猜谜游戏:甲说一个数a的相反数就是它本身,乙说一个数b的倒数也等于它本身,请你猜一猜|a-b|= .
解析:相反数就是它本身的数是0;倒数等于它本身的数是1或-1.当a=0,b=1时,|a-b|=1;当a=0,b=-1时,|a-b|=1.总之|a-b|=1.
1
2.猜数游戏
请你随便想一个数,并将此数乘5加7,然后再将结果乘2减4,你将最后结果告诉我,我心里将这个结果减10,再除以10,我就能知道你想的数.你能用字母表达并借助代数式的运算解释其中的道理吗?
解:设心里想的数为a,根据游戏规则可得
{[(5a+7)×2-4]-10}÷10=(10a+14-4-10)÷10=10a÷10=a.
根据游戏规则最后得到的数与心里想的数相同.
3.田老师在数学课上带领同学们做数学游戏,规则如下:
根据游戏规则,回答下面的问题.
(1)若甲报的数为 ,则乙报的数为 ,丁报出的答案是 ;
(2)若甲报的数为-3,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是0,请写出甲报的数.
游戏规则
甲任报一个有理数传给乙;
乙把这个数减2后报给丙;
丙再把所得的数的绝对值报给丁;
丁再把这个数的一半减1,报出答案.
猜年龄
当你变成你父亲的年龄时,父亲多少岁了?只要你用现在父亲的年龄的2倍减去那时父亲的年龄,把结果告诉我,我就能知道你现在的年龄.请你用字母表达并借助代数式的运算解释其中的道理.
课后提升
解:设你现在的年龄为a岁,父亲现在的年龄为b岁.父亲和你的年龄相差(b-a)岁.假如你变成父亲的年龄b岁,则父亲的年龄变成b+(b-a)=(2b-a)(岁).根据题意,得2b-(2b-a)=2b-2b+a=a(岁).所得结果恰好是你现在的年龄 .所以只要你把结果告诉我,我就能知道你现在的年龄.
课 堂 小 结
数式变化中的规律
图形拼接中的规律
探索与
表达规律
探索 猜想 验证
特殊 一般
设计游戏,其实是一个逆向思维的过程,可以先设计好代数式及其化简结果,再赋予其背景.设计问题遵循“发现规律—表示规律—揭示规律”的过程.
谢谢大家!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
