4.6.2 角的比较和运算 课件(共25张PPT)
文档属性
| 名称 | 4.6.2 角的比较和运算 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 17:10:45 | ||
图片预览





文档简介
(共25张PPT)
4.6.2 角的比较和运算
华师大版 七年级上册
教学目标
【教学目标】
1.在现实情境中,运用类比的方法,学会比较两个角的大小,丰富对角的大小关系的认识,学会分析角的和差关系;
2.学会用三角板拼出不同度数的角,认识角的平分线及作一个角等于已知角;
3.进一步培养和提高学生的识图能力和动手操作能力,学会类比的数学思想.
【重点】比较角的大小、角的和差关系和角的平分线.
【难点】认识复杂图形中角的和差关系.
复习回顾
线段的比较方法
2. 从“形”出发,利用线段移动叠合的方法.
1. 以“数”出发,通过度量长度进行数值大小比较.量出其长度就可以直接比较大小.
A
C
A
B
C
A
A
B
A
B
(AB > AC)
(AB = AC)
(AB < AC)
A
C
新知探究
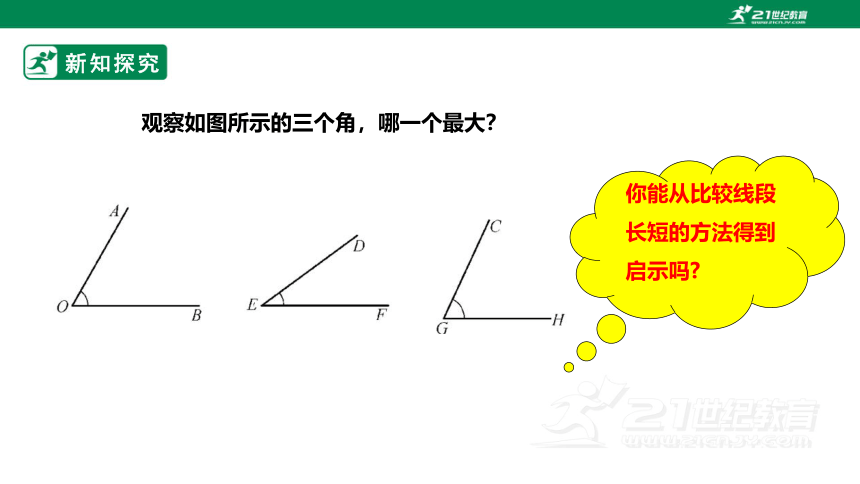
观察如图所示的三个角,哪一个最大?
你能从比较线段长短的方法得到启示吗
新知探究
从上图我们可以发现,∠DEF明显比∠AOB及∠CGH小,但∠AOB与∠CGH的大小关系不太明显.那么如何比较,才能得到准确的结果呢
新知探究
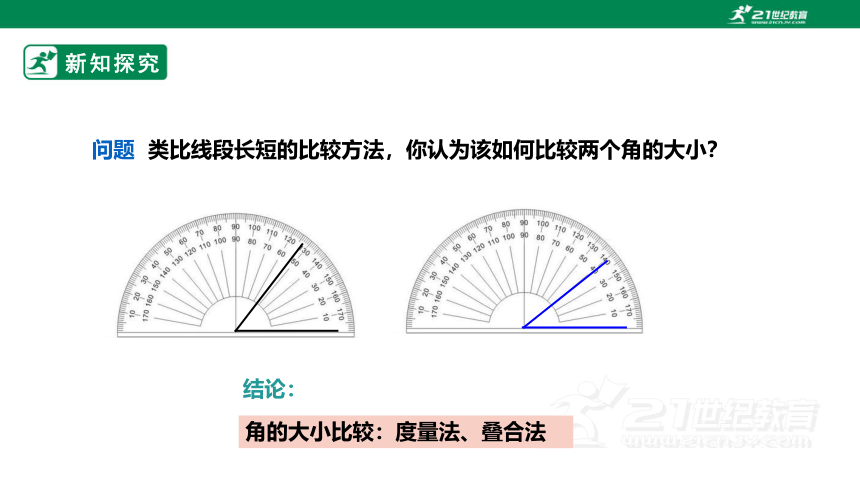
问题 类比线段长短的比较方法,你认为该如何比较两个角的大小?
结论:
角的大小比较:度量法、叠合法
新知探究
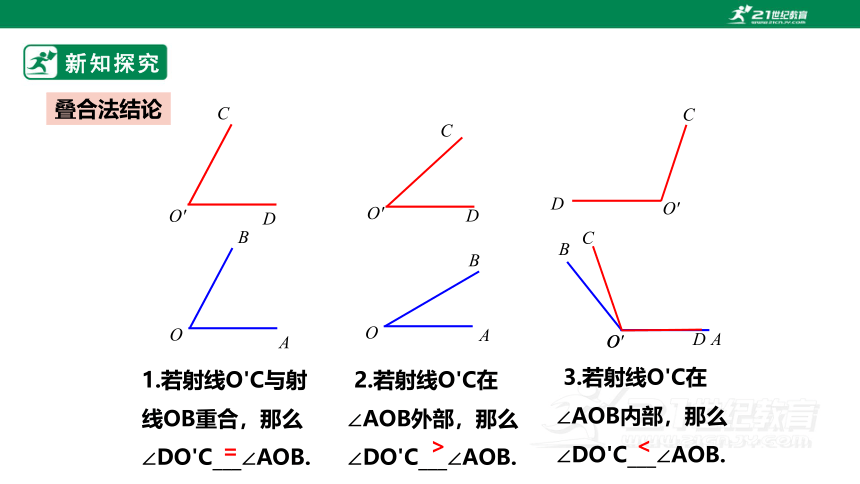
叠合法结论
O
B
A
O'
C
D
O
B
A
O'
C
D
O
B
A
O'
C
D
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那么∠DO'C___∠AOB.
3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.
=
>
<
O'
C
D
新知探究
一副三角尺上的角是一些常用的角,除了可以用它们直接画出30°、45°、60°和90°的角之外,还可以画出其他一些特殊的角.如图所示,用两种方法放置一副三角尺,可以画出75°和15°的角.
想一想 用一副三角尺还可以画出哪些特殊的角?
新知探究
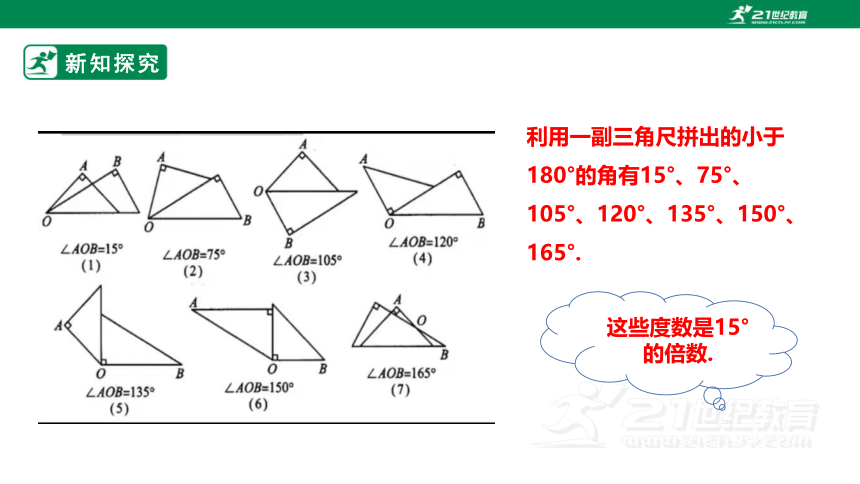
这些度数是15°的倍数.
利用一副三角尺拼出的小于180°的角有15°、75°、105°、120°、135°、150°、165°.
新知探究
如图,∠AOB为已知角,试按下列步骤用圆规和直尺准
确地画一个角等于∠AOB.
第一步:画射线O′A′;
第二步:以点O为圆心,以适当长为半径画弧,交OA于点C,交OB于点D;
第三步:以点O′为圆心,以OC长为半径画弧,交O′A′ 于点C′;
第四步:以点C′为圆心,以CD长为半径画弧,交前一条弧于点D ′;
第五步:经过点D′画射线O′B′. ∠ A′ O′B′ 就是所要画的角.
新知探究
我们可以对角进行简单的加减运算,如:
( 1 ) 34°34' + 21°51 ' = 55°85' = 56°25';
(2) 180° - 52°31' = 179°60' - 52°31' = 127°29'.
观察图中的∠AOC、∠COB和∠AOB,如何表示它们之间的关系呢
新知探究
我们可以用熟悉的“和差”来表示:
∠AOC+∠COB=∠AOB,或
∠AOB-∠AOC=∠COB,或
∠AOB-∠COB=∠AOC.
可见,两个角相加或相减,得到的和或差也是角.
新知探究
如图,用量角器和直尺在纸上画∠AOB =84°.然后沿点O对折,使边OB和OA重合,那么折痕把角分成了大小相等的两部分.
你也可以用量角器画出等分∠AOB的射线OC.
C
42°
42°
A
B
新知探究
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的角平分线,
所以∠AOC =∠BOC =∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
O
B
A
C
课堂练习
1.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
A.∠COD= ∠AOB B.∠AOD= ∠AOB
C.∠BOD= ∠AOD D.∠BOC= ∠AOD
D
课堂练习
2.计算90°-18°50'45″的结果正确的是 ( )
A.71°9'15″ B.72°9'15″
C.72°10'15″ D.71°10'15″
3.如图所示,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB
等于( )
A.50° B.75° C.100° D.120°
A
C
课堂练习
4.如图,OB是∠AOC的角平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
D
课堂练习
(2)如上图 :已知∠AOB = ∠BOC =∠COD,
则OB 是 的平分线;
∠AOC= ;∠BOC = = = .
A
B
C
O
5. (1)如下图,填空:
D
∠AOC+∠COD= ;
∠AOB+∠BOC= ;
∠BOD-∠COD= ;
∠AOD- =∠AOB
∠AOC
∠BOD
∠AOB
∠DOC
∠AOD
∠BOC
∠AOD
∠BOD
∠AOC
课堂练习
6. 如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=____.
7. 已知∠AOB=38°,∠BOC=25°,那么∠AOC的度是 .
34°
13°或63°
O
A
B
C
D
8. 20°30′×8;
9. 106°6′÷5.
解:原式 = (106÷5)°+(6÷5)′= 21°+1°÷5
+(6÷5)′= 21°+(66÷5)′=21°+13′+1′÷5
=21°+13′+60″÷5=21°13′12″
解:原式 = 20°×8+30′×8
= 160°240′
= 164°
课堂练习
10.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
课堂练习
(2) 若∠BOC=90°,求∠AOE的度数.
解:∵∠AOB=120°,
∠BOC=90°,
∴∠AOC=120°-90°
=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
课堂练习
课堂小结
角的比较
角的平分线
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
图形的关系
数量的关系
定义
几何符号语言表示
注意:几何图形角的和、差、倍、分的度数等于它们的度数的和、差、倍、分
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.6.2 角的比较和运算
华师大版 七年级上册
教学目标
【教学目标】
1.在现实情境中,运用类比的方法,学会比较两个角的大小,丰富对角的大小关系的认识,学会分析角的和差关系;
2.学会用三角板拼出不同度数的角,认识角的平分线及作一个角等于已知角;
3.进一步培养和提高学生的识图能力和动手操作能力,学会类比的数学思想.
【重点】比较角的大小、角的和差关系和角的平分线.
【难点】认识复杂图形中角的和差关系.
复习回顾
线段的比较方法
2. 从“形”出发,利用线段移动叠合的方法.
1. 以“数”出发,通过度量长度进行数值大小比较.量出其长度就可以直接比较大小.
A
C
A
B
C
A
A
B
A
B
(AB > AC)
(AB = AC)
(AB < AC)
A
C
新知探究
观察如图所示的三个角,哪一个最大?
你能从比较线段长短的方法得到启示吗
新知探究
从上图我们可以发现,∠DEF明显比∠AOB及∠CGH小,但∠AOB与∠CGH的大小关系不太明显.那么如何比较,才能得到准确的结果呢
新知探究
问题 类比线段长短的比较方法,你认为该如何比较两个角的大小?
结论:
角的大小比较:度量法、叠合法
新知探究
叠合法结论
O
B
A
O'
C
D
O
B
A
O'
C
D
O
B
A
O'
C
D
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那么∠DO'C___∠AOB.
3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.
=
>
<
O'
C
D
新知探究
一副三角尺上的角是一些常用的角,除了可以用它们直接画出30°、45°、60°和90°的角之外,还可以画出其他一些特殊的角.如图所示,用两种方法放置一副三角尺,可以画出75°和15°的角.
想一想 用一副三角尺还可以画出哪些特殊的角?
新知探究
这些度数是15°的倍数.
利用一副三角尺拼出的小于180°的角有15°、75°、105°、120°、135°、150°、165°.
新知探究
如图,∠AOB为已知角,试按下列步骤用圆规和直尺准
确地画一个角等于∠AOB.
第一步:画射线O′A′;
第二步:以点O为圆心,以适当长为半径画弧,交OA于点C,交OB于点D;
第三步:以点O′为圆心,以OC长为半径画弧,交O′A′ 于点C′;
第四步:以点C′为圆心,以CD长为半径画弧,交前一条弧于点D ′;
第五步:经过点D′画射线O′B′. ∠ A′ O′B′ 就是所要画的角.
新知探究
我们可以对角进行简单的加减运算,如:
( 1 ) 34°34' + 21°51 ' = 55°85' = 56°25';
(2) 180° - 52°31' = 179°60' - 52°31' = 127°29'.
观察图中的∠AOC、∠COB和∠AOB,如何表示它们之间的关系呢
新知探究
我们可以用熟悉的“和差”来表示:
∠AOC+∠COB=∠AOB,或
∠AOB-∠AOC=∠COB,或
∠AOB-∠COB=∠AOC.
可见,两个角相加或相减,得到的和或差也是角.
新知探究
如图,用量角器和直尺在纸上画∠AOB =84°.然后沿点O对折,使边OB和OA重合,那么折痕把角分成了大小相等的两部分.
你也可以用量角器画出等分∠AOB的射线OC.
C
42°
42°
A
B
新知探究
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的角平分线,
所以∠AOC =∠BOC =∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
O
B
A
C
课堂练习
1.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
A.∠COD= ∠AOB B.∠AOD= ∠AOB
C.∠BOD= ∠AOD D.∠BOC= ∠AOD
D
课堂练习
2.计算90°-18°50'45″的结果正确的是 ( )
A.71°9'15″ B.72°9'15″
C.72°10'15″ D.71°10'15″
3.如图所示,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB
等于( )
A.50° B.75° C.100° D.120°
A
C
课堂练习
4.如图,OB是∠AOC的角平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
D
课堂练习
(2)如上图 :已知∠AOB = ∠BOC =∠COD,
则OB 是 的平分线;
∠AOC= ;∠BOC = = = .
A
B
C
O
5. (1)如下图,填空:
D
∠AOC+∠COD= ;
∠AOB+∠BOC= ;
∠BOD-∠COD= ;
∠AOD- =∠AOB
∠AOC
∠BOD
∠AOB
∠DOC
∠AOD
∠BOC
∠AOD
∠BOD
∠AOC
课堂练习
6. 如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=____.
7. 已知∠AOB=38°,∠BOC=25°,那么∠AOC的度是 .
34°
13°或63°
O
A
B
C
D
8. 20°30′×8;
9. 106°6′÷5.
解:原式 = (106÷5)°+(6÷5)′= 21°+1°÷5
+(6÷5)′= 21°+(66÷5)′=21°+13′+1′÷5
=21°+13′+60″÷5=21°13′12″
解:原式 = 20°×8+30′×8
= 160°240′
= 164°
课堂练习
10.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
课堂练习
(2) 若∠BOC=90°,求∠AOE的度数.
解:∵∠AOB=120°,
∠BOC=90°,
∴∠AOC=120°-90°
=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
课堂练习
课堂小结
角的比较
角的平分线
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
图形的关系
数量的关系
定义
几何符号语言表示
注意:几何图形角的和、差、倍、分的度数等于它们的度数的和、差、倍、分
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
