3.2.2双曲线的简单几何性质(第一课时) 课件(共18张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质(第一课时) 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 16:52:53 | ||
图片预览




文档简介
(共18张PPT)
第三章
圆锥曲线方程
3.2.2
双曲线的简单几何性质
(第一课时)
复习引入
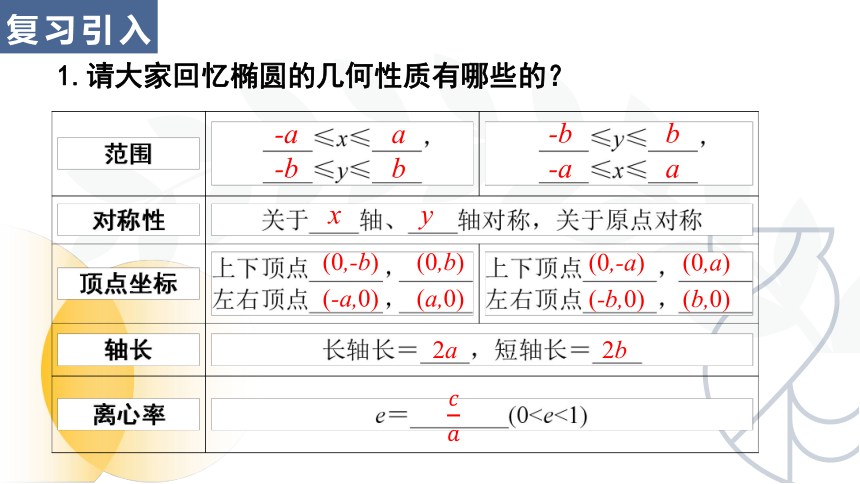
1.请大家回忆椭圆的几何性质有哪些的?
-a a
-b b
-a a
-b b
x y
(-a,0) (a,0)
(0,-b) (0,b)
(-b,0) (b,0)
(0,-a) (0,a)
2a 2b
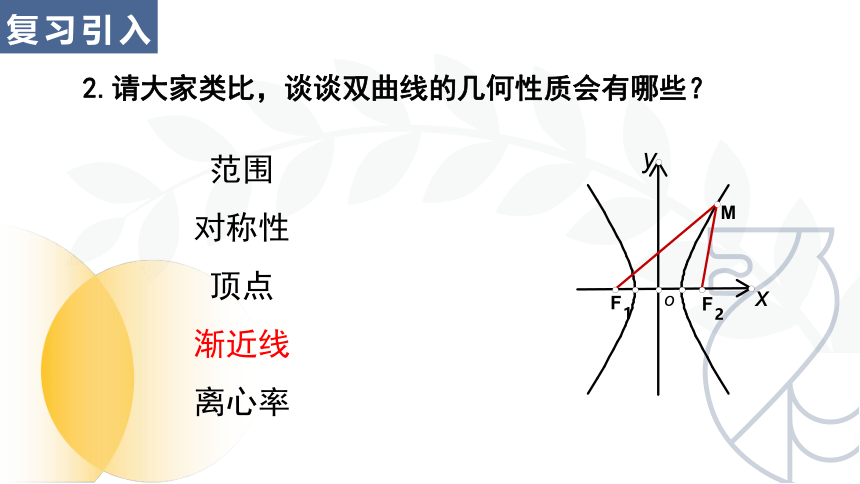
2.请大家类比,谈谈双曲线的几何性质会有哪些?
复习引入
范围
对称性
顶点
渐近线
离心率
x
y
o
F1
F2
一、范围
研究双曲线 的简单几何性质
对称轴:x轴、y轴
对称中心:原点(0,0),又叫做双曲线的中心.
课堂探究
,即
,
二、对称性
x
y
o
-b
b
-a
a
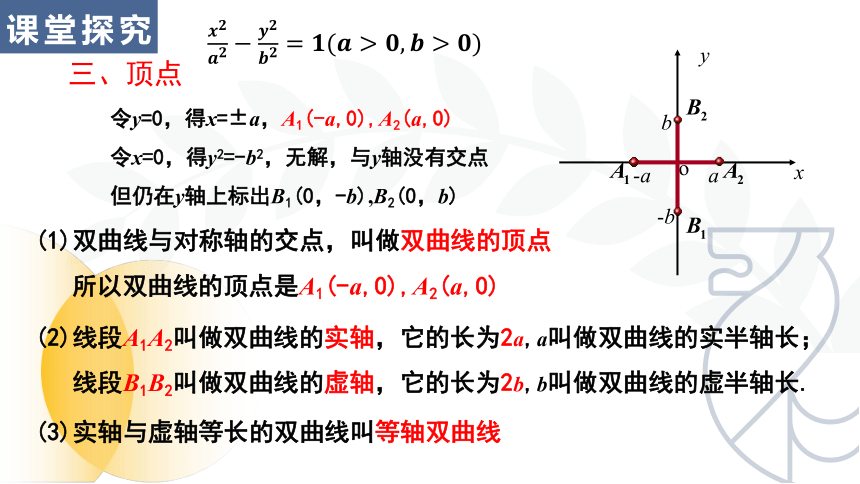
令y=0,得x=±a,A1(-a,0),A2(a,0)
令x=0,得y2=-b2,无解,与y轴没有交点
但仍在y轴上标出B1(0,-b),B2(0,b)
(1)双曲线与对称轴的交点,叫做双曲线的顶点
所以双曲线的顶点是A1(-a,0),A2(a,0)
(2)线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
(3)实轴与虚轴等长的双曲线叫等轴双曲线
课堂探究
三、顶点
课堂探究
四、离心率
(1)定义:双曲线的焦距与实轴长的比,叫做双曲线的离心率
(2)的范围:
e 是表示双曲线开口大小的一个量,e 越大开口越大
(3)尝试用a,b表示双曲线的离心率
【解析】:
(2)利用渐近线可以较准确的画出双曲线的草图
(3)渐近线对双曲线的开口的影响
课堂探究
五、渐近线
(1)双曲线 的渐近线为
注意:等轴双曲线的渐近线为
辨析:双曲线与椭圆的不同点
课堂探究
(1)曲线支数:双曲线是2支曲线,椭圆是1条封闭曲线.
(2)顶点个数:双曲线有2个顶点,椭圆有4个顶点.
(3)双曲线有实轴、虚轴,椭圆有长轴、短轴.
(4)渐近线:双曲线两条渐近线是特有的.
(5)离心率:双曲线离心率e∈(1,+∞),椭圆离心率e∈(0,1).
(6)双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的等量关系有区别.
例1:求下列双曲线的实轴和虚轴的长、顶点和焦点坐标及离心率,渐近线。
(1)
(2)
(3)
(4)
例题解析
例题解析
例2:求下列双曲线的实轴和虚轴的长、顶点和焦点坐标及离心率,渐近线。
(1) 实轴长为8,离心率为;
(2) 双曲线的实轴长和虚轴长相等,且过点P(4,-)
(3) 渐近线方程为,且经过点A(2,-)
例2:(1) 实轴长为8,离心率为;
例题解析
【解析】(1) 设双曲线的标准方程为 或
,
由题意知,
或
例2:(2) 双曲线的实轴长和虚轴长相等,且过点P(4,-)
例题解析
【解析】(2) 由
可设双曲线方程为
双曲线过P(4,-),,即
双曲线方程为
。
例2:(3) 渐近线方程为,且经过点A(2,-)
例题解析
【解析】(3) 方法一: 双曲线的渐近线方程为,
若焦点在x轴上,设双曲线标准方程为 ,
则 ① 在双曲线上, ②
联立①②,无解
若焦点在x轴上,设双曲线标准方程为 ,
则 ③ 在双曲线上, ④
联立③④,解得
双曲线标准方程为。
例2:(3) 渐近线方程为,且经过点A(2,-)
例题解析
【解析】(3) 方法二: 双曲线的渐近线方程为,
设双曲线标准方程为 ,
在双曲线上,
即
双曲线标准方程为。
练习巩固
1、已知双曲线的标准方程为 的左右焦点分别为F1、F2,点P为双曲线上一点,且,则双曲线的离心率为( )
【解析】如图所示,在△PF1F2中,,
所以,
根据双曲线的定义
有,
故离心率
练习巩固
2、双曲线 的两条渐近线互相垂直,那么该双曲线的离心率为( )
A.2 B. C. D.
C
【解析】由题意得,,所以
则,所以
课堂小结
总结:你学到了什么?
1、双曲线的性质:
范围、顶点、对称性、渐近线、离心率
2、求解双曲线的性质问题
作业1:
作业2:
作业3:
作业布置
第三章
圆锥曲线方程
3.2.2
双曲线的简单几何性质
(第一课时)
复习引入
1.请大家回忆椭圆的几何性质有哪些的?
-a a
-b b
-a a
-b b
x y
(-a,0) (a,0)
(0,-b) (0,b)
(-b,0) (b,0)
(0,-a) (0,a)
2a 2b
2.请大家类比,谈谈双曲线的几何性质会有哪些?
复习引入
范围
对称性
顶点
渐近线
离心率
x
y
o
F1
F2
一、范围
研究双曲线 的简单几何性质
对称轴:x轴、y轴
对称中心:原点(0,0),又叫做双曲线的中心.
课堂探究
,即
,
二、对称性
x
y
o
-b
b
-a
a
令y=0,得x=±a,A1(-a,0),A2(a,0)
令x=0,得y2=-b2,无解,与y轴没有交点
但仍在y轴上标出B1(0,-b),B2(0,b)
(1)双曲线与对称轴的交点,叫做双曲线的顶点
所以双曲线的顶点是A1(-a,0),A2(a,0)
(2)线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
(3)实轴与虚轴等长的双曲线叫等轴双曲线
课堂探究
三、顶点
课堂探究
四、离心率
(1)定义:双曲线的焦距与实轴长的比,叫做双曲线的离心率
(2)的范围:
e 是表示双曲线开口大小的一个量,e 越大开口越大
(3)尝试用a,b表示双曲线的离心率
【解析】:
(2)利用渐近线可以较准确的画出双曲线的草图
(3)渐近线对双曲线的开口的影响
课堂探究
五、渐近线
(1)双曲线 的渐近线为
注意:等轴双曲线的渐近线为
辨析:双曲线与椭圆的不同点
课堂探究
(1)曲线支数:双曲线是2支曲线,椭圆是1条封闭曲线.
(2)顶点个数:双曲线有2个顶点,椭圆有4个顶点.
(3)双曲线有实轴、虚轴,椭圆有长轴、短轴.
(4)渐近线:双曲线两条渐近线是特有的.
(5)离心率:双曲线离心率e∈(1,+∞),椭圆离心率e∈(0,1).
(6)双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的等量关系有区别.
例1:求下列双曲线的实轴和虚轴的长、顶点和焦点坐标及离心率,渐近线。
(1)
(2)
(3)
(4)
例题解析
例题解析
例2:求下列双曲线的实轴和虚轴的长、顶点和焦点坐标及离心率,渐近线。
(1) 实轴长为8,离心率为;
(2) 双曲线的实轴长和虚轴长相等,且过点P(4,-)
(3) 渐近线方程为,且经过点A(2,-)
例2:(1) 实轴长为8,离心率为;
例题解析
【解析】(1) 设双曲线的标准方程为 或
,
由题意知,
或
例2:(2) 双曲线的实轴长和虚轴长相等,且过点P(4,-)
例题解析
【解析】(2) 由
可设双曲线方程为
双曲线过P(4,-),,即
双曲线方程为
。
例2:(3) 渐近线方程为,且经过点A(2,-)
例题解析
【解析】(3) 方法一: 双曲线的渐近线方程为,
若焦点在x轴上,设双曲线标准方程为 ,
则 ① 在双曲线上, ②
联立①②,无解
若焦点在x轴上,设双曲线标准方程为 ,
则 ③ 在双曲线上, ④
联立③④,解得
双曲线标准方程为。
例2:(3) 渐近线方程为,且经过点A(2,-)
例题解析
【解析】(3) 方法二: 双曲线的渐近线方程为,
设双曲线标准方程为 ,
在双曲线上,
即
双曲线标准方程为。
练习巩固
1、已知双曲线的标准方程为 的左右焦点分别为F1、F2,点P为双曲线上一点,且,则双曲线的离心率为( )
【解析】如图所示,在△PF1F2中,,
所以,
根据双曲线的定义
有,
故离心率
练习巩固
2、双曲线 的两条渐近线互相垂直,那么该双曲线的离心率为( )
A.2 B. C. D.
C
【解析】由题意得,,所以
则,所以
课堂小结
总结:你学到了什么?
1、双曲线的性质:
范围、顶点、对称性、渐近线、离心率
2、求解双曲线的性质问题
作业1:
作业2:
作业3:
作业布置
