1.4.2 用空间向量研究距离、夹角问题(第三课时) 课件(共26张PPT)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题(第三课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 16:53:46 | ||
图片预览






文档简介
(共26张PPT)
1.4.2用空间向量研究距离、夹角问题
第三课时
1.理解异面直线所成角、直线与平面所成角、二面角与空间向量之间的关系,并会用向量方法求简单夹角问题.
2.能描述用空间向量解决立体几何问题的程序,体会向量方法在研究几何问题中的作用.
学习目标
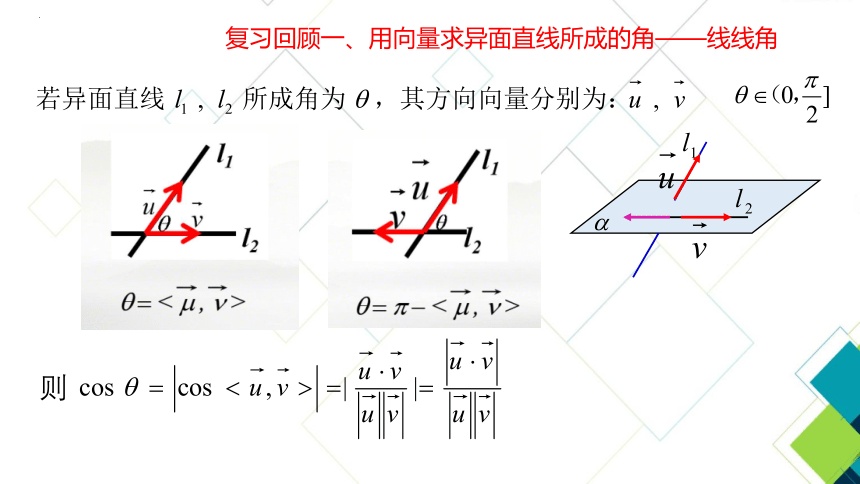
复习回顾一、用向量求异面直线所成的角——线线角
则
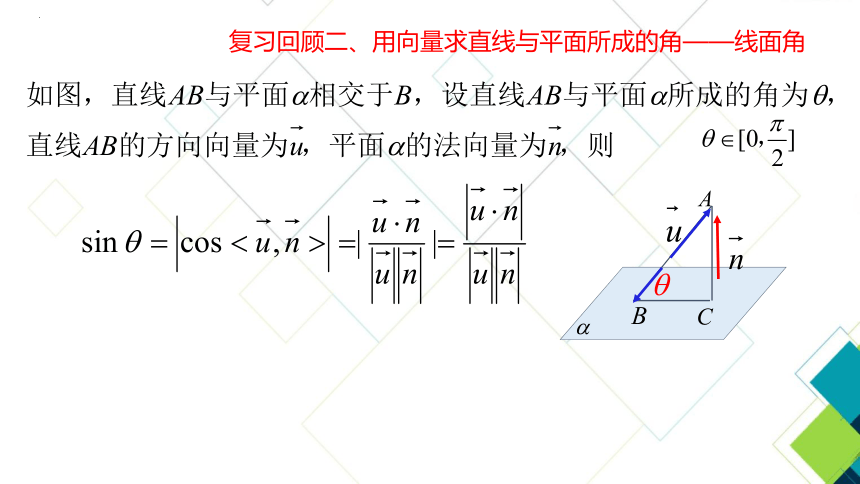
复习回顾二、用向量求直线与平面所成的角——线面角
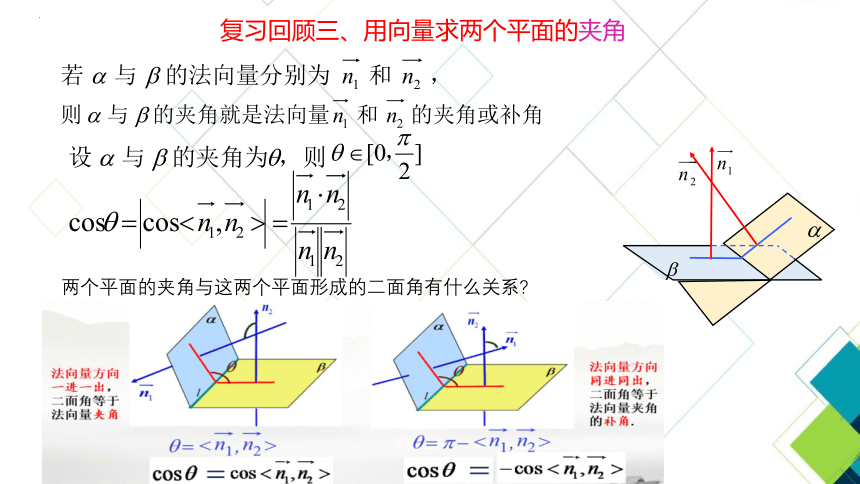
复习回顾三、用向量求两个平面的夹角
两个平面的夹角与这两个平面形成的二面角有什么关系
例9、如图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°.已知礼物的质量为1kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8m/s ,精确到 0.01N).
分析:因为降落伞匀速下落,所以降落伞8根绳子拉力的合力的大小等于礼物重力的大小.8根绳子的拉力在水平面的法向量方向上的投影向量的和向量与礼物的重力是一对相反向量.
用空间向量解决实际问题,综合问题
解:
A
B
D
P
E
F
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
(2)求证:PB⊥平面EFD;
(3)求平面CPB与平面PBD的夹角的大小。
分析:本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角。这些问题都可以利用向量方法解决。由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标示系,用向量及坐标表示问题中的几何元素,进而解决问题。
例10
A
B
D
P
E
F
G
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
向量法
A
B
D
P
E
F
G
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD;
A
B
D
P
E
F
G
C
(3)求平面CPB与平面PBD的夹角的大小。
A
B
C
D
P
E
F
X
Y
Z
平面PBC的一个法向量为
(3)解法二:如图所示建立空间直角坐标系D-xyz.
平面PBD的一个法向量为
G
(3)求平面CPB与平面PBD的夹角的大小。
(3)解法三:用待定系数法求出平面PBC的一个法向量与平面PBD的一个法向量。
A
B
D
P
E
F
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
几何法
O
几何法
(2)求证:PB⊥平面EFD;
A
B
C
D
P
E
F
几何法
(3)求平面CPB与平面PBD的夹角的大小。
.
用向量解决立体几何问题的方法
解决立体几何中的问题,可用三种方法:
(1)综合法:以逻辑推理作为工具解决问题;
(2)向量法:利用向量的概念及其运算解决问题;
(3)坐标法:利用数及其运算来解决问题
练习
课本P41
练习1:如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,
E,F分别是BC,A1D1的中点.
(1)求直线A1C与DE所成角的余弦值;
解 以A为坐标原点,分别以AB,AD,AA1所在直线
为x轴,y轴,z轴,建立空间直角坐标系Axyz.
(2)求直线AD与平面B1EDF所成角的余弦值;
解 连接DB1,∵∠ADE=∠ADF,
∴AD在平面B1EDF内的射影在∠EDF的平分线上.
又四边形B1EDF为菱形,∴DB1为∠EDF的平分线,
故直线AD与平面B1EDF所成的角为∠ADB1.
由A(0,0,0),B1(a,0,a),D(0,a,0),
(3)求平面B1EDF与平面ABCD夹角的余弦值.
设平面B1EDF的一个法向量为n=(1,y,z),
解:(1) 有题意可知 面
又 面 ,所以面 面
【走进高考】(2018全国一卷)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把 折起,使点C到达点P的位置,且 .
(1)证明:平面PEF⊥平面ABFD.
(2)求DP与平面ABFD所成角的正弦值.
(2)过点P作 ,有(1)知PH 面ABFD
现以H为坐标原点,建立如图所示的坐标系.
,所以 .
设正方形ABCD的边长为2,
则 ,
因此 .由此可知 ,
则可得:
若设DP与面ABFD所成角为 ,则 .
察天下事
读圣贤书
成栋梁才
1.4.2用空间向量研究距离、夹角问题
第三课时
1.理解异面直线所成角、直线与平面所成角、二面角与空间向量之间的关系,并会用向量方法求简单夹角问题.
2.能描述用空间向量解决立体几何问题的程序,体会向量方法在研究几何问题中的作用.
学习目标
复习回顾一、用向量求异面直线所成的角——线线角
则
复习回顾二、用向量求直线与平面所成的角——线面角
复习回顾三、用向量求两个平面的夹角
两个平面的夹角与这两个平面形成的二面角有什么关系
例9、如图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°.已知礼物的质量为1kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8m/s ,精确到 0.01N).
分析:因为降落伞匀速下落,所以降落伞8根绳子拉力的合力的大小等于礼物重力的大小.8根绳子的拉力在水平面的法向量方向上的投影向量的和向量与礼物的重力是一对相反向量.
用空间向量解决实际问题,综合问题
解:
A
B
D
P
E
F
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
(2)求证:PB⊥平面EFD;
(3)求平面CPB与平面PBD的夹角的大小。
分析:本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角。这些问题都可以利用向量方法解决。由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标示系,用向量及坐标表示问题中的几何元素,进而解决问题。
例10
A
B
D
P
E
F
G
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
向量法
A
B
D
P
E
F
G
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD;
A
B
D
P
E
F
G
C
(3)求平面CPB与平面PBD的夹角的大小。
A
B
C
D
P
E
F
X
Y
Z
平面PBC的一个法向量为
(3)解法二:如图所示建立空间直角坐标系D-xyz.
平面PBD的一个法向量为
G
(3)求平面CPB与平面PBD的夹角的大小。
(3)解法三:用待定系数法求出平面PBC的一个法向量与平面PBD的一个法向量。
A
B
D
P
E
F
C
例10、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
几何法
O
几何法
(2)求证:PB⊥平面EFD;
A
B
C
D
P
E
F
几何法
(3)求平面CPB与平面PBD的夹角的大小。
.
用向量解决立体几何问题的方法
解决立体几何中的问题,可用三种方法:
(1)综合法:以逻辑推理作为工具解决问题;
(2)向量法:利用向量的概念及其运算解决问题;
(3)坐标法:利用数及其运算来解决问题
练习
课本P41
练习1:如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,
E,F分别是BC,A1D1的中点.
(1)求直线A1C与DE所成角的余弦值;
解 以A为坐标原点,分别以AB,AD,AA1所在直线
为x轴,y轴,z轴,建立空间直角坐标系Axyz.
(2)求直线AD与平面B1EDF所成角的余弦值;
解 连接DB1,∵∠ADE=∠ADF,
∴AD在平面B1EDF内的射影在∠EDF的平分线上.
又四边形B1EDF为菱形,∴DB1为∠EDF的平分线,
故直线AD与平面B1EDF所成的角为∠ADB1.
由A(0,0,0),B1(a,0,a),D(0,a,0),
(3)求平面B1EDF与平面ABCD夹角的余弦值.
设平面B1EDF的一个法向量为n=(1,y,z),
解:(1) 有题意可知 面
又 面 ,所以面 面
【走进高考】(2018全国一卷)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把 折起,使点C到达点P的位置,且 .
(1)证明:平面PEF⊥平面ABFD.
(2)求DP与平面ABFD所成角的正弦值.
(2)过点P作 ,有(1)知PH 面ABFD
现以H为坐标原点,建立如图所示的坐标系.
,所以 .
设正方形ABCD的边长为2,
则 ,
因此 .由此可知 ,
则可得:
若设DP与面ABFD所成角为 ,则 .
察天下事
读圣贤书
成栋梁才
