1.4.2 用空间向量研究距离、夹角问题(第二课时) 课件(共21张PPT)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题(第二课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 16:54:16 | ||
图片预览






文档简介
(共21张PPT)
1.4.2 用空间向量研究距离、
夹角问题
第2课时 用空间向量研究夹角问题
学 习 任 务 核 心 素 养
1.能用向量语言表述线线、线面、平面与平面的夹角.(重点、易混点) 2.能用向量方法解决线线、线面、平面与平面的夹角问题.(重点、难点) 3.能描述用向量方法解决夹角问题的程序,体会向量方法在研究几何问题中的作用. 1.通过学习线线、线面、平面与平面的向量表示,提升直观想象素养.
2.通过利用向量方法解决线线、线面、平面与平面的夹角问题,提升逻辑推理和数学运算素养.
与距离类似,角度是立体几何中另一个重要的度量.我们能否用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角?
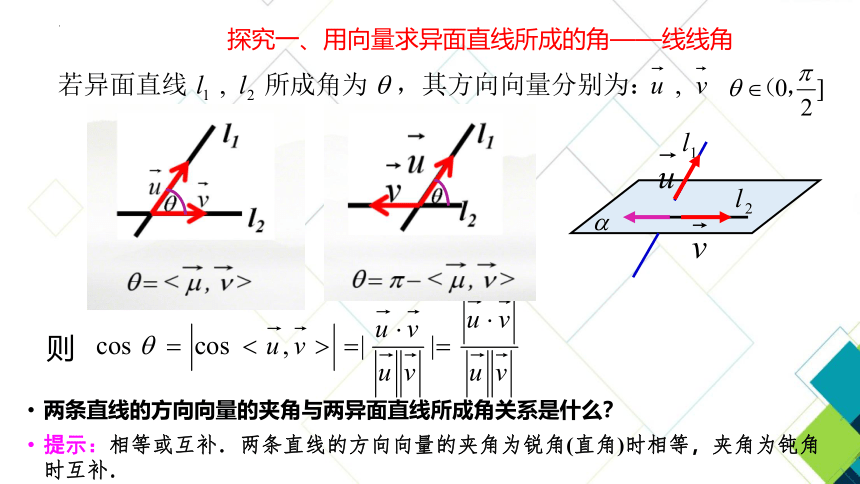
探究一、用向量求异面直线所成的角——线线角
则
两条直线的方向向量的夹角与两异面直线所成角关系是什么?
提示:相等或互补.两条直线的方向向量的夹角为锐角(直角)时相等,夹角为钝角时互补.
思考:以上我们用向量解决了异面直线 AM 和 CN 所成角的问题,你能用向量方法求直线 AB 和平面 BCD 所成的角吗?
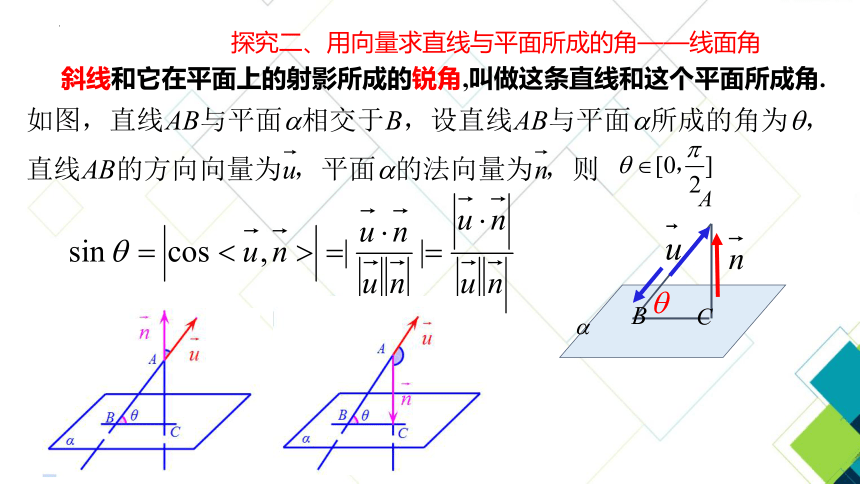
类似地,直线与平面所成的角,可以转化为直线的方向向量和平面的法向量的夹角
探究二、用向量求直线与平面所成的角——线面角
斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成角.
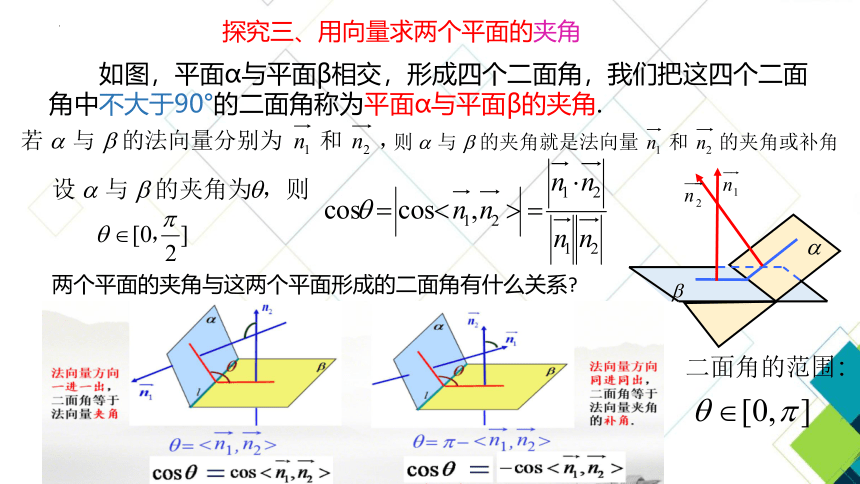
探究三、用向量求两个平面的夹角
两个平面的夹角与这两个平面形成的二面角有什么关系
如图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
二面角的范围:
一、用向量求异面直线所成的角
二、用向量求直线与平面角
三、用向量求两个平面的夹角
总结:
解:①化为向量问题
例1、如图,在棱长为1的正四面体(四个面都是正三角形) ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
②进行向量运算
③回到图形问题
(1)几何法
解决此类问题,关键是通过平移求解.过某一点作平行线,将异面直线所成的角转化为平面角,最后通过解三角形求解.主要以“作,证,算”来求异面直线所成的角,同时,要注意异面直线所成角的范围.
(2)向量法
利用数量积或坐标方法将异面直线所成的角θ 转化为两直线的方向向量所成的角 ,若求出的两向量的夹角为钝角,则异面直线的夹角应为两向量夹角的补角,即 .
求异面直线所成的角的两种方法
课本P38
2.PA,PB,PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线 PC 与平面 PAB 所成角的的余弦值是( ).
例2、PA,PB,PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线 PC 与平面 PAB 所成角的的余弦值是( ).
C
(1)几何法
找直线在平面内的射影,充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值).
(2)向量法
①建立空间直角坐标系;
②求直线的方向向量 ;
③求平面的法向量 ;
④计算:设线面角为θ,则 .
求直线与平面的夹角的方法与步骤
解:①化为向量问题
分析:因为平面 PQR 与平西面A1B1C1的夹角可以转化为平面 PQR 与平面A1B1C1的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
例3、如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1,求平面PQR与平面A1B1C1夹角的余弦值.
②进行向量运算
③回到图形问题
(1)几何法
在二面角的棱上找一特殊点,在两个半平面内分别作垂直于棱的射线,把平面角放到三角形中求解.
(2)向量法
①建立空间直角坐标系;
②求出两个半平面的法向量 , ;
③设二面角的平面角为θ,则 ;
④根据图形判断 θ 为钝角还是锐角,从而求出θ(或其三角函数).
求平面与平面的夹角的方法与步骤
1、在直三棱柱 ABC-A1B1C1中,∠BCA=90°,D1,F1分别是A1B1,A1C1的中点,BC= CA=CC1,则BD1与AF1所成角的余弦值是( )
A. B. C. D.
A
课本P38
3: 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,求平面AA1B与平面A1BC1夹角的余弦值.
A
B
C
A1
B1
C1
O
y
z
D
x
4、如图,ABC和DBC所在平面垂直,且AB=BC=BD. ∠DBC=.
(1) 直线AD与直线BC所成角的大小;
(2)直线AD与平面BCD 所成角的大
(3)平面ABD和平面BDC 的夹角的余弦值.
A
B
C
D
x
y
z
察天下事
读圣贤书
成栋梁才
1.4.2 用空间向量研究距离、
夹角问题
第2课时 用空间向量研究夹角问题
学 习 任 务 核 心 素 养
1.能用向量语言表述线线、线面、平面与平面的夹角.(重点、易混点) 2.能用向量方法解决线线、线面、平面与平面的夹角问题.(重点、难点) 3.能描述用向量方法解决夹角问题的程序,体会向量方法在研究几何问题中的作用. 1.通过学习线线、线面、平面与平面的向量表示,提升直观想象素养.
2.通过利用向量方法解决线线、线面、平面与平面的夹角问题,提升逻辑推理和数学运算素养.
与距离类似,角度是立体几何中另一个重要的度量.我们能否用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角?
探究一、用向量求异面直线所成的角——线线角
则
两条直线的方向向量的夹角与两异面直线所成角关系是什么?
提示:相等或互补.两条直线的方向向量的夹角为锐角(直角)时相等,夹角为钝角时互补.
思考:以上我们用向量解决了异面直线 AM 和 CN 所成角的问题,你能用向量方法求直线 AB 和平面 BCD 所成的角吗?
类似地,直线与平面所成的角,可以转化为直线的方向向量和平面的法向量的夹角
探究二、用向量求直线与平面所成的角——线面角
斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成角.
探究三、用向量求两个平面的夹角
两个平面的夹角与这两个平面形成的二面角有什么关系
如图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
二面角的范围:
一、用向量求异面直线所成的角
二、用向量求直线与平面角
三、用向量求两个平面的夹角
总结:
解:①化为向量问题
例1、如图,在棱长为1的正四面体(四个面都是正三角形) ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
②进行向量运算
③回到图形问题
(1)几何法
解决此类问题,关键是通过平移求解.过某一点作平行线,将异面直线所成的角转化为平面角,最后通过解三角形求解.主要以“作,证,算”来求异面直线所成的角,同时,要注意异面直线所成角的范围.
(2)向量法
利用数量积或坐标方法将异面直线所成的角θ 转化为两直线的方向向量所成的角 ,若求出的两向量的夹角为钝角,则异面直线的夹角应为两向量夹角的补角,即 .
求异面直线所成的角的两种方法
课本P38
2.PA,PB,PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线 PC 与平面 PAB 所成角的的余弦值是( ).
例2、PA,PB,PC是从点P出发的三条射线,每两条射线的夹角均为60°,那么直线 PC 与平面 PAB 所成角的的余弦值是( ).
C
(1)几何法
找直线在平面内的射影,充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值).
(2)向量法
①建立空间直角坐标系;
②求直线的方向向量 ;
③求平面的法向量 ;
④计算:设线面角为θ,则 .
求直线与平面的夹角的方法与步骤
解:①化为向量问题
分析:因为平面 PQR 与平西面A1B1C1的夹角可以转化为平面 PQR 与平面A1B1C1的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
例3、如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1,求平面PQR与平面A1B1C1夹角的余弦值.
②进行向量运算
③回到图形问题
(1)几何法
在二面角的棱上找一特殊点,在两个半平面内分别作垂直于棱的射线,把平面角放到三角形中求解.
(2)向量法
①建立空间直角坐标系;
②求出两个半平面的法向量 , ;
③设二面角的平面角为θ,则 ;
④根据图形判断 θ 为钝角还是锐角,从而求出θ(或其三角函数).
求平面与平面的夹角的方法与步骤
1、在直三棱柱 ABC-A1B1C1中,∠BCA=90°,D1,F1分别是A1B1,A1C1的中点,BC= CA=CC1,则BD1与AF1所成角的余弦值是( )
A. B. C. D.
A
课本P38
3: 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,求平面AA1B与平面A1BC1夹角的余弦值.
A
B
C
A1
B1
C1
O
y
z
D
x
4、如图,ABC和DBC所在平面垂直,且AB=BC=BD. ∠DBC=.
(1) 直线AD与直线BC所成角的大小;
(2)直线AD与平面BCD 所成角的大
(3)平面ABD和平面BDC 的夹角的余弦值.
A
B
C
D
x
y
z
察天下事
读圣贤书
成栋梁才
