数学人教A版(2019)必修第一册5.3 诱导公式 课件(共44张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.3 诱导公式 课件(共44张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 00:00:00 | ||
图片预览








文档简介
(共44张PPT)
5.3 诱导公式
第五章 三角函数
引 入
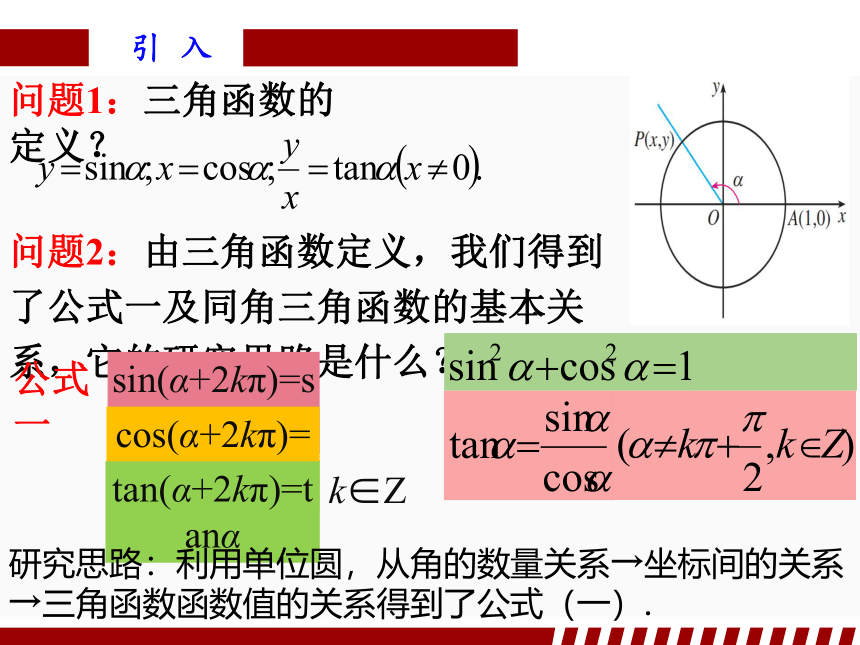
问题1:三角函数的定义?
问题2:由三角函数定义,我们得到了公式一及同角三角函数的基本关系,它的研究思路是什么?
sin(α+2kπ)=sinα
cos(α+2kπ)=cosα
tan(α+2kπ)=tanα
公式一
k∈Z
研究思路:利用单位圆,从角的数量关系→坐标间的关系→三角函数函数值的关系得到了公式(一).
引 入
α∈(0°,90°)
180°+α∈(180°,270°)
180°-α∈(90°,180°)
360°-α∈(270°,360°)
问题3:能否再把0°~ 360°间的角的三角函数求值,化为我们熟悉的00~900间的角的三角函数求值问题呢?
圆的最重要的性质是对称性,而对称性(如奇偶性)也是函数的重要性质.由此想到,可以利用圆的对称性,研究三角函数的对称性.
探究新知
P1(x1,y1)
O
x
α
y
P4(x4,y4)
P1(x1,y1)
O
x
α
y
P3(x3,y3)
问题4:(1)作P1关于原点的对称点P2,以OP2为终边的角β与角α有什么关系?角β,α的三角函数值之间有什么关系?
(2)作P1关于x轴的对称点P3,有什么结论?
(3)作P1关于y轴的对称点P4,有什么结论?
180°+α∈(180°,270°)
P1(x1,y1)
O
x
α
y
P2(x2,y2)
360°-α∈(270°,360°)
-α
180°-α∈(90°,180°)
探究新知
P1(x,y)
O
x
α
y
P2(-x,-y)
π+α
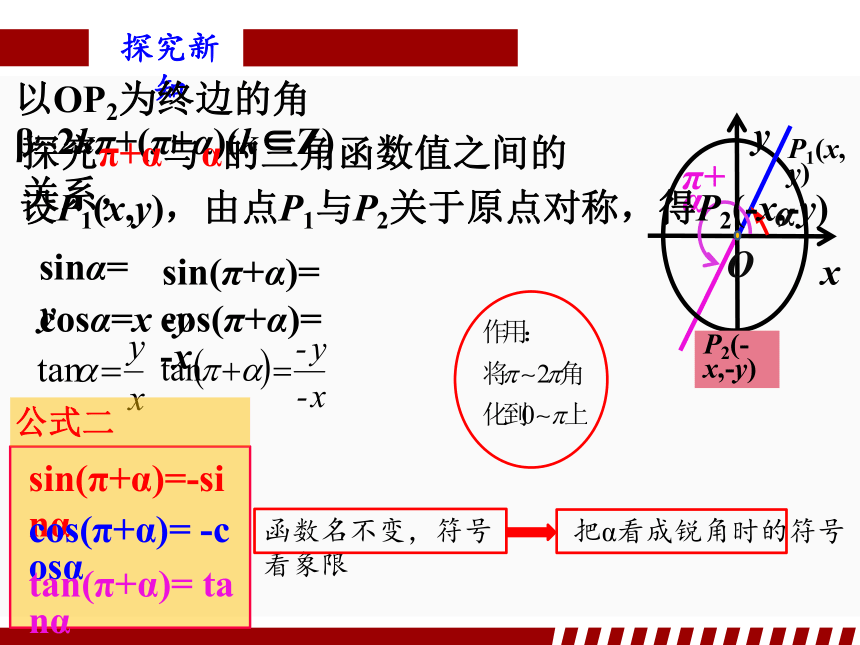
以OP2为终边的角β=2kπ+(π+α)(k∈Z)
sinα=y
cosα=x
探究π+α与α的三角函数值之间的关系,
sin(π+α)= -y
cos(π+α)= -x
sin(π+α)=-sinα
cos(π+α)= -cosα
tan(π+α)= tanα
公式二
设P1(x,y),由点P1与P2关于原点对称,得P2(-x,-y)
把α看成锐角时的符号
函数名不变,符号看象限
课堂练习
利用公式求下列三角函数值
探究新知
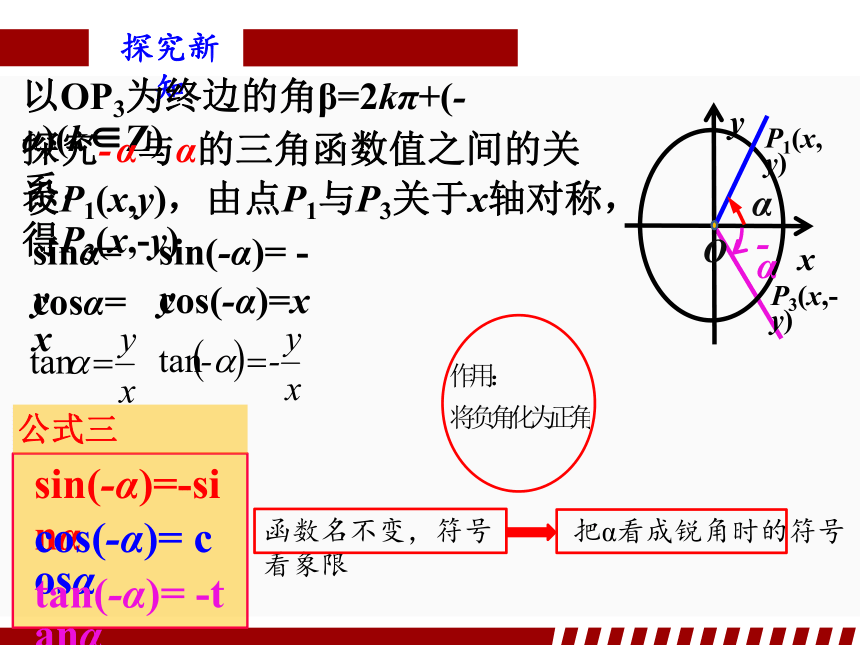
以OP3为终边的角β=2kπ+(-α)(k∈Z)
sinα=y
cosα=x
设P1(x,y),由点P1与P3关于x轴对称,得P3(x,-y)
sin(-α)= -y
cos(-α)=x
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)= -tanα
公式三
P1(x,y)
O
x
α
y
P3(x,-y)
-α
探究- α与α的三角函数值之间的关系,
把α看成锐角时的符号
函数名不变,符号看象限
探究新知
以OP4为终边的角β=2kπ+(π-α)(k∈Z)
sinα=y
cosα=x
P1(x,y)与P4(-x,y)关于y轴对称
sin(π-α)=y
cos(π-α)= -x
sin(π-α)=sinα
cos(π-α)=- cosα
tan(π-α)= -tanα
公式四
P1(x,y)
O
x
α
y
P4(-x,y)
π-α
把α看成锐角时的符号
函数名不变,符号看象限
课堂练习
利用公式求下列三角函数值
探究新知
sin(α+2kπ)=sinα
cos(α+2kπ)=cosα
tan(α+2kπ)=tanα
公式一
sin(π+α)=-sinα
cos(π+α)= -cosα
tan(π+α)= tanα
公式二
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)= -tanα
公式三
sin(π-α)=sinα
cos(π-α)=- cosα
tan(π-α)= -tanα
公式四
诱导公式
(公式一~公式四)
简记:
函数名不变,符号看象限.
例题讲解
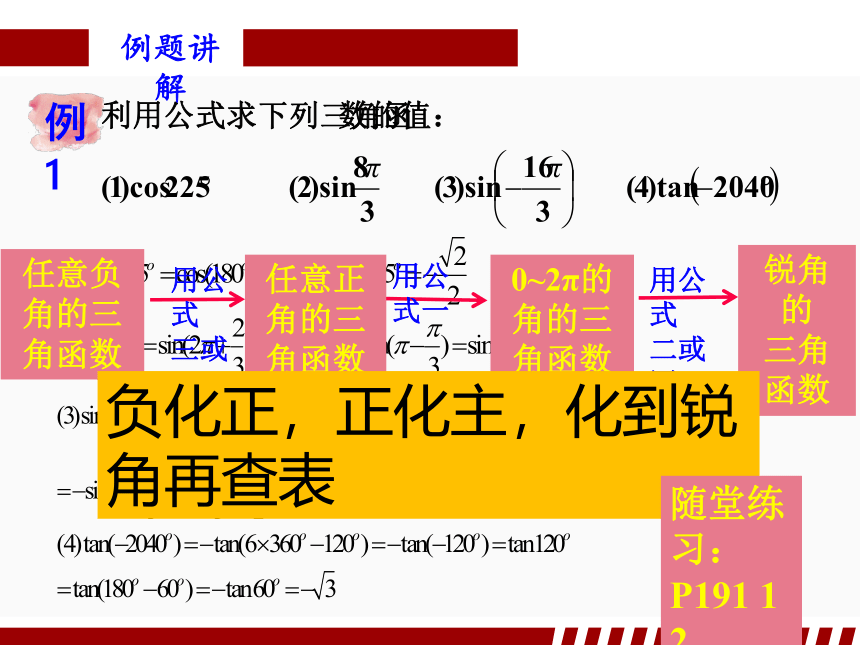
例1
任意负角的三角函数
任意正角的三角函数
0~2π的角的三角函数
锐角的
三角函数
用公式
三或一
用公式一
用公式
二或四
负化正,正化主,化到锐角再查表
随堂练习:
P191 1 2
例题讲解
例2
随堂练习:
P191 3
例题讲解
例2.已知,且为第四象限角,求的值.
解:∵,且为第四象限角,
∴.
∴
探究新知
P1(x-,y)
O
x
α
y
P5(x5,y5)
y=x
问题5:作P1关于直线y=x对称点P5,以OP5为终边的角γ与角α有什么关系?角γ,α的三角函数值之间有什么关系?
sinα=y
cosα=x
x5=y , y5= x
公式五
因为P1(x,y)与P5(x5,y5)关于直线y=x对称
以OP5为终边的角
探究新知
问题6:分别作P5关于y轴、原点、x轴的对称点P6、P7、P8,你有什么新的结论?
P1(x,y)
O
x
α
y
P5(y,x)
y=x
P1(x,y)
O
x
α
y
P5(x5,y5)
P6(x6,y6)
O
P1(x,y)
x
α
y
P5(x5,y5)
P7(x7,y7)
O
P1(x,y)
x
α
y
P5(x5,y5)
P8(x8,y8)
探究新知
P1(x,y)
O
x
α
y
P5(y,x)
P6(x6,y6)
sinα=y
cosα=x
x6=-y , y6= x
公式六
因为P5(y,x)与P6(x6,y6)关于y轴对称
问题7
π/2+α的终边与α的终边有怎样的对称性?
以OP6为终边的角
α的终边先关于直线y=x对称,再关于y轴对称就得到 +α的终边
探究新知
sinα=y
cosα=x
x7=-y , y7=-x
公式七
P5(y,x)与P7(x7,y7)关于原点对称
以OP7为终边的角
问题8
3π/2-α的终边与α的终边有怎样的对称性?
α的终边先关于直线y=x对称,再关于原点对称就得到3π/2-α的终边
O
P1(x,y)
x
α
y
P5(y,x)
P7(x7,y7)
探究新知
sinα=y
cosα=x
x8=y , y8= -x
公式八
P5(y,x)与P8(x8,y8)关于x轴对称
以OP8为终边的角
问题9
3π/2+α的终边与α的终边有怎样的对称性?
α的终边先关于直线y=x对称,再关于x轴对称就得到3π/2+α的终边
O
P1(x,y)
x
α
y
P5(y,x)
P8(x8,y8)
探究新知
诱导公式总结:
口诀:奇变偶不变,符号看象限
意义:
探究新知
公式三:
公式一:
公式四:
公式二:
奇变偶不变,符号看象限.
公式五:
公式六:
公式七:
公式八:
例题讲解
例3
课堂练习
1.sin21°+sin22°+sin23°+…+sin289°.
探究新知
例题讲解
例题讲解
例题讲解
例题讲解
例题讲解
题型一:利用诱导公式化简求值
例1.若那么的值为().
A. B.- C. D.
解:∵
∴
故选A.
例题讲解
题型一:利用诱导公式化简求值
例题讲解
例题讲解
1.求值问题中角的转化方法:
任意负角的三角函数
任意正角的三角函数
0的角的三角函数
锐角的三角函数
公式
一或三
公式
一
公式二或
五或六
2.用诱导公式进行化简的要求:
三角函数的化简是表达式经过某种变形使结果尽可能的简单:
(1)化简后项数尽可能的少.
(2)函数的种类尽可能的少.
(3)分母不含三角函数的符号.
(4)能求值的一定要求值.
(5)含有较高次数的三角函数式,多用因式分解、约分等.
例题讲解
题型二:利用诱导公式证明恒等式
例2.已知求证:
证明:由,得
则原式左边
右边.
所以原等式成立.
例题讲解
证明等式的常见方法:
利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消失差异.
例题讲解
题型三:诱导公式的综合应用
例3.在平面直角坐标系中,角的顶点与坐标原点重合,始边为轴的非负半轴,终边分别与单位圆交于A,B两点,A,B两点的纵坐标分别为
(1)求的值;
解:(1)∵的终边与单位圆交于点B,B点的纵坐标为,∴
∵∴
∴
例题讲解
例3.在平面直角坐标系中,角的顶点与坐标原点重合,始边为轴的非负半轴,终边分别与单位圆交于A,B两点,A,B两点的纵坐标分别为
(2)求的值.
解:(2)∵的终边与单位圆交于点A,A点的纵坐标为,∴
∵∴
故
例题讲解
变3.已知是方程的根,是第三象限角,
求的值.
解:方程的两根为,
∵∴
又是第三象限角,
∴
∴
例题讲解
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子、分母同乘一个式子变形.
例题讲解
题型三:诱导公式的综合应用—在三角形中的应用
例题讲解
例题讲解
例题讲解
课堂练习
又B,C为△ABC的内角,所以C=B,
解 因为A+B+C=π,所以A+B-C=π-2C,A-B+C=π-2B.
所以△ABC为等腰三角形.
课堂小结
①三角函数的简化过程图:
任意负角的
三角函数
任意正角的
三角函数
三角函数
的
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四或五或六
②三角函数的简化过程口诀:负化正,正化小,化到锐角为终了.
符号看象限
奇变偶不变,
③诱导公式记忆口诀:
布置作业
(1)教材
(2)同步作业
5.3 诱导公式
第五章 三角函数
引 入
问题1:三角函数的定义?
问题2:由三角函数定义,我们得到了公式一及同角三角函数的基本关系,它的研究思路是什么?
sin(α+2kπ)=sinα
cos(α+2kπ)=cosα
tan(α+2kπ)=tanα
公式一
k∈Z
研究思路:利用单位圆,从角的数量关系→坐标间的关系→三角函数函数值的关系得到了公式(一).
引 入
α∈(0°,90°)
180°+α∈(180°,270°)
180°-α∈(90°,180°)
360°-α∈(270°,360°)
问题3:能否再把0°~ 360°间的角的三角函数求值,化为我们熟悉的00~900间的角的三角函数求值问题呢?
圆的最重要的性质是对称性,而对称性(如奇偶性)也是函数的重要性质.由此想到,可以利用圆的对称性,研究三角函数的对称性.
探究新知
P1(x1,y1)
O
x
α
y
P4(x4,y4)
P1(x1,y1)
O
x
α
y
P3(x3,y3)
问题4:(1)作P1关于原点的对称点P2,以OP2为终边的角β与角α有什么关系?角β,α的三角函数值之间有什么关系?
(2)作P1关于x轴的对称点P3,有什么结论?
(3)作P1关于y轴的对称点P4,有什么结论?
180°+α∈(180°,270°)
P1(x1,y1)
O
x
α
y
P2(x2,y2)
360°-α∈(270°,360°)
-α
180°-α∈(90°,180°)
探究新知
P1(x,y)
O
x
α
y
P2(-x,-y)
π+α
以OP2为终边的角β=2kπ+(π+α)(k∈Z)
sinα=y
cosα=x
探究π+α与α的三角函数值之间的关系,
sin(π+α)= -y
cos(π+α)= -x
sin(π+α)=-sinα
cos(π+α)= -cosα
tan(π+α)= tanα
公式二
设P1(x,y),由点P1与P2关于原点对称,得P2(-x,-y)
把α看成锐角时的符号
函数名不变,符号看象限
课堂练习
利用公式求下列三角函数值
探究新知
以OP3为终边的角β=2kπ+(-α)(k∈Z)
sinα=y
cosα=x
设P1(x,y),由点P1与P3关于x轴对称,得P3(x,-y)
sin(-α)= -y
cos(-α)=x
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)= -tanα
公式三
P1(x,y)
O
x
α
y
P3(x,-y)
-α
探究- α与α的三角函数值之间的关系,
把α看成锐角时的符号
函数名不变,符号看象限
探究新知
以OP4为终边的角β=2kπ+(π-α)(k∈Z)
sinα=y
cosα=x
P1(x,y)与P4(-x,y)关于y轴对称
sin(π-α)=y
cos(π-α)= -x
sin(π-α)=sinα
cos(π-α)=- cosα
tan(π-α)= -tanα
公式四
P1(x,y)
O
x
α
y
P4(-x,y)
π-α
把α看成锐角时的符号
函数名不变,符号看象限
课堂练习
利用公式求下列三角函数值
探究新知
sin(α+2kπ)=sinα
cos(α+2kπ)=cosα
tan(α+2kπ)=tanα
公式一
sin(π+α)=-sinα
cos(π+α)= -cosα
tan(π+α)= tanα
公式二
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)= -tanα
公式三
sin(π-α)=sinα
cos(π-α)=- cosα
tan(π-α)= -tanα
公式四
诱导公式
(公式一~公式四)
简记:
函数名不变,符号看象限.
例题讲解
例1
任意负角的三角函数
任意正角的三角函数
0~2π的角的三角函数
锐角的
三角函数
用公式
三或一
用公式一
用公式
二或四
负化正,正化主,化到锐角再查表
随堂练习:
P191 1 2
例题讲解
例2
随堂练习:
P191 3
例题讲解
例2.已知,且为第四象限角,求的值.
解:∵,且为第四象限角,
∴.
∴
探究新知
P1(x-,y)
O
x
α
y
P5(x5,y5)
y=x
问题5:作P1关于直线y=x对称点P5,以OP5为终边的角γ与角α有什么关系?角γ,α的三角函数值之间有什么关系?
sinα=y
cosα=x
x5=y , y5= x
公式五
因为P1(x,y)与P5(x5,y5)关于直线y=x对称
以OP5为终边的角
探究新知
问题6:分别作P5关于y轴、原点、x轴的对称点P6、P7、P8,你有什么新的结论?
P1(x,y)
O
x
α
y
P5(y,x)
y=x
P1(x,y)
O
x
α
y
P5(x5,y5)
P6(x6,y6)
O
P1(x,y)
x
α
y
P5(x5,y5)
P7(x7,y7)
O
P1(x,y)
x
α
y
P5(x5,y5)
P8(x8,y8)
探究新知
P1(x,y)
O
x
α
y
P5(y,x)
P6(x6,y6)
sinα=y
cosα=x
x6=-y , y6= x
公式六
因为P5(y,x)与P6(x6,y6)关于y轴对称
问题7
π/2+α的终边与α的终边有怎样的对称性?
以OP6为终边的角
α的终边先关于直线y=x对称,再关于y轴对称就得到 +α的终边
探究新知
sinα=y
cosα=x
x7=-y , y7=-x
公式七
P5(y,x)与P7(x7,y7)关于原点对称
以OP7为终边的角
问题8
3π/2-α的终边与α的终边有怎样的对称性?
α的终边先关于直线y=x对称,再关于原点对称就得到3π/2-α的终边
O
P1(x,y)
x
α
y
P5(y,x)
P7(x7,y7)
探究新知
sinα=y
cosα=x
x8=y , y8= -x
公式八
P5(y,x)与P8(x8,y8)关于x轴对称
以OP8为终边的角
问题9
3π/2+α的终边与α的终边有怎样的对称性?
α的终边先关于直线y=x对称,再关于x轴对称就得到3π/2+α的终边
O
P1(x,y)
x
α
y
P5(y,x)
P8(x8,y8)
探究新知
诱导公式总结:
口诀:奇变偶不变,符号看象限
意义:
探究新知
公式三:
公式一:
公式四:
公式二:
奇变偶不变,符号看象限.
公式五:
公式六:
公式七:
公式八:
例题讲解
例3
课堂练习
1.sin21°+sin22°+sin23°+…+sin289°.
探究新知
例题讲解
例题讲解
例题讲解
例题讲解
例题讲解
题型一:利用诱导公式化简求值
例1.若那么的值为().
A. B.- C. D.
解:∵
∴
故选A.
例题讲解
题型一:利用诱导公式化简求值
例题讲解
例题讲解
1.求值问题中角的转化方法:
任意负角的三角函数
任意正角的三角函数
0的角的三角函数
锐角的三角函数
公式
一或三
公式
一
公式二或
五或六
2.用诱导公式进行化简的要求:
三角函数的化简是表达式经过某种变形使结果尽可能的简单:
(1)化简后项数尽可能的少.
(2)函数的种类尽可能的少.
(3)分母不含三角函数的符号.
(4)能求值的一定要求值.
(5)含有较高次数的三角函数式,多用因式分解、约分等.
例题讲解
题型二:利用诱导公式证明恒等式
例2.已知求证:
证明:由,得
则原式左边
右边.
所以原等式成立.
例题讲解
证明等式的常见方法:
利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消失差异.
例题讲解
题型三:诱导公式的综合应用
例3.在平面直角坐标系中,角的顶点与坐标原点重合,始边为轴的非负半轴,终边分别与单位圆交于A,B两点,A,B两点的纵坐标分别为
(1)求的值;
解:(1)∵的终边与单位圆交于点B,B点的纵坐标为,∴
∵∴
∴
例题讲解
例3.在平面直角坐标系中,角的顶点与坐标原点重合,始边为轴的非负半轴,终边分别与单位圆交于A,B两点,A,B两点的纵坐标分别为
(2)求的值.
解:(2)∵的终边与单位圆交于点A,A点的纵坐标为,∴
∵∴
故
例题讲解
变3.已知是方程的根,是第三象限角,
求的值.
解:方程的两根为,
∵∴
又是第三象限角,
∴
∴
例题讲解
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子、分母同乘一个式子变形.
例题讲解
题型三:诱导公式的综合应用—在三角形中的应用
例题讲解
例题讲解
例题讲解
课堂练习
又B,C为△ABC的内角,所以C=B,
解 因为A+B+C=π,所以A+B-C=π-2C,A-B+C=π-2B.
所以△ABC为等腰三角形.
课堂小结
①三角函数的简化过程图:
任意负角的
三角函数
任意正角的
三角函数
三角函数
的
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四或五或六
②三角函数的简化过程口诀:负化正,正化小,化到锐角为终了.
符号看象限
奇变偶不变,
③诱导公式记忆口诀:
布置作业
(1)教材
(2)同步作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
