第六章 反比例函数单元复习题（含答案）

中小学教育资源及组卷应用平台
北师大版九年级数学第六章《反比例函数》单元复习练习题（含答案）
一、单选题
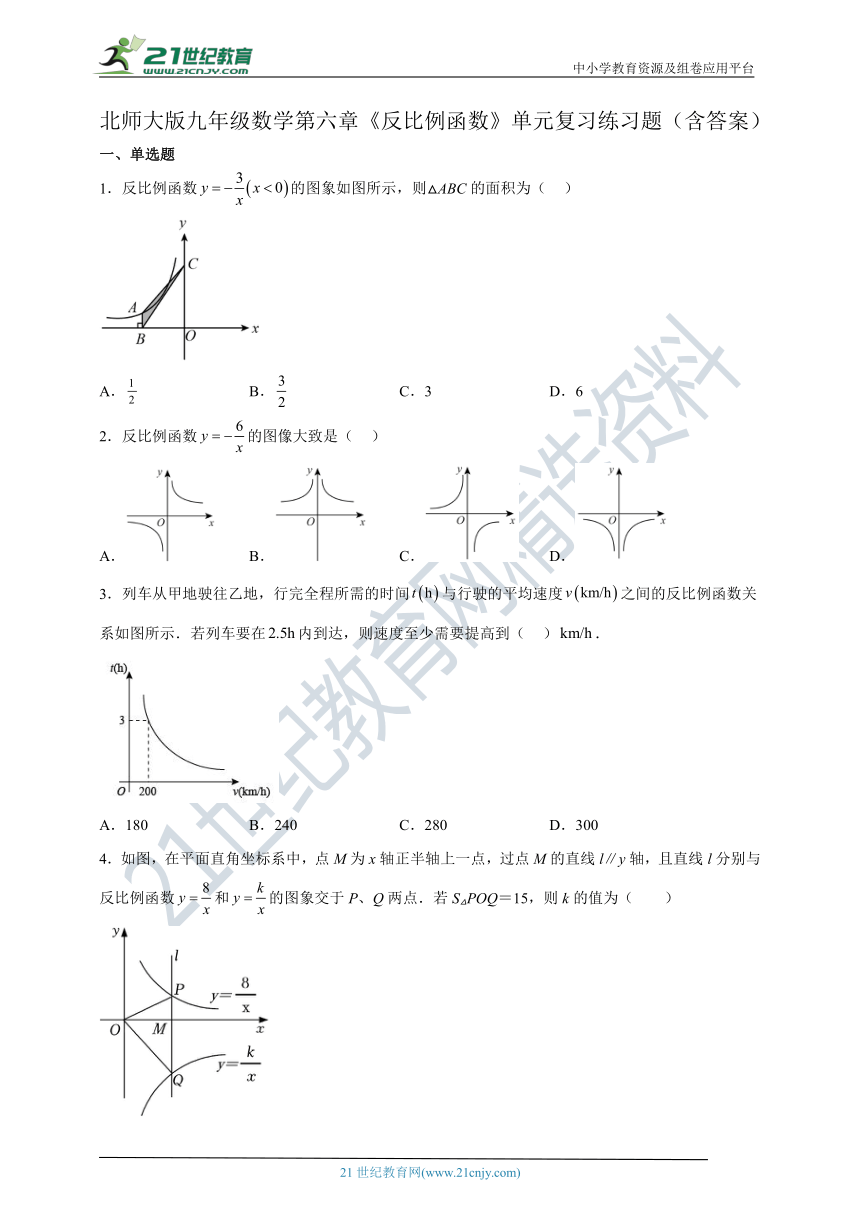
1．反比例函数的图象如图所示，则△ABC的面积为（ ）
A． B． C．3 D．6
2．反比例函数的图像大致是（ ）
A． B． C． D．
3．列车从甲地驶往乙地，行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示．若列车要在内到达，则速度至少需要提高到（ ）．
A．180 B．240 C．280 D．300
4．如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l∥y轴，且直线l分别与反比例函数和的图象交于P、Q两点．若S△POQ＝15，则k的值为（　　）
A．38 B．22 C．﹣7 D．﹣22
5．关于函数，下列说法中正确的是（ ）
A．图像位于第一、三象限 B．图像与坐标轴没有交点
C．图像是一条直线 D．y的值随x的值增大而减小
6．某城市市区人口万人，市区绿地面积50万平方米，平均每人拥有绿地平方米，则与之间的函数表达式为（ ）
A． B． C． D．
7．如图，一次函数、为常数，与反比例函数的图象交于A（1，m），B（n，2）两点，与坐标轴分别交于，两点．则△AOB的面积为( )
A．3 B．6 C．8 D．12
8．已知反比例函数y=（k≠0），且在各自象限内，y随x的增大而增大，则下列点可能在这个函数图象上的为（ ）
A．（2，3） B．（-2，3） C．（3，0） D．（-3，0）
9．对于反比例函数y＝﹣，下列说法错误的是（　　）
A．图象经过点（1，﹣5）
B．图象位于第二、第四象限
C．当x＜0时，y随x的增大而减小
D．当x＞0时，y随x的增大而增大
10．若反比例函数的图象经过点，则它的图象也一定经过的点是（ ）
A． B． C． D．
11．某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值）与该校参加竞赛人数的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（ ）
A．甲 B．乙 C．丙 D．丁
12．如图，在平面直角坐标系中，直线y＝x与反比例函数y＝（x＞0）的图象交于点A，将直线y＝x沿y轴向上平移b个单位长度，交y轴于点B，交反比例函数图象于点C．若OA＝2BC，则b的值为（　　）
A．1 B．2 C．3 D．4
二、填空题
13．若、两点都在函数的图像上，且<，则k的取值范围是______．
14．已知点在双曲线上，点在直线上，则的值为______．
15．如图所示，矩形顶点、在轴上，顶点在第一象限，轴为该矩形的一条对称轴，且矩形的面积为6．若反比例函数的图象经过点，则的值为_________．
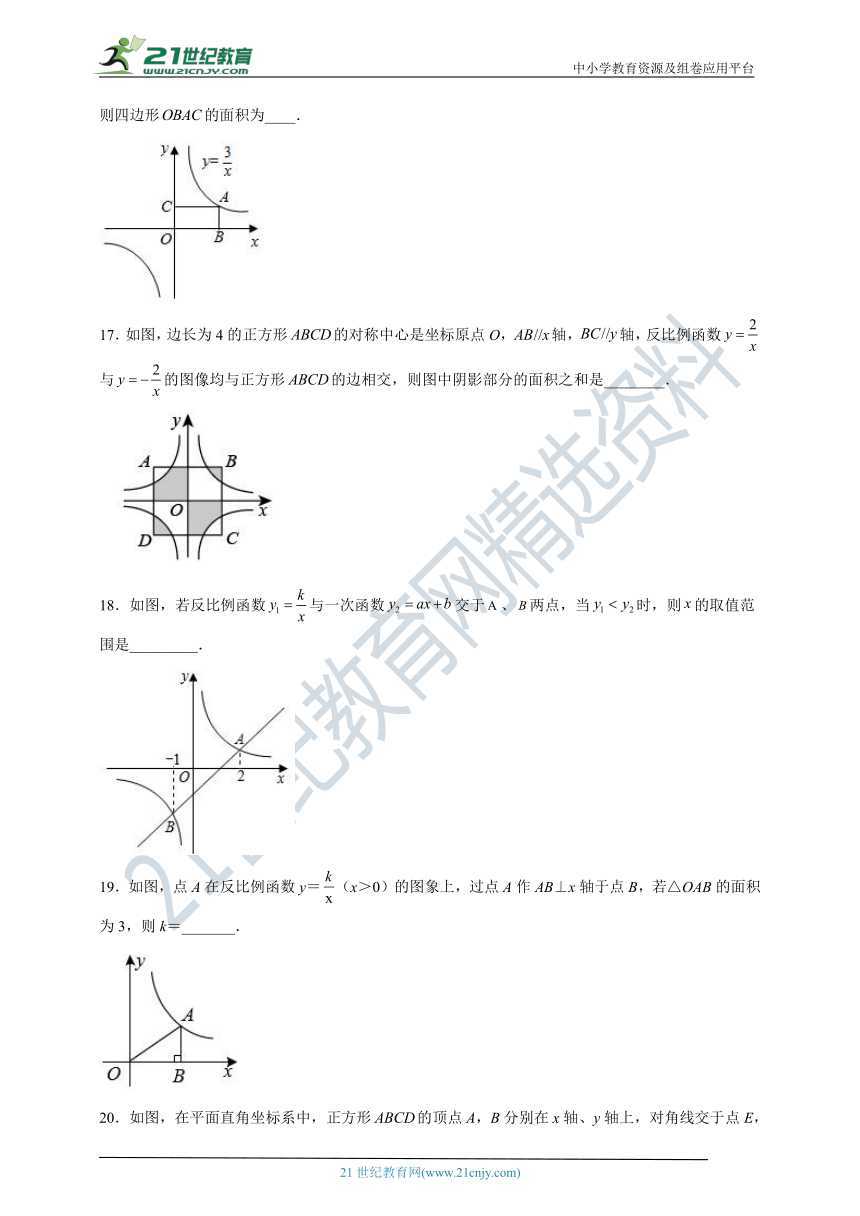
16．如图，点是反比例函数图象上任意一点，过点分别作轴，轴的垂线，垂足为，，则四边形的面积为____．
17．如图，边长为4的正方形的对称中心是坐标原点O，轴，轴，反比例函数与的图像均与正方形的边相交，则图中阴影部分的面积之和是________．
18．如图，若反比例函数与一次函数交于、两点，当时，则的取值范围是_________．
19．如图，点A在反比例函数y＝（x＞0）的图象上，过点A作AB⊥x轴于点B，若△OAB的面积为3，则k＝_______．
20．如图，在平面直角坐标系中，正方形的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数的图像经过点C，E．若点，则k的值是_________．
三、解答题
21．如图，在平面直角坐标系中，反比例函数y（x＞0）的图象经过点A（2，6），将点A向右平移2个单位，再向下平移a个单位得到点B，点B恰好落在反比例函数y（x＞0）的图象上，过A，B两点的直线与y轴交于点C．
（1）求k的值及点C的坐标；
（2）在y轴上有一点D（0，5），连接AD，BD，求△ABD的面积．
22．如图，在平面直角坐标系中，O为坐标原点，Rt△OAB的直角边OB在x轴的正半轴上，点A的坐标为（6，4），斜边OA的中点D在反比例函数y（x＞0）的图象上，AB交该图象于点C，连接OC．
(1)求k的值；
(2)求△OAC的面积．
23．如图是反比例函数y＝的图象的一支．根据图象解决下列问题：
(1)求m的取值范围；
(2)若点A（m-3，b1）和点B（m-4，b2）是该反比例函数图象上的两点，请你判断b1与b2的大小关系，并说明理由．
24．教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后接通电源，则自动开始加热，每分钟水温上升10℃，待加热到100℃，饮水机自动停止加热，水温开始下降．水温y（℃）和通电时间x（min）成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20℃，接通电源后，水温y（℃）和通电时间x（min）之间的关系如图所示，回答下列问题：
(1)分别求出当0≤x≤8和8＜x≤a时，y和x之间的函数关系式；
(2)求出图中a的值；
(3)李老师这天早上7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40℃的开水，则他需要在什么时间段内接水？
25．如图，A（4，3）是反比例函数y=在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．
（1）求反比例函数y=的表达式；
（2）求点B的坐标；
（3）求△OAP的面积．
26．如图，一次函数与反比例函数的图象交于，两点．
（1）求反比例函数的解析式和的值；
（2）根据图象直接写出不等式的的取值范围；
（3）求的面积．
27．如图，已知一次函数与反比例函数的图象在第一、三象限分别交于，两点，连接，．
（1）求一次函数和反比例函数的解析式；
（2）的面积为______；
（3）直接写出时x的取值范围．
28．如图，一次函数的图象与反比例函数（为常数且）的图象相交于，两点．
（1）求反比例函数的表达式；
（2）将一次函数的图象沿轴向下平移个单位，使平移后的图象与反比例函数的图象有且只有一个交点，求的值．
29．如图，一次函数的图像与反比例函数(k＞0)的图像交于A，B两点，过点A做x轴的垂线，垂足为M，△AOM面积为1.
（1）求反比例函数的解析式；
（2）在y轴上求一点P,使PA+PB的值最小，并求出其最小值和P点坐标.
参考答案
1．B2．C3．B4．D5．B6．C7．A8．B9．C10．C11．C12．C
13．k<0
14．-3
15．3
16．3
17．8
18．
19．6
20．4
21．解：（1）把点代入，，
反比例函数的解析式为，
将点向右平移2个单位，
，
当时，，
，
设直线的解析式为，
由题意可得，
解得，
，
当时，，
；
（2）由（1）知，
．
22．（1）解：点的坐标为，点为的中点，
点的坐标为，
点在反比例函数的图象上，
；
（2）
解：由题意得，点的横坐标为6，
点的纵坐标为：，
，
的面积．
23．（1）
解：由图象可知，，
解得，
∴的取值范围为．
（2）
解：．
理由如下：∵，
∴，
由反比例函数的图象与性质可知，当时，随着的增大而减小，
∴．
24．（1）
当0≤x≤8时，设y＝k1x+b，
将（0，20），（8，100）的坐标分别代入y＝k1x+b得，
解得k1＝10，b＝20．
∴当0≤x≤8时，y＝10x+20．
当8＜x≤a时，设y＝，
将（8，100）的坐标代入y＝，
得k2＝800
∴当8＜x≤a时，y＝．
综上，当0≤x≤8时，y＝10x+20；当8＜x≤a时，y＝．
（2）
将y＝20代入y＝，
解得x＝40，
即a＝40；
（3）
当y＝40时，x＝＝20．
∴要想喝到不低于40℃的开水，x需满足8≤x≤20，
即李老师要在7：38到7：50之间接水．
25．（1）将点A（4，3）代入y=，得：k=12，
则反比例函数解析式为y=；
（2）如图，过点A作AC⊥x轴于点C，
则OC=4、AC=3，
∴OA==5，
∵AB∥x轴，且AB=OA=5，
∴点B的坐标为（9，3）；
（3）∵点B坐标为（9，3），
∴OB所在直线解析式为y=x，
由可得点P坐标为（6，2），（负值舍去），
过点P作PD⊥x轴，延长DP交AB于点E，
则点E坐标为（6，3），
∴AE=2、PE=1、PD=2，
则△OAP的面积=×（2+6）×3﹣×6×2﹣×2×1=5．
26．解：（1）在的图象上，
，
反比例函数的解析式是．
又∵在的图象上，
；
（2）由图像可知：当或时，；
（3），在函数的图象上，
，
解得：，
则一次函数的解析式是，
设直线与轴相交于点，则的坐标是．
∴
．
27．解：（1）把代入反比例函数得：
m=6，
∴反比例函数的解析式为，
∵点在反比例函数图像上，
∴-3a=6，解得a=-2，
∴B（-2，-3），
∵一次函数y1=kx+b的图象经过A和B，
∴，解得：，
∴一次函数的解析式为；
（2）∵，，一次函数的解析式为，
令y=0，解得：x=4，即一次函数图像与x轴交点为（4，0），
∴S△AOB=，
故答案为：8；
（3）由图象可知：
时，即一次函数图像在反比例函数图像上方，
x的取值范围是：-2＜x＜0或x＞6.
28．（1）由题意，将点代入一次函数得：
将点代入得：，解得
则反比例函数的表达式为；
（2）将一次函数的图象沿轴向下平移个单位得到的一次函数的解析式为
联立
整理得：
一次函数的图象与反比例函数的图象有且只有一个交点
关于x的一元二次方程只有一个实数根
此方程的根的判别式
解得
则b的值为1或9．
29．（1）反比例函数的图象过点，过点作轴的垂线，垂足为，面积为1，
，
，
，
故反比例函数的解析式为：；
（2）作点关于轴的对称点，连接，交轴于点，则最小．
由，解得，或，
，，
，最小值．
设直线的解析式为，
则，解得，
直线的解析式为，
时，，
点坐标为．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)