人教版数学八上 11.1.3三角形的稳定性 学案(无答案)
文档属性
| 名称 | 人教版数学八上 11.1.3三角形的稳定性 学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 08:23:51 | ||
图片预览

文档简介
11.1.3 三角形的稳定性
学习目标:
1.认识三角形并会用几何语言表示三角形,了解三角
形分类.
2.掌握三角形的三边关系.(难点)
3.运用三角形三边关系解决有关的问题.(重点)
学习过程:
一、要点探究
探究点1:三角形的稳定性
活动1:
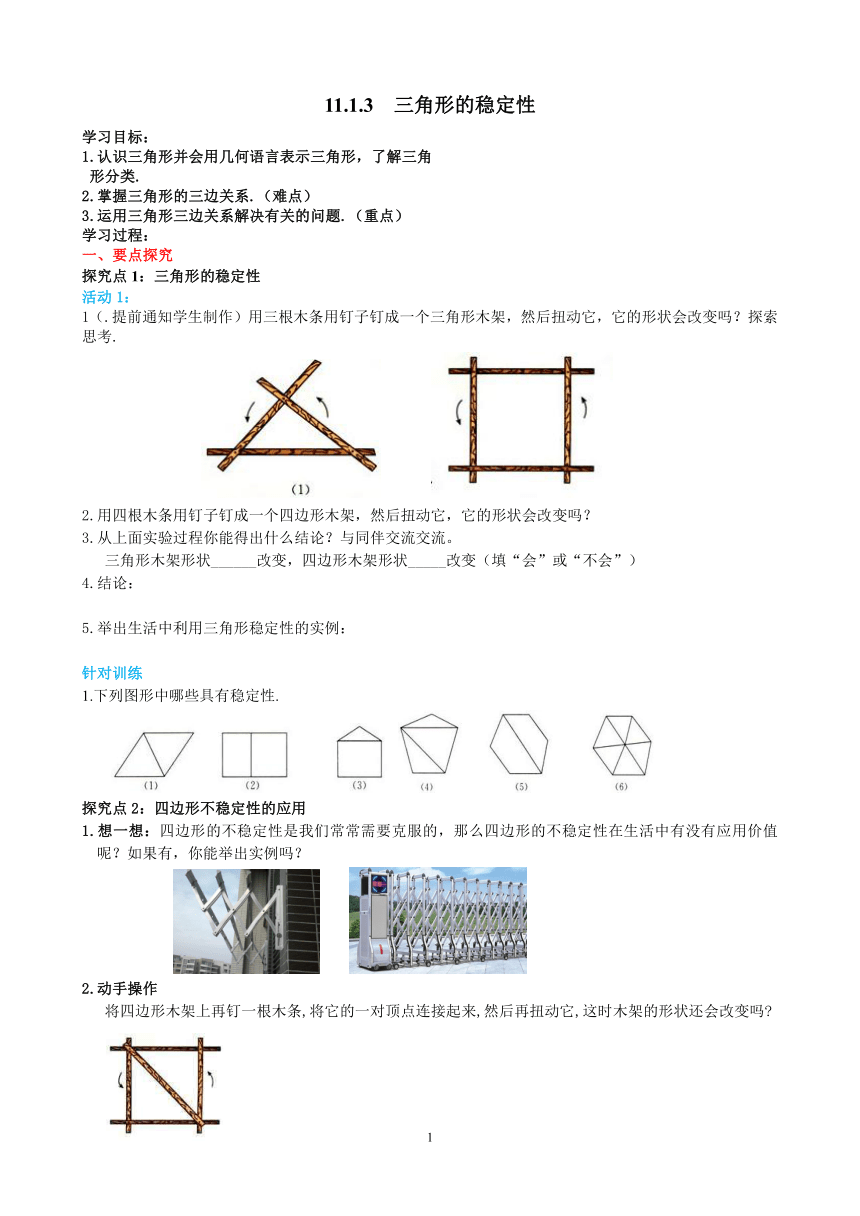
1(.提前通知学生制作)用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?探索思考.
2.用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3.从上面实验过程你能得出什么结论?与同伴交流交流。
三角形木架形状______改变,四边形木架形状_____改变(填“会”或“不会”)
4.结论:
5.举出生活中利用三角形稳定性的实例:
针对训练
1.下列图形中哪些具有稳定性.
探究点2:四边形不稳定性的应用
1.想一想:四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
2.动手操作
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗
例1:要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使五边形,六边形木架,七边形木架保持稳定该怎么办呢
帮帮忙:1.牧民阿其木家用于圈羊的木栅门,由于年久失修已经变成如图甲,为什么会变
形?
2.为了恢复成原样图乙,而且要保持形状不变,他该怎么做呢?
二、课堂小结:
三角形具有稳定性,四边形没有稳定性。它们都有一定的实用价值。
三、课堂练习
1.下列关于三角形稳定性和四边形不稳定性的说法正确的是 ( )
A.稳定性总是有益的,而不稳定性总是有害的
B.稳定性有利用价值,而不稳定性没有利用价值
C.稳定性和不稳定性均有利用价值
D.以上说法都不对
2.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.三角形的稳定性
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短 B.三角形具有稳定性
C.长方形是轴对称图形 D.长方形的四个角都是直角
4.桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的 ___________性.
5.人站在晃动的公共汽车上.若你分开两腿站立,则需伸出一只手去抓栏杆才能站稳,这是利用了 .
6如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
拓展:要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使n边形木架保持稳定该钉几根木条呢
学习目标:
1.认识三角形并会用几何语言表示三角形,了解三角
形分类.
2.掌握三角形的三边关系.(难点)
3.运用三角形三边关系解决有关的问题.(重点)
学习过程:
一、要点探究
探究点1:三角形的稳定性
活动1:
1(.提前通知学生制作)用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?探索思考.
2.用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3.从上面实验过程你能得出什么结论?与同伴交流交流。
三角形木架形状______改变,四边形木架形状_____改变(填“会”或“不会”)
4.结论:
5.举出生活中利用三角形稳定性的实例:
针对训练
1.下列图形中哪些具有稳定性.
探究点2:四边形不稳定性的应用
1.想一想:四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
2.动手操作
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗
例1:要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使五边形,六边形木架,七边形木架保持稳定该怎么办呢
帮帮忙:1.牧民阿其木家用于圈羊的木栅门,由于年久失修已经变成如图甲,为什么会变
形?
2.为了恢复成原样图乙,而且要保持形状不变,他该怎么做呢?
二、课堂小结:
三角形具有稳定性,四边形没有稳定性。它们都有一定的实用价值。
三、课堂练习
1.下列关于三角形稳定性和四边形不稳定性的说法正确的是 ( )
A.稳定性总是有益的,而不稳定性总是有害的
B.稳定性有利用价值,而不稳定性没有利用价值
C.稳定性和不稳定性均有利用价值
D.以上说法都不对
2.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.三角形的稳定性
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短 B.三角形具有稳定性
C.长方形是轴对称图形 D.长方形的四个角都是直角
4.桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的 ___________性.
5.人站在晃动的公共汽车上.若你分开两腿站立,则需伸出一只手去抓栏杆才能站稳,这是利用了 .
6如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
拓展:要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使n边形木架保持稳定该钉几根木条呢
